Компьютерное дополнение к курсу Информатика 6. 2024

Урок 34. «Повторение»

Задача 241. Эта задача аналогична задаче 46. Решается она стандартным способом – построением дерева перебора всех подмножеств.

Задача 242. Если кто-то из ребят ошибется при построении последовательности, скорее всего, он забыл, что такое среднее арифметическое чисел. Таким детям придется напомнить, что это такое. В данном случае последовательность задана общим правилом, связывающим каждый член последовательности с двумя соседями – следующим и предыдущим (рекуррентное задание последовательности). Поэтому данную последовательность можно строить только с начала – с первого члена. Итак, первый член равен числу 3, второй – числу 7. Из последнего утверждения следует, что второй член равен среднему арифметическому первого и третьего членов (в данном случае просто их полусумме). Получаем уравнение: (3 + х) : 2 = 7, отсюда х =11. Итак, третий член последовательности равен 11. Аналогично находим четвертый и пятый члены. Заметим, что построенная последовательность – арифметическая прогрессия, ведь третье утверждение является необходимым и достаточным условием построения арифметической прогрессии.

Ответ: 3–7–11–15–19.

Задача 243. Необязательная. Это очень полезная для детей задача. Она имеет обобщающий характер и использует дополнительную информацию, которую детям сначала нужно найти в рамках нашего учебника. Это задача на сортировку объектов, критерием сортировки слов является принадлежность входящих в них букв к некоторому языку, которая устанавливается с помощью сравнения букв с буквами-образцами, которые приведены в других задачах учебника. Грузинские буквы ребята смогут найти в задаче 177, армянские – в задаче 104, греческие – в задаче 81. Заметим, что буквы в разных задачах нашего учебника немного по-разному стилизованы, что, в общем, характерно для любого живого языка, ведь даже почерк у разных людей может различаться очень сильно. Поэтому дети в этой задаче могут использовать не только формальное сравнение букв, но и общие отличительные признаки написания букв. Буквы греческого алфавита могут быть знакомы ребятам по урокам математики, например буква π.

Ответ: грузинские слова: 6, 11, 14, армянские слова: 1, 5, 8, 12, греческие слова: 2, 4, 9, 13, еврейские слова: 3, 7, 10.

Задача 244. Строить дерево по набору его последовательностей детям уже приходилось. Однако, если нет никаких дополнительных условий, сделать это можно по-разному. Можно, например, пустить каждое слово в виде отдельной последовательности. В таком дереве каждый родитель будет иметь ровно одного ребенка, поэтому элементов в дереве будет ровно столько, сколько всего элементов во всех последовательностях. В данном случае такой способ явно не годится, ведь в словах всего 45 букв, а в дереве должно быть 23 элемента. Значит, элементы нужно «экономить»: не рисовать одинаковые элементы на одном уровне, если их можно заменить одним элементом. Например, у всех последовательностей дерева одинаковая первая буква – Д, значит, сделаем в дереве А один элемент первого уровня – букву Д. 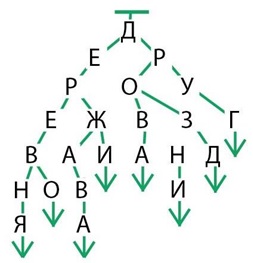Вторые буквы в словах – либо Е, либо Р, значит, у буквы Д будет двое детей – Е и Р. Так будем «экономить» и дальше, в результате как раз получим дерево, в котором ровно 23 элемента:

Задача 245. Простая задача, которую можно предлагать даже слабым учащимся. Решать задачу можно по-разному. Например, сначала строить последовательность по возрастанию, прибавляя семерку к каждому следующему члену. Можно строить и с конца, отнимая семерку от каждого следующего члена. Но сначала надо найти максимальное двузначное число, делящееся на 7. Это 98.

Задача 246. Как видите, задача объемная, но содержательно не слишком сложная. Удобнее всего решать ее, вычеркивая из множества Д все неподходящие числа, анализируя утверждения по порядку.

Ответ: {69, 87, 81, 63, 93}.

Задача 247. Необязательная. Иногда бывает удобно делить все объекты не на две, а на три кучки. Аналогичным образом ситуация складывается и в этой задаче. Разделим все монеты на три кучки и взвесим любые две. Если весы будут в равновесии, значит, фальшивая монета в третьей кучке. Если весы не уравновесятся, то фальшивая монета в более легкой кучке. Итак, за одно взвешивание нам удалось найти кучку из трех монет, в которой находится фальшивая. Вторым шагом будет взвешивание любых двух монет из той кучки, где находится фальшивая монета. Рассуждения здесь будут такими же.

Если монет всего 27, то снова разобьем их на кучки по 3. Таких кучек будет 9. Берем пару кучек и взвешиваем. Если одна кучка перевешивает, то мы нашли кучку с фальшивой монетой. Если весы в равновесии, берем еще одну пару кучек. Таких взвешиваний придется сделать не более 4-х. Если все 4 взвешивания не обнаружили кучку с фальшивой монетой, значит, она в последней кучке. Далее потребуется 1 взвешивание (см. выше). Итого: 5 взвешиваний.

Задача 248. Необязательная. Как и в некоторых других задачах на построение равновесной выигрышной стратегии, характер равновесной стратегии здесь связан с симметрией начальной позиции. Если число лепестков четное, то ромашка является центрально-симметричной фигурой. В такой ситуации для каждого лепестка существует симметричный ему относительно центра, поэтому Второй может повторить любой ход, сделанный Первым. Отсюда вывод: если число лепестков ромашки четное, то выигрышную стратегию имеет Второй. Если число лепестков нечетное, то Первый, оторвав один лепесток, может свести задачу к только что рассмотренной ситуации. Значит, в этом случае выигрышную стратегию имеет Первый.

Задача 249. Возможно, кому-то из ребят придется помогать, поскольку утверждений много и обеспечить их одновременную истинность может оказаться непросто. Элементами нашего дерева могут быть числа 3, 6 и 9. На первом уровне у нас четыре элемента, причем три листа. Все последовательности у нас должны быть разными, значит, все листья первого уровня у нас тоже должны быть разными. Получаем, что на первом уровне у нас 4 элемента – листья 3, 6 и 9 и один элемент, у которого будут дети, например 3. Аналогичные рассуждения мы проводим для каждого уровня. Заметим, что решений в этом задаче несколько, ведь начиная со второго уровня общее число элементов уровня неизвестно (известно только, что листьев должно быть три). Например, на втором уровне может быть один элемент, не являющийся листом, а может быть и три таких элемента.

Задача 250. Повторение алгоритмов для Робота с использованием команды цикл пока. Ясно, что в общем случае Робот должен сначала идти до упора влево, потом до упора вниз, потом до упора влево, и, наконец, до упора вверх. Хотя поля у нас очень похожи, но число клеток в коридорах разное, поэтому здесь можно использовать только команду цикл пока.

Ответ:

Задача 251. Для сообразительных ребят задача окажется довольно легкой. Общее количество участников трех олимпиад – 198. Пусть в одной олимпиаде участвовало Х человек. В двух олимпиадах участвовало в 2 раза меньше, т.е. по количеству «олимпиадомест» это тоже Х. В трех олимпиадах участвовало в 3 раза меньше, чем в одной, т.е. по количеству «олимпиадомест» это тоже Х. Таким образом, разделив 198 на 3, получим число школьников, участвовавших только в одной олимпиаде: 66. Для вычисления двух других групп делим 66 на 2 и на 3, получаем 33 и 22. Всего учеников, участвовавших в олимпиадах по математике, физике и информатике, - 66 + 33 + 22 = 121.

Задача 252. Повторение алгоритмов для Робота. План действий таков. Робот спускается вниз до стены. Движется направо, отыскивая проход. Спускается вниз до упора. Перемещается вправо до упора.

Ответ:

Задача 253. Задача средней сложности на сообразительность. Разделим стопку на две кучки по 4 монеты. Положим на одну чашу весов 4 эталонных монеты, на другую – одну кучку из 4 монет. Если равновесия нет, значит, в этой кучке находится фальшивая монета, в противном случае фальшивая монета находится в другой кучке. Таким образом, мы локализовали фальшивую монету в стопке из 4-х монет. Далее делим эту стопку на 2 кучки по 2 монеты. Берем две эталонные монеты и, как и на первом шаге, сравниваем их по весу с одной кучкой из 2-х монет. В результате находим кучку из двух монет, в которой находится фальшивая. Далее делим эту кучку на две монеты. Берем одну эталонную монету и сравниваем ее по весу с одной из «потенциально фальшивых» монет. Если равновесия нет, фальшивая монета на весах, в противном случае – на столе.

Задача 254. Необязательная. Для детей эта задача может оказаться неожиданной, но идея решения довольно проста. Посчитаем число черных и белых клеток на шахматном поле: 32 белых и 32 черных клетки. В каждой «костяшке домино» одна черная и одна белая клетка, значит, чтобы замостить какую-то часть шахматной доски «костяшками домино», черных и белых клеток в ней должно быть поровну. У нас же вырезаны 2 черные клетки, значит, разбить такую доску на «костяшки домино» невозможно.

Задача 255. Равновесная выигрышная стратегия Первого в этой игре заключается в том, чтобы на первом ходу провести отрезок, который разделит окружность «пополам»: с девятью точками на каждой дуге. Затем каждый ход Второго на одной из дуг Первый будет зеркально повторять на другой дуге.

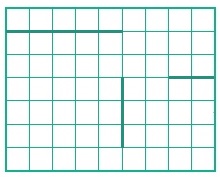
Задача 256. Задачу сильный ученик сможет решить умозрительно. То есть даже без написания программ сможет описать, как должны быть расположены стены. Действительно, Роботу надо сместиться на 6 клеток вниз и на 8 клеток вправо. Алгоритм позволяет шагнуть на 3 клетки вниз, на 3 клетки вправо и на 8 клеток или вниз, или вправо – если нет прохода вниз. Отсюда следует, что с помощью горизонтальной стены мы должны вынудить Робота сместиться вправо на 5 клеток, при этом разрешив спуститься вниз ровно на 3 клетки. Дальше надо проследить, чтобы стены не мешали ему дойти вниз до края поля, а затем – вправо до края поля.

Вот один из возможных вариантов ответа:

Задача 257. Как и в других задачах на перебор вариантов, здесь полезным оказывается дерево перебора. Так как это дерево оказывается слишком большим, лучше не рисовать его, а представить себе, описать, а затем ответить на вопрос задачи. Обозначим людей буквами – А, Б, В, Г, Д, Е, Ж, З. Очередь мы будем строить, конечно, начиная с первого. Тогда первым может быть любой из восьми человек, значит, на первом уровне нашего дерева будет 8 элементов. У каждой из этих элементов 7 детей, ведь вторым может быть любой из оставшихся 7 человек. Значит, на втором уровне 8•7 = 48 элементов. У каждой из этих элементов по 6 детей (48•6 = 288). Так мы описываем дерево вплоть до первого уровня.

Ответ: 8 человек могут встать в очередь 40 320 (=8•7•6•5•4•3•2) способами.

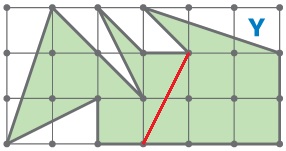
Задача 258. Это непростая задача. Прежде всего надо вычислить площадь данного многоугольника. В этом как раз и состоит наибольшая сложность. Площадь всех закрашенных частей равна 12 ед. кв. Значит, надо провести границу так, чтобы площадь каждой части была равна 6 ед. кв. Ниже приводим решение:

Задача 259. Необязательная.

Задача 260. Необязательная. Задача на повторение, предназначенная для сильных учащихся. Здесь ребенок должен сам догадаться, у кого из игроков есть выигрышная стратегия и как ее построить. Ключ к решению этой задачи – конфигурация поля для игры. Действительно, поле 7х7 – центрально-симметричная фигура. Поэтому для каждой его клетки найдется симметричная относительно центральной (по горизонтали и вертикали) клетки. Равновесная стратегия имеется у игрока, который первым сможет занять стратегически важную центральную клетку. Это, конечно, Первый игрок: он должен первым своим ходом раскрасить центральную клетку (4; 4). Дальше Первый будет «уравновешивать» ходы Второго, закрашивая клетку, центрально-симметричную относительно центра поля. Например, если Второй своим ходом закрасил клетку на две левее и на одну выше центральной, то Первый на следующем ходу раскрасит клетку на две правее и на одну ниже центральной. Таким образом, Первый всегда сможет сделать ход, если Второй его сделал. Рано или поздно Второй не сможет сделать следующий ход и проиграет.

Задача 261. Довольно простая задача, рассчитанная на средних и слабых учеников. Предлагать ее всем стоит только в том случае, если вы собираетесь подытожить ее соответствующими выводами, связанными с делимостью. Действительно, построим множество А = {2; 4; 6; 8; 10; 12; 14; 16; 18; 20; 22; 24; 26; 28} и В = {3; 6; 9; 12; 15; 18; 21; 24; 27}. Теперь построим пересечение этих множеств: {6; 12; 18; 24}. Что за числа оказались в этом множестве? Как видим, это все числа меньшие 30, которые делятся на 6. Учитывая то, что числа в пересечении должны делиться на 2 и на 3, можно виде гипотезы формулировать признак делимости на 6. В объединении множеств окажутся все числа, которые делятся хотя бы на одно из чисел – на 2 или 3: {2; 3; 4; 6; 8; 9; 10; 12; 14; 15; 16; 18; 20; 21; 22; 24; 26; 27; 28}.

Задача 262.

Задача 263.

Задача 264. Решений здесь, конечно, много. Приведем одно из них:

Задача 265.

Задача 266. Необязательная. Это довольно сложная задача, предназначенная для сильных учащихся. Основная ее сложность – догадаться, как здесь применить метод половинного деления. Для начала разделим все алмазы на две кучки по 34 штуки. Теперь будем брать из каждой кучки по одному алмазу и взвешивать алмазы попарно, получится 34 взвешивания. В каждой паре при этом обнаружится более легкий и более тяжелый алмаз. Будем откладывать все более легкие алмазы в левую кучку, а более тяжелые – в правую. В результате после 34 взвешиваний у нас получилось 2 кучки алмазов. Самый легкий алмаз совершенно точно находится в левой кучке, а самый тяжелый – точно находится в правой кучке. Заметим, что левая кучка совсем необязательно содержит только такие алмазы, каждый из которых легче всех алмазов из правой кучки. Но это и неважно, нам важно только то, что самый легкий алмаз находится в этой кучке, упорядочивать остальные алмазы по весу не входит в нашу задачу.

Возьмем левую кучку. В ней 34 алмаза, нужно найти самый легкий. За какое число взвешиваний это можно сделать? Разделим все алмазы снова на две кучки и сравним алмазы из кучек попарно, как мы делали в первый раз. В результате снова получим кучку более легких и кучку более тяжелых алмазов. Вторую кучку можно сразу отложить, она нам больше не понадобится (в ней нет ни самого легкого, ни самого тяжелого алмазов). Итак, мы истратили 17 взвешиваний и получили кучку из 17 алмазов, в которой снова надо найти самый легкий. Отложим один алмаз в сторону, а оставшиеся 16 снова разделим на две кучки и, потратив 8 взвешиваний, найдем кучку из 9 алмазов, среди которых есть самый легкий. Продолжаем процесс дальше – на следующем этапе мы потратим 4 взвешивания и получим кучку из 5 алмазов, среди которых есть самый легкий, и т. д. В результате мы находим в кучке из 34 алмазов самый легкий алмаз за 33 взвешивания.

Заметим, что тот же результат можно было получить без деления алмазов на кучки на втором этапе, а при помощи метода «всплывающего пузырька» (вспомните проект «Сортировки»!). Выложим 34 алмаза (кучка более легких) в последовательность и будем взвешивать соседние алмазы, начиная с конца и менять их местами, передвигая более легкий ближе к началу. В результате одного такого прохода самый легкий алмаз окажется первым в последовательности, и мы потратим 33 взвешивания. Аналогично (только начав взвешивания с начала последовательности), можно поработать с кучкой более тяжелых алмазов и найти в ней самый тяжелый алмаз за 33 взвешивания. Всего мы потратили 100 взвешиваний, как и требовалось в задаче.

Задача 267. Необязательная. Дети уже видели в нашем курсе много самых разных интересных случаев применения деревьев. Вот еще один такой пример. Здесь от ребят требуется описать с помощью дерева процесс приготовления торта, пользуясь рецептом, который мы приводим в задаче. Итак, элемент первого уровня – торт. Из каких полуфабрикатов он собирается на завершающей фазе приготовления? Из коржей, крема и глазури, значит, это элементы второго уровня (дети элемента «Торт»). Теперь опишем ветки, которые идут от элементов второго уровня. С приготовлением глазури все понятно: дети элемента «Глазурь» – это «Шоколадка» и «Молоко». С коржами не все так просто, потому что приготовление происходит в два этапа. Сначала яйца взбивают с песком, получается пена. Затем пену смешивают с маргарином и мукой. Значит, дети элемента «Коржи» – это «Пена», «Маргарин» и «Мука». В свою очередь, «Пена» – родитель элементов «Сахар» и «Яйца». Конечно, девочки, которые уже занимались приготовлением тортов, наверняка уточнят эту ветку, вставив еще один элемент – «Тесто». Действительно, из сахарно-яичной пены, муки и маргарина сначала получается тесто, а уж потом оно превращается в коржи. Это совершенно верно, но требовать такого «кулинарного» понимания проблемы от всех необязательно. Приготовление крема также идет в 2 этапа, поэтому соответствующая ветка будет иметь длину 3.

Задача 268.

Задача 269. Задача довольно простая, но тут требуется сообразительность. Своим первым ходом Первый должен сделать позицию симметричной. Как это сделать? Сколько камешков взять? Оказывается, надо взять одну (целую) кучу. Затем в точности повторять ходы Второго.