Компьютерное дополнение к курсу Информатика 6. 2024

Урок 31. «Автомат-сортировщик. Метод половинного деления»

В рамках этого проекта ребята знакомятся с методом половинного деления.

В данном проекте методическая и практическая цели практически совпадают: выйти на теоретический уровень обсуждения метода половинного деления, научить детей анализировать с помощью этого метода любые задачи на угадывание и решать такие задачи. Мы подходим к анализу игр на угадывание с точки зрения сортировки. По сути, так и происходит в играх на угадывание – после каждого нового вопроса буквы (или числа) сортируются на два множества (для ответа «Да» и для ответа «Нет»). Данный проект вообще интегрирует в себе почти все крупные блоки нашего курса: множества, последовательности, деревья, игры, сортировки.

Основные формы работы в этом проекте: индивидуальная, парная, фронтальная.

Работа проходит в три этапа.

 

1-ый этап. Знакомство с Половинным разделителем

В начале урока нужно предложить ребятам познакомиться с текстом «Автомат-сортировщик». В данном случае Автомат-сортировщик нужен нам больше для сюжета, он больше похож на сортировщика-человека, который работает в рамках определенных правил. По сути, можно было бы обойтись вообще без всяких исполнителей, просто договорившись, что в рамках этого проекта мы будем сортировать множества только так: всегда на два множества и всегда примерно пополам.

С деревом сортировки ребята уже знакомы из задач учебника, поэтому деревья, приведенные в учебнике на с. 133 и 134, будут ребятам понятны. После знакомства с текстом ребята переходят к решению задачи 209.

Задача 216. В русском языке 10 гласных букв. Из предшествующего текста ясно, что все деревья сортировки 10 букв Половинным разделителем имеют одинаковое число уровней. На первом уровне у него одно множество из 10 букв. На втором уровне – два множества, в каждом из которых по 5 букв. У каждого из этих множеств двое детей: в одном – 2 буквы, в другом – 3 буквы. Значит, на третьем уровне 4 множества: 2 – по две буквы и 2 – по три буквы. Каждое из них имеет двух детей (1 и 1 или 1 и 2). Значит, на четвертом уровне 8 множеств: 6 – по одной букве и 2 – по две буквы. Однобуквенные множества являются листьями. Двухбуквенные имеют по двое детей, которые являются листьями пятого уровня. Итак, деревья у ребят будут разными, но общий вид этих деревьев будет одинаковым – в дереве сортировки 5 уровней, значит, в сортировке было 4 этапа. К данной задаче мы не прилагаем никаких заготовок, поэтому ребята рисуют дерево и отвечают на вопросы в своих рабочих тетрадях.

 

2-ой этап. Знакомство с игрой «Угадай число»

На втором этапе урока ребята знакомятся с правилами новой игры. Мы надеемся, что правила игры Угадай число знакомы всем ребятам. Но если вы в этом не уверены, поясните правила, ответьте на вопросы детей. Возможно, вам покажется уместным провести несколько партий у доски с Водящим-учителем или Водящим-учеником, чтобы дети поняли, какие вопросы задавать можно, а какие – нет.

Ясно, что у Водящего во время игры не может быть никакой стратегии — ведь, выбрав число, он уже не может выбирать свои ответы, он должен всегда отвечать правдиво («Да» или «Нет»). Угадывающий же сам придумывает свои вопросы, от которых зависит, насколько быстро будет угадано число. Значит, цель анализа игры Угадай число — понять, какие вопросы должен задавать Угадывающий, чтобы отгадать число за заданное количество вопросов. При этом Угадывающий не должен рассчитывать на удачу, а должен задавать такие вопросы, чтобы они помогали угадывать быстро, какое бы число ни задумал Водящий.

Обсуждая возможные вопросы Угадывающего, сначала стоит выделить те из них, которые не приближают Угадывающего к победе, — лишние вопросы. Это могут быть вопросы, вообще не относящиеся к игре («Сколько будет пятью пять?»), или вопросы, ответы на которые заведомо ясны из предыдущих ответов Водящего. Например, понятно, что после утвердительного ответа на вопрос: «Это четное число?» вопрос: «Это число 5?» — лишний, и что стараясь угадать число за наименьшее количество вопросов, лишних вопросов задавать смысла нет. Также следует обсудить вопросы, которые помогут угадать число быстро при любом ходе игры, т.е. какое бы число ни загадал Водящий. Например, в случае утвердительного ответа Водящего на вопрос: «Это число 1?» можно угадать число за один вопрос, но в случае отрицательного ответа множество подходящих чисел может уменьшиться лишь на одно число, а значит, в этом случае мы не очень-то приблизимся к победе. Поэтому такой вопрос не может считаться удачным с точки зрения любой партии игры в Угадай число. Критерий удачного вопроса — разделение исходного множества в зависимости от ответа («Да» или «Нет») почти пополам — можно на этом этапе не формулировать явно, а упомянуть лишь вскользь, ведь на следующем этапе этот вопрос будет рассмотрен подробно.

Прежде чем перейти к решению задачи 210, все дети должны хорошо ориентироваться в правилах игры.

Задача 217. В данной задаче дети должны просто сыграть несколько партий в Угадай число. При этом Угадывающий и Водящий могут после двух первых партий поменяться местами. Вообще, применяя метод половинного деления, можно угадать любое число от 1 до 16 за 4 вопроса, но дети ведь будут играть пока как придется. Таблицы соревнований ребята составлять уже умеют. Озаглавить столбцы таблицы здесь лучше «Угадывающий» и «Водящий» и подсчитывать сумму побед Угадывающего и Водящего, вне зависимости от того кто кем был. Так вы сможете легко выявить пары, которые уже интуитивно (а может, и осознанно) используют метод половинного деления: если в какой-то из рабочих пар в четырех партиях выиграл Угадывающий, то это вряд ли произошло случайно. Таких

ребят стоит попросить поделиться своим опытом – это пригодится вам в дальнейшей работе.

Задача 218. Необязательная. Арифметическая задача на сообразительность. Общая сумма литров складывается из двух сумм – сумма литров во всех 10-литровых бидонах и сумма литров во всех 17-литровых бидонах. Сумма литров в 17-литровых бидонах в разряде единиц имеет 3 (поскольку сумма литров в 10-литровых бидонах кратна 10). Число бидонов по 17 литров можно найти, выяснив, произведение каких чисел на 17 оканчивается на 3. Это 9, 19, 29 и т.п. Поскольку 17 х 19 = 323 (т.е. больше общего числа литров молока), то нам подходит только число 9. Вычисляем 9 х 17 = 153. Вычитаем 223 – 153 = 70. Значит, бидонов по 10 л было 7.

Задача 219. Необязательная. Эту задачу проще решать достраиванием многоугольника Ш до прямоугольника. Заметим, что площадь одного из треугольников (нижнего), которым Ш будет достраиваться до прямоугольника, в свою очередь находится достраиванием (до прямоугольного треугольника), поскольку сам этот треугольник прямоугольным не является.

Ответ: площадь многоугольника Ш – 9 ½ ед. кв.

 

3-ий этап. Знакомство с методом половинного деления

Как видите, на первом этапе проекта мы занимались сортировкой, на втором этапе – игровой стороной дела. Теперь пришло время соединить все это воедино и сделать выводы. Предложите ребятам познакомиться с текстом «Метод половинного деления» на с. 132–133. Оказывается, чтобы спланировать заранее игру для любого числа, нужно построить дерево вопросов. Каждому такому дереву вопросов соответствует дерево сортировки Простым автоматом. При этом минимальное число вопросов получится в том случае, если дерево сортировки будет минимальной высоты. Значит, это дерево сортировки Половинным разделителем! Отсюда получается очень простой вывод – при игре на угадывание нам нужно вести себя как Половинный разделитель: задавать такие вопросы, чтобы множество на

каждом этапе в зависимости от ответа («Да» или «Нет») делилось примерно пополам. Оказывается, таким методом можно не только анализировать игры на угадывание, но и решать задачи. Мы будем называть такой способ методом половинного деления. После знакомства с теорией ребята переходят к решению задач.

Задача 220. В процессе решения этой задачи ребята на практике устанавливают связи между деревом сортировки Половинным разделителем, деревом вопросов и игровым процессом. Для решения этой задачи ребята используют заготовки деревьев. Лучше вложить (вклеить) их в тетрадь. В дерево дети вписывают вопросы. Вопросы должны быть составлены с помощью метода половинного деления, т. е. должны делить каждое множество чисел пополам. Конечно, дерево вопросов (и соответствующее дерево сортировки) могут быть разными.

В другое дерево ребята записывают множества чисел, на которые делятся множества на каждом этапе в зависимости от ответа на вопросы из дерева. Таким образом, дерево вопросов и дерево сортировки должны полностью соответствовать друг другу. Построенные деревья позволяют сделать вывод, что число от 1 до 16 в любой партии можно угадать за 4 вопроса.

После того как деревья будут построены, ребята снова разбиваются на пары и играют в Угадай число от 1 до 16. Теперь уже всегда должен выигрывать только Угадывающий (можно снова заполнить таблицу соревнования).

Задача 221. Эта задача по объему несколько меньше, чем предыдущая. Здесь мы не предлагаем строить дерево вопросов, а лишь предлагаем построить дерево сортировки Половинным разделителем. Однако для игрового процесса все равно понадобятся вопросы, поэтому придумывать их все равно придется, но можно не записывать. В отличие от предыдущей задачи здесь множества не всегда будут делиться поровну. Поэтому не все листья будут расположены на последнем уровне. Поскольку в данном дереве 6 уровней, то этапов сортировки – 5. Число от 1 до 25 можно наверняка угадать за 5 вопросов.

После построения дерева обязательно надо поиграть в парах. Если кто-то из ребят правильно построил дерево, но не может угадать число за 5 вопросов, значит, он пока не может сопоставить дерево сортировки с реальным игровым процессом. В таких случаях нужно убедиться, что ребенок может для каждого этапа сортировки придумать соответствующий игровой вопрос, или придумать вопросы вместе с ним.

Задача 222. Необязательная. Здесь ребятам предстоит анализировать новую (но очень похожую) игру. Решается эта задача аналогично предыдущей – сначала строится дерево сортировки Половинным разделителем, а затем проводится несколько партий с использованием метода половинного деления.

Если вы чувствуете, что ваши ребята уже вполне освоились с методом половинного деления, можно не строить дерево, а сразу начать с игры в Угадай букву. Если кто-то из детей при этом не угадывает букву за 6 вопросов, ему необходимо вернуться к построению дерева и явному формулированию соответствующих вопросов.

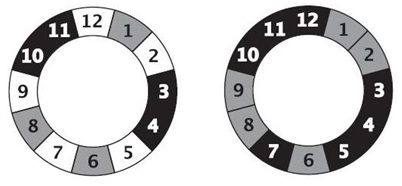
Задача 223. Необязательная. Понять закономерности этой игры, как всегда, проще, если сыграть парами несколько партий. Позиций в этой игре всего 12, поскольку в игре никак не учитывается то, сколько кругов обошла стрелка, прежде чем оказалась на данной цифре. Раскрашивать позиции, как всегда, надо начинать с заключительной позиции – 6 (она проигрышная). Далее мы находим все позиции, из которых можно попасть в 6 за один ход (4 и 3) и раскрашиваем их как выигрышные. Теперь следует найти позицию, в результате любых ходов из которой получаются только уже раскрашенные позиции. Это позиция 1, она будет проигрышной. Снова ищем позиции, из которой можно попасть только в уже раскрашенные – раскрашиваем позиции 10 и 11 как выигрышные, затем позицию 8 как проигрышную (см. рис. справа). Итак, мы «обошли» один круг, но не все позиции оказались раскрашенными. Придется сделать еще один круг. В проигрышную позицию 8 можно попасть из позиции 5, значит, 5 – выигрышная позиция (позиция 6 уже раскрашена, ее не рассматриваем). Так двигаемся дальше, пока вся числовая линейка не будет раскрашена. Начальная позиция 12 – выигрышная, значит, выигрышная стратегия есть у Первого.