Компьютерное дополнение к курсу Информатика 6. 2024

Уроки 22–23. «Цикл «пока». Свойства цикла «пока». Составление алгоритма с циклом «пока»

На этом листе определений мы продолжаем знакомство с учебным алгоритмическим языком.  Учащиеся уже знают, как выполнить команду или последовательность команд несколько раз: для этого используется команда цикл n раз. Бывают, однако, ситуации, когда нам требуется многократное выполнение тела цикла, но мы не знаем точно, сколько именно раз. Такое случается и в жизни: объясняя кому-то дорогу, мы говорим: «Иди прямо, пока не упрешься в бетонный забор». При этом мы не знаем и не уточняем, какое именно расстояние надо пройти по прямой. То же самое (и очень часто) случается и в программировании:  мы хотим, чтобы исполнитель выполнял какие-то действия, но только до того момента, пока для этого имеются подходящие условия. В случае с Роботом на листе определений описана типичная ситуация – стена, которая находится на неопределенном расстоянии. Если мы знаем это расстояние, мы используем команду цикл n раз, а вот для случаев, когда расстояние не известно, и используется новая команда – цикл пока. Смысл этой команды совершенно прозрачен: пока выполняется некоторое условие, делай то-то и то-то. Формально это записывается так:

Команда цикл пока гораздо сложнее для понимания, чем команда цикл n раз. Поэтому советуем вам очень внимательно отнестись к тем детям, которые что-то не поняли или не так поняли. Что здесь важно понимать? Тело цикла выполняется, только если выполнено условие. Как только условие перестает выполняться, Робот сразу же переходит к строчке кц и затем – к следующей команде. А если условие с самого начала не выполняется? В этом случае тело цикла не будет выполнено ни разу. А если условие будет выполняться всегда? Тогда и тело цикла будет выполняться бесконечно. Такие ситуации нередки, даже слово специальное придумали – зацикливание. Конечно, зацикливание – ситуация нежелательная, поэтому при составлении команды цикл пока надо четко понимать, какую задачу мы хотим решить, при каких условиях тело цикла следует выполнять и при каких – закончить. Хорошо бы команду протестировать, выполнив несколько раз тело цикла и посмотрев на результат. Еще очень важно понимать, что условие проверяется каждый раз перед выполнением тела цикла, но не проверяется в процессе его выполнения. То есть если в теле цикла содержится много команд, то ученик сам должен просчитывать, не приведут ли некоторые из них к отказу в случае изменения каких-то условий.  И еще пара замечаний. Из логики самой команды цикл пока следуют две важные вещи. Если исполнитель приступил к выполнению тела цикла, это означает, что условие выполнено. Если выполнение команды цикл пока завершилось, значит,  условие не было выполнено. Вот это ребята должны понимать. Со слабыми детьми можно устроить небольшую импровизацию: пусть поработают исполнителем и выполнят несколько команд цикл пока при различных условиях. На практике дети скорее прочувствуют физический смысл команды и поймут, как она работает.

Задача 141. Несложная задача, помогающая усвоить новый материал.

Рассмотрим сначала ситуацию, когда Робот стоит в незакрашенной клетке.

Цикл 1

Компьютер: клетка чистая?

Робот: да

Компьютер: закрасить

Компьютер: клетка чистая?

Робот: нет

 

Цикл 2

Компьютер: клетка закрашена?

Робот: нет

 

Теперь рассмотрим ситуацию, когда Робот стоит в закрашенной клетке.

Цикл 1

Компьютер: клетка чистая?

Робот: нет

 

Цикл 2

Компьютер: клетка закрашена?

Робот: да

Компьютер: закрасить

Компьютер: клетка закрашена?

Робот: да

Компьютер: закрасить

            Зацикливание

 

Задача 142. Простая задача на закрепление материала листа определений. На стр. 88 приведен алгоритм вниз до стены, использующий команду цикл пока:

Это, так сказать, канонический алгоритм и по его подобию можно написать алгоритмы вправо до стены, вверх до стены и влево до стены, только вместо команд внизу свободно и вниз следует ставить команды, соответствующие алгоритму: например, в алгоритме вправо до стены это должны быть команды справа свободно и вправо. Впрочем, учащиеся могут написать и другие алгоритмы – это их право, главное – чтобы были выполнены все условия задачи, а именно – чтобы не было отказа и чтобы цикл не выполнялся вечно.

Задача 143. Несложная задача в продолжение знакомства с командой цикл пока. Здесь от ребенка требуется написать только один вспомогательный алгоритм – вправо до стены с закрашиванием. Ребята, скорее всего, догадаются использовать уже написанный в предыдущей задаче алгоритм вправо до стены, добавив в него команду закрась. Только пусть обязательно проверят, как он работает: чтобы делал то, что нужно, не зацикливался и не вызывал отказа.

Задача 144. Довольно трудная задача, продолжающая серию задач на команду цикл пока.  Здесь, прежде всего, надо хорошенько подумать, как использовать цикл оптимальным образом. Итак, Робот стоит в левом нижнем углу, и у нас есть вспомогательный алгоритм закрасить ряд вправо и вернуться. Для удобства самый нижний ряд мы оставим на потом, а пока займемся закрашиванием вышележащих рядов:

Далее следует вернуть Робота в исходную позицию, для этого используем алгоритм вниз до стены со стр. 88. И, конечно, надо не забыть закрасить самый нижний ряд клеток:

закрасить ряд вправо и вернуться

Задача 145. Это сложная задача, являющаяся продолжением предыдущей. Решать ее можно, конечно, по-разному. Но наиболее эффективным будет такое решение. Сначала вернем Робота в левый нижний угол, а затем выполним алгоритм закрасить прямоугольник из предыдущей задачи. А поставить Робота в левый нижний угол совсем просто:

влево до стены

вниз до стены

Задача 146. Простая задача на разрезание многоугольников.

Ответ:

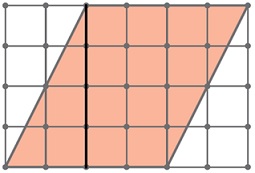
Задача 147. Продолжаем составлять алгоритмы для Робота с командой цикл пока. Здесь точные размеры стены нам неизвестны. Будем исходить из того, что ее длина равна, по крайней мере, 1 клетке.

а) Обойдем стену справа:

Выполнив эту команду, Робот окажется на 1 клетку правее конца стены. Теперь шагаем вниз и 1 раз влево (т.к. длина стены может равняться 1, дальше налево идти не имеет смысла – можно оказаться за ее пределами):

Итак, вот искомый алгоритм:

б) Используем алгоритм обход стены справа из п. а). Далее Робот раскрашивает клетку и делает шаг влево – пока выполняется условие сверху стена:

в) Используем алгоритм раскрасить под стеной из п. б).  После его выполнения у нас раскрашены все клетки под стеной, а Робот находится на первой чистой клетке после этого закрашенного ряда.  Ему остается шагнуть вверх и вправо, после чего выполнять пару команд (закрась, вправо), пока под ним остается стена:

Задача 148. Трудная задача, в которой можно использовать команду цикл пока. С одной стороны, нам надо отслеживать стенку сверху, чтобы обнаруживать выходы и закрашивать их. С другой – этот процесс не должен продолжаться бесконечно: чтобы вовремя его остановить, мы должны отслеживать стенку снизу. Очевидно, нам придется использовать вложенный цикл пока. Вот искомый алгоритм:

Можно использовать и другой алгоритм,  с применением условной команды если …то …иначе:  

Задача 149. Трудная задача на сообразительность. Если учащийся затрудняется с решением с помощью предлагаемой в условии схемы, то можно натолкнуть его на такие рассуждения. Какие у нас вообще возможны группы учащихся по составу отметок? Можно найти их, построив дерево перебора всех вариантов:

«5»; «4»; «3»

«5;4»; «5;3»; «4;3»

«5;4;3»

Известно, что пятерки имеют 18 человек:

«5» + «5;3» + «5;4» + «5;3;4» = 18

Известно, что четверки имеют 24 человека:

«4» + «5;4» + «3;4» + «5;3;4» = 24

Учитывая, что «3» = «5» = 3, а также «5+4» = 5, перепишем вышеприведенные равенства:

3 + «5;3» + 5 + «5;3;4» = 18 или «5;3» + «5;3;4» = 10

«4» + 5 + «3;4» + «5;3;4» = 24 или «4» + «3;4» + «5;3;4» = 19

Теперь соединим всю известную нам информацию:

«5;4» = 5

«5» = 3

«5;3» + «5;3;4» = 10

«4» + «3;4» + «5;3;4» = 19

«3» = 3

Складываем все указанные числа: 5+3+10+19+3= 40. Заметим, что здесь выписаны все возможные группы учащихся по составу отметок, при этом группа «5;3;4» выписана 2 раза. Но всего в классе 31 человек, значит,  «5;3;4» = 9. Тем самым мы нашли ответ на первый вопрос. На второй вопрос задачи мы могли бы ответить с самого начала. Если четверки имеют 24  человека, то не имеют четверок 31 – 24 = 7 человек.

Задача 150. Построение геометрических фигур заданной площади.

Задача 151. Необязательная. Довольно сложная задача, предназначенная для самых сильных учеников. Лучше всего вначале поиграть парами в эти новые «Крестики-нолики», чтобы понять специфику данной игры и отличие ее от обычных Крестиков-ноликов. В процессе такой игры ребята поймут, что самой выгодной (стратегической) позицией является вторая слева клетка в нижнем ряду. Действительно, пусть Первый поставит туда свой первый крестик. Что будет происходить дальше? Если Второй поставит свой нолик не в нижнем ряду, то на следующем ходу Первый создаст в нижнем ряду как называемую «вилку», поставив крестик в третью клетку слева в нижнем ряду. Теперь, куда бы ни сделал ход Второй, на своем третьем ходу Первый выигрывает, поставив еще один крестик в нижний ряд. Допустим, Второй на своем первом ходу уже занял нужную Первому клетку нижнего ряда (третью слева). Тогда Первый на своем втором ходу ставит крестик в центр поля – вторую клетку слева в среднем ряду. Дальше Второй вынужден поставить нолик в угол (чтобы Первый не построил диагональный ряд крестиков). Тогда на своем третьем ходу Первый снова создает «вилку», поставив крестик в первую клетку среднего ряда и в любом случае выигрывает на четвертом ходу.

Задача 152. Необязательная. Трудная задача на логику и сообразительность. Поскольку дерево игры здесь будет довольно громоздким, можно дать детям возможность сыграть несколько партий в 7 камней. Пусть на опыте убедятся, что каков бы ни был процесс игры – результат всегда будет один и тот же – 7 кучек по 1 камню. Поэтому в каком порядке мы будем разбивать эти  7 на кучки по 1 камню, совершенно не важно, ибо число ходов всегда будет равняться 6. То есть последним всегда будет ходить Второй, а значит, и выигрывать всегда будет Второй.

Задача 153. Необязательная. Сложная задача, предназначенная для самых сильных учащихся. На первый взгляд, задача очень напоминает задачу на перебор всех путей, однако выстроить решение с помощью формального построения дерева перебора оказывается слишком сложно. Как видите, маршрут у Печкина довольно затейливый и перебор будет крайне большим. Поэтому здесь необходимо провести некоторые геометрические рассуждения. Например, выяснить, в каком доме живет сам Печкин. Он живет в доме, в который ведут 3 тропинки, – ведь по одной тропинке Печкин принес почту, по другой потом ушел, по третьей вернулся обратно. Итак, Печкин живет в доме 4. В каком доме может жить дядя Федор? В доме, к которому ведут 4 тропинки, ведь в этот дом Печкин заходил дважды и каждый раз шел разными тропинками. Значит, дядя Федор может жить в доме 2, 6 или 7. С почты Печкин может попасть в те же самые дома. Переберем эти три варианта. Пусть Печкин с почты пошел в дом 2, затем в 3, 4, 5, 6, 7, 1. Затем Печкин вернулся снова к дому 2. Чтобы попасть на почту, Печкину теперь придется идти сначала к дому 7 (чтобы не проходить дважды по одной тропинке). Затем Печкин берет посылку и идет в дом 6 к дяде Федору, а затем отправляется домой. Таким может быть маршрут Печкина. Аналогично можно построить решение, если Печкин сначала пойдет в дом 7. А вот если мы предположим, что Печкин сначала идет в дом 6, то маршрут не выстраивается. Видим, что в обоих случаях дядя Федор живет в доме 6.