Компьютерное дополнение к курсу Информатика 6. 2024

Урок 20. «Выигрышная стратегия. Выигрышные и проигрышные позиции»

Выигрышная стратегия

Постепенно мы переходим от формальной работы с цепочками партий к их содержательному анализу. Действительно, до этого момента учащиеся составляли цепочки партий, соблюдая правила игры и, возможно, некоторые условия (выигрыш определенного игрока, определенную длину цепочки партии игры, данную заключительную позицию и пр.). При этом ребята совершенно не должны были задаваться вопросами, насколько вероятна такая партия в жизни, насколько умело и старательно играют Первый и Второй и стремятся ли они выиграть. Чтобы соблюсти условия задачи, при построении цепочки партии ребята могли и «подыгрывать» определенному игроку, заставляя противника играть неразумно, поддаваться. Все это мы уже отмечали раньше, равно как и то, что некоторые ребята все же будут стараться построить цепочку «честной» («разумной») партии, считая ситуацию формального построения цепочки партии неестественной. Заметим, что рисуя дерево, мы также не сопоставляем его с процессом реальной игры, а лишь отражаем на дереве все возможные партии, как «разумные», так и «неразумные». 

Теперь пришло время выделить из множества всех возможных партий разумные партии, т. е. такие, в которых каждый игрок стремится к победе и не поддается противнику (при этом, конечно, играет честно, соблюдает правила игры). Это значит, что если игрок может с помощью некоторого хода (или серии ходов) выиграть, то он в разумной партии сделает именно этот ход (или серию ходов).

Само наличие, а тем более построение выигрышной стратегии для одного из игроков – действительно сложный для понимания материал. Для того чтобы это понять, детям понадобится время, поэтому мы подходим к этому последовательно, небольшими шагами.

 

Выигрышные и проигрышные позиции

Для начала мы изучаем самую простую игру - Камешки. В этой игре возможных позиций немного и они легко упорядочиваются – это отрезок числовой прямой от нуля до некоторого оговоренного числа (начальной позиции игры). Полное дерево игры Камешки тоже относительно небольшое – его можно уместить на одной странице (конечно, только для игр с небольшими начальными позициями).

Начнем с самого простого – изучения отдельных позиций: какие из них являются выигрышными, а какие – проигрышными. На самом деле мы изучаем не собственно позицию, а всю игру из этой начальной позиции. Но пока позиции до того небольшие, что говорить об игре сложно: она тривиальна и заканчивается, практически не успев начаться.

Что же означает «изучить позицию»? Для каждой отдельно взятой позиции мы выясняем, сможет ли выиграть из этой позиции игрок, чья очередь ходить. При этом мы должны рассмотреть все возможные варианты ответных ходов противника. Обратите внимание, что мы теперь не говорим о Первом и Втором игроках. В наших рассуждениях пока неважно, игроку с каким именно номером досталась рассматриваемая позиция – Первому или Второму. Важно только то, что мы исследуем выигрышность позиции с точки зрения игрока, чей черед делать ход.

Для рассмотрения на листе определений мы выбрали игру Камешки, в которой разрешено брать 1, 3 или 4 камешка на каждом ходу. Такой набор разрешенных ходов не случаен: при более простых разрешенных ходах раскраска числовой линейки получается периодической, и это может привести детей к нежелательным обобщениям.

Перейдем теперь к позициям с бо́льшим числом камешков. Здесь нам понадобится провести некоторые рассуждения. Представим себе, что мы играем в Камешки и хотим выиграть. Чтобы выиграть (независимо от того, какие ходы будет выбирать противник), нам надо постараться поставить нашего противника в невыгодное положение. В идеале хорошо было бы играть так, чтобы противнику просто некуда было деться: какой ход он ни сделает, все равно останется в проигрыше. Что это значит в нашем случае? Это значит, что надо оставить противнику такую позицию, из которой при любом его ходе нам достанется выигрышная  позиция.

Как видите, чтобы полностью разобраться в ситуации, нам пришлось проделать много достаточно сложных рассуждений. Главное, что должны понять дети после изучения листа определений: чем выигрышная позиция отличается от проигрышной. Также они должны уметь раскрашивать позиции на числовой линейке.

Итак, если начальная позиция выигрышная, то выигрышную стратегию имеет Первый, если проигрышная – Второй. Изложенное общее правило выигрыша – стараться оставлять противнику проигрышную позицию (оно верно для любой игры, где позиции можно разделить на выигрышные и проигрышные) – в каждой игре Камешки реализуется по-разному. Раскраска клеток числовой линейки определяет как игрока, обладающего выигрышной стратегией, так и его ходы (правило следования выигрышной стратегии).  Правило выигрыша может быть сформулировано либо в виде последовательности ходов, которые должен делать игрок, либо в виде правила о том, какие позиции должен оставлять противнику данный игрок (если проигрышные позиции подчиняются какой-то общей закономерности).

Выигрышные и проигрышные позиции существуют и в других играх, кроме Камешков. Но изучение других игр связано с дополнительными трудностями. Так, в отличие от игры Камешки, в играх Ползунок, Сим, Крестики-нолики все возможные позиции придется размещать на дереве игры, которое чаще всего будет очень большим, поэтому возникают чисто технические трудности. В игре Камешки позиции Первого и Второго ничем не различаются, поэтому можно говорить, что некоторая позиция является выигрышной или проигрышной для игрока, который должен делать из нее  ход, и анализировать игру Камешки одновременно как для Первого, так и для Второго. В игре же Крестики-нолики ситуация иная: в этой игре каждый игрок изменяет позицию по-своему, ставит свой знак, и поэтому каждую позицию нужно анализировать для каждого игрока в отдельности. Также следует заметить, что далеко не в любой игре все позиции можно разделить на выигрышные и проигрышные для игрока, который должен делать ход.

 

Задача 116. Первое задание данной задачи – продолжение работы, начатой на листе определений.

Начинаем со следующей (по сравнению с листом определений) нераскрашенной позиции – 9. Возможные ходы игры – 1, 3 и 4, значит, из позиции 9 могут получиться позиции 8, 6 и 5. Все эти три позиции выигрышные, значит, позиция 9 – проигрышная.  Если кто-то из ребят затрудняется, поработайте вместе над позицией 9, используя наводящие вопросы: «Какие ходы может сделать игрок?», «Какие позиции могут получиться из позиции 9 в результате одного хода?», «Есть ли среди них проигрышные?», «Выигрышной или проигрышной является позиция 9?».

Из позиции 10 в результате хода могут получиться проигрышные позиции 9, 7 и  выигрышная 6. Есть проигрышные позиции, значит, позиция 10 – выигрышная.

Рассуждая и дальше таким же образом, получаем следующую раскрашенную числовую линейку до позиции 15:

Теперь, пользуясь раскрашенной числовой линейкой, учащиеся могут выполнить оставшиеся части задания. Позиция 15 – выигрышная, значит, в рассматриваемой игре Первый игрок имеет выигрышную стратегию: он должен выбирать каждый раз такой ход, чтобы он приводил к проигрышным позициям: 14, 9, 7, 2 (и 0). Требуемая последовательность позиций выглядит так:

15–14–13–9–8–7–6–2–1–0

 

Задача 117. Как видно из числовой линейки, раскрашенной при решении предыдущей задачи, позиция 14 – проигрышная. Это означает, что Первый выигрышной стратегии не имеет, а значит, выигрышной стратегией обладает Второй. Выигрышная стратегия, как всегда, состоит в том, чтобы оставлять противнику только проигрышные позиции: 9, 7, 2 и 0. Вот два примера партий, в которых Второй следует выигрышной стратегии:

 

14–11–9–8–7–3–2–1–0

14–13–9–5–2–1–0

 

Как именно учащийся сформулирует выигрышную стратегию – не очень важно. Главное, чтобы им была выражена правильная мысль о том, что Второй должен каждый раз брать столько камешков, чтобы оставлять Первому проигрышную позицию. Еще одна важная мысль, которая должна быть озвучена в описании выигрышной стратегии, – то, что она не зависит от игры противника, предусматривает ответ на все возможные ходы Первого. Вот пример описания выигрышной стратегии Второго:

1. После первого хода Первого в куче останется 13, 11 или 10 камешков. Второй должен взять, соответственно, 4, 4 или 1 камешек – тогда в куче останется 7 или 9 камешков.

2. Если в куче осталось 9 камешков, то после следующего хода Первого может остаться 8, 6 или 5 камешков. Тогда Второй должен взять, соответственно, 1, 4 или 3 камешка – в куче останется 7 или 2 камешка.

3. Если в куче осталось 7 камешков, то после следующего хода Первого может остаться 6, 4 или 3 камешка. Тогда Второй должен взять, соответственно, 4, 4 или 1 камешек – в куче останется либо 2 камешка, либо игра окончится выигрышем Второго (0 камешков).

4. Если в куче осталось 2 камешка, то Первый может забрать только 1 камешек. На следующем  ходу Второй забирает последний оставшийся камешек и выигрывает.

Задача 118. Задача, наверное, была бы слишком сложной, если бы к ней не прилагалось столь подробное указание. Если ребенок будет точно следовать этому указанию, то единственной сложностью для него в этой задаче будет найти и сформулировать закономерность раскраски числовой линейки, а затем на основе этого сформулировать выигрышную стратегию. Причем формулировать выигрышную стратегию уже нужно будет не пошагово, описывая каждый ход игры, а в виде общего правила, которое бы определяло, позиции какого вида должен оставлять противнику игрок, обладающий выигрышной стратегией.

Ответ:

Проигрышными являются все позиции, количество камешков в которых кратно трем. Число 214 не кратно трем, поэтому позиция 214 является выигрышной. Поэтому в игре с начальной позицией 214 выигрышную стратегию имеет Первый. Он должен на каждом своем ходу брать столько камешков, чтобы число камешков, оставшихся в куче после его хода, было кратно трем.

Задача 119. Задача средней сложности о составлении алгоритма для Робота с условными конструкциями.

Решение осложняется тем, что мы не знаем расположения коридора, в котором находится Робот. Коридор может идти в направлении снизу вверх или слева направо. Если коридор горизонтальный, Робот может идти как направо, так и налево. Если же коридор вертикальный, то Робот может идти либо вверх, либо вниз. Будем выводить Робота вверх и влево. От места, где находится Робот, до выхода в любую сторону – не больше 15 шагов. Идея решения такова. С помощью условной конструкции ищем проход:

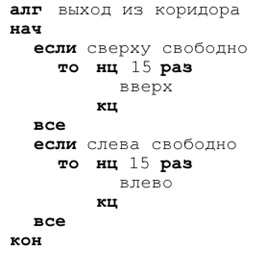
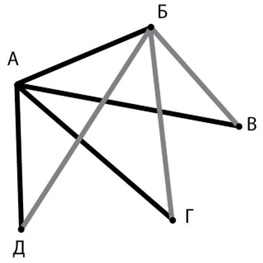
Задача 120. Необязательная. Проще всего решить эту задачу, нарисовав схему (граф).  Дадим пятерым друзьям имена: А, Б, В, Г и Д. А должен пожать руку каждому из остальных четверых друзей (4 черные линии на графе справа). Б тоже должен пожать руку четверым, но рукопожатие с А на нашей схеме уже есть. Проводим из точки Б еще 3 отрезка (серые линии на нашей схеме). Продолжая соединять точки на графе, получаем всего 10 отрезков – это число и будет ответом задачи.

Задача 121. Знакомство с правилами новой игры (новой для всех, ведь, скорее всего, дети в такую игру не играли) – очень полезное занятие. Освоиться с новой игрой, конечно, лучше всего, просто начав в нее играть. Именно в процессе игры правила станут понятными до конца и тогда можно будет приступить к построению выигрышной стратегии для этой игры (задача 122). Как проводить турнир и заполнять таблицу, дети уже должны знать – см. задачу 94.

Задача 122. Здесь ребята впервые сталкиваются с тем, что раскрашивать выигрышные и проигрышные позиции и строить выигрышные стратегии можно не только для игры Камешки. В данной игре начальная позиция – число 0, а заключительная – число 100, поэтому начинать раскрашивать линейку нужно с заключительной позиции 100 и раскрашивать позиции по убыванию до тех пор, пока не выяснится общая закономерность чередования проигрышных и выигрышных позиций в данной игре. Подробное указание к задаче позволяет сделать ее доступной для всех, даже для слабых учащихся.

Итак, 100 – проигрышная позиция для игрока, чья очередь делать ход (на предыдущем ходу противник назвал число 100 и уже выиграл). Позиция 99 – выигрышная, так как из нее за один ход можно получить проигрышную позицию 100, для этого нужно прибавить 1. Аналогично, выигрышными являются позиции 98–91. Теперь рассмотрим позицию 90. В результате любого хода из позиции 90 получается выигрышная позиция (91, 92, …, 99), значит, позиция 90 – проигрышная. Так ребята движутся по числовой линейке, пока им не становится ясно, что проигрышные позиции – все числа, кратные 10, а все остальные – выигрышные. Таким образом, позиция 10 – проигрышная, позиции 9, 8, 7, …, 1 – выигрышные, а ноль – проигрышная. Значит, выигрышная стратегия есть у Второго. Она заключается в том, чтобы на каждом своем ходу прибавлять такое число, чтобы в результате получалось  число, кратное 10.

Задача 123. Повторение темы «Когда утверждения не имеют смысла». Первое утверждение не имеет смысла, если седьмой бусины в последовательности нет (ясно, что несколько седьмых бусин в одной последовательности не бывает). Это означает, что длина последовательности Г должна быть меньше семи. Так как в условии указано, что ее длина должна быть не меньше пяти, значит, в последовательности Г 5 или 6 членов.

Второе утверждение не имеет смысла, если последняя бусина последовательности – круглая. Возможно, кто-то из детей решит, что если в последовательности вообще не будет круглых бусин, то второе утверждение будет бессмысленным. Однако это не так. Оказывается, для такой последовательности второе утверждение истинно! Это слишком трудный для понимания факт, поэтому мы его с детьми не обсуждали. Поэтому стоит просто указать на это ребенку и попросить придумать другой случай бессмысленности.

Аналогично, третье утверждение не будет иметь смысла только для такой последовательности, в которой первая бусина – квадратная.

Задача 124. Решая задачи 112 и 113, дети познакомились с правилами игры Ползунок и нарисовали пару последовательностей позиций для этой игры.

В этой задаче мы начинаем готовить ребят к проекту «Стратегия победы». Для успешной работы с проектом необходимо уметь строить дерево игры и уметь это дерево анализировать. Отметим, что обычно при анализе дерева мы рассматриваем каждую отдельную позицию с точки зрения одного игрока – того, который должен делать ход (ведь именно он решает, как ему лучше пойти, чтобы выиграть).  Просматривая дерево, мы пытаемся ответить на вопросы: «Какой ход игрока наверняка приведет его к победе, т. е. при любых дальнейших ходах противника?», «Какой ход наверняка приведет к проигрышу, а какой может дать и тот и другой исход?»

Так и в жизни: нашим детям необходимо, с одной стороны, представлять все возможные выходы из данной ситуации, а с другой – оценивать вероятность выигрыша в каждой из них для себя и окружающих. Только в этом случае  можно успешно обходить все рифы и мели. Например, ученик, обдумывая, когда выйти из дома, должен хорошо представлять себе: если он придет в школу за 15 минут до начала занятий, то наверняка не опоздает и его день начнется нормально;  если влетит через 15 минут после звонка, то наверняка его день начнется с замечания в дневнике; если же войдет в школу со звонком, то возможно и то и другое, в зависимости от ситуации (скорости бега до кабинета, возможной встречи с директором, настроения учителя и т. п.).

В данной задаче часть дерева игры Ползунок уже построена. Нужно проанализировать ее и ответить на вопросы задания. Чтобы выяснить, какой игрок должен ходить в позиции А, нужно просто сосчитать количество единичных отрезков в ломаной позиции А: их 13, нечетное число, значит, очередь делать ход Второму.

Исследовать позиции, как и раньше, надо, начиная с заключительных позиций.  В дереве L 6 листьев, все позиции в листьях заключительные, обводим их имена (Л, Е, М, З, И, Н) синим. Каждая позиция, предыдущая перед заключительной, является выигрышной – обводим эти позиции (Д, Б, Ж, В, К) красным. Остались необведенными только позиции Г и А. Из позиции Г возможен только один ход, приводящий к выигрышной позиции, значит, позиция Г – проигрышная. Из позиции А есть ход, приводящий к проигрышной позиции, значит, позиция А – выигрышная. Таким образом, выигрышную стратегию Второго из позиции А можно записать в виде последовательности позиций так: А–Г–К–Н. Конечно, обычно стратегия не описывается при помощи только одной   последовательности позиций, но в данном конкретном случае именно так и получилось – каждый раз у Первого есть только один возможный ход.

Задача 125. Необязательная. На первый взгляд, это очередная задача на исследование игры – нужно раскрасить шахматную доску, и станет ясно, кто из игроков имеет выигрышную стратегию при игре из каждой начальной позиции. На самом деле ситуация здесь, с одной стороны, более сложная, а с другой – более простая, тривиальная, как говорят математики.

Давайте сначала пойдем по обычному пути – исследуем позиции, раскрасим шахматную доску (см. рис. на стр. 78). Видим, что проигрышных позиций на доске столько же, сколько выигрышных. Чтобы разобраться, почему в этой игре выигрышная стратегия не нужна, нужно попытаться в эту игру сыграть или построить несколько последовательностей позиций:

 

d3–d2–c2–(4; 2)–b2–b1–a1

e3–d3–c3–b3–a3–a2–a1

 

Построив несколько партий из различных начальных позиций, ребенок поймет, что, действительно, игра предопределена начальной позицией – ведь у игроков практически нет выбора, какой ход делать – длина любой партии из заданной начальной позиции будет всегда одной и той же, а значит, и исход этой партии будет всегда одним и тем же: если партия начинается с любой закрашенной клетки шахматной доски, то выигрывает Первый, если с незакрашенной – выигрывает Второй.

Таким образом, игра Пешка – вырожденная, правила этой игры настолько сковывают действия игроков, что исход игры предопределен изначально. Сделать такой вывод, обобщить, объяснить себе и учителю, почему так происходит, – дело не такое простое для шестиклассника. Поэтому эта задача помечена как необязательная.

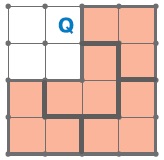
Задача 126. Необязательная. Повторение темы «Многоугольники на сетке». Прежде чем пытаться вычленять многоугольники, надо подсчитать общую площадь данного многоугольника и поделить ее на 4. Получаем, что площадь каждого из четырех искомых многоугольников равна 3 ед.кв. Могут ли эти 3 квадрата быть вытянуты в линию? Беглый анализ фигуры Q показывает, что ответ отрицательный. Значит, 3 квадрата образуют угол. Вот решение задачи:

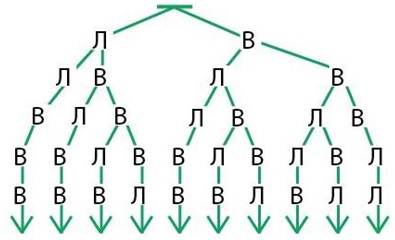
Задача 127. Необязательная. Для решения задачи нужно построить дерево перебора, например такое, как на рис. справа. После того как дерево будет простроено, станет видно, что для пешки всего существует 10 разных путей. При построении этого дерева в качестве обозначения ходов пешки мы использовали просто буквы: Л – для «влево» и В – для «вверх». Именно так можно предложить сделать ребенку, который застопорился на этапе выбора   обозначений.  Хотя, конечно, именно такой выбор не обязателен: можно использовать и стрелки, и просто отрезки (вертикальный и горизонтальный) или какие-то совсем отвлеченные значки, если ребенок сможет объяснить (и записать!), как и что он обозначил.