Компьютерное дополнение к курсу Информатика 6. 2024

Уроки 11–13. «Алгоритмы: цикл «N раз»

Мы продолжаем знакомить детей с учебным алгоритмическим языком. На данном уроке вводится новая конструкция – цикл n раз. Это конструкция повторения, позволяющая с помощью короткой записи выполнить длинную последовательность команд. Зачем это надо? Дело в том, что быстродействие компьютера поистине феноменально: за 1 секунду процессор может выполнить миллион команд. Поэтому в языках программирования широко используются конструкции, позволяющие максимально сократить запись программ (алгоритмов). Иначе с программами будет крайне неудобно работать – составлять, оптимизировать, отлаживать. Синтаксически конструкция цикл n раз – составная. Она начинается служебным словом нц с указанием числа повторений, а заканчивается служебным словом кц. Нетрудно догадаться, что указанные служебные слова задают рамки цикла – его начало и конец. Последовательность команд для повторения (тело цикла) записывается между словами нц и кц со сдвигом вправо – чтобы была хорошо видна структура конструкции.

Понятно, что тело цикла может содержать любые команды, в том числе – вспомогательные алгоритмы и другие циклы. Цикл внутри цикла называется вложенным циклом. Теоретически вложенность может быть любой глубины. На листе определений приводятся алгоритмы с несколькими циклами и с вложенным циклом. Для того чтобы продемонстрировать детям, насколько циклы упрощают запись алгоритма, можете попросить их в качестве домашнего задания переписать какой-нибудь алгоритм с листа определений, заменив его простой последовательностью команд.

Число повторений в цикле может быть любым целым числом, в том числе нулем или отрицательным числом. В последних двух случаях цикл не будет выполняться ни одного раза.

Задача 66. Закрепление материала листа определений. Здесь предлагается использовать приведенный на листе определений вспомогательный алгоритм закрасить ряд из 10 клеток. Обратите внимание учеников на то, что этот вспомогательный алгоритм составлен так, что роботу делает лишний шаг вправо, поэтому в начальных условиях надо указать длину поля на 1 клетку больше. Несмотря на то что при составлении алгоритма ребята будут использовать один и тот же вспомогательный алгоритм, решения у них могут получиться разные. Вот примеры двух рациональных алгоритмов:

Задача 67.

Простая задача на закрепление нового материала. Для ответа на первый вопрос можно подсчитать количество выполненных команд закрасить по алгоритму: (3 + 3 + 2 · 2) ∙ 5 = 50 раз.  Или можно нарисовать результат выполнения одного (большого, внешнего) цикла и сосчитать, сколько раз Робот выполнил команду закрасить, учитывая, что одну клетку Робот закрасил дважды:

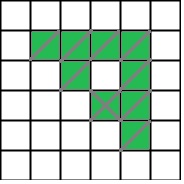
Поскольку этот цикл будет выполнен Роботом пять раз, остается умножить полученный результат (10 клеток) на 5.

Для ответа на второй и третий вопросы нужно аккуратно нарисовать результат выполнения всех пяти циклов, как-то помечая, сколько раз Робот раскрашивал клетку, или хотя бы различая ситуации «раскрашена один раз» и «раскрашена больше раз». Например, можно перечеркивать клетку по диагонали один раз при первой раскраске и по другой диагонали – при каждой повторной раскраске.

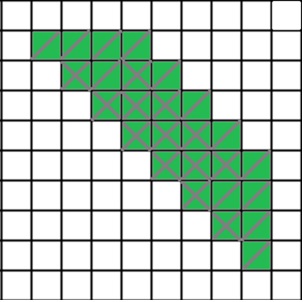
По получившемуся рисунку будет нетрудно ответить на второй и третий вопросы: всего будет 26 закрашенных клеток, из них по одному разу – 13 клеток.

Задача 68. Необязательная. Задача средней сложности на смекалку. Из 79 мест 9 мест занимают однозначные числа. Отбросим их – остается 70 мест. Переформулируем вопрос задачи: какая цифра будет на 70-м месте? Ясно, что на 70 местах поместятся 35 двузначных чисел, начиная с 10. Первые 30 чисел – это числа 1-го, 2-го и 3-го десятков. На последних пяти местах будут: 40, 41, 42, 43, 44. Последняя цифра – 4, это и есть ответ к задаче.

Задача 69. Простая задача, которая поможет учащимся лучше вникнуть в смысл конструкции цикл n раз и оценить ее полезность.

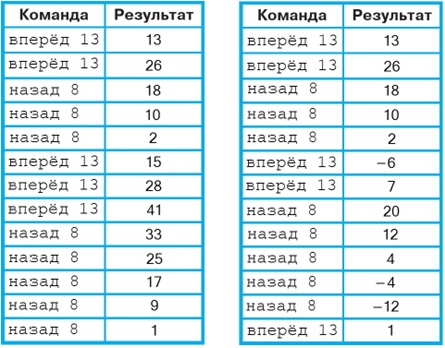
Задача 70. Необязательная. По сути, это арифметический ребус. Здесь всего лишь необходимо подобрать два произведения (одно – кратное 8, другое – кратное 13), разность между которыми равна 1. Это числа 40 и 39. То  есть в искомом алгоритме команда назад 8 должна быть повторена 5 раз, а вперед 13 – 3 раза.

В условии задачи сказано, что Кузнечик не удаляется от начального положения (от точки 0) больше чем на 50 шагов. Следовательно, мы можем перемещать Кузнечика от точки – 50  до точки 50. А для того чтобы в результате выполнения алгоритма Кузнечик переместился на один шаг вправо, необходимо, чтобы в процессе «прыжков» он оказался в одной из следующих точек: – 38; – 25; – 12; 9; 17; 25; 33; 41; 49. Задача не имеет единственного решения, алгоритмы у ребят могут быть различными. Вот примеры двух рациональных алгоритмов:

Задача 71. Необязательная. Простая задача на повторение операций над множествами, требующая аккуратности и внимания. Но здесь есть маленький нюанс. Последнее задание (пересечение всех трех множеств) можно, конечно, искать «в лоб», а можно воспользоваться результатами предыдущих заданий. Для этого достаточно найти пересечение двух предварительно найденных пересечений – А и Б и Б и В (пункты задачи а) и в)). Попросите тех детей, которые до этого додумаются, объяснить свое решение.

Задача 72. Отработка новой конструкции цикл n раз. Чтобы выяснить количество повторений, достаточно 360 разделить на 3.

Задача 73. Задача, аналогичная предыдущей, но с небольшим отличием. Здесь надо строить алгоритм по-другому: фактически, надо повторить 100 раз некий вспомогательный алгоритм, переводящий Кузнечика на 1 шаг вперед, т.е. пару команд вперед 3, назад 2. Возможно, кому-то будет сложно понять, сколько нужно повторений. Если ученик ошибся, спросите его, сколько потребуется повторений, чтобы Кузнечик из точки 0 попал в точку 1. Ясно: одно. А в точку 2? Понятно: 2. Так каково же правило? Число повторений равно значению точки, т.е. 100.

Задача 74. Довольно сложная задача, требующая внимания и аккуратности. Чтобы использовать циклы, ребенку надо, прежде всего, вычленить повторяющиеся участки узора. Это можно сделать по-разному. Соответственно, и алгоритмы у детей могут оказаться разными. Важно, чтобы там были циклы и вложенные циклы. И, конечно, чтобы, выполняя алгоритм, Робот рисовал именно тот рисунок, который дан в условии. В остальном ребенку предоставляется полная свобода. Никаких требований к эффективности алгоритма мы не предъявляем. Если есть такая возможность, хорошо бы после решения устроить парную проверку.

Задача 75. Продолжение задачи 74. Заметим, что использование вспомогательных алгоритмов вовсе не отменяет возможности использования циклов. Наоборот, такое решение будет только приветствоваться. И, опять же, вспомогательные алгоритмы, которые напишут ребята, могут быть разными.

Задача 76. Это сюжетная математическая задача, однако строгих математических методов ее решения дети еще не знают: для этого необходимо уметь решать уравнения в целых числах. Но и наши информатические методы при решении этой задачи могут быть весьма результативны. Особенно эффективным здесь будет метод перебора. Конечно, сильные дети проведут необходимый перебор без всякого дерева, в уме. Однако многим детям будет полезно все-таки построить дерево перебора, только надо разобраться, как это лучше сделать. В данном случае количество возможных порций мороженого и количество шоколадок жестко связаны суммой наличных денег. Поэтому мы не можем перебирать их независимо друг от друга. Значит, перебор нужно вести только по количеству одного из продуктов, количество другого продукта получится автоматически из общей суммы имеющихся рублей. Допустим, мы будем вести перебор по числу шоколадок. Ясно, что это число может быть равно 0 (если Оля вообще не покупала шоколадок), 1, 2 и т. д. Нарисуем дерево, в котором корневыми вершинами будут возможные стоимости шоколадок в Олиной покупке. Конечно, эта стоимость не должна превышать 102 р. (иначе денег Оле не хватит даже на шоколадки). Чтобы дерево было более наглядным, можно на каждом ребре, идущем от корня, написать соответствующее число шоколадок в Олиной покупке. Получается следующий вид первого уровня вершин:

Теперь для каждого числа шоколадок подберем такое наибольшее число

порций мороженого, чтобы на покупку хватило 102 рублей. Стоимость такой

покупки запишем около стрелки. Получаем следующее дерево перебора таких вариантов покупок шоколадок и мороженного, чтобы на сдачу невозможно было уже купить ни шоколадки, ни мороженого.

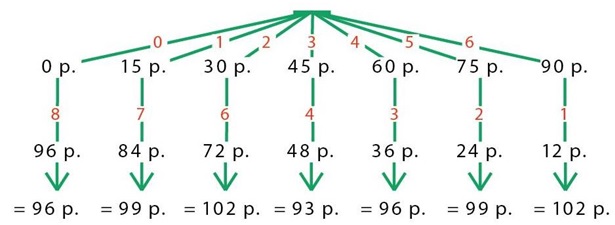
Теперь найдем в дереве все пути, напротив листа которых стоит сумма 102 р. – это будут покупки без сдачи, которые нам нужны.

Ответ: Оля может купить 2 шоколадки и 6 порций мороженого или 6 шоколадок и 1 мороженое.

Задача 77. Закрепление материала листа определений. Первое задание не представляет никаких трудностей, а вот второе потребует некоторой смекалки. Попробовав беспорядочный перебор, большинство детей догадаются решать задачу с конца, т.е. производить действия, обратные тем, которые должны выполняться по алгоритму: делить результат на 2 и вычитать 1. Накопив некоторый опыт, дети поймут, что для того чтобы добиться максимальной эффективности (максимально укоротить алгоритм), четный результат надо делить на 2, а от нечетного отнимать 1.

Задача 78. Необязательная. 

Ответ: площадь многоугольника Ф 12 ед. кв.

Задача 79. Необязательная. Сложная задача  на сообразительность. Прежде всего, надо уяснить себе зависимость между числом распилов одного бревна и числом получившихся после этого поленьев. Попросите детей нарисовать схематично бревна, распиленные на 2, 3, 4, 5 частей. Мы можем легко убедиться, что распилов (для одного бревна) всегда будет меньше на 1, чем поленьев. То есть если при распиле одного бревна получилось 2 полена, то был 1 распил; если поленьев 3, то распилов – 2, если поленьев 4, то распилов – 3, и т.д. По условию задачи получили 72 полена, сделав 52 распила. То есть распилов было на 20 меньше, чем полученных поленьев (72 – 52 = 20). Следовательно, и брёвен было 20.

Задача 80. Построение дерева перебора вариантов. Поскольку команд не больше пяти, уровней в дереве будет 6 (включая начало). Из каждого элемента будет выходить по 2 ребра – по числу возможных команд. При этом одну из ветвей дерева можно не рисовать, т.к. уже на втором уровне мы получим два одинаковых элемента – 2. Значит, одна из ветвей дерева будет повторять другую (с точностью до перестановки элементов одного уровня). Таким образом, достаточно построить фрагмент дерева от любого элемента второго уровня. Ответ: возможны следующие числа: 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 16, 24. Из чисел 2-го десятка здесь нет: 11, 15, 17, 18, 19, 20.

Задача 81. Необязательная. Поиск 3-х одинаковых фигурок. Решается полным перебором. Посоветуйте детям в процессе перебора использовать ту или иную систему, чтобы, с одной стороны, не делать лишнюю работу, а с другой – не пропустить какую-нибудь букву. Ответ: три одинаковые буквы – π. В единственном экземпляре встречается буква α.