Компьютерное дополнение к курсу Информатика 6. 2024

Урок 10. «Поиск кратчайшего пути»

Мы продолжаем знакомить ребят с практическими задачами, которые удобно решать с помощью деревьев. Одна из них – поиск оптимального пути, выбранного по некоторому критерию. Ясно, что один из практических способов решения такой задачи – полный перебор всех путей. Действительно, перебрав все пути и рассмотрев их с точки зрения выбранного критерия, можно найти оптимальный путь непосредственно. Значит, эта задача включает в себя проведение полного перебора, которое мы подробно обсуждали на предыдущем уроке. Что нового содержит данная задача? Во-первых, на этом уроке дети будут работать в основном со взвешенными деревьями, то есть такими, каждому ребру которого присвоено некоторое число (вес). Это позволяет анализировать пути дерева с точки зрения выбранного критерия (чаще всего длины маршрута). Во-вторых, здесь дети впервые знакомятся с понятием графа. Вообще, графы в нашем курсе не входят в число наиболее употребляемых понятий, а играют вспомогательную роль. Мы в наших задачах чаще всего используем лишь один вид графа – деревья, которые обладают определенным набором характеристических свойств (см. урок «Дерево»). В задачах на поиск оптимального пути мы используем графы фактически не для решения задачи, а для ее более краткой формулировки. Действительно, все возможные пути, среди которых в задаче предстоит осуществлять перебор, можно было бы в условии описывать словами, но это было бы слишком долго. Гораздо проще нарисовать картинку, где были бы изображены все пункты следования, все дороги, по которым можно проходить от одного пункта к другому. Если в задаче требуется не просто найти все возможные пути, но и определить оптимальный, то графы, естественно, будут взвешенными, чтобы впоследствии можно было определить вес каждого пути дерева перебора и выбрать путь с наименьшим весом.

Напомним, что наше дерево (в отличие от произвольного графа) всегда направленно, то есть из двух соседних вершин (соединенных общим ребром) всегда лишь одна является следующей по отношению к другой. А другая при этом является предыдущей по отношению к первой, и она, соответственно, расположена ближе к началу (корню) дерева. У произвольного графа это обычно не так – из любой вершины можно двигаться к любой другой в любом направлении, никакого начала и конца у произвольного графа нет. Исходя из сюжета задачи, мы определяем точку начала маршрута и точку конца маршрута, но если граф не направленный, то маршрутов оказывается слишком много. Поэтому часто в задачах мы будем использовать направленные графы – такие, в которых по некоторым ребрам можно двигаться только в одном направлении. Такие ребра мы будем помечать стрелочкой.

Также обращаем внимание, что в рамках решения задачи поиска кратчайшего пути мы не будем рассматривать маршруты с возвращениями, когда по одному ребру графа проходят несколько раз. Даже детям ясно, что такой маршрут не будет кратчайшим. Обычно в условии задач мы будем об этом писать явно, но в любом случае это всегда нужно держать в голове.

Рассмотренный на листе определений пример, по сути, дает детям алгоритм для решения задач на поиск оптимального пути, поэтому необходимо разобрать лист определений тщательно и ответить на все возникающие вопросы.  Например, хорошо бы сразу объяснить ребятам, что граф – это не уменьшенный рисунок, не карта маршрутов, а просто графическая схема. На ней пункты назначения и дороги располагаются не так, как на реальной карте, то есть реальные соотношения длин не отражаются. Граф отражает лишь то, какой пункт с каким соединен дорогой, а длина этой дороги помечена числом. Что касается соотношений длин этих отрезков, они на графе не отражаются, поэтому ребро весом 3 может на графе выглядеть короче, чем ребро весом 1. Иногда ребра графа мы будем изображать прямолинейными отрезками, иногда – криволинейными, это делается только из соображений удобства зрительного восприятия графа. На самом деле это совершенно не важно, повторим, что граф не отражает реальной длины и конфигурации дорог.

 

Задача 59. В этой задаче ребята, по сути, делают то же самое, что они видели на листе определений. Если кто-то из детей не знает, с чего начать,  надо попросить его вернуться к задаче про почтальона. Как и в задаче про почтальона, схема дорог представляет собой взвешенный граф. Вес ребер – длина соответствующей дороги между двумя соседними пунктами (соединенными общим ребром) в километрах. Конечно, между этими задачами есть некоторая разница. В задаче с листа определений почтальон должен был обязательно объехать все населенные пункты (по одному разу) и вернуться на почту, поэтому длина каждого пути дерева перебора была одинаковой. Здесь ситуация другая – Коле надо просто дойти до школы, при этом он может пройти через два пункта, а может – через пять. Заметим, что длина пути дерева никак не связана с длиной Колиного маршрута – длинный путь может соответствовать более короткому маршруту. Именно поэтому мы и строим дерево полного перебора – все критерии, которые на первый взгляд кажутся правдоподобными, могут нас обмануть. Другое отличие данной задачи от задачи про почтальона в том, что мы имеем дело теперь с направленным графом, в котором по некоторым ребрам можно двигаться только в одном направлении. Это существенно уменьшает количество маршрутов и, соответственно, наш перебор. Итак, начинаем мы, конечно, с вершины Д – начала маршрута. Из нее можно попасть в В, А и Б, значит, это дети вершины Д (вершины второго уровня). Теперь разберемся с каждой из них отдельно. Из вершины В можно попасть только в Г, ведь в Д нам возвращаться нельзя (иначе мы дважды пройдем по одной дороге), значит, у В одна следующая вершина – Г. Из Г можно попасть в Ш и А, значит, это дети Г. Видим, что один из маршрутов до школы уже построен, продолжаем второй маршрут (из вершины А). В результате получаем, что из вершины В можно дойти до школы только двумя маршрутами. Затем, аналогично, работаем с вершиной А (там тоже получаем два маршрута) и с вершиной Б (там получается один маршрут). Получаем следующее дерево  полного перебора маршрутов:

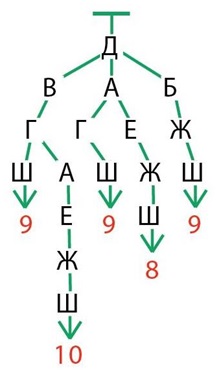
Теперь посчитаем вес каждого пути дерева. Получаем три маршрута длины 9, три маршрута длины 10 и один маршрут длины 8, он и будет самым коротким.

Ответ:  самым коротким оказался маршрут Д – А – Е – Ж – Ш. Длина этого маршрута – 8 км.

Задача 60.  Повторение материала предыдущего урока. Аналогичные задачи ребятам уже встречались. Дерево перебора будет строиться в точности так же, как в задаче 46, а элементы этого дерева можно нарисовать так же, как в задаче 3 с предыдущего листа определений (бусины с пометками «есть», «нет»). Как и в задаче 46, здесь множество имеет ровно 16 подмножеств.

Задача 61. Как мы уже говорили, основной задачей нашего курса является выработка у ребенка информационной культуры. Основным индикатором информационной культуры является успешность решения учащимся встающих перед ним жизненных (практических) и учебных (прикладных) задач. Именно поэтому у нас в учебнике помимо чисто учебных задач столь часто встречаются практические и прикладные задачи, они позволяют детям учиться осуществлять перенос полученных в курсе знаний на новое содержание. Серия таких задач не однородна. Так, почти все задачи этого и предыдущего урока по содержанию являются прикладными и одновременно учебными, поскольку это задачи на новый лист определений. В серии практических и прикладных задач одна из основных разновидностей – задачи на применение деревьев. Действительно, древесная структура характерна для многих реальных процессов и научных моделей. В данной задаче мы показываем детям, что в виде дерева можно представить процесс вычисления арифметического выражения. Классы, которые изучали наш курс в начальной школе, наверняка помнят, что тогда мы выделяли «Дерево вычисления арифметического выражения» в отдельную тему и занимались ею достаточно много. В курсе 5 класса этот вопрос существует в виде одной задачи как пример применения деревьев к процессам в арифметике.

Для тех учителей, которые работают с нашим курсом первый год, кратко повторим особенности дерева вычисления арифметического выражения. Дерево вычисления имеет некоторые отличия от тех деревьев, с которыми ребятам приходилось работать до сих пор. Первое из них в том, что обычно, работая с деревьями (строя их и анализируя), мы двигались от элемента первого уровня к листьям. Здесь же естественный порядок построения и анализа дерева обратный: от листьев к началу. Вторая особенность дерева вычисления – необычность элементов. Действительно, мы привыкли к тому, что элементами дерева могут быть цифры, буквы, бусины, фигурки или последовательности элементов (числа, слова и т.д.). Здесь же листьями являются числа, которые есть в исходном примере, а в остальных элементах должны быть отражены и действия, которые выполняются на некоторой ступени, и результаты этих действий. В начальной школе мы писали в таких бусинах числа-результаты, а действие помечали цветом бусин. Здесь мы сделали иначе, поскольку задача используется как один из примеров применений дерева, ради этого не стоит вводить слишком много новых обозначений. А главное, что эту конкретную задачу в таком дизайне дерева решать, действительно, можно нагляднее. В данном случае результаты отдельных действий находить просто не нужно, как и результат выполнения примера в целом, для шестиклассников вопрос счета и порядка действий уже не столь актуален, как для детей начальной школы. Здесь цель задачи другая – сопоставить объект, организованный по типу последовательности (арифметический пример), с объектом, организованным в виде дерева, причем при этом дети руководствуются известными договоренностями о порядке выполнения действий в примере.

При построении примера по дереву ребенок двигается от листьев к началу. Первыми выполняются действия предпоследнего уровня, дальше – действия предыдущего перед ним и так далее. При этом порядок выполнения действий в соответствии с уровнем дерева дети устанавливают при помощи скобок.

Ответ:

выражение для дерева А: 2·5;

выражение для дерева В: (45:9) · (8+5);

выражение для дерева С: 8 + (71‒33);

выражение для дерева D: ((7·89)+(6+17)) + (15‒8);

выражение для дерева Е: ((21:3) · (4+5)) · ((26‒7)+(8·9)).

Задача 62. Необязательная. Это типичная математическая задача на сообразительность и смекалку, которая может быть решена с помощью наших (информатических) методов. Например, если ребенок не знает, с чего начать, посоветуйте ему построить дерево перебора всех путей от начала до конца по лабиринту. Тогда путей у крысы будет ровно столько, сколько будет путей в нашем дереве перебора. Итак, на первом уровне у нас две вершины – два прохода. После каждого из них – три вершины (по три прохода), значит, на втором уровне дерева будет уже 6 вершин. Наконец, после каждой из этих 6 вершин по 4 следующих вершины, значит, всего в дереве 24 пути (столько же путей у крысы в лабиринте). Заметим, что сильные ученики могут дойти до этого ответа не строя дерева, при помощи рассуждений. С другой стороны, ребенок может просто посмотреть ответ в конце учебника. Поэтому если вы видите, что у ученика в тетради нет ничего кроме ответа, нужно его спросить, как получился этот ответ и как он рассуждал при этом.

Задача 63. Это очень важная задача, поскольку здесь мы начинаем формировать у детей новое умение. До настоящего момента мы учили детей работать с деревьями только непосредственно, то есть либо рассуждать по готовому (построенному нами) дереву, либо строить дерево, а затем по нему работать. Во всех случаях дерево всегда было перед глазами ребенка. Здесь мы впервые учим детей рассуждать по дереву, которое не построено, но его можно представить. Зачем нужно такое умение? Нетрудно убедиться, что наши возможности построения деревьев всегда ограничены чисто техническими параметрами, например такими, как размер листа или время урока. При этом если нам надо лишь ответить на вопрос: «Сколько…», а не выписать пути дерева явно, то большая часть проведенной работы окажется невостребованной. Отвечая на вопрос: «Сколько…», удобно просто представить себе дерево и двигаться от корня, последовательно задавая себе вопрос: «Сколько…», пока мы не дойдем до листьев. Именно так построен образец, по которому мы предлагаем описывать детям нужное дерево. В основном, аналогичные задачи мы будем строить о деревьях, которые имеют некоторые ярко выраженные особенности, которые позволяют не только представить дерево, но и удержать в голове общие принципы его построения, в том числе легко посчитать число вершин на каждом уровне. Чаще всего так получается, если дерево симметрично относительно входящих в него элементов. Поскольку все они входят в дерево равновероятно, то каждая ветка выглядит так же, как соседняя, и ее легко спрогнозировать и обсчитать.

Приведем рассуждения, которые в этой задаче необходимо провести ребенку. Инициалы двухбуквенные, значит, наше дерево будет состоять из двух уровней – на первом будет располагаться первая буква инициалов, на втором – вторая. Первая буква инициалов может быть любой, кроме Ъ и Ь, значит, на первом уровне будет 31 вершина. Первая и вторая буквы инициалов не связаны, для каждой первой буквы вторая снова может быть любой. Значит, у каждой корневой бусины ровно 31 ребенок (все буквы, кроме Ъ и Ь). В результате получаем, что в дереве 31² листьев.

Ответ: в русском языке существует 961 набор двухбуквенных инициалов.

Задача 64. Построение последовательности из элементов множества. Как видно из утверждений задачи, здесь последовательность строится только из элементов данного множества, но эти элементы в последовательности могут повторяться. Чему равна длина искомых последовательностей? Она меньше 4, но не равна одному (поскольку в последовательности есть две одинаковые бусины). Значит, последовательность может иметь длину 2 или 3. Выпишем сначала двухэлементные последовательности. Таких оказывается две – последовательность их двух красных круглых бусин и последовательность из двух красных квадратных бусин. Теперь выпишем все последовательности из трех бусин. Рассмотри сначала все такие последовательности, которые содержат две красные квадратные бусины. При этом третья бусина может быть красной круглой или красной квадратной. В первом случае красная круглая бусина может стоять на каждой из трех позиций в последовательности, значит, таких последовательности будет ровно три. Если третья бусина – красная квадратная, то получается единственная последовательность (из трех красных квадратных бусин). Таким образом, мы построили 4 последовательности, в которых есть две красные квадратные бусины. Аналогично строим 4 последовательности, в которых есть две красные круглые бусины. Всего получается 10 последовательностей, для которых истинны все три данных утверждения. Как видите, в этой задаче очень легко потерять решения. Чтобы этого не случилось, необходимо организовать грамотный перебор – сначала по длине последовательности, а в одной из групп – по виду одинаковых бусин. Если вы видите, что кто-то из ребят потерял часть решения, помогите ему с организацией полного перебора.

Задача 65. Необязательная. Это довольно сложная логическая задача. Ее, конечно, можно решить  методом беспорядочного перебора (методом тыка), но поскольку нам надо по условию доказать, что наше решение единственно верное, то лучше сразу подойти к решению систематически. Итак, три мальчика (Олег, Юра и Миша) стоят в таком порядке: О‒Ю‒М. Рассмотрим последовательно, какие места в цепочке из 5 объектов может занимать эта троица. В принципе таких комбинаций 10:

1‒2‒3           2‒3‒4         3‒4‒5

1‒2‒4           2‒3‒5

1‒2‒5           2‒4‒5

1‒3‒4

1‒3‒5

1‒4‒5

Можно попросить детей построить дерево перебора вариантов. Это процесс не такой простой, необходимо все время оглядываться на порядок следования мальчиков. Например, если Олег стоит на 3-м месте, то Миша не может стоять на 2-м. Удобнее всего на первый уровень поставить все возможные места Олега: 1, 2 и 3. Затем по условию строить дерево, перебирая возможные места для Миши и Юры.

Сразу исключим комбинации: 2‒3‒4, 2‒3‒5 и 2‒4‒5,  потому что на первое место (рядом с Олегом) нельзя поставить ни Сашу, ни Вову. По тем же соображениям исключаем все варианты, где свободно 2-е место: 1‒3‒5 и 1‒3‒4. Также не подходят 1‒2‒3, 1‒4‒5, 1‒2‒5 и 3‒4‒5, т.к. Саша и Вова не могут стоять рядом, а в этих  вариантах свободные места располагаются именно рядом. Остается 1 вариант:

 

1‒2‒3           2‒3‒4         3‒4‒5

1‒2‒4           2‒3‒5

1‒2‒5           2‒4‒5

1‒3‒4

1‒3‒5

1‒4‒5

 

Вариант 1‒2‒4 нам подходит: Сашу ставим на 5-е место, Вову – на 3-е.