Компьютерное дополнение к курсу Информатика 6. 2024

Урок 7. «Вспомогательный алгоритм»

На листе определения наглядно (на примере) разъясняется понятие  вспомогательный алгоритм – это  алгоритм, который можно использовать в других алгоритмах, указав только его имя.

Задача 32. Отработка материала листа определений. Если первая часть задания сводится к длинной цепочке вычислений, то вторая часть потребует от ученика к тому же еще и логических рассуждений. Надеемся, большинство учеников догадаются решать задачу с конца, последовательно производя с требуемым результатом (94) обратные действия. Заметим, что навыки изменения, оптимизации, отладки программ являются для нас важнейшей учебной целью.

Задача 33. Повторение исполнителя Кузнечик. Первая часть задачи наиболее сложная. Можно, конечно, решить ее беспорядочной подстановкой слагаемых (7 со знаком + и 5 со знаком -), однако красивое решение состоит в том, чтобы подобрать два произведения – одно, кратное 7, и второе, кратное 5, при этом разность между первым и вторым должна быть равна 1. Это числа 21 и 20. Ясно, что вперед 7 надо сделать 3 раза, а назад 5 – 4 раза. На второй вопрос задачи ответить совсем несложно, имея в арсенале команду вперед 7 и вспомогательный алгоритм шаг вперед.

Задача 34. Здесь имеется в виду, что с помощью алгоритма шаг вперед из предыдущей задачи составляется новый алгоритм (назовем его 3 шага вперед), который тоже может использоваться как вспомогательный для перемещения на 9 шагов вперед, а этот последний – для перемещения на 15 шагов вперед.

Задача 35. Первая часть задачи имеет несколько решений. Вот самый рациональный (короткий) алгоритм налей в А 1 меру:

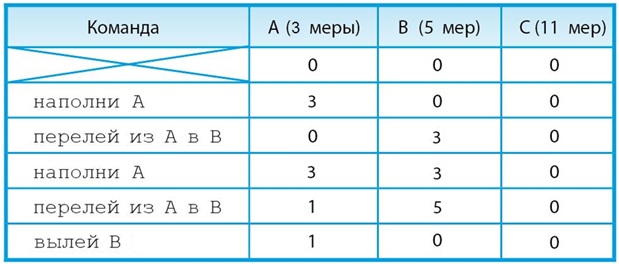
В условии второй части задачи есть ограничение – в алгоритме не может быть более 4 команд. Поэтому решение здесь единственное:

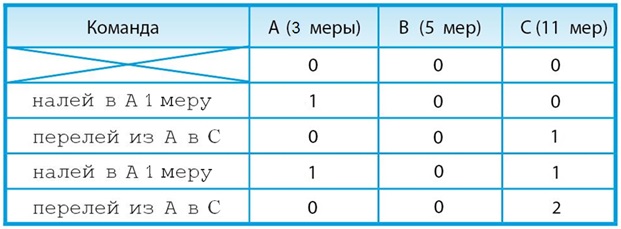
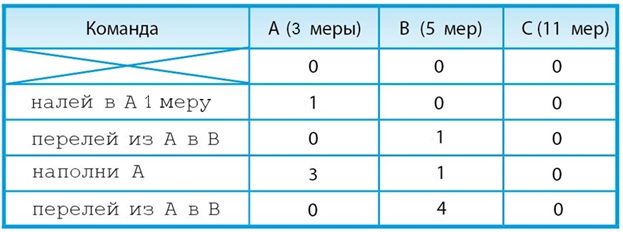
Задача 36. Так же как и во второй части предыдущей задачи 35, здесь нужно составить алгоритм для Водолея, используя вспомогательный алгоритм налей в А 1 меру. При решении этой задачи можно рассуждать так.

а) Нам нужно получить в сосуде В 4 меры воды. По условию задачи одной из четырёх команд составляемого алгоритма будет налей в А 1 меру. Соответственно эту 1 меру воды нужно перелить в сосуд В (это вторая команда). Останется налить в сосуд В ещё 3 меры воды – это вместимость сосуда А.

Ответ:

б) Нам нужно получить в сосуде С 9 мер воды. По условию задачи одной из четырёх команд составляемого алгоритма будет налей в А 1 меру. Так как вместимость сосуда А 3 меры, то в него может поместиться ещё 2 меры воды. Вместимость сосуда С 11 мер. Чтобы получить в нем 9 мер воды, нужно его наполнить и отлить 2 меры в сосуд А.

Ответ:

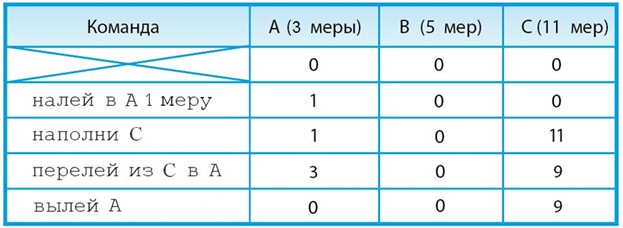
Задача 37. Составление алгоритма для Робота. Внимательно проанализировав рисунок поля Робота, вычленяем в нем 4 повторяющиеся части – прохождение одной такой части и будет обеспечиваться вспомогательным алгоритмом. Еще останется пройти две клетки до конечной точки – итого ровно 6 команд, что и требовалось по условию.

Задача 38. Довольно сложная задача, как по объему работы, так и по содержанию. Прежде всего, надо понять, что получается в результате выполнения вспомогательного алгоритма фрагмент и где оказывается Робот. После этого становится ясно, в каком направлении будут строиться следующие фрагменты и каково оптимальное начальное положение Робота (левый верхний угол). Что же касается комментария в поле дано, то здесь решения могут быть разными – в зависимости от степени точности описания. Например, можно сказать, что для выполнения алгоритма фрагмент должен быть свободен квадрат 4 х 4 клетки, в левом верхнем углу которого находится Робот. А можно потребовать, чтобы свободным был только периметр этого квадрата или даже его часть. Аналогичным образом обстоит дело с алгоритмом фигура – простое описание задает поле целиком в виде квадрата, более сложное описание указывает границы свободных областей более точно. На рисунке показан результат выполнения алгоритма фигура с указанием начального и конечного положения Робота.

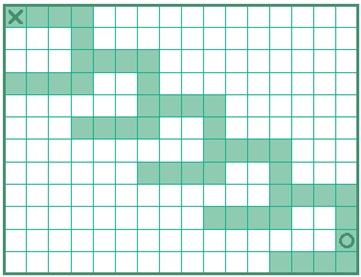
Задача 39.

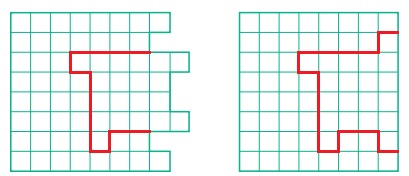
Задача 40. Продолжение задачи 38. Ответ на первый вопрос задачи отыскивается пересчетом команд закрасить в алгоритме фрагмент и умножением этого числа на 5. Для ответа на второй вопрос можно просто посчитать по рисунку общее количество закрашенных клеток и, вычислив разницу, получить ответ. А можно сообразить, что последние 4 фрагмента Робот начинает с команды закрасить, находясь на уже закрашенной клетке. Таким образом, ответ: 4 клетки поля будут закрашены дважды.

Задача 41. Необязательная.

Ответ:

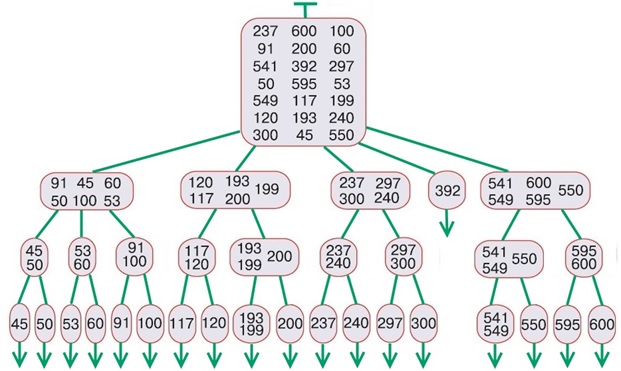
Задача 42. Повторение темы «Дерево сортировки». Задача несложная, но требует внимательности и аккуратности.

Задача 43. Необязательная.

Аналогичную задачу ребята уже решали. Ее стоит предложить тем учащимся, у которых  задача 22 вызвала трудности.

Ответ:

Apple – яблоко

Banana – банан

Fig – инжир

Grape-fruit – грейпфрут

Kiwi fruit – киви

Lemon – лимон

Mandarin – мандарин

Pear – груша

Persimmon – хурма

Pineapple – ананас

Pomegranate – гранат

Quince – айва