Компьютерное дополнение к курсу Информатика 5. 2024

Урок 34. «Выравнивание, решение необязательных и трудных задач»

Задача 203. В данном случае решением будет последовательность, в которой нет одинаковых бусин – все бусины из множества есть в последовательности представлены и при этом по одному разу (это условие записано в третьем утверждении). Два оставшихся утверждения указывают порядок бусин, взятых из множества Р. В нашем распоряжении две квадратные бусины и красных тоже две, причем одна бусина – красная квадратная. Значит, после квадратной красной должна идти красная круглая, а после квадратной зеленой – квадратная красная. Получается следующий фрагмент последовательности:

По условию второго утверждения после каждой красной бусины должна идти круглая. После квадратной красной круглая в нашем фрагменте уже стоит. Нужно поставить круглую бусину и после красной круглой – ставим зеленую круглую. Теперь все условия задачи учтены, при этом место желтой треугольной бусины не определилось однозначно – она может стоять и первой, и последней. Итак, задача имеет ровно два решения.

Задача 204. Аналогичные задачи детям уже встречались. Из условия следует, что здесь важен не только правильный ответ, но и способ решения. Площадь фигуры должна быть найдена не разрезанием, а достраиванием многоугольника П до квадрата. Чтобы найти площадь П, из квадрата 5 на 5 клеток надо вырезать две части.

Ответ: площадь П равна 21 ед. кв.

Задача 205. Аналогичные задачи на построение последовательности по индуктивному описанию детям уже встречались (см. комментарии к задачам 66, 132). Здесь описание требует более тщательного анализа, поскольку оно включает условие типа «Если, то». Конечно, решений в этой задаче много, каждая подходящая последовательность полностью определяется тем, какие два первых члена мы выбрали. Вот пример решения построенного для случая, когда, если первый член – 2, а второй – 3:

2 – 3 – 7 – 42 – 12 – 47 – 282 – 52 – 312

Задача 206. Необязательная. Задача продолжает линию начатую в задачах 162 и 163. Больше того, Решение этой задачи во многом опирается на решение качественных задач об исполнителе Водолей – задач 162 и 163, поэтому предлагайте решать эту задачу только тем ученикам, кто уже решил предыдущие задачи этой линии или по крайней мере познакомился с их решением.

Вместимость всех трех сосудов, данных в пункте а), кратна трем. Поэтому с помощью этих сосудов можно отмерить только количество воды, кратное трем: 1 и 2 мер отмерить не получится, а 3 меры отмерить получится (например, набрать полный сосуд вместимостью 15 и перелить из него 12 в сосуд вместимостью 12 мер – останется 3 меры).

Вместимость всех трех сосудов пункта б) не имеет общего кратного, поэтому скорее всего с помощью этих сосудов можно отмерить любое количество мер. Доказательство этого факта может быть дополнительным заданием для сильных учеников. Но в этой задаче этого не требуется.

Одну меру можно отмерить так: Налить полный сосуд в 15 мер, перелить из него в 10-мерный, потому вылить 10-мерный и снова перелить из 15-мерного в 10-мерный (в нем при этом окажется 5 мер). Теперь наливаем полный 6-мерный сосуд и выливаем из него в 10-мерный – туда поместится только 5 мер, 1 мера останется.

Отмерить 7 мер можно, например, отмерив 1 меру и перелив ее из 6-мерного в 15-мерный сосуд, а потом еще налить полный 6-мерный и долить его в 15-мерный.

Задача 207. Необязательная. Теперь в задачах на поиск площади многоугольника на сетке дети сами выбирают способ решения – разрезание на части или достраивание до прямоугольника. В данном случае оба способа будут иметь практически одинаковую сложность.

Ответ: площадь многоугольника Д равна 11 ½ ед. кв.

Задача 208. Качественная задача об исполнителе Робот, которая является продолжением задачи 188. В отличие от задачи 188, в алгоритме этой задачи есть команды закрасить. Детям, решившим задачу 188 сразу будет ясно, что команды, перемещающие Робота, надо поставить в обратном порядке и при этом заменить каждую из них на противоположную. К позиции команды закрасить в этом новом алгоритме надо подойти аккуратно. Рассмотрим совсем простой алгоритм, из двух команд:

          вверх

          закрасить

Выполняя эту программу, Робот переместится на 1 клетку вверх и раскрасит ту клетку, куда он попал. Выполняя обратный алгоритм, Робот должен закрасить ту клетку, на которой находится, а потом переместиться на 1 клетку вниз. Значит, обратный алгоритм будет таким:

          закрасить

          вниз

Мы поменяли порядок команд и команду вниз заменили на противоположную – команду вниз. Итак, мы получили такой ответ:

Ответ: Толя должен поставить все команды алгоритма в обратном порядке, при этом команды закрасить должны остаться такими же, а остальные команды надо поменять на противоположные.

Задача 209. Необязательная. Решая задачу 195, дети уяснили для себя, что, если Робот не делает петель на своем пути, то в ходе выполнения алгоритма он закрашивает столько клеток, сколько серий из команд закрасить есть в алгоритме. Раз при выполнении исходного алгоритма Робот закрасил 5 клеток, значит, в алгоритме было 5 серий команд закрасить. Сколько именно команд при этом – неизвестно, но их могло быть любое число.

а) Выполняя новый алгоритм, Робот не может не закрасить ни одно клетки, потому что по крайней мере одна серия команд закрасить в новом алгоритме должна быть.

б) В алгоритме было 5 серий команд закрасить. Перестановкой только двух команд в алгоритме невозможно все эти серии собрать в одну. Значит, закрасить только 1 клетку Робот не сможет.

в) Гоша мог, например, поменять местами любые две команды закрасить, при этом алгоритм не изменился и выполняя новый алгоритм, Робот будет по-прежнему закрашивать 5 клеток.

г) Гоша мог, например, поменять одну непоследнюю в серии команду закрасить и одну команду другого типа, которая стояла не вплотную к другой серии команд закрасить. В таком случае появятся две новых серии команд закрасить: одна серия оказалась разбита на две части командой другого вида, а вторая – поставленная на новое место одиночная команда закрасить. Таким образом, в алгоритме стало 7 серий команд закрасить, и Робот будет закрашивать 7 клеток. Этот вариант годится не для каждого изначального алгоритма, но, отвечая на вопрос «Может ли…» мы отвечаем «Да, может».

д) Нет, одной заменой команд не получится сделать из 5 серий закрасить команд сразу 100 серий, даже если самих команд закрасить в алгоритме будет 100.

Задача 210. Необязательная. Это сложная задача. Из четвертого утверждения и условия, что всего в последовательности 10 бусин, следует, что последовательность составлена только из бусин множества Р, взятых по одному разу. Добиться выполнения трех оставшихся утверждений непросто. Упрощает задачу только одно – подходящих решений в этой задаче довольно много.

Из первого утверждения следует, что после каждой квадратной должна идти красная. В множестве Р три квадратные бусины и красных бусин тоже три, причем одна из них квадратная. Значит, после одной квадратной не красной должна стоять квадратная красная, после которой тоже красная. Получаем, например, такой фрагмент:

После оставшейся квадратной бусины тоже должна идти красная, поэтому в искомой последовательности должен где-то встречаться и такой фрагмент:

Используя второе утверждение, к каждому построенному нами фрагменту добавляем справа одну желтую бусину из мешка Р. Получатся два таких фрагмента:

Чтобы выполнялось третье утверждение, справа после каждого фрагмента надо поставить зеленую бусину. Мы можем соедини два наших фрагмента, при этом после желтой бусины первого фрагмента встанет зеленая бусина. В конце полученного фрагмента ставим еще одну зеленую бусину. Затем к получившейся последовательности добавляем оставшиеся в множестве две бусины – в начало или в конец, не важно.

Ответ: вот одна из подходящих последовательностей:

Задача 211. Дети в данный момент должны понимать, что прямоугольный треугольник площадью 12 ед. кв. – это половина прямоугольника площадью 24 ед. кв. Значит, для решения задачи надо найти четыре разных прямоугольника площадью 24 ед. кв. каждый: 1×24; 2×12; 3×8; 4×6. Строим четыре этих прямоугольника и дели каждой пополам диагональю – получаем 4 нужных треугольника.

Задача 212. Стандартная задача на повторение понятия подмножество. Поскольку здесь необходимо построить все подмножества, то так или иначе придется провести полный перебор подмножеств. Если вы видите, что учащийся выписал не все подмножества, натолкните его на идею перебора, можно использовать следующие вопросы. Сколько элементов может быть в искомых подмножествах? (Ответ: 0; 1; 2; 3). Сколько можно построить подмножеств, в которых 0 элементов (или 3 элемента)? (Ответ: одно). Сколько можно построить подмножеств, в которых два элемента (или 1 элемент)? Как их нужно перебирать, чтобы выписать все такие подмножества?

Наибольшие проблемы, по всей видимости, будут с перебором всех двухэлементных подмножеств. Здесь рассуждения могут быть такими. Возьмем одну бусину множества W, например, желтую круглую и найдем все двух элементные подмножества с желтой круглой бусиной. Их два – с красной квадратной и с зеленой квадратной. Теперь найдем все двухэлементные подмножества без желтой круглой бусины. Такое подмножество одно. Значит всего двухэлементных подмножеств три.

Всего получится 8 разных подмножеств множества W.

Задача 213. Необязательная. Задача продолжает линию задач об инвариантах в алгоритме для Робота, возвращающем его в ту же позицию, с которой он начал движение. Это задачи 196 – 198 и необязательная задача 194. Решив эти задачи, дети уже хорошо понимают, что если алгоритм привел Робота в начальную точку, то команд вверх в нем столько же, сколько команд вниз, а команд вправо – столько же, сколько команд влево. И наоборот: если в алгоритме соблюдаются эти правила, то в результате его выполнения Робот вернется в исходное положение.

Поменяв местами команды в алгоритме Ани, Соня не изменила соотношение команд: в новом алгоритме, как и в старом, команд вверх столько же, сколько команд вниз, а команд вправо – столько же, сколько команд влево. Значит, алгоритм Сони тоже приведет Робота в исходное положение.

Задача 214. Необязательная. Задача продолжает линию задач 195 и 210. В отличие от задачи 210, здесь меняют местами два соседние команды.

Итак, есть программа, в которой 5 серий команд закрасить и мы меняем две соседние команды. Какие есть варианты?

1. Меняем местами две подряд идущие команды  закрасить – получаем точно такой же алгоритм. Примеры (в примерах даются только фрагменты алгоритмов, красным обозначены команды, которые меняем местами):

                        вверх

                        закрасить

                        закрасить

                        вправо

2. Меняем команду закрасить и другую команду (не закрасить) и этим отделяем команду закрасить от серии из нескольких таких команд в отдельную серию – получаем алгоритм, который закрашивает 6 клеток. Пример:

                        вверх

                        вверх

                        закрасить

                        закрасить

                        вправо

3. Меняем команду закрасить и другую команду (не закрасить) и эти присоединяем отдельную команду закрасить к другой серии команд закрасить – этим сокращаем общее количество серий команд  закрасить – теперь их становится 4. Пример:

                        вправо

                        закрасить

                        вверх

                        закрасить

                        закрасить

4. Меняем команду закрасить и другую команду (не закрасить) и этим команду закрасить отсоединяем от одной серии  и присоединяем к другой – количество серий команд закрасить не меняется, остается равным 5.

                        вправо

                        закрасить

                        вверх

                        закрасить

                        закрасить

Мы рассмотрели все возможные случаи, других нет. Теперь ответить на вопросы задачи нетрудно.

Ответ: а) не может; б) может – это вариант 3; г) может – это варианты 1 или 4; д) может – это вариант 6; д) не может.

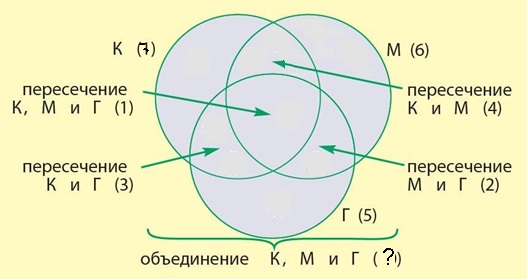
Задача 215. Арифметическая задача об операциях над множествами. Подобные задачи дети уже решали. Отличие данной задачи состоит в том, что здесь имеются не два, а три множества: любителей гороха, любителей моркови и любителей капусты. Действовать здесь учащимся можно по знакомому алгоритму – нарисовать схему с тремя пересекающимися множествами, распределить детей по множествам и их пересечениям в соответствии с условием задачи, а затем найти ответ на вопрос на своей схеме. В нашем случае требуется найти, сколько человек получается в объединении всех трех множеств.

Рисуем схему и помещаем в нее все данные, известные из условия задачи:

капусту любят семеро – пишем 7 около имени множества К;

морковь любят шестеро – пишем 6 около имени М;

горох любят пятеро – пишем 5 около имени Г;

капусту и морковь любят четверо – можно было бы нарисовать 4 кружка в пересечении множеств К и М, но пока не ясно, не надо ли какие-то кружки поместить в ту часть пересечения, которая является пересечением всех трех множеств, поэтому пока напишем 4 около имени «пересечение К и М»;

и так далее – вносим все данные из задачи на схему, получаем такой результат:

Постараемся теперь нарисовать кружки (которые обозначают детей) так, чтобы все данные из задачи были учтены. Уверенно нарисовать кружки мы можем только для пересечение трех множеств, потому что про остальные множества и части мы пока не знаем, как именно распределены в них дети, а пересечение всех трех множеств ни на какие части не разделено и нам известно, что там ровно 1 элемент. Рисуем там черный кружок (или просто жирную точку). Теперь мы имеем возможность нарисовать кружки и в попарных пересечениях (учитывая при этом тот первый кружок, который лежит в пересечении всех трех множеств.

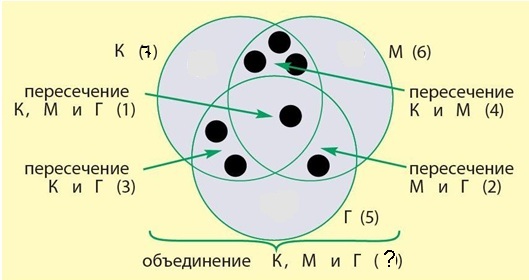
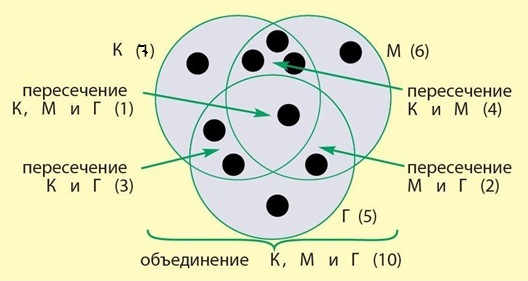
Теперь можем нарисовать кружки в остальных частях множеств и после этого считать общее число детей в семье.

Ответ: в семье 10 детей.

Задача 216. Необязательная. Чтобы ответить на вопросы задачи, надо поэкспериментировать. Будем давать Кузнечику команды по очереди:

          вперёд 7

          назад 5

          вперёд 7

          назад 5

          вперёд 7

          назад 5

Посмотрим, в какие точки числовой прямой они будет при этом  попадать: 7, 2, 9, 4, 11, 6, и так далее: каждый раз, выполняя команду вперёд 7, Кузнечик попадает в нечетную точку, а выполняя команду назад 5, попадает в четную точку. При этом Кузнечик попадает последовательно в каждую точку, начиная с 6 (и еще в точки 2 и 4, но это неважно).

Но нам бы надо попасть в точки –1, 0, 1. Для этого заставим Кузнечика сначала отпрыгнуть назад (выполнить команду ), а потом уже выполнять наш команды попеременно:

          назад 5

          вперёд 7

          назад 5

          вперёд 7

          назад 5

          вперёд 7

          назад 5

          вперёд 7

В этом случае Кузнечик попадет в такие точки: –5, 2, –3, 4, –1, 6, 1, 8, 3, 10, 5… Итак, как попасть в точки –1 и 1 мы теперь знаем. Кузнечик попадает в каждую точку числовой прямой, начиная с 1.

Таким образом, мы нашли такой общий способ попасть в любую точку числовой прямой: для этого надо «допрыгать» вперед или назад так, чтобы попасть в какую-нибудь точку числовой прямой, которая находится не меньше чем на 6 левее нужной точки. И после этого надо начать выполнять команды попеременно: при этом Кузнечик обязательно попадет в нужную точку.

Задача 217. Необязательная. В этой задаче в системе команд Кузнечика параметры кратны 3. Есть подозрение, что это не даст возможности попасть Кузнечику в любую точку числовой прямой, а он будет перемещаться только по числам, кратным 3. Проверим это. Попробуем перемещать Кузнечика вперед или назад. Видим, что Кузнечик, выполнив две команды назад 3 и одну команду вперёд 6 делает «петлю» – возвращается в ту точку, откуда начал. Таким образом, из любого алгоритма можно удалять такие тройки команд (в любой последовательности и из любых мест алгоритма):

          вперёд 6

          назад 3

          назад 3

– и при этом результат выполнения алгоритма не изменится. Сокращая любой алгоритм таким образом, в результате получим алгоритм, который либо составлен из одинаковых команд (или только команды вперёд 6, или только команды назад 3) либо из нескольких команд вперёд 6 и одной команды назад 3. С помощью таких алгоритмов можно попасть только в точки, кратные 3.

Значит, какой бы мы алгоритм не составили, результат его выполнения будет таким же, как результат выполнения алгоритма из одинаковых команд или алгоритма из нескольких команд вперёд 6 и одной команды назад 3 – Кузнечик обязательно попадет в точку, кратную 3. Добраться до точки 1 Кузнечик не сможет.

Задача 218. Задача на повторение темы «Одинаковые мешки», рассчитанная на среднего ученика. Здесь решение можно найти самыми разными путями. Для того, чтобы найти два нужных мешка, сначала ищем мешки, одинаковые по составу фигурок, не принимая во внимание раскраску. Делать это можно разными способами: хаотичным просматриванием или составлением таблицы, в которой в именах столбцов будут стоять все возможные элементы данных множеств, а в именах строк – имена данных множеств.  Таким образом, каждому множеству будет соответствовать строка в таблице – последовательность 0 и 1 (можно назвать ее числом, а можно вектором). И одинаковым множествам будут соответствовать одинаковые строки.

Также при решении этой задачи могут пригодиться все приемы, которые мы использовали при поиске двух одинаковых множеств. Например, можно делить мешки на группы по наличию или отсутствию фигурок. Например, рассмотрим все множества относительно наличия в них сливы. Слива есть лишь в двух множествах (Г и И), но эти мешки разные, можно их отбросить. Теперь рассмотрим оставшиеся множества относительно наличия в них, например, лимона. Лимон есть лишь в двух из них (Б и Ж), причем они разные, значит, их тоже можно отбросить. Теперь осталось 5 множеств, в трех из них есть банан (А, В, Д) , а в двух его нет (З и Е). Сравним множества в каждой из этих групп. Заметим, что множества А и В состоят из одних и тех же фигурок, но луковица в множестве А синяя, а в множестве В – желтая. Значит, эти множества нельзя сделать одинаковыми. Решение отыскивается во второй группе множеств.

Ответ: в множестве Е надо раскрасить яблоко зеленым, в множестве З надо раскрасить луковицу синим.