Компьютерное дополнение к курсу Информатика 5. 2024

Уроки 29–30. «Алгоритм. Ошибки в алгоритмах»

Алгоритм

На этом уроке ученики начинают знакомиться с Алгоритмическим Языком – учебным языком программирования. Этот язык был придуман во второй половине 80-х годов XX века группой отечественных ученых во главе с академиком Андреем Петровичем Ершовым.  Это – универсальный язык программирования. Работая с ним, ученики могут познакомиться с основными конструкциями подобных языков – ветвлениями, циклами (повторениям), вспомогательными алгоритмами (подпрограммами). В курсе 5-го класса мы познакомимся только с простыми линейными алгоритмами, более сложные конструкции будут представлены в курсе 6 класса и в старшей школе.

Важную роль в процессе обучения будет играть практическая работа в системе программирования  Кумир. Эта система разработана в НИИ системных исследований РАН, руководитель проекта – А. Г. Кушниренко. Система Кумир и Алгоритмический Язык имеют ряд особенностей, важных для преподавания информатики.

1. Синтаксис Алгоритмического Языка основан на русском языке. Это особенно важно для преподавания в 5 – 6-х классах.

2. Алгоритмический Язык и система Кумир поддерживают работу с виртуальными исполнителями – как с уже знакомыми вам Водолеем, Кузнечиком и Роботом, так и другими; список таких исполнителей постоянно расширяется.

3. В системе Кумир удобно организована выдача сообщений об ошибках – в отличие от профессиональных систем, сообщение размещается на экране непосредственно рядом с местом ошибки.

4. Предусмотрен специальный режим выполнения («по шагам»), при котором ученик может следить за ходом выполнения программы, отслеживая результат каждого шага.

5.  В системе есть практикумы, которые позволяют каждому ученику индивидуально работать в своем темпе и облегчают учителю контроль работы ученика.

Подробнее о системе Кумир можно узнать в поставляемых вместе с системой справочных материалах.

Ошибки в алгоритмах

К сожалению, сразу написать программу без ошибок получается очень редко. В современном программировании разработаны и разрабатываются специальные приемы, позволяющие уменьшить количество ошибок при написании программ и облегчить обнаружение ошибок. Ученики должны понять, что мало написать программу, про которую они думают, что программа работает правильно. Нужно убедиться, что программа работает правильно. Эта мысль кажется простой, но вам, возможно, придется возвращаться к ней снова и снова.

В реальном программировании, когда создаются комплексы программ, содержащие сотни тысяч команд, разработаны специальные методики тестирования, то есть проверки правильности работы программы на специально подобранных и реальных примерах – тестах. Такая проверка не гарантирует правильности работы программы во всех случаях: точно так же разбор примеров не является заменой доказательству теоремы. Однако, если примеры для тестирования подобраны хорошо и опытная эксплуатация проводилась достаточно долго (месяцы, иногда – годы) и тщательно, то программы на практике работают достаточно надежно.

Так как программа (алгоритм) – это текст, написанный на формальном языке, то можно ставить вопрос и о доказательстве правильности программ. К сожалению, сейчас на практике это возможно только для относительно небольших программ и основным методом, позволяющим убедиться в правильности работы программы и найти ошибки, все-таки является тестирование.

Важно понимать, что нельзя говорить о правильности программы, если мы четко не сформулировали, что она должна делать. Начиная с первых уроков по программированию, мы советуем вам уделять особое внимание описанию исходных данных программы (поля после слова дано) и требований к результатам программы (поля после слова надо).  Эти идеи должны проходить «фоном» через все занятия, ученики постепенно будут осваивать их в ходе занятий. В курсе основной школы ученик должен также освоить идею тестирования, научиться составлять наборы тестов для учебных программ. Он должен понимать, что отладка (поиск ошибок) является такой же неотъемлемой частью программирования, как и придумывание алгоритма и его запись на алгоритмическом языке.

Синтаксические ошибки

Языки программирования (в том числе и Алгоритмический Язык) – формальные языки. Их синтаксис (правила записи алгоритмов) строго определен. В отличие от естественных языков, нельзя заменить слово синонимом, изменить порядок слов и т. п.

К счастью, современные системы программирования (точнее их специальные компоненты – синтаксические анализаторы) распознают синтаксические ошибки и сообщают о них программисту. Система Кумир, которой мы рекомендуем пользоваться при обучении, проверяет отсутствие ошибок в программе после каждого изменения строки программы. При этом не только подчеркивается место ошибки, но и сообщается, в чем она состоит. В сложных случаях система может «не понять», в чем именно состоит ошибка, но в нашем курсе такие ситуации маловероятны.

Таким образом, в результате обучения ученик должен:

Содержательные ошибки

Повторим: синтаксически правильная программа не обязательно делает то, что мы хотим, то есть, не ее поведение не обязательно следует описаниям дано – надо. В программах, которые будут встречаться в нашем курсе, при конкретных входных данных будет легко убедиться, соответствует ли результат тому, что нам нужно. Например, в задачах про Водолея видно, получено ли в одном из сосудов нужное количество воды.  Более того, часто в условии задачи явно указан набор входных данных (например, размеры сосудов Водолея и начальное количество воды в каждом из сосудов), при котором нас интересует работа программы.

В реальной жизни (например, если нам нужно решить довольно сложное уравнение) понять, является ли результат работы правильным, бывает трудно. Это одна из причин, почему необходимо тщательное тестирование программ.

Таким образом, в результате обучения ученик должен:

Замечание. Отладка программы, по сути, представляет собой экспериментальную работу по ее изучению. С таким видом работы дети практически не встречаются в школе (хотя на ранних этапах жизни каждый ребенок много экспериментирует).  Поэтому, особенно в начале сама идея проверки правильности работы программы и анализа результатов этой проверки может вызвать трудности у некоторых детей.

Задача 191. Простая задача об исполнителе Робот. В задаче описывается способ записи решения подобных задач – когда Робот идет по бесконечному (очень большому) полю без внутренних стен и важно только то, как Робот перемещается и какие клетки он при этом закрашивает. Описанный упрощенный способ записи поможет тратить меньше времени на оформление решения в обычно тетради. Также в этой задачи дети закрепляют формат записи алгоритма – они должны сами придумать и записать имя алгоритма, заполнить поля дано и надо.

Задача 192. Задача продолжает работу с алгоритмами, данными в задаче 191. Исправление и модификация алгоритма – важная часть работы по поиску и исправлению ошибок. Мы надеемся, что к этому моменту большинство ваших учащихся уже освоилось с системой команд Робота и эта задача не покажется им трудной.

Задача 193. В задаче вводится новый исполнитель Квадратор. Его система команд похожа на систему команд уже хорошо знакомого детям исполнителя Удвоитель, поэтому  мы сочли возможным сделать эту задачу обязательной. Если по какой-то причине дети в вашем классе еще не знакомы с возведением числа в квадрат, достаточно объяснить им, что это означает просто умножение числа на себя.

Чтобы получить число 5, нужно два раза прибавить по 1, возвести полученное число 2 в квадрат, и добавить еще раз единицу (в минимальной программе будет 4 команды). Чтобы получить число 12, нужно использовать квадрат тройки (в минимальной программе будет 12 команд). Число 25 можно получить возведением в квадрат 2 и потом 5 (в минимальной программе будет 5 команд).

Задача 194. Необязательная. При решении этой задачи ребенку придется самостоятельно найти подходящий инвариант. Вся необходимая подготовка для этого уже проведения в предыдущих задачах о Роботе. Задача предназначена для сильных учеников: мы хотим дать им возможность сделать открытие самостоятельно. Большинству детей это будет сделать сейчас затруднительно – им эту задачу лучше пропустить и прийти к этому выводу постепенно, решая следующие, более простые, задачи.

Чтобы попасть из клетки А в клетку Б, Роботу надо сдвинуться на одну клетку влево и одну клетку вниз – таким образом, алгоритм из двух команд будет минимальным для решения этой задачи. Мы ответили на вопрос пункта а).

Но можно составить и более длинные алгоритмы. Удлинить алгоритм можно, например, за счет «петель»: Робот сдвигается куда-то в сторону от минимального маршрута, а потом тем же путем возвращается в то же точку. В такой «петле» Робот выполнит четное число команд. Таким образом, мы ответили на вопрос пункта б): алгоритм в этом случае будет равным минимальному с добавлением в любое место алгоритма пары противоположных команд, например, влево и вправо.

А что, если Робот в «петле» вернется не тем же путем? Будет ли число команд для выполнения «петли» четным в любом случае? Здесь надо попробовать разные варианты – порисовать разные «пели», сосчитать в них шаги. И после этого сделать очень важный и непростой вывод: для того, чтобы Робот вернулся в ту же точку, число команд вверх в алгоритме должно быть равным числу команд вниз, а число команд влево должно быть равным числу команд вправо. Действительно, если, совершая «петлю», Робот удалился от начальной точки на n шагов по горизонтали, то чтобы вернуться, ему необходимо будет сделать столько же шагов по горизонтали в обратном направлении. И то же самое можно сказать о сдвиге по вертикали. Таким образом, в любое «петле» будет  четное число шагов и соответственно в алгоритм будет добавлено четное число команд. Теперь мы можем ответить на вопрос пункта г) – да, для этого достаточно, например, 1006 раз повторить петлю из одной пары противоположных шагов, например вверх и вниз, а потом выполнить минимальный алгоритм. Или годится любая «петля» из 2012 команд + минимальный алгоритм.

Но вернемся к задаче. Ответить на вопрос пункта в) не так просто: в процессе выполнения алгоритма Робот может пойти «кружным путем» и вообще не следовать минимальному пути, не делать замкнутой петли. Может ли в этом случае в алгоритме получиться нечетное число команд? Здесь пригодятся рассуждения об общем число команд для сдвига по вертикали и по горизонтали. Для перемещения из клетки А в клетку Б Роботу по вертикали надо сместиться на 1 клетку вниз. Это означает, что число команд вниз в алгоритме должно быть на 1 больше числа команд вверх, т. е. число команд, касающихся перемещению по вертикали должно быть нечетным в любом алгоритме для решения задачи. Аналогичным рассуждением о перемещении по вертикали, приходим к выводу, что число команд, касающихся перемещению по горизонтали должно быть нечетным в любом алгоритме для решения задачи. Значит, число команд в любом алгоритме для решения задачи будет четным! Теперь мы можем ответить на вопрос пункта в) – такого алгоритма не существует.

Задача 195. Задача подталкивает ребенка к анализу алгоритма – не простому его выполнению, а анализу состава команд.

Для ответа на вопрос задачи необходимо вспомнить, в каком случае число закрашенных клеток не равно числу команд закрасить в алгоритме: в случае, если Робот стоит на уже закрашенной клетке, то в результате выполнения этой команды, раскраска клетки не меняется. Таким образом, чтобы ответить на вопрос задачи, надо в каждом алгоритме сосчитать число команд закрасить и вычесть из этого числа те команды, которые будут выполнены Роботом на уже закрашенной клетке.

Посмотрим внимательно на алгоритм А. Отбросим сначала все команды закрасить и проверим, не возвращается ли Робот в процессе выполнения алгоритма в те клетки, где уже побывал. Видим, что в алгоритме есть только команды вправо и вверх, поэтому Робот точно не сможет вернуться. Теперь проверим, нет ли в алгоритме команд закрасить, которые стоят подряд: в результате всех стоящих подряд команд закрасить будет закрашена ровно одна клетка. В конце алгоритма находим такую пару, значит, последнюю команду закрасить считать не надо. Считаем остальные команды закрасить и получаем ответ: в результате выполнения алгоритма А на поле будут 4 закрашенные клетки.

Аналогично исследуем алгоритм Б. Кроме команд закрасить в алгоритме есть только команды вправо, поэтому Робот не будет возвращаться в процессе выполнения алгоритма. В двух местах команды закрасить идут подряд – в результате выполнения всей серии будет закрашена одна клетка. Итак, в результате выполнения алгоритма Б на поле будут 3 закрашенные клетки.

Задача 196. Сильные дети, решившие задачу 194, решат эту задачу сразу, используя инварианты. Основной части детей предлагается поэкспериментировать и попытаться в процессе решения этой задачи подойти к этом выводу: если Робот вернулся в ту же клетку, с которой начала, то количество команд вверх в алгоритме должно быть равным количеству команд вниз. А количество команд вправо – равным количеству команд влево.

Впрочем, нарисовав путь Робота на клетчатой бумаге, многие дети смогут просто догадаться, какой команды не хватает: команды вправо.

Задача 197. Если при решении задачи 196 ребенок не пришел к обобщаемому выводу об инвариантах в программе, то для решения этой и следующей задачи ему придется их сделать. Если Коля стер одну из команд вверх, вниз, вправо или влево, Робот никак не сможет вернуться снова в ту же клетку – изменится баланс этих команд и Робот не дойдет на одну клетку до той клетки, из которой она начал выполнять алгоритм. Поэтому единственная возможность здесь – команда закрасить.

Задача 198. После того, как дети решили задачи 195 – 197, сделать вывод об инвариантах, необходимый для решения этой задачи, им будет уже несложно. Тем более, что задача сформулирована очень понятно, на «бытовом», понятном ребенку уровне и поле Робота задано и ограничено. Так что ничего не должно испугать и помешать каждому ученику сделать правильный вывод. Другое дело, что сформулировать этот вывод слабым детям может быть трудно. Помогите им в этом – обсудите с ними решение индивидуально, и в процессе обсуждения помогите правильно сформулировать их объяснения и выводы.

Задача 199. В данном случае, все элементы последовательности должны выбираться из множества У, при этом не обязательно, что эти элементы должны встречаться в последовательности ровно 1 раз – в последовательности могут быть и одинаковые. Можно построить ровно 4 последовательности, соответствующие условию задачи.

Ответ:

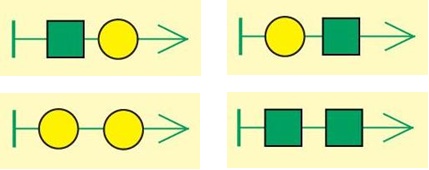
Задача 200. Необязательная. Классическая задача на «обход» точек (здесь: клеток). Это только кажется, что решить ее совсем легко – на самом закрашенные клетки стоят так «неудобно», что придется потрудиться, подыскивая способы обхода. Как всегда, надо дать возможность ребенку попробовать решить ее самостоятельно. Для этого хорошо бы иметь под рукой несколько запасных копий этого раскрашенного поля. Если вы видите, что ребенок потратил относительно много времени, но так и не смог продвинуться в решении, дайте ему новый «толчок» в решении: покажите, что обходить клетки можно не только по вертикали (до конца вверх, потом до конца вниз и т. д.) или по горизонтали (до конца вправо, до конца влево и т. д.). Можно обходить и по диагонали, лесенкой. Именно этот метод обхода клеток и помогает здесь найти решение.

Ответ:

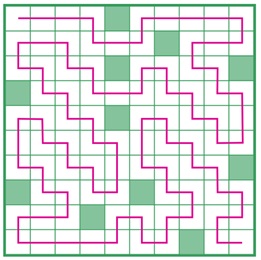
Задача 201. Подсказкой в данной задаче на разрезание являются две треугольные части. Наиболее естественная догадка о том, что они, скорее всего, должны принадлежать разным частям, оказывается верной. Теперь остается к каждому треугольнику добавить по 2 клетки так, чтобы части оказались действительно равными.

Ответ:

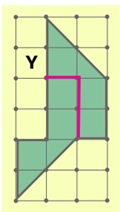
Задача 202. В настоящий момент эта задача не должна вызвать у ребят проблем. Если кто-то из ребят не может сдвинуться с места, он, скорее всего, забыл, что такое объединение и пересечение множеств. Вспомните вместе с ним или просто попросите найти соответствующий лист определений.

В пункте а) мы ищем пересечение, значит, нам нужны бусины, которые есть в обоих описанных множествах – одновременно и красные, и треугольные. Такая бусина у нас одна и искомое множество – множество В. Возможно, кого-то поставит в тупик задание пунктов в) или г). Эти пункты можно обсудить всем классом и закончить обсуждение выводами. Первый вывод – пересечение двух множеств, одно из которых равно подмножеству другого равно множеству-подмножеству. Второй вывод – объединение пустого множества с непустым множеством равно этому непустому множеству.

Ответ: