Компьютерное дополнение к курсу Информатика 5. 2024

Уроки 26–27. «Исполнитель Кузнечик. Состояние исполнителя»

Исполнитель Кузнечик, как и исполнитель Водолей – это семейство исполнителей. У каждого исполнителя из этого семейства своя система из двух команд: одна из них переводит Кузнечика на несколько шагов вперед, а другая – на несколько шагов назад. Возможности Кузнечика зависят от соотношения числа шагов при команде «вперед» и числа шагов при команде «назад». Если эти два числа взаимно простые (наибольший общий делитель их равен 1), то Кузнечик может добраться для точки 1 (может сдвинуться на 1 шаг), а, значит, сможет добраться и до любой точки числовой прямой. Если два числа при командах Кузнечика не взаимно просты (их наибольший общий делитель больше 1), то Кузнечик может попасть только в те точки числовой прямой, числа при которых кратны этом наибольшему общему делителю, а в другие точки попасть не сможет. Этот факт дети выведут для себя постепенно, решая задачи ученика и компьютерного практикума. Таким образом, исполнитель Кузнечик служит хорошим подспорьем при освоении темы «Делимость чисел».

Состояние исполнителя

Состояние исполнителя – еще одно важное понятие, связанное с исполнителями, которое должны усвоить школьники. Ниже перечислено основное, что нужно знать про состояния. При перечислении мы использовали «взрослую» терминологию, так как это книга для учителя. В учебнике использован более понятный школьнику язык, поэтому с учениками стоит говорить простым языком учебника.

1.         Состояние исполнителя полностью определяет поведение исполнителя при выполнении любой команды. Например, для исполнителя Водолей, чтобы знать, как он будет себя вести при выполнении команд, необходимо и достаточно знать текущее количество воды в каждом стакане. Напомним, что вместимость сосудов мы считаем частью описания исполнителя, так как Водолей – это на самом деле семейство исполнителей, каждый вариант исполнителя Водолей задаётся набором чисел – вместимостью трёх сосудов. Поэтому вместимость мы не включаем в описание состояния, подробнее об этом мы поговорим при обсуждении понятия обстановка в следующих уроках.  Нет необходимости включать в понятие состояния исполнителя Водолей и сведения о том, сколько воды было в каждом стакане до начала переливаний, потому что эти сведения не нужны для определения поведения Водолея при выполнении команд из текущего состояния   С другой стороны, знать количество воды только в двух стаканах из трех недостаточно для «предсказания» поведения Водолея. Поэтому количество воды только, скажем, в стаканах A и B не является полным описанием состояния этого исполнителя.

Итак, в понятие состояния исполнителя мы включаем только те условия ил данные которые необходимы для полного определения его поведения при выполнении любой из возможных команд.

2.         Мы рассматриваем в курсе только формальные исполнители. Это означает, что состояние такого исполнителя описывается определенным формальным объектом, вид этого объекта (число, слово, расположение фишек на игровом поле и пр.) – свой для каждого исполнителя. Например, для исполнителя Водолей состояние исполнителя можно представить тройкой неотрицательных целых чисел: <X_A,  X_B,  X_C>, где X_A, X_B и X_C – количество мер воды, которое в данный момент находится соответственно в сосуде A, B и С.

3.         Для каждого формального исполнителя определено множество допустимых состояний. Например, для Водолея – это множество допустимых троек вида <X_A,  X_B,  X_C>, где X_A X_B,  X_C – целые числа, причем

0 ≤  X_A  ≤ V_A

0 ≤  X_B  ≤ V_B

0 ≤  X_C  ≤ V_C

где V_A,  V_B,  V_C – соответственно объемы сосудов A, B и С.

4.         С каждой командой-приказом связана функция (правило), которая переводит каждое состояние исполнителя в новое состояние. Действие, выполняемое исполнителем, и состоит в преобразовании исходного состояния в новое состояние в соответствии с этой функцией. Как правило, эти функции несложно описать формально. В качестве упражнения попробуйте формально описать функцию, соответствующую команде «вылей из A» исполнителя Водолей. Пятиклассников этим формализмом загружать, конечно, не стоит.

5.         Аналогично, с каждой командой-вопросом связана функция, которая переводит исходное состояние исполнителя в одно из логических значений из множества {ИСТИНА, ЛОЖЬ}.

6.         Некоторые команды исполнителя для некоторых его состояний могут быть невыполнимы – такая ситуация называется отказ. На языке функций это означает, что соответствующая функция не является всюду определенной. Пример такой ситуации: команда «перевези козу» в исполнителе Перевозчик невыполнима, если коза и лодка находятся на разных берегах реки. Другие примеры отказов встретятся нам при обсуждении исполнителя Робот.

Задача 166. Простая задача на понимание материала листа определений.

Ответ:

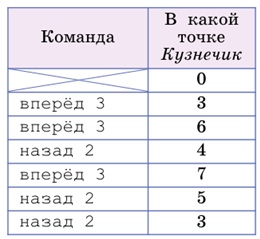
Задача 167. Состояние Водолея (при заданной вместимости сосудов) описывается тем, сколько мер воды в данный момент налито в каждый сосуд, значит, для Водолея с тремя сосудами есть три характеристики состояния: количество воды в А, количество воды в В, количество воды в С. Количество воды в А скорее всего изменится, если дать команду наполни А. Количество воды в В скорее всего изменится, если дать команду наполни B. Количество воды в С скорее всего изменится, если дать команду наполни C.

Состояние Кузнечика определяется точкой на числовой прямой, где он находится. Состояние Кузнечика изменится, если, например, дать команду вперед 3. При выполнении этой команды из начального состояния Кузнечик перейдет в точку 3.

Задача 168. Компьютерный практикум (см. комментарий к задаче 142). Вы можете составить задачи сами или воспользоваться задачами, данными в конце учебника.

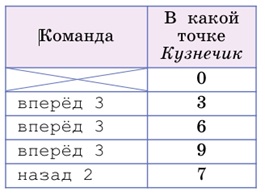
Задача 169. Запишем данные из задачи в таблицу:

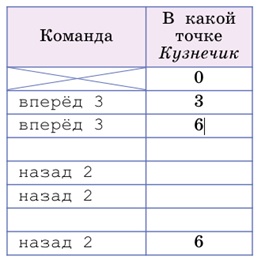
Видим, что после выполнения двух первых команд программы Ч Кузнечик окажется в точке 6. И после выполнения всей программы он должен оказаться в точке 6.

Конечно, можно пытаться достраивать программу Ч методом проб и ошибок. Но тут явно «напрашиваются» рассуждения. Посмотрим на таблицу внимательно: Кузнечик из точки 6 должен попасть обратно в ту же точку 6, выполнив при этом три команды назад 2 (которые перемещают его на 6 шагов назад) и еще две неизвестные команды. Следовательно, неизвестные команды должны перевести Кузнечика вперед на 6 шагов. Значит, это две команды вперед 3.

Как обычно, не стоит форсировать события и пытаться объяснить, какими рассуждениями можно решить эту задачу перед тем, как ребята начнут ее решать. Но если есть возможность, после того, как большинство ребят задачу решит, можно провести общее обсуждение, спросить, кто как решал и кто как рассуждал.

Ответ:

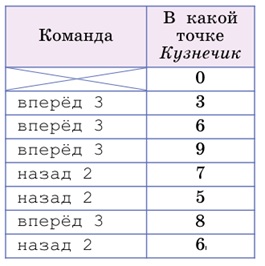
Задача 170. Качественная задача об исполнителе Кузнечик. Детям, которые затрудняются в решении, предложите для начала поэкспериментировать: написать такую программу, о которой идет речь в задаче, и посмотреть, куда попадет Кузнечик в результате ее выполнения. Можно написать и какой-нибудь другой вариант программы и также проверить, куда попадет Кузнечик. И, накопив такой экспериментальный опыт, можно сделать выводы.

Ответ: Кузнечик окажется в точке 4.

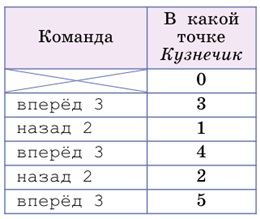
Задача 171. Задача, условие которой выглядит не простым, на самом деле оказывается несложной. Последовательность команд в программе практически полностью определяется условием о том, что, выполняя программу, Кузнечик не должен выходить за пределы отрезка от 0 до 5.

Действительно, из начального состояния в точке 0 Кузнечик может выполнить только команду – вперед 3, иначе он выйдет за пределы указанного отрезка. Из точки 3, в которой Кузнечик теперь окажется, он сможет выполнить только команду назад 2, потому что иначе опять-таки выйдет за границы отрезка. Из точки 1, в которой теперь окажется Кузнечик, он сможет выполнить только команду вперед 3 и оказаться в точке 4. Из точки 4 он сможет выполнить только  команду назад 2 и оказаться в точке 2. Из точки 2 он сможет пойти и вперед, и назад, но на этом этапе уже ясно, что надо идти вперед, чтобы попасть в точку 5 и таким образом выполнить все условия задачи.

Ответ:

Задача 172. Необязательная. Теперь в задачах о площади многоугольника на сетки дети сами могут выбрать способ решения – разрезать на части или достраивать до прямоугольника. В данной задаче годятся оба способа.

Ответ: площадь многоугольника Я равна 9 ед. кв.

Задача 173. Необязательная. Задача среднего уровня сложности. Все утверждения в задаче касаются натуральных чисел. Для правильного определения истинности надо хорошо уметь оперировать с терминами: двузначное, трехзначное, четное, нечетное, делится, не делится и пр. Если вы видите, что кто-то из учащихся допустил в этом задании ошибку, выясните, правильно ли он понял утверждение. При обсуждении утверждений А и В достаточно просто спросить, о каком числе идет речь, а при обсуждении утверждений C и D – поговорить о том, как ребенок считал числа.

Ответ: утверждение В – ложно, все остальные утверждения истинны.

Задача 174. Конечно, эта задачка для пятиклассников совсем простая. Но интересна именно тем, что обычная текстовая математическая задача, оказывается, может быть решена с помощью Кузнечика!

Будем использовать Кузнечика с системой команд вперед 3 и назад 2. Тогда выполнение команды вперед 3 будет соответствовать тому, что Костя даст Диме 3-рублевую монету, а выполнение команды назад 2 будет соответствовать тому, что Дима даст Косте 2-рублевую монету. Нужно написать такую программу для Кузнечика, чтобы в результате ее выполнения Кузнечик оказался в точке 7 – чтобы всего Костя дал Диме 7 рублей.

Написать такую программу несложно, вот она:

Осталось «проинтерпретировать» эту программу в условиях задачи.

Ответ: Костя должен дать Диме три 3-рублевых монеты, а Дима должен дать ему сдачи одну 2-рублевую монету.

Задача 175. Качественная задача об исполнителе Водолей. Задача непростая, потому что касается не какого-то одного варианта исполнителя Водолей с заданной вместимостью сосудов, а Водолея с любой вместимостью трех сосудов и при этом рассматриваемое состояние Водолея (то, сколько воды уже налито в каждый сосуд) тоже может быть любым! Такая слишком общая ситуация может поставить учащихся в тупик. Поэтому стоит начать с конкретных примеров. Поэкспериментировать можно на бумаге (теоретически), а можно и практически – на компьютере.

Выполнив достаточно много экспериментов, дети смогут убедиться, что общее количество воды в сосудах не меняется. Действительно, при выполнении команды перелей из … в … вода, которая уже есть в сосудах, не выливается и новая вода не добавляется. Таким образом, сколько бы команд такого вида перелей из … в … ни выполнял Водолей, общее количество воды в сосудах на столе не изменится. При этом как именно это количество воды будет распределено по сосудам – неизвестно и зависит от того, какие именно команды выполнил Водолей.

Итак, в этой задаче количество воды в сосудах не изменяется. Иногда ту же мысль выражают так: «общее количество воды в трех сосудах – это инвариант команды переливания». Понятие инварианта, то есть величины, которая не изменяется в ходе преобразований определенного вида, – понятие, важное не только для информатики, но и для науки вообще. Например, закон сохранения энергии означает, что количество энергии в замкнутой физической системе – инвариант относительно физических преобразований.  В нашем курсе понятие инварианта неявно будет возникать в задачах, но явно вводиться не будет.

Для команд «налей…» и «вылей…» общее количество воды в сосудах не является инвариантом, но может изменяться только монотонно (не убывает для команды «налей…» и не возрастает для команды «вылей…»), такие величины иногда называют полуинвариантами. Полуинварианты, как и инварианты, важны для анализа алгоритмов.

Если задача 175 оказалась слишком трудной, в качестве подготовительной можно использовать такую задачу:

Задача. Исполнителю Водолей дали команду «перелей из A в B». Среди трех приведенных ниже утверждений, укажи те, которые являются истинными. В тех случаях, когда ты считаешь утверждение истинным, приведи пример. В тех случаях, когда ты считаешь утверждение ложным, попробуй объяснить, почему ты так считаешь.

1)  Существуют такие объемы стаканов и такие объёмы воды в каждом из стаканов, что после выполнения команды общий объем воды в стаканах увеличился.

2)  Существуют такие объемы стаканов и такие объёмы воды в каждом из стаканов, что после выполнения команды общий объем воды в стаканах остался прежним.

3)  Существуют такие объемы стаканов и такие объёмы воды в каждом из стаканов, что после выполнения команды общий объем воды в стаканах уменьшился.

Решение. В первом и третьем случае ответ «нет», во втором случае ответ «да». При выполнении команды переливания вода только перераспределяется между сосудами. Она не доливается извне и не выливается «в никуда». Поэтому общее количество воды в сосудах не изменяется. По условию задачи ученикам нужно привести примеры, когда общее количество воды в трех стаканах не изменилось. Это происходит всегда! Однако в некоторых случаях не меняется и количество воды в каждом сосуде в отдельности (это выполняется, если вначале сосуд В был пуст или сосуд А был полон), а в других случаях количество воды  в отдельных сосудах меняется (во всех остальных случаях).

Полезно разобрать примеры разных типов: такие, в которых количество воды в стакане А не изменяется (стакан А пуст или стакан Б полон), и такие, в которых  количество воды в стакане А изменяется.

Задача 176. После того, как будет решена задача 175, эта задача не покажется детям слишком сложной. Действительно, общее количество воды во всех сосудах Водолея не меняется при выполнении команды вида перелей из … в …, поэтому и после выполнения программы Q, которая состоит только из таких команд, общее количество воды в сосудах Водолея не изменится. В начальном состоянии всего в сосудах было 3 × 3 = 9 мер воды, значит и после выполнения программы Q в трех сосудах вместе будет 9 мер. При этом в сосуде А 1 мера, в сосуде В – 5 мер, значит в сосуде С будет 3 меры воды.

Ответ: после выполнения программы Q в сосуде С будет 3 меры воды.

Задача 177. Необязательная. Задача на построение последовательности из бусин данного множества по описанию. В комментариях к задаче 65 мы подробно обсудили этот тип задач. Напомним, что второе утверждение – «Каждая бусина этой последовательности содержится в множестве Т» – означает, что бусины для построения последовательности мы можем выбирать только такие, которые есть в множестве Т. При этом в последовательности будут и одинаковые бусины, ведь длина последовательности 6, а в множестве всего 3 бусины.

Из условия задачи и первого утверждения следует, что в последовательности будет три желтых квадратных бусины (желтые, потому что мы можем брать квадратные бусины только те, которые есть в множестве Т). После каждой из этих квадратных бусин идет треугольная – синяя треугольная. Собственно, из этих трех пар и состоит цепочка – мы же набрали 6 бусин, больше нам и не нужно. Получаем, что задача имеет единственное решение.

Ответ:

Задача 178. Необязательная. Здесь ребенку предлагаются для работы древнееврейские буквы. Некоторые древнееврейские буквы используются в математике (обычно буква «алеф»).

Традиционное название этого алфавита (древнееврейский) не совсем точно. Возник он в древности, и именно им записан Ветхий Завет и другие классические иудейские религиозные тексты. В повседневной жизни бóльшая часть иудаистов уже многие сотни лет назад перешли на другие языки, но в качестве письменного языка продолжали использоваться древнееврейский. С XIX в. на еврейском языке стала возникать светская литература, поэтому в нем, естественно, появилось много новых слов для обозначения ранее не существовавших понятий, а также несколько изменилась грамматика. Сам обновленный язык называется теперь «иврит», это государственный язык Израиля, многие евреи в других странах стали его использовать не только в литературе, но и в быту. За последние столетия получили литературную обработку и другие языки евреев, наиболее известный из них – идиш, язык евреев Центральной и Восточной Европы, в основе его лежат немецкие диалекты. В некоторых регионах (в Крыму, Дагестане, Средней Азии и т. п.) евреи пользовались такими языками, как тюркский, иранский и др., но если эти языки использовались на письме, древний алфавит оставался неизменным.

В древнееврейской письменности каждая буква обозначает какой-то согласный звук плюс произвольный гласный. Направление письма – справа налево.

Мы приводим здесь древнееврейские буквы и их названия.

Хаотичным просматриванием здесь найти три одинаковые фигурки практически невозможно. Необходимо организовать полный перебор, по ходу вычеркивая просмотренные элементы, вместе с буквами, равными им. И даже после этого ответ находится не мгновенно, так что задача в любом случае займет некоторое время. Ответ здесь учащиеся могут написать одним из двух способов: либо попробовать изобразить в тетради одинаковые буквы, либо указать их место в строках. При дефиците времени можно предложить ее для домашней работы.

Ответ: одинаковые буквы – четвертая с конца в первой строке, седьмая во второй строке, последняя в третьей строке.