Компьютерное дополнение к курсу Информатика 5. 2024

Урок 25. «Исполнитель Удвоитель»

Несмотря на внешнюю простоту этого исполнителя, решение задач об Удвоителе очень полезно для знакомства детей со степенями двойки (заодно и пропедевтикой работы с двоичным счислением), с понятием эффективности программы, методом решения задачи «с конца».

Будем называть программу более эффективной, если она также решает поставленную задачу, но при этом содержит меньше команд. Написать какую-нибудь программу для решения задачи об Удвоителе не очень сложно. При попытке найти более эффективную программу задача становится сложнее. Поиск наиболее эффективной программы (содержащей наименьшее возможное количество команд) – уже очень неординарная задача, связанная с построением доказательства. Таким образом, решение одной и той же задачи для Удвоителя может быть как совсем несложным и доступным даже слабым ученикам, так и (при ограничении количества команд) трудной и даже проектной задачей: при решении такой задачи можно организовать соревнование между учащимися, общее обсуждение и анализ решений.

Конечно, мы не будем требовать от пятиклассников доказательства наибольшей эффективности написанной им программы – доказательства того, что меньше команд использовать невозможно. На первых порах достаточно того, что ученик задумается над этим, попытается построить как можно более эффективную программу, посмотрит на решения других учеников, примет участие в их проверке и обсуждении.

Построение максимально эффективной программы основывается на том очевидном факте, что команда умножь на 2 продвигает Удвоителя вперед быстрее, чем команда прибавь 1, уже начиная с числа 2. Поэтому чем больше команд умножь на 2  в программе, тем быстрее Удвоитель приближается к цели и тем меньшее количество команд получается в программе. При этом выгоднее оказывается удваивать как можно бóльшее число – чем бóльшее число удваивается, тем дальше продвигается Удвоитель. Все эти соображения будут понятны детям после того, как они решат нескольких первых задач об Удвоителе. Многие дети сами придут к этим выводам, слабых учащихся придется к этим выводам подтолкнуть.

Какие же выводы можно сделать из перечисленных нами наблюдений? Чтобы составить программу покороче, надо постараться использовать как можно больше команд умножь на 2, при этом, если есть выбор, лучше ставить эти команды ближе к концу программы, чтобы удваивались бóльшие числа. Раз так, давайте и строить программу с конца. Если целевое число четное, то оставим последней командой умножь на 2. Если целевое число нечетное, придется поставить в конце одну команду прибавь 1, а сразу перед ней уже умножь на 2. Идем дальше от конца программы к началу. Вычислим, какое число получится на экране удвоителя перед последней (парой последних) написанной нами командой. Для этого делим целевое число пополам (или сначала вычитаем их него 1, а потом делим пополам). Тогда таблица будет выглядеть, например, так:

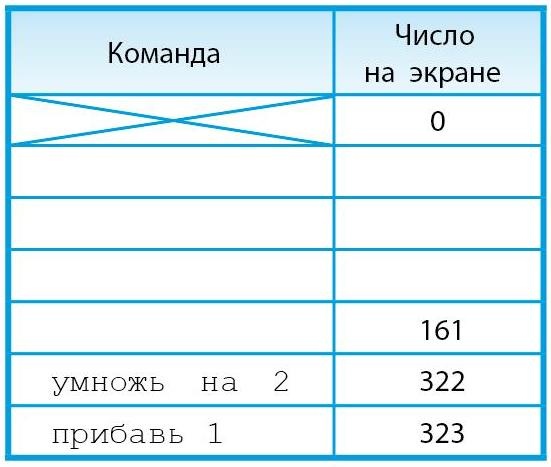
Продолжаем строить программу, идя от конца к началу. Напротив полученного числа (в нашем примере это 161) нам бы тоже хотелось оставить команду умножь на 2: ставим ее, если число четное. Если число нечетное, что ставим сначала команду прибавь 1, а перед ней – умножь на 2.

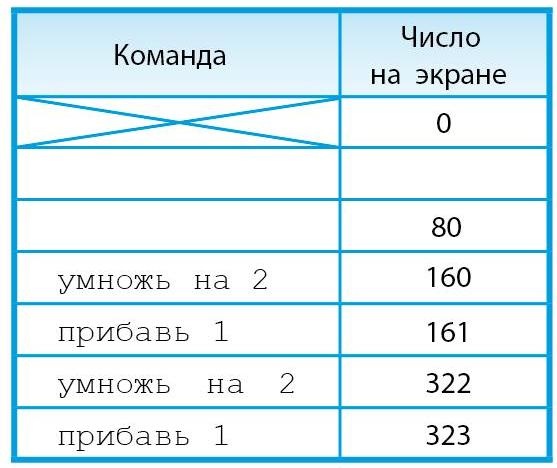
Так строим программу от конца к началу, пока число в правой колонке не станет равным 0. Каждый раз текущее число в таблице будет либо четным, либо нечетным, другого варианта быть на может. Напротив четного числа мы ставим команду умножь на 2. Напротив нечетного числа ставим команду прибавь 1, а перед ней – умножь на 2. Таким образом мы ставим в программу максимально возможное число команд умножь на 2, при этом стоят они максимально близко к концу программы. Значит, пользуясь таким способом, мы построим наиболее эффективную программу для Удвоителя – программу с наименьшим количеством команд.

Детям прийти к такому способу построения эффективной программы позволит опыт, накопленный ими при решении задач. Поэтому не стоит требовать от детей построения эффективной программы сразу с первых задач. 

Задача 157. Простая задача на понимание материала листа определений.

Ответ:

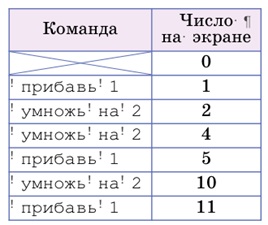
Задача 158. Чтобы восстановить данную программу, сделаем сначала заготовку таблицы, куда занесем все, что дано в задаче:

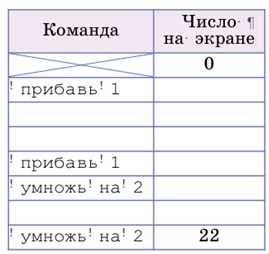
Пока задача не выглядит простой. Применим наш излюбленный метод проб и ошибок. Поставим на всех пропущенных местах команду умножь на 2:

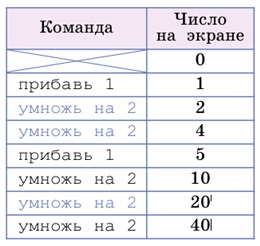
Результат получился большим, чем нужно. Попробуем заменить одну из написанных нами команд на прибавь 1:  если заменить команду, стоящую на втором месте в программе, результат не изменится:

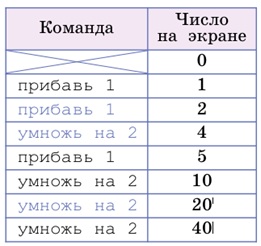
Если заменить ту команду, которая стоит на третьем месте: результат изменится, но не будет правильным:

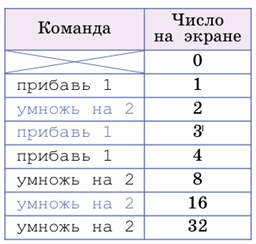
А если заменить ту команду, которая стоит на предпоследнем месте –результат получится тот, который нам нужен:

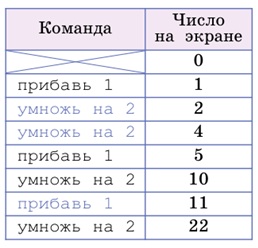
Если быть наблюдательным, можно увидеть, что программа Ф только на одну команду длиннее программы М из предыдущей задачи, это команда умножь на 2, и результат работы программы Ф вдвое больше результата программы М! Проверим, можно ли заполнить пропуски в программе Ф теми командами, которые есть в программе М – можно! Значит, программа Ф получается добавлением к программе М одной команды умножь на 2.

Ответ:

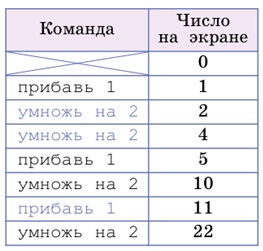
Можно решать эту задачу и по-другому: рассматривая программу с конца. Итак, вот данные из условия задачи:

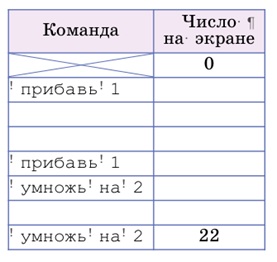
Последняя команда умножь на 2, поэтому предыдущее число в таблице – 11:

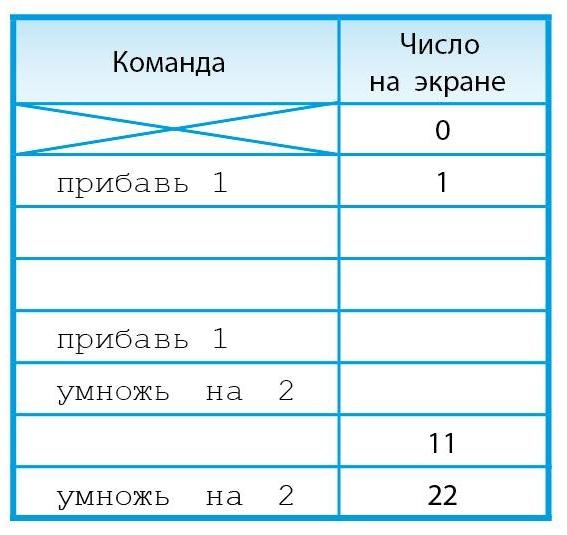
Число 11 нечетное, оно не может быть получено в результате команды умножь на 2, значит, предпоследняя команда должна быть прибавь 1. Ставим эту команду в таблицу, заполняем колонку числами, насколько теперь это стало возможным:

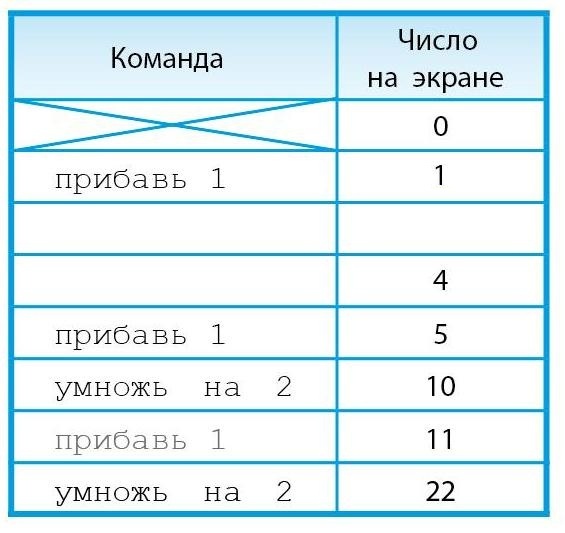
Осталось заполнить две строки – найти две команды, с помощью которых можно из числа 1 получить число 4. Из 1 любая из двух возможных команд дает 2. Чтобы из 2 получить 4, надо умножить на 2. Таким образом, первая из искомых двух команд может быть любой, а вторая команда должна быть умножь на 2. Задача решена.

Задача 159. Для начала составим одну программу, выполнение которой дает результат 15. Можно было бы действовать методом проб и ошибок, но так как никаких ограничений на длину программы в задаче нет, можно порассуждать, как удвоением и добавлением единиц поучить из 0 число 15. Понятно, что сначала надо добавить 1 – удваивать нуль бессмысленно. Теперь можно удваивать – так число быстрее увеличивается. После трех удвоений получится число 8 – дальше удваивать нельзя, потому что получится число, большее 15, а уменьшать число Удвоитель не умеет. Значит, после получения числа 8, надо добавить нужное число единиц. Получили такую программу (будем записывать ее в таблицу, чтобы все время контролировать результат):

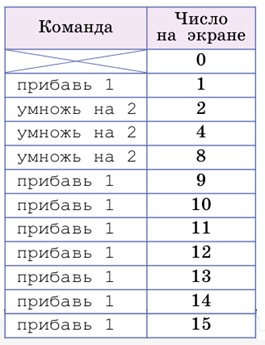
Теперь нужно составить другую программу с тем же результатом. Можно просто 15 раз добавить по 1, но этот вариант мы оставим про запас как очевидный. Можно поискать и другие варианты.

Если будет возможность, обсудите с детьми, какая пара решений у кого получилась, у кого программа получилась самой короткой, у кого – самой длинной. Сильным детям можно предложить попробовать составить программу длиннее 15 команд (программа в 15 команд – это 15 раз  прибавь 1), можно в начало добавить сколько угодно команд умножь на 2 и получится программа любой бóльшей длины) и короче 7 команд (это не получится).

Задача 160. На первый вопрос можно ответить просто: нажать 99 раз на кнопку прибавь 1. Но выписывать такую программу будет скучно, поэтому лучше сэкономить силы и добавить в программу несколько команд удвоения.

Для ответа на второй вопрос программу надо оптимизировать – сделать существенно короче. Для этого постараемся как можно больше использовать команду умножь на 2 – эта команда позволяет «наращивать» результат гораздо быстрее (за меньшее число команд), чем прибавь 1.

Будем удваивать сразу, начиная с 1 – у нас будут получаться числа 1, 2, 4, 8, 16, 32, 64. Дальше придется прибавлять 35 раз по 1 и мы точно не уложимся в 10 команд.

Попробуем удваивать, начиная с тройки: 1, 2, 3, 6, 12, 24, 48, 96, 97, 98, 99. Мы использовали 11 команд – почти уложились:

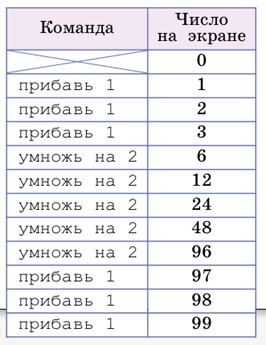
Посмотрим, нельзя ли улучшить эту программу,  чтобы поменьше единиц добавлять в конце. Хорошо бы удвоением получить сразу число 98, чтобы в конце добавить 1 только один раз. Для этого надо удвоить число 49. У нас в промежуточных результатах есть число 48 – попробуем исправить программу после этого числа:

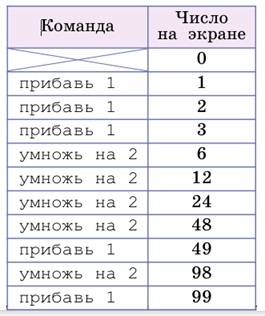
Мы уложились ровно в 10 команд и получили ответ на второй вопрос задачи.

Как видите, решение «в лоб» получилось довольно объемным. Мы надеемся, что некоторые из ваших учеников, попытавшись решить ее прямым путем, интуитивно придут к способу решения «с конца»: если применить описанный нами способ построения эффективной программы, получится программа из 9 команд. Поддержите ребят, которым придет в голову начать с конца, помогите им довести свой способ решения до конца. Но, конечно, ожидать такой способ решения от большинства детей, еще рано.

Задача 161. После того, как дети решили две предыдущие задачи, эта задача будет совсем нетрудной, не смотря на то, что для ее решения не предполагается выписывание полной программы, а требуются рассуждения. После первого нажатия кнопки прибавь 1 получится число 1, после второго – 2 и так далее. Значит, число 13 получится после 13-го нажатия.

Задача 162. Необязательная. Продолжаем работать с исполнителем Водолей. Задачи такого типа мы называем «качественными»: для их решения не надо строить программу, а надо рассуждать, рассматривать все возможности, иногда строить доказательство.

Ответ на вопрос пункта а) может быть очевидным: 1 мера. Для ответа на вопрос пункта б) придется рассуждать и перебирать варианты и доказывать полноту ответа. Для пятиклассников это не просто, поэтому задача помечена как необязательная.

Для начала будем перебирать варианты: 1 мера, очевидно, годится.

Пусть вместимость сосуда В – 2 меры. Тогда мы можем налить полный сосуд А и перелить из него в сосуд В 2 меры – в А останется 1 мера. Значит, и этот вариант годится.

Пусть вместимость сосуда В – 3 меры. У нас получатся два одинаковых сосуда, как бы мы их не наливали полными, не переливали друг в друга – они будут всегда оставаться либо пустыми, либо полными, т. е. с помощью этих сосудов мы можем получить только 3 меры. Значит, этот вариант не годится.

Пусть вместимость сосуда В – 4 меры. Наливаем полный сосуд В, переливаем из него в А и в В остается 1 мера. Этот вариант годится.

Пусть вместимость сосуда В – 5 л. Наливаем полный А и переливаем его в В два раза – в А останется 1 мера. Этот вариант годится.

И так далее, просмотрев несколько вариантов, попробуем обобщить результаты. Можно выделить три группы результатов:

1)         Число мер в сосуде B кратно 3 (3, 6, 9, 12….). Это можно записать так: V_B = 3x; здесь V_B – объем сосуда B, x – произвольное натуральное число (1, 2, 3, …).

2)         Число мер в сосуде B при делении на 3 дает остаток 1 (1, 4, 7, 10, ...).  Это можно записать так: V_B = 3x + 1; здесь V_B – объем сосуда B, x –произвольное натуральное число или 0.

3)         Число мер в сосуде B при делении на 3 дает остаток 2 (2, 5, 8, 11, ...).  Это можно записать так: V_B = 3x +2; здесь V_B – объем сосуда B, x –произвольное натуральное число или 0.

При делении на 3 могут быть только 3 остатка: 0 (в случае, если число делится на 3), 1 и 2. Значит, мы рассмотрели все возможные варианты.

Рассмотрим каждый случай отдельно.

1.         Число мер в сосуде B кратно 3.  В этом случае мы можем получать только количества, кратные 3. Поэтому 1 меру получить нельзя. 

2.         Число мер в сосуде B при делении на 3 дает остаток 1, т. е. V_B = 3x + 1. Получить 1 меру можно. Для этого достаточно налить полный сосуд В (тем самым налить в него 3x + 1 мер). А затем отливать из него по 3 литра, используя сосуд A.  После x переливаний мы выльем 3x мер, а в сосуде B останется 1 мера.

3.         Число мер в сосуде B при делении на 3 дает остаток 2, т. е. V_B = 3x + 2. И в этом случае можно получить 1 меру, но действовать будем иначе. Будем наливать воду полный сосуд A, а затем переливать эти 3 меры в сосуд B. После x таких переливаний в сосуде B будет 3x мер и останется свободным объем в 2 меры. Нальем последний  раз 3 меры в сосуд A и перельем из A в B. В сосуде А при этом останется 3 – 2 = 1 мера.

Как видите, задача такая объемная, а решение ее получается настолько общим, что эта задача вместе с продолжающей ее задачей 163 вполне могут стать предметом для обсуждения на проектном уроке. На таком уроке, проведя предварительное обсуждение, можно разделить класс на 3 группы и попросить каждую группу исследовать один из перечисленных вариантов.

Задача 163. Необязательная. Еще одна качественная задача, являющаяся прямым продолжением задачи 162.

По опыту, полученному при решении задачи 162, рассмотрим 6 вариантов в зависимости от остатка при делении на 6.

Если вместимость сосуда В будет кратна 6, то и налить мы сможем только объем, кратный 6 мерам.

Если вместимость сосуда В равна 6х + 1. Тогда перельем из В а А х раз и после этого в В останется 1 мера. Вариант годится.

Если вместимость сосуда В равна 6х + 2. Это число четное – оно точно делится на 2: (6х + 2) : 2 = 3х + 1. Тогда у нас есть два сосуда, вместимость каждого четное число мер. С помощью этих сосудов мы сможем получить только четное число мер, значит 1 меру получить не сможем. Этот вариант не годится.

Если вместимость сосуда В равна 6х + 3. Это число кратно 3: (6х + 2) : 3 = 2х + 1. Тогда у нас есть два сосуда, вместимость каждого число мер, которое кратно 3. С помощью этих сосудов мы сможем получить только число мер, красное 3. Значит 1 меру получить не сможем. Этот вариант не годится.

Вариант 6х + 4 тоже не годится, потому что это число четное.

Если вместимость сосуда В равна 6х + 5. Тогда перельем из А а В х + 1 раз и после этого в А останется 1 мера. Вариант годится.

Ответ: чтобы можно быть получить 1 меру, вместимость сосуда В должна быть таким числом, которое при делении на 6 дает либо остаток 1, либо остаток 5.

Задача 164. Площадь такого треугольника можно найти только достроив его до прямоугольника и вычтя из площади этого прямоугольника площади трех прямоугольных треугольников:

15 – 4½ – 2 – 2½ = 6 (ед. кв.)

Ответ: площадь треугольника К равна 6 ед. кв.

Задача 165. Аналогичные задачи ребятам уже встречались. Как обычно мы предлагаем решать подобные задачи, строя схему с множествами.

Для начала построим привычную схему с пересечением двух множеств: множества К детей, которые были в краеведческом музее и множества Х детей, которые побывали в художественном музее. По условию задачи  в множестве К – 20 элементов, в множестве Х – 17 элементов, в пересечении этих множеств 9 элементов:

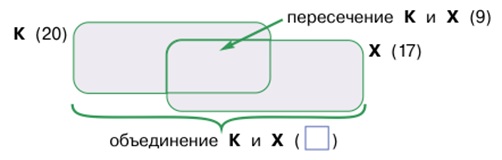
Теперь, пользуясь этой схемой, мы можем вычислить, сколько элементов множества К лежит вне пересечения с множеством Х: 20 – 9 = 11. Аналогично вычисляем, сколько элементов множества Х лежит вне пересечения с множеством К: 17 – 9 = 8. Отметим это на схеме:

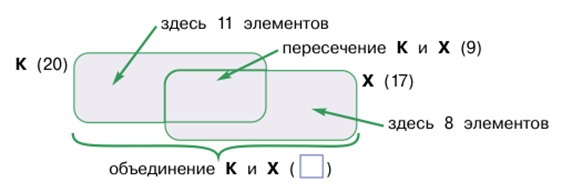
Мы на схеме добавляем только стрелки с надписями, которые указывают, сколько элементов в указанной части множества. Но ребенок для наглядности может нарисовать и сами элементы множеств – например, можно нарисовать просто кружки. При этом кружки могут быть и одинаковыми, потому что мы помним, что в задаче за ними стоят разные ученики!

Теперь найдем, сколько элементов в объединении множеств Х и К:

11 + 9 + 8 = 28.

Итак, в экскурсиях (одной или двух) участвовало 28 человек. А всего в классе 30 человек. Значит, двое не были ни на одной экскурсии.

Ответ: двое учащихся не были ни в краеведческом, ни в художественном музее.