Страницы сайта
Текущий курс
Участники
Общее
Тема 1
Тема 2
Тема 3
Тема 4
Тема 5
Тема 6
Тема 7
Тема 8
Тема 9
Тема 10
Тема 11
Тема 12
Тема 13
Тема 14
Тема 15
Тема 16
Тема 17
Тема 18
Тема 19
Тема 20
Тема 21
Тема 22
Тема 23
Тема 24
Тема 25
Методический комментарий для учителя к уроку «Пересечение и объединение множеств»
Уроки 18–19. «Пересечение и объединение множеств»
Действия над множествами – новый вопрос, которого не было у нас в курсе начальной школы. Каковы же причины появления этой темы, традиционно изучавшейся в курсе математики?
Несколько слов о наших общих подходах
Мы хотели бы дать ребятам в курсе поменьше информации для запоминания и побольше общих подходов (идей, схем, методов) и материала для размышления. Информационные объекты, структуры и процессы в разных областях науки и жизни часто бывают организованы сходным образом. Поэтому можно их рассмотреть на понятных детям моделях и достичь понимания внутренней структуры. Впоследствии такие модели можно наполнить любым содержанием – это позволит учащемуся ускорить и качественно улучшить освоение нового материала. Именно такие конструкты впоследствии позволят ребятам анализировать, структурировать, обрабатывать информацию вне зависимости от ее содержания, а не рассматривать каждый информационный объект как совершенно новый.
Знакомство с действиями пересечения и объединения на примере наглядно представленных множеств бусин делает вопрос доступным и простым для понимания. При таком способе все описываемые действия можно провести непосредственно. Формируемая логическая схема обладает общенаучной ценностью и находит ряд важных применений. Кроме очевидного применения в области операций над множествами, дети получают возможность начального понимания утверждений с составными условиями с союзами «и», «или», что является пропедевтикой понимания составных условий в программах для исполнителей в курсе 6 класса.
Наша цель – не столько решение конкретных задач с операциями над множествами, сколько формирование содержательного понимания логики изучаемых операций. Поэтому у нас каждую задачу ребенок решает явно, работая с конкретными графическими объектами – как учебные задачи с множествами, так и традиционные арифметические задачи о множествах. В каждой такой задаче схема с множествами играет роль не просто визуальной опоры, но полной графической модели, по которой собственно ребенок и решает задачу – рисует, сопоставляет с условием, считает и т. п. В процессе этой деятельности у ребят постепенно формируются представления о количественных соотношениях между множествами, которые впоследствии позволяют им решать подобные задачи быстрее – так, как это принято в традиционных курсах математики.
По той же причине мы не вводим сразу знаки объединения и пересечения множеств: нам важно, чтобы дети разобрались с существом этих операций, а со знаковой записью они могут познакомиться и позднее – когда это потребуется в курсе математики.
Задача 92. Здесь требуется только понимание материала листа определений. Можно использовать пометки, как это было сделано на листе определений, только для каждой пары множеств они должны быть свои. Действительно, удобно помечать, например, галочками, все общие элементы множеств. Такие пометки оказываются полезными не только при построении пересечения, но и при построении объединения – это поможет не выписать общие элементы дважды.
Если попытаться формализовать проведение операций над множествами (это вам может пригодиться при работе со слабыми ребятишками), то это будет выглядеть так.
Построение пересечения множеств
- Берем из первого множества любой элемент. Проверяем, есть ли выбранный элемент в другом множестве. Если есть, то помечаем его галочкой в обоих множествах, если нет – переходим к следующему элементу первого множества.
- Так мы делаем до тех пор, пока в первом множестве не закончатся элементы.
- Рисуем множество-пересечение, в которое помещаем все элементы любого из двух множеств, помеченные галочкой.
Построение объединения множеств
- Берем из первого множества любой элемент. Проверяем, есть ли выбранный элемент в другом множестве. Если есть, то помечаем его галочкой в обоих множествах, если нет – переходим к следующему элементу первого множества.
- Так мы делаем до тех пор, пока в первом множестве не закончатся элементы.
- Рисуем множество-объединение, в которое помещаем все элементы одного из множеств и еще все элементы другого множества, которые не помечены галочкой.
Ответ:
а)
б)
в)

г)

д)

Задача 93. В этой задаче требуется содержательное понимание материала листа определения. Лишь одно из множеств задано в задаче явно, остальные представлены только словесным описанием. При этом мы не планируем, что дети будут сначала строить эти недостающие множества, а затем уже выполнять требуемые операции. Здесь требуется другое – содержательное понимание определений операций пересечения и объединения. В этом случае задача становится несложной.
Например, в пункте а) рассуждения могут быть такими. Нам нужно найти пересечение двух множеств, значит, нам нужны элементы, которые входят в каждое из этих множеств: в множество всех двузначных четных чисел и в множество Ю. Значит, искомое множество состоит из всех двузначных четных чисел, которые есть в множестве Ю.
Советуем вам продумать процесс проверки решения этой задачи заранее. Чтобы проверить решение у каждого учащегося, проходя по классу (как мы обычно советуем), придется потратить слишком много времени, поскольку чисел в множествах довольно много и ребята будут выписывать их в произвольном порядке. Можно организовать фронтальную проверку. При этом необходимо договориться, что один ученик медленно читает числа в множестве-ответе, а все остальные ребята помечают галочкой каждое услышанное число, которое есть и у него в ответе. Если ребята услышали какое-то число, которого у них нет, то они выписывают его отдельно внизу под ответом. При такой проверке все расхождения в ответах будут хорошо видны, и их уже можно обсуждать индивидуально. По такому же принципу можно организовать и парную проверку.
Ответ:
а)

б)

в)

г)

Задача 94. Здесь ребята впервые встречаются с ситуацией, когда нужно найти пересечение двух множеств, одно из которых равно подмножеству другого. В ходе решения этой задачи ребята поймут, что в таком случае пересечение совпадает с меньшим из множеств, подмножеством. Как и в предыдущей задаче, здесь совершенно необязательно явно выписывать каждое множество, а можно рассуждать, опираясь на определение пересечения множеств. Нам нужны все буквы, которые есть в русском алфавите и одновременно являются русскими согласными. Но русские согласные сами являются буквами русского алфавита, значит, искомое пересечение совпадает с множеством всех русских согласных.
Задача 95. Это сюжетная арифметическая задача, обычно решаемая в курсе математики. Но в ее решении предполагается использование введенных в курсе понятий – множества, пересечение множеств, объединение множеств. Наш подход к решению таких задач несколько отличается от того, который традиционно принят в математике: на вопросы о количестве элементов в множествах дети отвечают с помощью непосредственного пересчета, а не оговоренных арифметических действий. Данный способ подробно описан нами в указании. В этой первой подобной задаче мы предлагаем ребятам готовую схему с множествами, которую они должны лишь заполнить – найти на схеме все данные множества, написать все известные количества элементов.
Заготовку для схемы с множествами дети найдут на вкладыше тетради проектов.
Рассуждения здесь могут быть такими. Пересечение множеств желтых футболок и футболок с надписью содержит 3 элемента, нарисуем их – три кружка с буквами (буквы лучше использовать латинские, чтобы они не путались с заданными именами множеств). Всего в множестве желтых футболок 8 элементов, при этом 3 мы уже нарисовали в пересечении, значит на оставшемся от пересечения месте нарисуем 5 футболок (это желтые футболки без надписи). Всего у Саши 13 футболок (это объединение множеств). Значит, дорисуем на оставшемся от пересечения месте множества Н столько футболок, чтобы на картинке было всего 13 элементов – 5 элементов. Осталось подсчитать все элементы множества Н и написать ответ на вопрос задачи.
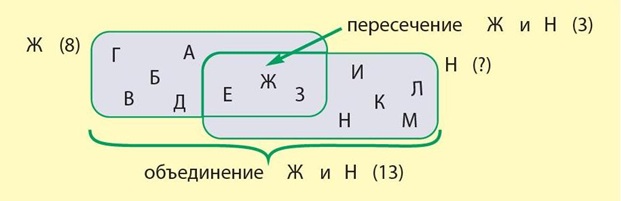
Ответ: у Саши 8 футболок с надписью.
Задача 96. Здесь можно с одинаковым успехом строить пересечения и объединения, как с помощью рисунков, так и с помощью рассуждений. Слабым ученикам в случае затруднения предложите нарисовать в тетради каждое из множеств, а затем уже выполнять указанную операцию. Рассуждения же могут быть, например, такими. В пункте а) нам нужны общие элементы множества треугольных бусин и множества красных бусин. Значит, нам нужны бусины одновременно красные и треугольные, такая бусина у нас одна. В пункте в) мы получаем в пересечении пустое множество, поскольку бусины у нас не могут быть одновременно круглыми и треугольными.
Ответ:
а)
б)
в)
Задача 97. Необязательная. Для решения этой задачи нужно понимание количественных закономерностей в операциях над множествами. Задачу проще всего решать методом проб и ошибок, в ходе которого это понимание постепенно сформируется. Можно сначала построить два любых множества чисел. В ходе первой же пробы большинству ребят станет ясно, что в каждом множестве должно быть не больше 8 чисел (иначе в объединении чисел будет больше 8) и не меньше 4 чисел (иначе в пересечении чисел будет меньше 4). Дальше можно проводить эксперименты более прицельно. Один из способов заключается в том, чтобы взять произвольное множество из 4 – 8 чисел, выбрать в нем 4 элемента, которые будут в пересечении множеств, и второе множество подстраивать к нему так, чтобы выполнялись условия задачи.
Для проверки ребят должны нарисовать схему с объединением и пересечением своих множеств.
Задача 98. Эта задача является обратной по отношению к задаче 96. Если кто-то из ребят затрудняется в ее решении или вообще не знает, что делать, можно предложить ему вернуться к задаче 96 и еще раз прочитать условие, просмотреть свое решение и уже потом снова браться за задачу 98. Ясно, что решение каждого пункта не единственно – подходящих пар множеств довольно много, но не все множества в них легко описать словами. Мы приводим здесь наиболее вероятные решения, но ребята, возможно, предложат вам другие.
Ответ: а) множество А равно пересечению множества всех красных бусин и множества всех круглых бусин;
б) множество Б равно пересечению множества всех зеленых бусин и множества всех треугольных бусин;
в) множество В равно объединению множества всех синих бусин и множества всех круглых бусин.
Задача 99. Эта задача решается по той же схеме, что и задача 95. Заготовку для схемы со множествами дети найдут на вкладыше тетради проектов. Если ребенок затрудняется, то предложите ему воспользоваться подробным указанием из задачи 95.
Размещаем 4 элемента в пересечении множеств Н и Ф. Теперь в оставшейся части множества Н размещаем элементы так, чтобы всего в Н было 12 элементов. Аналогично поступаем с множеством Ф.
Ответ: в составе группы приехало 22 туриста.
Задача 100. Для построения множества А используем первое и третье утверждения. При этом условие в третьем утверждении сразу дает пустое множество – итак, множества А пустое. Для построения множества В используем второе и четвертое утверждения: в множестве В нет круглых и квадратных бусин, значит в нем лежит только зеленая треугольная бусина.
Ответ:
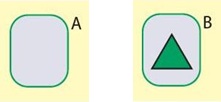
Задача 101. Подобные задачи нам уже встречались (задачи 93, 94, 96). Но это одна из немногих задач курса, в которой используются бесконечные множества (например, множество четных чисел). Такая ситуация полностью исключает возможность явного выписывания всех элементов множества, именно на такой задаче можно проверить, способны ли ребята выполнить операции на множествах с помощью рассуждений.
В пункте в) дети встречаются с ситуацией поиска объединения двух множеств, одно из которых равно подмножеству другого – объединение всегда равно множеству с большим числом элементов.
Ответ:
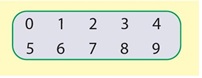
а)
б)
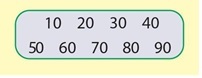
в)
Задача 102. Данная задача решается по той же схеме, что и задачи 95 и 99, которые мы подробно обсуждали. Однако здесь у ребят могут возникнуть проблемы с размещением элементов на схеме. Заготовку для схемы с множествами дети найдут на вкладыше тетради проектов.
Для начала напишем рядом с именами множеств то, что нам известно из задачи: в множестве Ф – 12 элементов, в множестве Б – 16 элементов, в объединении множеств Ф и Б – 20 элементов. Теперь посмотрим на схему внимательно: в объединении 20 элементов, в множестве Ф 12 элементов, значит в той части множества Б, которая остается от пересечения, должно лежать 8 элементов. Всего в множестве Б при этом 16 элементов, значит, в пересечении множества Ф и Б лежит тоже 8 элементов.
Ответ: сразу в двух секциях занимаются 8 человек.
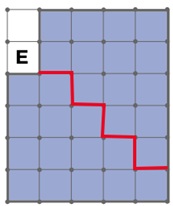
Задача 103. Необязательная. На примере этой задачи дети должны понять, что понятия «равные» и «равные по площади» – это не одно и то же. Действительно на листе определений «Площадь многоугольника» написано, что равные фигуры имеют равные площади. Но, конечно, не всякие фигуры, имеющие равные площади, равны. В частности, чтобы построить две фигуры одинаковой площади, достаточно составить их из одинакового числа клеток. Поэтому в задании а) решений много – подойдут любые две фигуры из 14 клеток, которые вместе образуют многоугольник Е. Решение задания б) единственно.
Ответ: б)
Задача 104. Необязательная. Это типичная задача «на сообразительность». Для ее решения достаточно правильно представить себе описанный в задаче процесс и постараться довести его до конца. Большинство ребят наверняка скажут, что Петя выпьет 2 пол-литровые бутылки, то есть 1 литр лимонада, поскольку за каждые три крышки он получает одну полную бутылку, а у него есть 7 крышек. Но сколько крышек будет у Пети после того, как он выпьет лимонад из этих полученных бутылок? Теперь у Пети снова окажется 2 новых крышки и 1 оставшаяся от семи первоначальных. Это значит, что Петя может их снова поменять на полную бутылку. После этого у Пети останется ровно одна крышка, с которой уже ничего нельзя сделать. Таким образом всего он сможет выпить 1,5 литра лимонада.
Задача 105. Сложность этой задачи в том, что элементы – грузинские буквы – для основного числа ребят совершенно незнакомы. Они воспринимаются как закорючки, их нельзя прочитать, поэтому мешки трудно сравнивать. В процессе решения этой задачи сравнивать буквы приходится довольно много. Попробуем как-нибудь уменьшить число сравнений.
Пересечение построить проще, чем объединение, с этого и начнем. Ищем все общие элементы R и Q, находим пересечение этих множеств – множество В.
Сосчитаем число элементов в объединении R и Q, используя известное теперь число элементов в пересечении. В пересечении 3 элемента, в множестве R от пересечения осталось 2 элемента, в множестве Q – 3 элемента. Получаем, что в объединении множеств R и Q должно быть 8 элементов. Значит, множества Е и Н заведомо не подходят, будем проверять только множества F и G. Видим, что F содержит элементы, которых нет ни в R, ни в Q. Остается теперь только проверить, что множество G нам подходит.
Ответ:
а) множество G равно объединению множеств R и Q;
б) множество В равно пересечению множеств R и Q.
Задача 106. Повторение темы «Площадь прямоугольного треугольника». Площадь прямоугольного треугольника равна половине площади соответствующего прямоугольника. Так, если площадь треугольника 7 ½ ед. кв., то площадь соответствующего прямоугольника должна быть 15 ед. кв. (например, подходит прямоугольник 3´5). У кого-то из ребят могут возникнуть проблемы с заданием б), поскольку 17 – простое число. Есть только один прямоугольник с такой площадью: 17´1.
Задача 107. Необязательная. Сложная задача, предназначенная для сильных учащихся. Как и многие необязательные задачи, эта задача находится на пересечении информатики и математики – к ней применимы методы обеих дисциплин.
Если подходить к этой задаче с точки зрения математики, то для ее решения следует составить уравнение. Примем исходное число за х. К нему приписали слева 3. Это значит, что число увеличилось на 3000, по условию оно при этом увеличилось в 9 раз. Значит, получаем уравнение: х + 3000 = 9х.
Однако, в 5 классе дети еще плохо составляют уравнения, а переносить слагаемые из одной части в другую чаще всего не умеют. Поэтому мы предлагаем применить к этой математической задаче наши обычные методы, например, метод проб и ошибок. Возьмем наугад любое число и проделаем с ним то, что описано в условии задачи. Например, возьмем число 500 и припишем к нему слева 3, получилось 3500: число увеличилось в 7 раз, значит, это число нам не подходит. Попробуем взять число меньше, например 300 и 400. Постепенно мы понимаем, что число 300 слишком маленькое, при приписывании 3 оно увеличивается в 10 раз, а число 400 слишком большое (оно увеличивается в 8,5 раз). Итак, искомое число больше 300, но меньше 400. Добавим также, что последняя цифра этого числа не может быть любой, ведь по условию задачи при умножении числа на 9, в конце числа-результата должна получаться та же цифра. Поэтому последняя цифра либо 0, либо 5. Подходящих чисел теперь всего 19. Их можно перебрать или попробовать ограничить сверху и снизу методом проб и ошибок, как мы это уже делали на уровне сотен. В результате находим искомое число – 375.
Задача 108. Эта задача довольно важная, поэтому мы просим решить ее в классе. Площадь любого многоугольника на сетке можно найти двумя способами: сложением, разбив его на подходящие части или вычитанием, достроив его до прямоугольника. Дети тяготеют к первому способу. Однако в некоторых задачах достраивать многоугольник гораздо удобнее, чем разбивать на части. В этой задаче нам важно, чтобы дети не просто решили задачу именно вторым способом – достроив многоугольник Ц до прямоугольника. Если кто-то из ребят не догадается до такого способа, обсудите задачу вместе.
Итак, рассмотрим прямоугольник П 5´3 клетки, который полностью содержит в себе многоугольник Ц. При этом многоугольник Ц получается, если от прямоугольника П отрезать прямоугольный треугольник Т площадью 1´2 : 2 = 1 клетка. Значит, площадь Ц равна разности площади П (15 ед. кв.) и площади Т (1 ед. кв.) – это 14 ед. кв.
Задача 109. В этой задаче ребятам предстоит построить объект по описанию, которое представлено набором истинных и ложных утверждений.
Прежде всего, все утверждения из таблицы должны иметь смысл. Для этого в последовательности должны быть буквы: К (одна), Ь (один), Н (одна). Из истинности утверждения Е следует, что еще должны быть две буквы А и одна буква З.
Из истинности утверждения С следует, что в искомом слове имеется участок К – … – … – … – Н, который состоит из пяти букв.
Из ложности утверждения D следует, что мягкий знак стоит позже буквы Н. В слове всего 6 букв, поэтому получаем такой «каркас» последовательности:
К – … – … – … – Н – Ь
На оставшихся местах должны стоять две буквы А, и буква З. Из истинности утверждения А следует, что перед каждой А должна стоять согласная, значит буквы должны стоять в таком порядке:
К – А – З – А – Н – Ь
На всякий случай проверим не использованное утверждение В – оно должно быть ложно для нашего слова. Это так.
Ответ: слово КАЗАНЬ.
