Компьютерное дополнение к курсу Информатика 5. 2024

Урок 12. «Утверждения о каждом элементе»

Все, каждый

Понятие все является одним из наиболее важных понятий математической информатики, с которыми ученики знакомятся в нашем курсе. В логике это называется квантором всеобщности. Мы начинаем использовать понятия все, каждый в задачах с самых первых уроков, не вводя их предварительно отдельного на листе определений, так как эти понятия в обычном языке используются детьми практически в том же значении, что в информатике и математике.

Однако не всегда понятия все, каждый казались людям простыми. Например, постижение силлогизмов Аристотеля составляло существенную часть средневекового высшего образования. Возможно, вы встречали и примеры силлогизмов вроде: 

Надеемся, что ученики без труда смогут в будущем строить рассуждения такого рода. Но предостерегаем вас от игнорирования того, что понимание детьми таких «очевидных» слов, как, например, каждый, поначалу может немного или даже существенно отличаться от вашего.

Слова все, каждый всегда относятся к некоторой совокупности объектов. Иногда эта совокупность устроена сложно: все атомы во Вселенной, или все действительные числа. Мы довольно долго будем иметь дело с простыми совокупностями (множествами), умещающимися на одной странице, где объекты сравнительно легко перебрать по одному.

Именно такой перебор (по одному) и нужно осуществлять каждый раз, когда мы выполняем какое-то действие или проверяем какое-то свойство для всех объектов. Не надо формулировать это в виде правила. Лучше, если дети будут относиться к словам все, каждый просто как к словам русского языка с очевидным смыслом. Однако желательно проверить, все ли дети (опять все!) правильно понимают этот смысл и действительно в какой-то мере систематически просматривают все объекты. Это очень важно для формирования информатического, конструктивного взгляда на понятия и процессы.

С другой стороны, в математике и информатике понятие каждый имеет некоторые нюансы, на которые мы хотим обратить внимание. С научной точки зрения термин каждый можно употреблять по отношению к любому числу элементов: как к нескольким элементам, так и к одному. Более того, термин каждый можно употреблять даже с случае полного отсутствии указываемых элементов – и при этом утверждение будет истинным! Например, утверждение «Все крокодилы, которые водятся в Москве-реке – красные» оказывается истинным. Поскольку пятиклассникам эту ситуацию понять будет сложно, мы старались такие случаи в курсе не затрагивать.

Утверждения о каждом элементе последовательности

На данном листе определений рассматривается употребление термина каждый совместно с новой лексикой, относящейся к последовательностям – перед каждой и после каждой. На примере утверждений о последовательностях идея перебора становится действительно осязаемой и легко реализуемой: члены последовательности упорядочены, поэтому удобно и разумно перебор осуществлять в этом же порядке.

Например, нам нужно определить истинность утверждения «Следующая бусина после каждой желтой – красная» для некоторой последовательности. Двигаемся от бусины к бусине, начиная от начала последовательности, пока не дойдем до элемента с заданным свойством (желтую бусину). Найдя такую бусину, проверяем выполнение для нее условия (проверяем, красная ли бусина стоит следующей после нее). Если это условие выполнено – идем дальше по членам последовательности, ищем желтые бусины дальше. И так до конца последовательности. Если оказалось, что условие выполнено для каждой желтой бусины – то данное утверждение истинно. Если условие не выполнено хотя бы для одной из желтых бусин – утверждение ложно. Если условие неприменимо хотя бы к одной из желтых бусин (например, одна из желтых бусин стоит последней, и следующей бусины после нее нет) – утверждение не имеет смысла. 

Задача 64. Эта задача на понимание материала листа определений. В частности, в ней встречаются случаи употребления понятий перед каждой и после каждой для одного элемента и утверждения, не имеющие смысла. Утверждение Ч3 не имеет смысла, потому что после (единственной) буквы А в слове W нет следующей буквы. Утверждение Ч5 не имеет смысла, потому что в слове W нет второй буквы после буквы К, стоящей на шестом месте. Хорошо бы закончить решение этой задачи подробной проверкой, в ходе которой учащиеся опишут для каждого утверждения процесс перебора и обоснуют свой ответ. Например, так «Утверждение Ч1. В слове W две буквы У, предыдущая буква перед каждой У – буква К, значит утверждение истинно», «Утверждение Ч7. В слове W две буквы У (на втором и четвертом местах), следующая после одной У (которая на втором месте) – буква К, а после другой У (которая на четвертом месте) – не К, значит утверждение ложно».

Ответ: утверждения Ч3 и Ч5 не имеют смысла для последовательности W. Утверждения Ч1, Ч2, Ч4 истинны для W. Утверждения Ч6 и Ч7 ложны для последовательности W.

Задача 65. Данная задача начинает серию задач на построение последовательности из элементов заданного множества. Перейдя в курсе 5 класса от понятия мешок к понятию множество, мы потеряли возможность формулировать задачи таким образом: «Построй из бусин мешка последовательность…», так как в общем случае набор бусин последовательности множеством не является (он является именно мешком). Поскольку взаимно однозначного соответствия между набором элементов множества и набором элементов последовательности теперь в общем случае нет, то мы вынуждены использовать более гибкую формулировки:

«Каждая бусина из последовательности А есть во множестве Б» – для построения последовательности берутся только те бусины, которые есть в множестве, причем каждая бусина из множества может встретиться в последовательности и несколько раз, в том числе и вообще не встретится;

«Каждая бусина множества Б встречается в последовательности А» – для построения последовательности берутся все те бусины, которые есть в множестве, причем каждая бусина из множества может встретиться в последовательности и несколько раз, при этом в последовательности могут быть и другие бусины, не из множества.

В данном случае надо построить последовательность только из элементов множества Т, взятых по 1 разу и наша задачи сводится к тому, как эти элементы правильно расставить. В таких задачах полезно использовать метод «проектирования снизу», то есть сбор общего решения из частичных. Заключается он в том, чтобы сначала найти несколько частичных решений – участков последовательности, для которых выполняются некоторые из данных условий, а затем собрать эти участки в одну последовательность так, чтобы выполнялись и все остальные условия описания. Это оказывается не слишком сложно – анализируя утверждения П2 и П1 можно выделить в этой последовательности два участка бусин:

Так как всего в последовательности должно быть 5 бусин, что этими двумя частями и придется ограничиться. При этом цвет круглых бусин в этих частях условием не определен, и порядок этих участков в последовательности тоже может быть любым. Таким образом, данная задача имеет ровно 4 решения, из которых учащемуся необходимо указать хотя бы два.

Задача 66. Постепенно дети знакомятся с разными способами описания последовательности – это может быть просто перечисление элементов, может быть совокупность нескольких условий или общее правило, которому подчиняются все члены последовательности. Вид описания определяет способ построения последовательности – построение, начиная с любого члена, построение начиная с начала, сбор последовательности из частей и т. п. В данной задаче дети впервые сталкиваются с индуктивным описанием последовательности: при таком способе указывается первый член последовательности и правило связи каждого из последующих членов последовательности с его предыдущим (или несколькими предыдущими). Пользуясь индуктивным описанием, мы можем строить последовательность только одним способом – по порядку, начиная с первого члена. Вот одна из последовательностей-решений А:

Для выполнения второй части задания нужно сообразить, что последовательность совершенно точно будет другой, если взять в качестве первого члена другое число. Поэтому разных последовательностей в этой задаче можно построить столько, сколько существует однозначных чисел больших пяти, то есть ровно 4.

На инструкцию в данной задаче можно посмотреть и с другой точки зрения –как на программу для исполнителя (учащегося). Чтобы выполнить эту программу, ребенок должен понимать логические конструкции двух видов – «делай пока» и «если – то». Действительно, ребенок будет работать по этой инструкции, возвращаясь снова и снова ко второму пункту до тех пор, пока длина последовательности не станет больше 6. С другой стороны, второй пункт инструкции представляет собой условный оператор – если условие выполняется, то «находи член последовательности по правилу», если нет – «переходи к следующему предложению или возвращайся к началу пункта 2». Таким образом, задача является пропедевтической для изучения базисных основ программирования, которое детей ждет впереди в нашем курсе.

Задача 67. В данном случае линия разреза является для фигуры Б осью симметрии. Поскольку люди обычно хорошо выделяют ось симметрии на интуитивном уровне, думаем, проблем с решением этой задачи у ребят не будет.

Ответ:

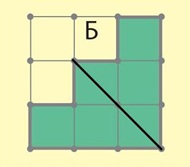
Задача 68. Утверждения в задаче подобраны так, чтобы учащиеся обратили внимание на особенности последовательности М. Утверждение Т2 не имеет смысла, так как перед первым однозначным числом нет предыдущего, а остальные утверждения в задаче истинны.

Задача 69. Это первая задача, в которой необходимо построить объект по таблице истинности, где есть как истинные, так и ложные утверждения (и все утверждения при этом должны быть небессмысленными для построенной последовательности). Поэтому не для всех ребят задача будет легкой, возможно кому-то придется помочь.

При решении этой задачи, как и при решении задачи 65, будем использовать метод «проектирования снизу» – найдём сначала несколько участков последовательности, для которых выполняются некоторые из данных условий, а затем соберем эти участки в одну последовательность так, чтобы выполнялись и все остальные условия описания. Из утверждений А и D, которые должны быть истинными, мы понимаем, что в искомой последовательности есть три участка «3 – 2».

Утверждение С должно быть ложным. Это означает, что длина последовательности должна быть не больше 7. Таким образом, в последовательности либо 6 цифр (три пары «3 – 2») либо 7 цифр (три пары «3 – 2» и еще одна цифра, не равная 3 (по утверждению D должно быть всего 3 цифры 3). Меньше шести цифр быть не может – это мы выяснили на предыдущем шаге рассуждений.

Чтобы утверждение В имело смысл, первой цифрой в последовательности не должна быть 3. Значит, вариант из 6 цифр (трех пар «3 – 2») не годится, в последовательности должно быть 7 цифр: какая-то первая (не равная 3) и вслед за ней друг за другом три пары «3 – 2». Чтобы утверждение В было ложным, первая цифра не должна быть равной 2. Например, вот одно из подходящих чисел: 1323232. Первой цифрой искомого числа может быть не только 1, но и другие цифры (но не 3, не 2 и не 0 – иначе эта последовательность цифр не будет числом), то в этой задаче всего 7 решений.

Задача 70. Необязательная. Здесь тоже можно попробовать собрать последовательность из частичных решений. Из первого утверждения следует, что в искомой последовательности есть участки вида:

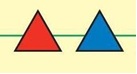
Учитывая заданную длину последовательности, таких участков может быть не больше четырех. Из второго утверждения следует, что 4 таких участка можно просто стыковать между собой и получится искомая последовательность. Скорее всего, большинство ребят именно такое решение и построят.

Однако решений в этой задаче много. Действительно, для истинности первого утверждения достаточно и одного участка «красная треугольная – синяя треугольная». Для истинности второго утверждения в последовательности должна быть хотя бы одна непоследняя синяя треугольная и после нее красная треугольная. Например, решением будет последовательность, где первые 5 бусин любые (но не синяя треугольная и не красная треугольная), шестая бусина синяя треугольная, седьмая – красная треугольная, восьмая – синяя треугольная. Таким образом, во всех подходящих последовательностях шестой, седьмой, восьмой члены должны совпадать. Попросите сильного ребенка найти несколько решений.

Задача 71. Необязательная. Комбинаторная задача, – задача того же типа, что и задача 62. Как и при решении задачи 62, здесь поможет таблица. Имена клоунов будут именами строк этой таблицы, детали одежды (рубашка, туфли) будут именами столбцов. В клетках таблицы мы будем писать цвета и все что узнаем о цветах. Лучше всего в таблице писать карандашом, поскольку нам иногда придется стирать и уточнять информацию.

Сначала читая задачу, просто вычленяем из нее всю информацию о цветах одежды клоунов и делаем записи в таблице.

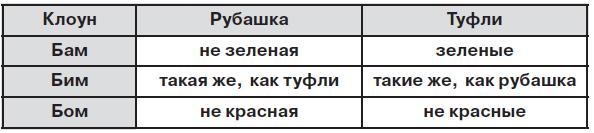
Теперь начинаем анализировать информацию в таблице, используя метод исключения. Туфли Бома не красные, но и не зеленые, ведь зеленые туфли у Бама, значит туфли Бома желтые. Тогда для Бима остаются красные туфли и, значит, рубашка у него тоже красная. Продолжаем так рассуждать дальше и находим единственный правильный ответ.

Ответ: у Бима туфли и рубашка красные, а у Бома – туфли желтые, а рубашка зеленая.

Задача 72. Эта задача продолжает разговор, начатый в задаче 58. Если там последовательность имен месяцев была задана, то в этой задаче имеется в виду именно непрерывная последовательность дней недели, реальное чередование дней – общепринятые договоренности о календаре. Во всех утверждениях речь идет не о словах, а именно о самих днях недели. Мы предполагаем, что после каждого понедельника идет вторник, а после каждого воскресенья – понедельник, а начала и конца (и соответственно первого и последнего элемента) этот объект не имеет. Таким образом, в обычном языке утверждения о днях недели с конструкцией после каждого и перед каждым всегда имеют смысл. Обсуждать все эти соображения всем классом вам, скорее всего, не придется – ребята и сами поймут, в чем тут дело. Но если у кого-то из детей возникнут затруднения – стоит с ними обсудить этот вопрос.

Ответ: истинные утверждения – K, N, O, P, ложные утверждения – L, M, Q.

Задача 73. Необязательная. Похожие задачи ребята уже решали. Множество С имеет ровно 8 разных подмножеств, шесть из которых даны, а два нужно построить. В таком случае построить множества «методом тыка» не стоит, необходимо хотя бы в некоторой степени провести перебор всех подмножеств. Проще всего это делать по числу элементов в подмножествах – сначала убедиться, что среди данных подмножеств есть пустое, потом перебрать все одноэлементные множества, затем все двухэлементные и трёхэлементное. В данном случае не хватает двух двухэлементных множеств.

Ответ:

Задача 74. Очередная несложная задача на разрезание. Чтобы получить два одинаковых треугольника, этот прямоугольник нужно разрезать по одной из диагоналей. Эта задача является предварительной подготовкой к теме «Площадь прямоугольного треугольника на сетке». Хорошо, если большинство над ней поработает.