Страницы сайта
Текущий курс
Участники
Общее
Тема 1
Тема 2
Тема 3
Тема 4
Тема 5
Тема 6
Тема 7
Тема 8
Тема 9
Тема 10
Тема 11
Тема 12
Тема 13
Тема 14
Тема 15
Тема 16
Тема 17
Тема 18
Тема 19
Тема 20
Тема 21
Тема 22
Тема 23
Тема 24
Тема 25
Методический комментарий для учителя к уроку «Члены последовательности. Когда утверждения не имеют смысла»
Урок 11. «Члены последовательности. Когда утверждения не имеют смысла»
На этом уроке мы снова возвращаемся к последовательностям. Здесь вводятся понятия, связанные с частичным порядком. Члены последовательности упорядочены не только относительно начала последовательности, но и относительно друг друга. Эту мысль ребятам необходимо понять, а также освоить новые понятия: следующий и предыдущий, раньше и позже, третий перед и второй после и т. п. Все эти понятия должны быть знакомы пятиклассникам из окружающего мира. Однако полезно обратить внимание ребят на то, что в обычной речи они иногда употребляются не совсем так, как в нашем курсе. Например, допустимо сказать по-русски: «Первые три дня после болезни…», или «Следующие три месяца…». У нас же все понятия употребляются в одном, строго определенном значении, не допускающем неоднозначности. Поэтому у нас может быть только один первый член последовательности, как и один член следующий член после каждого непоследнего. Это соответствует идее ясного и явного введения правил игры.
Списки и языки программирования
Самые первые компьютеры работали с числами. Их использовали для расчета траектории ракеты, которая должна была точно попасть в столицу предполагаемого противника, или объема сырья в ядерном реакторе, который должен был произвести взрывчатый материал для боеголовки той ракеты, и т. п. В некоторый момент, однако, все больше задач, решаемых компьютерами, стало относиться не к числам, а к текстам, изображениям, звукам. Сегодня обработка текстов и изображений – главное занятие компьютеров.
Чтобы объяснить компьютеру, что делать с текстом, надо было создать специальные языки программирования (язык, на котором человек дает инструкцию компьютеру). Самым знаменитым языком, предназначенными для обработки текстов и записи программ, моделирующих интеллектуальную деятельность человека, стал язык LISP. При его разработке математики и специалисты по компьютерам воспользовались языком, изобретенным математиками еще в 30-е годы ХХ века. (Вообще очень многое из примененного в компьютерной технологии было открыто в математике еще до появления компьютеров.) Основным информационным объектом этого языка были последовательности последовательностей. В языке LISP они называются списками (по-английски lists). Английское слово list вошло и в название знаменитого языка: LISt Processing (в переводе на русский язык – обработка списков). Язык LISP послужил основой для многих систем так называемого искусственного интеллекта, в которых люди пытались поручить машине задачи, например, распознавания изображений (например, как роботу перемещаться в пространстве, брать деталь и обрабатывать ее) и человеческой речи (например, как компьютеру понимать устные приказания человека).
Сегодня персональные компьютеры распознают напечатанный текст, понимают устную речь, играют в шахматы на чемпионском уровне. На многих заводах сегодня число рабочих и техников исчисляется всего десятками, а роботов – тысячами; простейшие роботы, в том числе распознающие изображения, школьники собирают из деталей конструктора Лего. Начинается все это с последовательности последовательностей.
Когда утверждения не имеют смыслаОдна из целей нашего курса – научить детей пользоваться языком, прежде всего русским, родным для большинства тех, кому предназначены наши учебники. При этом среди всех аспектов и видов использования мы выделяем тот, который обычно называется формально-логическим. Частью такого умения является понимание различий между формально-логическим и повседневным использованием языка. Хотя мы и собираемся сейчас обсудить некоторые особенности нашего основного, формально-логического применения языка, но начнем мы с житейских примеров.
Нам часто приходится давать другому человеку (или получать от него) инструкции по поиску каких-то предметов. Например: «Слева от шкафа на тумбочке есть стопка книг. Возьми такую, в красной обложке». Или: «Надо выйти на второй остановке после кинотеатра и спросить, где продмаг. За продмагом стоят две башни, надо их обойти, там будет стройплощадка, в конце – детский садик. Можно обойти его слева, но там грязно. Лучше пролезть в дыру в заборе и пройти прямо через территорию садика до ворот. Они закрыты, но рядом калитка...» И т. п. Одной из проблем, с которой мы при этом сталкиваемся, оказывается невыполнимость тех или иных шагов в инструкции. Она может быть вызвана разными причинами. Например, мы не можем пролезть в дыру в заборе. Однако достаточно важной, общей, неудобной и часто встречающейся ситуацией является другая: например, детского садика в этом месте вообще не оказалось. Эту ситуацию мы сейчас обсудим в информатическом контексте.
При попытке выполнения инструкции мы обнаруживаем, что некоторого объекта нет. Бывает и так, что объектов, отвечающих описанию, несколько. Например, спросив, где продуктовый магазин, мы получаем ответ: «Вам какой нужен? Новый, рядом с почтой, или тот, где винный отдел есть?» Оказавшись в такой по-житейски трудной ситуации, мы используем различные стратегии, привлекая дополнительную информацию, осуществляя перебор вариантов и т. п.
Естественно, в информатике мы также часто сталкиваемся с необходимостью выбора объекта по описанию. Такой выбор возникает как при выполнении инструкций, так и в чисто описательных ситуациях. Например, мы можем сказать: «В последовательности выберем следующую букву после буквы Т» или «Красная бусина в последовательности – круглая». Трудности не возникает, если в последовательности всего одна буква Т или всего одна красная бусина. Что же делать, если заданных описанием объектов несколько или их нет вовсе? Нам нужно договориться заранее и ввести в наши правила игры какое-то соглашение на этот счет.
Одно из возможных соглашений состоит в том, чтобы вовсе не употреблять языковых конструкций, которые могут в какой-то ситуации привести к подобной проблеме. Это довольно распространенный в математике подход. Однако наша задача состоит в том, чтобы научить детей использованию по возможности широкого спектра языковых средств и конструкций. Такая ситуация может возникнуть, например, при решении задач по построению объекта по условиям: ребенок должен осознавать, что условия-утверждения должны быть в первую очень небессмысленными для построенной им последовательности или множества и уже после этого можно говорить о том, что они имеют или не имеют заданного в задаче истинностного значения. Часто подобные проблемы возникают при работе с исполнителями: некорректно данная команда или запрос приводят к ситуации «отказа».
Значит, нам надо не запрещать выражения описанного выше типа, а договориться, как их понимать в конкретных ситуациях.
Итак, утверждение «В этой последовательности следующая бусина после синей круглой – зеленая треугольная» мы понимаем следующим образом: «В этой последовательности встречается только одна синяя круглая бусина, при этом следующая после нее бусина существует и она зеленая треугольная». Таким образом, приведенное утверждение не имеет смысла, если синяя круглая бусина либо встречается в последовательности не один раз, либо вообще не встречается. Также утверждение не имеет смысла, если у синей круглой бусины нет следующей. Утверждение оказывается ложным, если следующая бусина после синей круглой существует, но она не зеленая треугольная.
Аналогичная ситуация с понятием предыдущий. Утверждение «В этой последовательности предыдущая бусина перед красной квадратной – желтая круглая» мы понимаем следующим образом: «В этой последовательности встречается только одна красная квадратная бусина, при этом предыдущая перед ней бусина существует и она желтая круглая». Таким образом, приведенное утверждение не имеет смысла, если красная квадратная бусина встречается в последовательности не один раз (в том числе и вообще не встречается). Это утверждение не имеет смысла и в том случае, если у красной квадратной бусины нет предыдущей. Утверждение оказывается ложным, если предыдущая бусина перед красной квадратной существует, но она не желтая круглая.
Утверждение «В этой последовательности десятая бусина – круглая» не имеет смысла для последовательности длиной меньше десяти: в ней десятой бусины нет.
Проблема бессмысленности может встать и в утверждениях с понятиями раньше/позже. Так, утверждение «В этой последовательности журавль идет раньше гуся» мы понимаем следующим образом: «В этой последовательности встречается только один журавль и только один гусь, при этом журавль идет раньше гуся». Утверждение «В этой последовательности журавль идет раньше гуся» не имеет смысла, если журавль или гусь либо встречается в последовательности не по одному разу, либо вообще не встречается. Это утверждение ложно, если в последовательности есть только один журавль и только один гусь и они идут в другом порядке (журавль позже гуся).
Задача 54. В этой задаче, конечно, особое внимание надо обратить на утверждения, которые не имеют смысла. Хорошо бы по окончании решения послушать объяснения ребят по поводу того, почему то или иное утверждение в этой задаче не имеет смысла.
Утверждение П2 не имеет смысла, потому что в последовательности С нет квадратной синей бусины. Утверждение П5 не имеет смысла, потому что в последовательности С не одна квадратная желтая бусина, а три. Утверждение П7 не имеет смысла, потому что в последовательности С нет двенадцатой бусины.
Ответ: утверждения П2, П5 и П7 не имеют смысла, утверждения П1 и П3 истинны, утверждение П4 ложно для последовательности С. Утверждение П6 – неизвестно, истинно или ложно для последовательности С.
Задача 55. Надеемся, что учащиеся к этому моменту ребята уже понимают, что слово определяется не только набором, но и порядком букв, что слово имеет начало и конец. Теперь можно перейти к общепринятой записи слов, которая позволит значительно сократить время решения задач. С этого момента мы договариваемся писать слова слева направо и не писать значки начала и конца последовательности. При этом начало последовательности будет подразумеваться слева, и крайняя левая буква всегда будет считаться первой. Знак конца последовательности будет подразумеваться справа, и крайне правая буква будет считаться последней.
Это типичная задача на построение объекта по описанию, данному в форме утверждений. Для решения такой задачи сначала полезно изучить все утверждения и принять решение, в каком порядке удобнее их использовать. Хотя в этой задаче не идет речь о бессмысленных утверждениях, тем не менее принятые на листе определений договоренности играют здесь важную роль: теперь детям должно быть понятно, что утверждение истинно только в том случае, если оно имеет смысл. В частности, это означает, что все буквы, о которых говорится в утверждениях, совершенно точно должны быть в искомом слове, при этом буквы Р и П – в одном экземпляре.
Прочитав все утверждения, делаем такие выводы: в искомой последовательности 5 букв, среди них есть буквы: Р, Ц, П, Е. В этой последовательности две буквы Е, поскольку четвертая буква гласная, а вторая и четвертая буквы одинаковые. Значит, искомое слово состоят из элементов: Р, Ц, П, Е, Е, причем буквы Е стоят на втором и четвертом месте. Теперь совсем не сложно найти место для оставшихся букв и получить слово ПЕРЕЦ. Кто-то из сообразительных ребят может сразу придумать слово по буквам, данным в утверждении, слово сразу. В таком случае важно напомнить ему о необходимости проверить истинность всех данных утверждений.
В силу сложившейся в школе практики роль догадки, смекалки и интуиции очень незначительна. Меж тем решение сложных задач и проблем, как правило, начинается на уровне догадки и опирается на интуитивное понимание. Поэтому мы приветствуем всевозможные «инсайты», но при этом очень важно, чтобы ребенок мог свои догадки проверить и обосновать.
Задача 56. В отличие от слова, которое мы определяли как любую последовательность букв, ситуация с числом иная. Дело в том, что не любую последовательность цифр можно называть натуральным числом: в первом значащем разряде натурального числа не должен стоять ноль, а в произвольной последовательности цифр это вполне возможно. Мы употребляем в нашем учебнике понятие «натуральное число» в том же значении, что и в математике. Поэтому с последовательностями цифр мы поступаем аккуратнее. Не каждая последовательность цифр является числом, но каждое число все-таки является последовательностью цифр. Поэтому будет вполне естественно, если дети будут писать натуральные числа так, как они пишут их всегда – слева направо без обозначений начала и конца последовательности и без черточек между цифрами. Строя первую последовательность этой задачи, все дети, видимо, так и поступят.
При этом как минимум одно утверждение (утверждение А) будет для этого числа бессмысленным. Ясно, что чем меньше длина написанного ребенком числа, тем бессмысленных утверждений будет больше.
Во втором задании мы просим ребят построить последовательность цифр, для которой все приведенные утверждения истинны. Подходящих последовательностей много и все они состоят не менее чем из 10 цифр. Как именно записать эту последовательность – с использованием знаков начала и конца или просто как число – записанные подряд цифры слева направо – не важно. Важно только, чтобы ребенок хорошо понимал, где начало этой последовательности и где ее конец.
Задача 57. В условии этой задачи не упоминаются бессмысленные утверждения, однако для ее решения необходимо понимание этого вопроса. В частности нужно иметь в виду, что для истинности утверждения необходимо, чтобы оно имело смысл, а в задаче есть примеры последовательностей, для которых утверждение Y не имеет смысла. Утверждение Y имеет смысл только для тех последовательностей, в которых есть ровно одна синяя квадратная бусина и ровно одна красная бусина. Для последовательностей Б и Ж утверждение бессмысленно, потому что в них нет синей квадратной бусины. Для последовательности З утверждение не имеет смысла, потому что в ней нет красной бусины, а для И – потому что в ней две красные бусины.
Ответ:

Задача 58. В этой задаче ребята впервые работают с последовательностью последовательностей, а именно, с последовательностью слов. Такие последовательности удобнее записывать сверху вниз.
Поскольку данная последовательность – это последовательность имен месяцев года, то эта задача может стать поводом для очень интересного разговора о словоупотреблении в нашем курсе и в языке. Действительно, в обычной речи утверждения о месяцах имеют свою специфику, основанную на общих договоренностях («презумпциях»), которые позволяют людям понимать смысл сказанного. Например, обычно подразумевается, что в утверждении идет речь о последовательности из 12 подряд идущих месяцев года, что чередование месяцев – процесс циклический, поэтому последовательность из 12 месяцев можно начинать с любого месяца, хотя чаще начинают с января. Таким образом, в каждом утверждении имеется в виду последовательность месяцев, расположенных в естественном порядке, в которой все месяцы встречаются ровно по 1 разу. Поэтому в обычной речи обычно все утверждения о месяцах имеют смысл. В наших задачах, конечно, мы должны добиваться однозначности понимания условия, поэтому в каждой задаче мы стараемся всегда четко указывать, о какой последовательности идет речь.
Для последовательности месяцев П утверждения В и D не имеют смысла, поскольку слово НОЯБРЬ в ней встречается дважды.
Ответ: утверждения В и D не имеют смысла, утверждения А, С, F, G, H истинны, утверждения E и J ложны для последовательности П.
Задача 59. В данной задаче ребята встретятся с ситуацией, когда выполнение одного из условий влечет за собой выполнение другого, то есть, по сути, добавление одного из условий никак не влияет на решение. Так ясно, что все числа большие 10 и меньшие 21 являются двузначными, поэтому пятое условие ничего нового по сравнению с четвертым и шестым не добавляет. В учебных ситуациях избыточных условий в задачах обычно стараются избегать. Однако мы считаем, что дети должны быть знакомы и с такими ситуациями, равно как и с ситуациями, когда условия противоречат друг другу (и тогда множество решений пусто).
Условия в задаче в основном описывают члены последовательности, и нет ни одного условия, относящегося к порядку этих членов. Поэтому решений здесь будет достаточно много – подойдет любая последовательность из чисел 11, 13, 15, 17, 19, взятых по одному разу.
Задача 60. Необязательная. Все, что было сказано в задаче 58 об утверждениях, касающихся последовательностей месяцев (в обычном языке и в нашем курсе) полностью относится и к последовательностям дней недели. В этой задаче строится последовательность имён дней недели не в календарном порядке, а в другом порядке – удовлетворяющим условия задачи. Для нас последовательность имен дней недели является только списком слов.
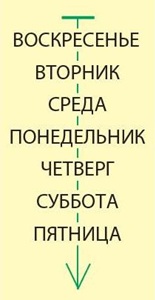
Анализ утверждений в этой задаче – дело не слишком легкое. Поэтому важно выбрать порядок, в котором проще использовать данные утверждения. Начать при этом следует с таких утверждений, которые дают однозначную и определенную информацию. Длина последовательности и условие, что все слова в этой последовательности разные дает нам возможность утверждать, что в этой последовательности все названия дней недели встречаются ровно по одному разу. Из первого утверждения ясно, что первое слово последовательности – ВОСКРЕСЕНЬЕ. Из оставшихся утверждений наиболее определенную информацию дают пятое и шестое утверждения: есть ровно одно имя дня недели из 5 букв– СРЕДА. И имя дня недели, состоящее из стольких же букв, что и ВОСКРЕСЕНЬЕ, тоже только одно – ПОНЕДЕЛЬНИК. Значит третье слово последовательности – СРЕДА, а четвертое – ПОНЕДЕЛЬНИК. Дальше можно использовать четвертое и последнее утверждение, ведь у нас осталось ровно два слова с согласной на конце – ВТОРНИК и ЧЕТВЕРГ, из них только в одном есть две одинаковые гласные. Значит второе слово последовательности – ВТОРНИК, а пятое – ЧЕТВЕРГ. Теперь используем второе утверждение задачи и получаем единственную возможную последовательность.
Ответ:
Задача 61. В этой задаче ребята будут строить множества чисел по описаниям. Пока описания не сложны – включают в себя не больше двух условий. Обратите внимание на задание пункта г). Это как раз тот случай, когда два условия описания противоречат друг другу, так как трехзначных чисел меньше 98 не существует. Поэтому решением в этом задании будет пустое множество.
Ответ:
а) 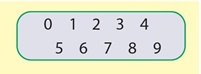
б) 
в) 
г) 
Задача 62. Необязательная. Эта задача открывает серию комбинаторных задач. Она перекликается с основным потоком задач, поскольку здесь тоже необходимо сопоставить несколько условий друг с другом. Такие задачи удобно решать с применением таблицы, куда можно заносить собранную информацию. Нарисуем таблицу, в пустых клетках которой мы будем ставить плюс, если условие задачи позволяет, сказать что человек с такой фамилией увлекается данным занятием, и будем ставить минус, если – точно не увлекается.
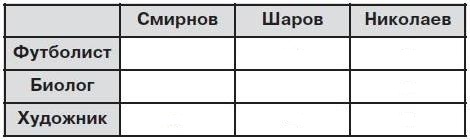
Николаев старше биолога, значит Николаев не биолог – ставим на пересечении строки «Биолог» и столбца «Николаев» минус. Николаев не футболист, так как футболист самый младший из друзей – ставим на пересечении строки «Футболист» и столбца «Николаев» минус. Поскольку Николаев учится в одном классе с сестрой Шарова, значит Шаров не футболист, потому что у футболиста нет ни братьев, ни сестер – ставим на пересечении строки «Футболист» и столбца «Шаров» минус. Теперь из таблицы становится ясно, что Николаев – художник, ставим в соответствующей клетке плюс (мы использовали метод исключения: Николаем не футболист и не биолог, значит он художник, других вариантов нет). Сразу же можно поставить минусы во все оставшиеся клетки последней строки, ведь художник из троих только один и мы его уже нашли.
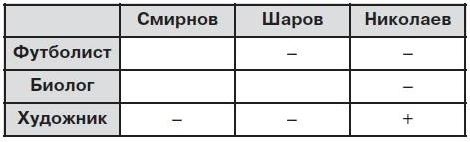
Так, методом исключения продолжаем заполнять таблицу дальше и находим единственный правильный ответ.
Ответ: Николаев – художник, Шаров – любитель биологии, Смирнов – любитель футбола.
Задача 63. Необязательная. Ответ: фигурка с номером 4 такая же, как фигурка с номером 17.
