Страницы сайта
Текущий курс
Участники
Общее
Тема 1
Тема 2
Тема 3
Тема 4
Тема 5
Тема 6
Тема 7
Тема 8
Тема 9
Тема 10
Тема 11
Тема 12
Тема 13
Тема 14
Тема 15
Тема 16
Тема 17
Тема 18
Тема 19
Тема 20
Тема 21
Тема 22
Тема 23
Тема 24
Тема 25
Методический комментарий для учителя к уроку «Многоугольники на сетке»
Урок 2. «Многоугольники на сетке»
Ещё один вид элементов нашего курса – многоугольники на сетке. Появление таких традиционно геометрических объектов в нашем курсе может показаться неожиданным. Но многоугольники на сетке – это наглядный пример дискретных структур. Действительно, любой многоугольник на сетке можно разбить на прямоугольники и прямоугольные треугольники. Площадь каждой такой части – либо целое число единичных квадратов, либо число с половиной. Таким образом, площадь любого многоугольника на сетке – либо целое число единичных квадратов либо число с половиной.
Собственно говоря, многоугольники на сетке являются многоугольниками и в геометрическом смысле. Однако мы рассматриваем только такие многоугольники, все вершины которых можно расположить в узлах прямоугольной сетки. Сетка здесь играет роль очень удобного инструмента, позволяющего ребятам решать довольно широкий класс задач – задач на нахождение площади многоугольника, на поиск равновеликих и равносоставленных фигур, на разрезание и др.
Как и любые геометрические объекты на плоскости, многоугольники на сетке мы считаем равными, если они при наложении совпадают. С геометрической точки зрения под наложением здесь понимаются все преобразования на плоскости, которые переводят сетку в себя:- параллельный перенос на ровное число шагов по вертикали и/или горизонтали,
- поворот на угол, кратный прямому,
- симметрия относительно вертикальной или горизонтальной прямой, а также прямой, расположенной под углом 45 градусов относительно сетки,
- симметрия относительно точки – узла сетки.
Практически движения на плоскости выглядят так, как будто мы вырезали многоугольник из листа и расположили на сетке по-другому. В случае параллельного переноса и поворота мы его просто двигаем и вращаем, а в случае зеркальной симметрии – переворачиваем лицевой стороной вниз. Пример двух одинаковых зеркально симметричных многоугольников на сетке показан на с. 11 на последнем рисунке листа определений в левом нижнем углу. Во всех остальных парах один многоугольник можно получить из другого параллельным переносом и поворотом. При определении равенства многоугольников цвет и расположение многоугольника на сетке не имеют значения. Поэтому в пределах одной задачи все многоугольники у нас всегда будут одного цвета. Как и элементам, мы будем давать многоугольникам на сетке имена и использовать имена для записи равенства фигур.
Задача 8. В качестве линий сетки при рисовании многоугольников учащиеся используют линии клетчатой основы своих тетрадей. В качестве узлов – точки пересечения этих линий (в углах клеток). Поскольку на листе определений мы договорились, что цвет многоугольников на сетке для нас совершенно не важен, то многоугольники, которые дети рисуют в своих тетрадях, они могут не раскрашивать.
Ответ: R = P, T = L.
Задача 9. Как и в предыдущей, в этой задаче мы закрепляем понятие «одинаковые» для многоугольников на сетке. При этом предполагается, что вопрос об одинаковости многоугольников во всех этих задачах мы решаем, визуально сравнивая многоугольники попарно. Однако, можно опираясь на информацию листа определений, дать детям более наглядный и очевидный способ убедиться в том, что два многоугольника одинаковые. Для этого нужно взять прозрачную пленку и перенести на нее изображение одного из многоугольников. Затем следует наложить пленку на второй многоугольник. В некоторых случаях пленку придется перевернуть лицевой стороной вниз. Если в конце концов многоугольники совпали, то они одинаковые, если нет – разные.
На листе определений мы не вводили понятия «треугольник», «прямоугольник», «квадрат», дети используют те знания, которые они получили в курсе математики. Важно, чтобы они при этом понимали, что рисуют многоугольники на сетке.
Задача 10. Наверняка многие ребята заметят, что каждый многоугольник в этой задаче – прямоугольный треугольник, длина одной стороны которого (катета) равна 1 клетке. Поэтому треугольники можно сравнивать, считая длину второй стороны прилежащей к прямому углу (катета).
Ответ: Д = О; В = Э.
Задача 11. Здесь используются буквы армянского алфавита.
Армянское письмо было создано армянским просветителем епископом Месропом Маштоцем приблизительно в 406 г. Возникновение армянского письма (как и некоторых других письменностей) было связано с распространением христианства, принятого армянами в 301 г., и необходимостью создания богослужебной литературы на армянском языке. С небольшими дополнениями месроповский алфавит употребляется и в современном армянском языке. Направление письма – слева направо. В настоящее время армянский язык (в котором используется армянское письмо) является государственным языком Республики Армении.
Мы приводим здесь армянский алфавит и показываем, как называются и как читаются (в квадратных скобках) его буквы. Знак ә (шва) обозначает ы-образный звук, который в русском литературном произношении присутствует в первом слоге слова молоко, но в армянском он возможен и под ударением. Армянский звук [х] более глухой, чем русский [х], раскатисто-хриплый. Транскрипционный знак [g] обозначает звонкую пару к армянскому [х], тоже раскатисто-хриплый. Буква h обозначает звук, похожий на украинское произношение буквы г. Значок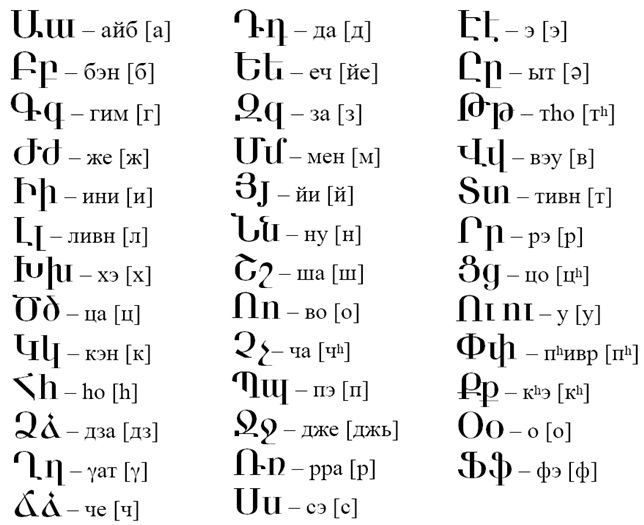
Ответ: ![]()
Задача 12. Ответ: а) У; б) Y.
Задача 13. В этой задаче некоторые многоугольники очень похожи, хоть и не являются одинаковыми. В таких ситуациях снова может помочь наложение многоугольников с помощью прозрачной пленки.
Ответ: В = Н.
Задача 14. Необязательная. Чтобы решить данную задачу, нужно правильно вычленить из условия необходимую информацию. Какая же информация будет наиболее важной для решения задачи? Поскольку оба будильника дают одинаковые звуковые сигналы, то важно догадаться, что если будильники звонят одновременно, Вася, конечно, услышит не 2 сигнала, а только один – может быть он будет громче одинарных, но это для решения неважно. Дальше дело техники – сосчитать, сколько звонков даст каждый будильник и учесть те звонки, которые посчитаны дважды за счет того, что два одновременных звонка Вася слышит как один. Ниже перечислены все звонки каждого будильника от 7.00 до 7.17 (каждый звонок представлен временем, в которое был дан). Курсивом помечены совпадающие сигналы.
Первый будильник: 7.00, 7.03, 7.06, 7.09, 7.12, 7.15
Второй будильник: 7.00, 7.04, 7.08, 7.12, 7.16.
Ответ: Вася услышит 9 звонков: 7.00, 7.03, 7.04, 7.06, 7.08, 7.09, 7.12, 7.15, 7.16.
Задача 15. Необязательная. Это первая задача на разрезание многоугольников на сетке, поэтому она совсем простая. Можно напомнить ребятам, что для многоугольников на сетке цвет не важен, поэтому, перерисовывая фигуру в тетрадь, раскрашивать ее в данном случае не обязательно.
Ответ:
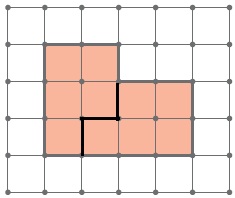
Задача 16. Необязательная. В этой задаче хорошо бы продолжить разговор о знаках дорожного движения, начатый в задаче 7, – дать ребятам задание, выяснить значение каждого из знаков, приведенных в этой задаче, и обсудить, почему водителям и пешеходам важно выполнять требования запрещающих знаков.
Ответ: Е = Р = U. Знак «Поворот налево запрещен».
