Компьютерное дополнение к курсу Информатика 6. 2017

Урок 34. «Выравнивание, решение необязательных и трудных задач»

Задача 235. Эта задача аналогична задаче 46. Решается она стандартным способом – построением дерева перебора всех подмножеств.

Задача 236. Если кто-то из ребят ошибется при построении последовательности, скорее всего, он забыл, что такое среднее арифметическое чисел. Таким детям придется напомнить, что это такое. В данном случае последовательность задана общим правилом, связывающим каждый член последовательности с двумя соседями – следующим и предыдущим (рекуррентное задание последовательности). Поэтому данную последовательность можно строить только с начала – с первого члена. Итак, первый член равен числу 3, второй – числу 7. Из последнего утверждения следует, что второй член равен среднему арифметическому первого и третьего членов (в данном случае просто их полусумме). Получаем уравнение: (3 + х) : 2 = 7, отсюда х =11. Итак, третий член последовательности равен 11. Аналогично находим четвертый и пятый члены. Заметим, что построенная последовательность – арифметическая прогрессия, ведь третье утверждение является необходимым и достаточным условием построения арифметической прогрессии.

Ответ: 3–7–11–15–19.

Задача 237. Необязательная. Это очень полезная для детей задача. Она имеет обобщающий характер и использует дополнительную информацию, которую детям сначала нужно найти в рамках нашего учебника. Это задача на сортировку объектов, критерием сортировки слов является принадлежность входящих в них букв к некоторому языку, которая устанавливается с помощью сравнения букв с буквами-образцами, которые приведены в других задачах учебника. Грузинские буквы ребята смогут найти в задаче 177, армянские – в задаче 104, греческие – в задаче 81. Заметим, что буквы в разных задачах нашего учебника немного по-разному стилизованы, что, в общем, характерно для любого живого языка, ведь даже почерк у разных людей может различаться очень сильно. Поэтому дети в этой задаче могут использовать не только формальное сравнение букв, но и общие отличительные признаки написания букв. Буквы греческого алфавита могут быть знакомы ребятам по урокам математики, например буква π.

Ответ: грузинские слова: 6, 11, 14, армянские слова: 1, 5, 8, 12, греческие слова: 2, 4, 9, 13, еврейские слова: 3, 7, 10.

Задача 238. Строить дерево по набору его последовательностей детям уже приходилось. Однако, если нет никаких дополнительных условий, сделать это можно по-разному. Можно, например, пустить каждое слово в виде отдельной последовательности. В таком дереве каждый родитель будет иметь ровно одного ребенка, поэтому элементов в дереве будет ровно столько, сколько всего элементов во всех последовательностях. В данном случае такой способ явно не годится, ведь в словах всего 45 букв, а в дереве должно быть 23 элемента. Значит, элементы нужно «экономить»: не рисовать одинаковые элементы на одном уровне, если их можно заменить одним элементом. Например, у всех последовательностей дерева одинаковая первая буква – Д, значит, сделаем в дереве А один элемент первого уровня – букву Д. 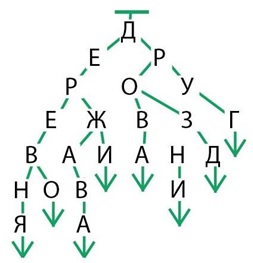Вторые буквы в словах – либо Е, либо Р, значит, у буквы Д будет двое детей – Е и Р. Так будем «экономить» и дальше, в результате как раз получим дерево, в котором ровно 23 элемента:

Задача 239. Простая задача, которую можно предлагать даже слабым учащимся. Решать задачу можно по-разному. Например, сначала строить последовательность по возрастанию, прибавляя семерку к каждому следующему члену. Можно строить и с конца, отнимая семерку от каждого следующего члена. Но сначала надо найти максимальное двузначное число, делящееся на 7. Это 98.

Задача 240. Как видите, задача объемная, но содержательно не слишком сложная. Удобнее всего решать ее, вычеркивая из множества Д все неподходящие числа, анализируя утверждения по порядку.

Ответ: {69, 87, 81, 63, 93}.

Задача 241. Необязательная. Иногда бывает удобно делить все объекты не на две, а на три кучки. Аналогичным образом ситуация складывается и в этой задаче. Разделим все монеты на три кучки и взвесим любые две. Если весы будут в равновесии, значит, фальшивая монета в третьей кучке. Если весы не уравновесятся, то фальшивая монета в более легкой кучке. Итак, за одно взвешивание нам удалось найти кучку из трех монет, в которой находится фальшивая. Вторым шагом будет взвешивание любых двух монет из той кучки, где находится фальшивая монета. Рассуждения здесь будут такими же.

Если монет всего 27, то снова разобьем их на кучки по 3. Таких кучек будет 9. Берем пару кучек и взвешиваем. Если одна кучка перевешивает, то мы нашли кучку с фальшивой монетой. Если весы в равновесии, берем еще одну пару кучек. Таких взвешиваний придется сделать не более 4-х. Если все 4 взвешивания не обнаружили кучку с фальшивой монетой, значит, она в последней кучке. Далее потребуется 1 взвешивание (см. выше). Итого: 5 взвешиваний.

Задача 242. Необязательная. Как и в некоторых других задачах на построение равновесной выигрышной стратегии, характер равновесной стратегии здесь связан с симметрией начальной позиции. Если число лепестков четное, то ромашка является центрально-симметричной фигурой. В такой ситуации для каждого лепестка существует симметричный ему относительно центра, поэтому Второй может повторить любой ход, сделанный Первым. Отсюда вывод: если число лепестков ромашки четное, то выигрышную стратегию имеет Второй. Если число лепестков нечетное, то Первый, оторвав один лепесток, может свести задачу к только что рассмотренной ситуации. Значит, в этом случае выигрышную стратегию имеет Первый.

Задача 243. Возможно, кому-то из ребят придется помогать, поскольку утверждений много и обеспечить их одновременную истинность может оказаться непросто. Элементами нашего дерева могут быть числа 3, 6 и 9. На первом уровне у нас четыре элемента, причем три листа. Все последовательности у нас должны быть разными, значит, все листья первого уровня у нас тоже должны быть разными. Получаем, что на первом уровне у нас 4 элемента – листья 3, 6 и 9 и один элемент, у которого будут дети, например 3. Аналогичные рассуждения мы проводим для каждого уровня. Заметим, что решений в этом задаче несколько, ведь начиная со второго уровня общее число элементов уровня неизвестно (известно только, что листьев должно быть три). Например, на втором уровне может быть один элемент, не являющийся листом, а может быть и три таких элемента.

Задача 244. Повторение алгоритмов для Робота с использованием команды цикл пока. Ясно, что в общем случае Робот должен сначала идти до упора влево, потом до упора вниз, потом до упора влево, и, наконец, до упора вверх. Хотя поля у нас очень похожи, но число клеток в коридорах разное, поэтому здесь можно использовать только команду цикл пока.

Ответ:

Задача 245. Для сообразительных ребят задача окажется довольно легкой. Общее количество участников трех олимпиад – 198. Пусть в одной олимпиаде участвовало Х человек. В двух олимпиадах участвовало в 2 раза меньше, т.е. по количеству «олимпиадомест» это тоже Х. В трех олимпиадах участвовало в 3 раза меньше, чем в одной, т.е. по количеству «олимпиадомест» это тоже Х. Таким образом, разделив 198 на 3, получим число школьников, участвовавших только в одной олимпиаде: 66. Для вычисления двух других групп делим 66 на 2 и на 3, получаем 33 и 22. Всего учеников, участвовавших в олимпиадах по математике, физике и информатике, - 66 + 33 + 22 = 121.

Задача 246. Повторение алгоритмов для Робота. План действий таков. Робот спускается вниз до стены. Движется направо, отыскивая проход. Спускается вниз до упора. Перемещается вправо до упора.

Ответ:

Задача 247. Задача средней сложности на сообразительность. Разделим стопку на две кучки по 4 монеты. Положим на одну чашу весов 4 эталонных монеты, на другую – одну кучку из 4 монет. Если равновесия нет, значит, в этой кучке находится фальшивая монета, в противном случае фальшивая монета находится в другой кучке. Таким образом, мы локализовали фальшивую монету в стопке из 4-х монет. Далее делим эту стопку на 2 кучки по 2 монеты. Берем две эталонные монеты и, как и на первом шаге, сравниваем их по весу с одной кучкой из 2-х монет. В результате находим кучку из двух монет, в которой находится фальшивая. Далее делим эту кучку на две монеты. Берем одну эталонную монету и сравниваем ее по весу с одной из «потенциально фальшивых» монет. Если равновесия нет, фальшивая монета на весах, в противном случае – на столе.

Задача 248. Необязательная. Для детей эта задача может оказаться неожиданной, но идея решения довольно проста. Посчитаем число черных и белых клеток на шахматном поле: 32 белых и 32 черных клетки. В каждой «костяшке домино» одна черная и одна белая клетка, значит, чтобы замостить какую-то часть шахматной доски «костяшками домино», черных и белых клеток в ней должно быть поровну. У нас же вырезаны 2 черные клетки, значит, разбить такую доску на «костяшки домино» невозможно.

Задача 249. Равновесная выигрышная стратегия Первого в этой игре заключается в том, чтобы на первом ходу провести отрезок, который разделит окружность «пополам»: с девятью точками на каждой дуге. Затем каждый ход Второго на одной из дуг Первый будет зеркально повторять на другой дуге.

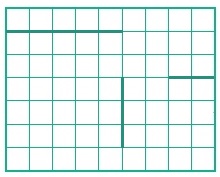
Задача 250. Задачу сильный ученик сможет решить умозрительно. То есть даже без написания программ сможет описать, как должны быть расположены стены. Действительно, Роботу надо сместиться на 6 клеток вниз и на 8 клеток вправо. Алгоритм позволяет шагнуть на 3 клетки вниз, на 3 клетки вправо и на 8 клеток или вниз, или вправо – если нет прохода вниз. Отсюда следует, что с помощью горизонтальной стены мы должны вынудить Робота сместиться вправо на 5 клеток, при этом разрешив спуститься вниз ровно на 3 клетки. Дальше надо проследить, чтобы стены не мешали ему дойти вниз до края поля, а затем – вправо до края поля.

Вот один из возможных вариантов ответа:

Задача 251. Как и в других задачах на перебор вариантов, здесь полезным оказывается дерево перебора. Так как это дерево оказывается слишком большим, лучше не рисовать его, а представить себе, описать, а затем ответить на вопрос задачи. Обозначим людей буквами – А, Б, В, Г, Д, Е, Ж, З. Очередь мы будем строить, конечно, начиная с первого. Тогда первым может быть любой из восьми человек, значит, на первом уровне нашего дерева будет 8 элементов. У каждой из этих элементов 7 детей, ведь вторым может быть любой из оставшихся 7 человек. Значит, на втором уровне 8•7 = 48 элементов. У каждой из этих элементов по 6 детей (48•6 = 288). Так мы описываем дерево вплоть до первого уровня.

Ответ: 8 человек могут встать в очередь 40 320 (=8•7•6•5•4•3•2) способами.

Задача 252. Эту задачу проще решать достраиванием многоугольника Ш до прямоугольника. Заметим, что площадь одного из треугольников (нижнего), которым Ш будет достраиваться до прямоугольника, в свою очередь находится достраиванием (до прямоугольного треугольника), поскольку сам этот треугольник прямоугольным не является.

Ответ: площадь многоугольника Ш равна 9 ½ ед. кв.

Задача 253. Необязательная. Понять закономерности этой игры, как всегда, проще, если сыграть парами несколько партий. Позиций в этой игре всего 12, поскольку в игре никак не учитывается то, сколько кругов обошла стрелка, прежде чем оказалась на данной цифре. Раскрашивать позиции, как всегда, надо начинать с заключительной позиции – 6 (она проигрышная). Далее мы находим все позиции, из которых можно попасть в 6 за один ход (4 и 3) и раскрашиваем их как выигрышные. Теперь следует найти позицию, в результате любых ходов из которой получаются только уже раскрашенные позиции. Это позиция 1, она будет проигрышной. 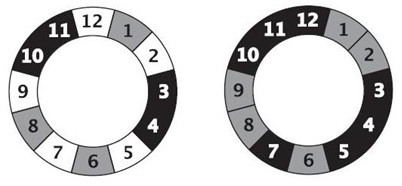Снова ищем позиции, из которой можно попасть только в уже раскрашенные – раскрашиваем позиции 10 и 11 как выигрышные, затем позицию 8 как проигрышную (см. рис. справа). Итак, мы «обошли» один круг, но не все позиции оказались раскрашенными. Придется сделать еще один круг. В проигрышную позицию 8 можно попасть из позиции 5, значит, 5 – выигрышная позиция (позиция 6 уже раскрашена, ее не рассматриваем). Так двигаемся дальше, пока вся числовая линейка не будет раскрашена. Начальная позиция 12 – выигрышная, значит, выигрышная стратегия есть у Первого.

Задача 254. Необязательная. Дети уже видели в нашем курсе много самых разных интересных случаев применения деревьев. Вот еще один такой пример. Здесь от ребят требуется описать с помощью дерева процесс приготовления торта, пользуясь рецептом, который мы приводим в задаче. Итак, элемент первого уровня – торт. Из каких полуфабрикатов он собирается на завершающей фазе приготовления? Из коржей, крема и глазури, значит, это элементы второго уровня (дети элемента «Торт»). Теперь опишем ветки, которые идут от элементов второго уровня. С приготовлением глазури все понятно: дети элемента «Глазурь» – это «Шоколадка» и «Молоко». С коржами не все так просто, потому что приготовление происходит в два этапа. Сначала яйца взбивают с песком, получается пена. Затем пену смешивают с маргарином и мукой. Значит, дети элемента «Коржи» – это «Пена», «Маргарин» и «Мука». В свою очередь, «Пена» – родитель элементов «Сахар» и «Яйца». Конечно, девочки, которые уже занимались приготовлением тортов, наверняка уточнят эту ветку, вставив еще один элемент – «Тесто». Действительно, из сахарно-яичной пены, муки и маргарина сначала получается тесто, а уж потом оно превращается в коржи. Это совершенно верно, но требовать такого «кулинарного» понимания проблемы от всех необязательно. Приготовление крема также идет в 2 этапа, поэтому соответствующая ветка будет иметь длину 3.

Задача 255. В этой задаче слова послания спрятаны в текстах записок без какого-либо порядка, поэтому и найти их несколько сложнее – придется сверять дословно тексты обеих записок. Особую сложность представляют предлоги, которые не так бросаются в глаза. Облегчает задачу только то, что в обеих записках порядок слов в послании сохранен, поэтому можно обе записки сверять сначала в поиске общих слов.

Ответ: «Сбор завтра в девять вечера у старого дерева. Возьми карту и наш план».

Задача 256. При данных условиях у Второго будет равновесная выигрышная стратегия, если на своем первом ходу он продолжит отрезок таким образом, чтобы он разделил поле на две половинки. В дальнейшем надо зеркально повторять все ходы Первого.

Задача 257. Решений здесь, конечно, много. Приведем одно из них:

Задача 258. Необязательная. Это довольно сложная задача, предназначенная для сильных учащихся. Основная ее сложность – догадаться, как здесь применить метод половинного деления. Для начала разделим все алмазы на две кучки по 34 штуки. Теперь будем брать из каждой кучки по одному алмазу и взвешивать алмазы попарно, получится 34 взвешивания. В каждой паре при этом обнаружится более легкий и более тяжелый алмаз. Будем откладывать все более легкие алмазы в левую кучку, а более тяжелые – в правую. В результате после 34 взвешиваний у нас получилось 2 кучки алмазов. Самый легкий алмаз совершенно точно находится в левой кучке, а самый тяжелый – точно находится в правой кучке. Заметим, что левая кучка совсем необязательно содержит только такие алмазы, каждый из которых легче всех алмазов из правой кучки. Но это и неважно, нам важно только то, что самый легкий алмаз находится в этой кучке, упорядочивать остальные алмазы по весу не входит в нашу задачу.

Возьмем левую кучку. В ней 34 алмаза, нужно найти самый легкий. За какое число взвешиваний это можно сделать? Разделим все алмазы снова на две кучки и сравним алмазы из кучек попарно, как мы делали в первый раз. В результате снова получим кучку более легких и кучку более тяжелых алмазов. Вторую кучку можно сразу отложить, она нам больше не понадобится (в ней нет ни самого легкого, ни самого тяжелого алмазов). Итак, мы истратили 17 взвешиваний и получили кучку из 17 алмазов, в которой снова надо найти самый легкий. Отложим один алмаз в сторону, а оставшиеся 16 снова разделим на две кучки и, потратив 8 взвешиваний, найдем кучку из 9 алмазов, среди которых есть самый легкий. Продолжаем процесс дальше – на следующем этапе мы потратим 4 взвешивания и получим кучку из 5 алмазов, среди которых есть самый легкий, и т. д. В результате мы находим в кучке из 34 алмазов самый легкий алмаз за 33 взвешивания.

Заметим, что тот же результат можно было получить без деления алмазов на кучки на втором этапе, а при помощи метода «всплывающего пузырька» (вспомните проект «Сортировки»!). Выложим 34 алмаза (кучка более легких) в последовательность и будем взвешивать соседние алмазы, начиная с конца и менять их местами, передвигая более легкий ближе к началу. В результате одного такого прохода самый легкий алмаз окажется первым в последовательности, и мы потратим 33 взвешивания. Аналогично (только начав взвешивания с начала последовательности), можно поработать с кучкой более тяжелых алмазов и найти в ней самый тяжелый алмаз за 33 взвешивания. Всего мы потратили 100 взвешиваний, как и требовалось в задаче.

Задача 259. Необязательная. На первый взгляд задача кажется довольно сложной, но основная ее сложность – понять условие. Решение при этом заключается в достаточно формальном сопоставлении перечисленных признаков. Составим описание Ивана. Среди описания его дочерей 2 раза встречаются карие глаза, 2 раза каштановые волосы и 3 раза нос с горбинкой. Значит, у Ивана карие глаза, каштановые волосы и нос с горбинкой. Заметим сразу, что и у деда Прохора тоже нос с горбинкой, и переходим к следующему брату. В условии задачи мы не уточняем степень родства внуков Прохора (потому что для решения это не важно). Но если кто-то из детей поинтересуется, почему братья оказываются не слишком похожими, объясните им, что внуки Прохора – двоюродные братья.

Ответ: Иван: карие глаза, каштановые волосы, нос с горбинкой; Степан: зелёные глаза, рыжие волосы, вздернутый нос; Никифор: голубые глаза, русые волосы, прямой нос; Прохор: голубые глаза, рыжие волосы, нос с горбинкой.

Задача 260. Необязательная. Задача достаточно формальная. Требуется занести в таблицу 1 некоторые результаты предыдущей задачи и затем найти значения истинности составных утверждений.

Задача 261. Задача довольно простая, но тут требуется сообразительность. Своим первым ходом Первый должен сделать позицию симметричной. Как это сделать? Сколько камешков взять? Оказывается, надо взять одну (целую) кучу. Затем в точности повторять ходы Второго.

Задача 262. Задача трудна лишь тем, что в одной фразе собраны несколько условий, которые надо использовать параллельно. Итак, начинаем искать нужные числа в пятой сотне. Десятков меньше, чем сотен, значит, во-первых, десятков может быть 3, 2 или 1, а во-вторых – одинаковыми могут быть только две последние цифры (десятки и единицы). Отсюда находим числа: 411, 422 и 433. Рассуждая аналогичным образом, находим числа в шестой сотне: 511, 522, 533 и 544.

Задача 263. Необязательная. Это самая сложная задача на шифровку словами. Поскольку порядок слов в одной из шифровок не сохранен, то придется каждое слово одного послания сравнивать со всеми словами другого послания. Так мы найдем список совпадающих слов (включая и предлоги): ЯВКА, ДЛЯ, В, ДОМЕ, У, ВОДЫ, ПРОВАЛИЛАСЬ, НОВОЕ, МЕСТО, ПОД, КВАРТИРА, ПОД, ДЛЯ, С, ЦВЕТОЧНЫМ, С, МАГАЗИНОМ. Теперь проанализируем порядок основных слов (не предлогов) в обеих шифровках и выберем ту шифровку, в которой порядок слов сохранен (первая). Исходя из порядка основных слов (и их смысла), мы выбираем нужные предлоги и расставляем знаки препинания.

Ответ: «Явка в доме у воды провалилась. Новое место – квартира под цветочным магазином».

Задача 264. Необязательная. Начнем с шифровки конца слова БЕЛЫЙ –

букв ЫЙ, т. к. они шифруются однозначно – СGGАСС. Поищем среди этих символов тройку, которой кодируется буква Г или У, поскольку где-то здесь должна быть зашифрована и концовка слова НОГУ, ведь к шифровке слова БЕЛЫЙ мы можем добавить не больше 3 символов. Действительно, среди этих 6 символов мы находим тройку GGA – код буквы Г. Если в конец этих 6 символов добавить букву А, то мы найдем еще и код буквы У (ССА). Теперь будем двигаться от конца кода к началу. Шифровка слова НОГУ заканчивается так – СGGАССА. Значит мы выбираем такой из кодов буквы О, который заканчивается на С (ТТС). Получаем шифровку букв ОГУ в слове НОГУ – ТТСGGАССА. Тогда конец шифровки слова БЕЛЫЙ – ТТСGGАСС. Значит, нам нужно найти такой код буквы Л, который заканчивается на ТТ. Оба кода АТТ и GТТ нам подходят. Тогда код буквы Н (в слове НОГУ) должен заканчиваться на А или на G. Такой код – GТА. Шифровку слова НОГУ мы уже получили – GТАТТСGGАССА. Теперь подберем к нему подходящую шифровку слова БЕЛЫЙ. Код буквы Е должен заканчиваться на GT – это GGТ. Получаем код слова БЕЛЫЙ – ААСGGТАТТСGGАСС. Теперь видно, что эти две шифровки можно наложить друг на друга (совпадающие части кодов выделены серым). Получается шифровка ААСGGТАТТСGGАССА из 16 символов, в которой одновременно зашифрованы два слова БЕЛЫЙ и НОГУ.

Задача 265. Необязательная. Задача на повторение, предназначенная для сильных учащихся. Здесь ребенок должен сам догадаться, у кого из игроков есть выигрышная стратегия и как ее построить. Ключ к решению этой задачи – конфигурация поля для игры. Действительно, поле 7х7 – центрально-симметричная фигура. Поэтому для каждой его клетки найдется симметричная относительно центральной (по горизонтали и вертикали) клетки. Равновесная стратегия имеется у игрока, который первым сможет занять стратегически важную центральную клетку. Это, конечно, Первый игрок: он должен первым своим ходом раскрасить центральную клетку (4; 4). Дальше Первый будет «уравновешивать» ходы Второго, закрашивая клетку, центрально-симметричную относительно центра поля. Например, если Второй своим ходом закрасил клетку на две левее и на одну выше центральной, то Первый на следующем ходу раскрасит клетку на две правее и на одну ниже центральной. Таким образом, Первый всегда сможет сделать ход, если Второй его сделал. Рано или поздно Второй не сможет сделать следующий ход и проиграет.

Задача 266. Довольно простая задача, рассчитанная на средних и слабых учеников. Предлагать ее всем стоит только в том случае, если вы собираетесь подытожить ее соответствующими выводами, связанными с делимостью. Действительно, построим множество А = {2; 4; 6; 8; 10; 12; 14; 16; 18; 20; 22; 24; 26; 28} и В = {3; 6; 9; 12; 15; 18; 21; 24; 27}. Теперь построим пересечение этих множеств: {6; 12; 18; 24}. Что за числа оказались в этом множестве? Как видим, это все числа меньшие 30, которые делятся на 6. Учитывая то, что числа в пересечении должны делиться на 2 и на 3, можно виде гипотезы формулировать признак делимости на 6. В объединении множеств окажутся все числа, которые делятся хотя бы на одно из чисел – на 2 или 3: {2; 3; 4; 6; 8; 9; 10; 12; 14; 15; 16; 18; 20; 21; 22; 24; 26; 27; 28}.

Задача 268. Необязательная. В этой задаче использовать метод половинного деления не слишком удобно, здесь проще провести следующие рассуждения. Если имеется 2 кольца, одно из которых более легкое, то за одно взвешивание на чашечных весах мы, конечно, найдем более легкое кольцо. А если колец не два, а три, то найти более легкое кольцо тоже можно за одно взвешивание: возьмем два любых кольца и положим их на весы. Если одно из колец более легкое, значит, мы уже нашли то, что искали. Если кольца по весу одинаковые, значит, более легкое – оставшееся кольцо.

Задача 271. Необязательная. В соответствии с методом половинного деления, попробуем для начала разделить детали на две равные по числу кучки и выяснить, в какой кучке деталь, отличающаяся по весу. Следующий вопрос, как это выяснить? Если мы просто взвесим обе кучки на весах, это ничего не даст, ведь мы не знаем, легче искомая деталь или тяжелее. Попробуем иначе – положим на чаши две детали из одной кучи. Если весы будут в равновесии, значит искомая деталь в другой кучке. Если весы не уравновесятся, значит искомая деталь в данной кучке. Итак, после первого взвешивания мы определили кучку из двух деталей, в которой есть искомая деталь. Чтобы выбрать ее, возьмем одну деталь в кучке, где две детали равны по весу. Теперь сравним ее на весах с любой деталью из другой кучки. Если весы уравновесятся, значит, искомая деталь – вторая деталь из кучки с разными по весу деталями. Если весы не уравновесятся, то искомая деталь та, что положена на весы из кучки с деталями разными по весу.

Задача 272. Необязательная. Данная задача – логическая задача, решаемая методом исключения. Такие задачи удобно решать с применением таблиц. Построим таблицу, о которой говорится в условии. В бутылке не вода и не квас, значит, ставим на пересечении первой строки с первым и последним столбцом минусы. Кувшин стоит рядом с лимонадом и далеко от кваса, значит в кувшине не лимонад и не квас. Ставим на пересечении третьей строки и соответствующих столбцов минусы. В банке не лимонад и не вода, ставим на пересечении последней строки и соответствующих столбцов – минусы. Стакан стоит рядом с банкой и далеко от молока. Это значит, что в стакане не молоко и в банке тоже не молоко. Ставим на пересечении второго столбца с соответствующими строками – минусы.

	Квас	Молоко	Лимонад	Вода
Бутылка	―			―
Стакан	―	―
Кувшин	―		―
Банка	+	―	―	―

Теперь проанализируем заполненную по условию таблицу. Из последней строки видно, что квас может быть только в банке, ставим в соответствующей клетке плюс. Из этого следует, что в стакане – не квас, добавляем в таблицу еще один минус. Дальше у нас есть выбор из двух вариантов. Пусть в бутылке – молоко, тогда лимонад в стакане, а вода в кувшине. Теперь пусть молоко будет в кувшине, тогда лимонад в бутылке, а вода – в стакане. Как видим, данная задача имеет два решения. Сильным детям будет полезно найти оба решения, тем более, что с помощью таблицы это будет не слишком сложно.