Страницы сайта
Текущий курс
Участники
Общее
Тема 1
Тема 2
Тема 3
Тема 4
Тема 5
Тема 6
Тема 7
Тема 8
Тема 9
Тема 10
Тема 11
Тема 12
Тема 13
Тема 14
Тема 15
Тема 16
Тема 17
Тема 18
Тема 19
Тема 20
Тема 21
Тема 22
Тема 23
Тема 24
Тема 25
Методический комментарий для учителя к уроку «Биоинформатика. Как кодируются белки»
Урок 30. «Биоинформатика. Как кодируются белки»
В ходе решения задач на шифрование на предыдущем уроке дети подготовились к восприятию данного листа определений. Мы хотели познакомить детей с реальной научной проблемой, но сделать это в доступной для них модели. Моделью в данном случае является шифрование русских слов и текстов тройками латинских букв.
Первая часть листа определений содержит, по сути, повторение – краткое резюме предыдущего листа определений. Думаем, в этой теме такое повторение не помешает. Вторая часть содержит описание того, как происходит кодирование в молекуле ДНК. Оказывается, это происходит так же, как в наших задачах на шифрование. Это главное, что дети должны понять из всех биоинформатических листов определений. Последняя часть листа определений написана в основном для общего развития детей. Скорее всего, кто-то из детей уже слышал в разных контекстах слово «ген» или однокоренные слова. Теперь ребята смогут точно узнать, что это такое. Также дети узнают новое слово «кодон» (у нас в задачах он называется «код»). Кроме того, именно в этом тексте впервые встречается упоминание о том, что в биоинформатике, конечно, не все так просто, как у нас в
задачах на шифрование. Так, в ДНК не вся молекула кодирует белки, а лишь содержащиеся в ней гены. Остальные участки ДНК содержат ничего не значащую информацию, попросту «шум». Значит, ученые, прежде чем расшифровать ДНК, сначала должны выделить в ней гены, а это, как мы увидим на следующем листе определений, не так уж просто.
Этот лист определений является наиболее важным в информатическом плане, к тому же он не слишком большой, поэтому лучше разобрать его на уроке, обсудив со всем классом.
Задача 195. Эта задача совсем простая, она проверяет общее понимание темы урока. Действительно, если шифровка написана верно, то в ней число латинских букв должно делиться на три. Поэтому один из вариантов решения – разделить данный шифр на тройки. Если после последнего целого кода, останется 1 буква, значит, по ошибке вставили лишнюю букву. Если после последнего целого кода останется 2 буквы, значит, по ошибке букву пропустили.
Задача 196. Это довольно сложная задача, как и все задачи на ошибки в шифровании, представленные в данном уроке. В слабых классах их можно просто пропустить. В средних классах есть смысл обсудить основные идеи решения всем классом.
Первые три буквы шифровки ССА – это код буквы У (не Т и не Ш), значит, в первых трех символах уже содержится ошибка. Код буквы Т – ССС, код Ш – СТС. Пусть искомое слово начинается с буквы Ш (ШОК или ШИК). Тогда в первых трех символах пропущена буква Т. Следующие буквы после Ш могут быть – О (код АСТ) или И (код ТАА). Очевидно, вариант с О не подходит, так как в шифровке совсем нет С. Вариант с И тоже не подходит, так как в шифровке с ошибкой нет Т, стоящей после С или через одну (если допустить что первая после С буква вставлена по ошибке).
Пусть искомое слово начинается с Т (ТОК, ТИК или ТАК). Тогда в первых трех символах пропущена буква С (любая из трех). Следующие буквы после Т могут быть О (код АСТ), И (код ТАА) или А (код ААА). Очевидно, вариант с О не подходит, так как в коде совсем нет С. Вариант с И тоже не подходит, так как в шифровке с ошибкой нет Т, стоящей после С или через одну (если допустить что первая после С буква вставлена по ошибке). Запишем шифровку оставшегося слова ТАК – СССААААGG. Если в коде с ошибкой вставить пропущенную С и убрать ошибочно вставленную Т, как раз получается данный код.
Ответ: пытались зашифровать слово ТАК. Его код – СССААААGG.
Задача 197. Эту задачу желательно решить всем учащимся. В процессе ее решения ребята получат новые коды – коды начала и конца предложения (точки). При решении этой задачи дети, естественно, предположат, что все неизвестные им пока буквы – «лишние» тройки, которые служат для маскировки послания или тройки начала и конца, которые нужно определить. На самом деле, как детям позже предстоит выяснить, у нас в шифре вообще нет «лишних» троек – все тройки обозначают какую-нибудь букву или знак препинания. Поэтому данную задачу нужно решать именно на этом уроке, причем до задачи 200, в которой дети впервые сталкиваются с неоднозначностью нашего шифра. Если вы захотите вернуться к данной задаче позже, после решения задач 200 и 206, то она несколько усложнится. Тогда детям придется сначала расшифровать послание целиком, а затем анализировать его с точки зрения осмысленности в рамках русского языка.
В настоящий момент ребята будут решать эту задачу достаточно формально: сначала найдут от начала шифровки все тройки, которых пока нет в таблице расшифровки. Последняя из них будет кодом начала предложения, это тройка CGT. Дальше ребята начнут расшифровку значащей части шифровки и получат слово ПЕХОТА. После этого они встретят 3 незнакомых кода (CTGTCTGAT), а затем снова код начала предложения. Значит, первое предложение состояло лишь из одного слова и в конце этого слова нужно найти код конца предложения, это тройка CTG. Далее расшифровываем второе слово – АВИАЦИЯ и заканчиваем, когда встречаем код конца предложения.
Задача 198. Необязательная. В точности такая задача (и тоже необязательная)
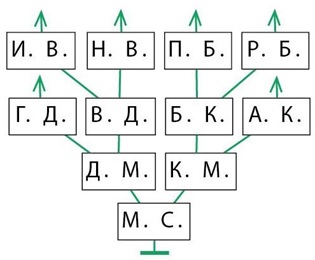
была в курсе 4 класса. По строение родословного дерева Петровых в данной задаче – дело
увлекательное, но отнюдь не простое. Для начала нужно определить, сколько
поколений Петровых будет в дереве. Оказывается, четыре, так как речь идет и о
внуках родоначальника, и о внуках его сыновей. Далее нужно найти
родоначальника. Если в семье Петровых имена (отчества) не повторяются, то это
легко: надо найти человека, отчество которого не встречается как первая буква
ничьих инициалов. Такой человек есть – М. С. Петров (среди оставшихся
Петровых отца мы для него не найдем, значит, он – родоначальник). У него должно
быть ровно два сына, их следует искать по второй букве инициалов (М.).
Таких оказывается, действительно, двое – К.М. Петров и Д.М. Петров.
Далее сыновей каждого из них тоже можно найти по второй букве инициалов и т. д.
В конце необходимо проверить условие о том, что внуков у основателя рода четыре, а у его сыновей – по два.
Ответ:
Задача 199. Необязательная. Сложная задача на ошибки в шифровании, предназначенная для самых сильных
учащихся. Для начала из соображений делимости на 3 найдем, в какой из шифровок
произошла какая ошибка (см. комментарии к задаче 203). При этом выясняется, что
в последней шифровке буквы не хватает, а в предпоследней – лишняя буква.
Сравниваем вторую шифровку с
третьей. Так как в третьей шифровке букву только удалили, значит, все буквы,
находящиеся в ней, – из правильной шифровки и посторонних букв нет. Поэтому все
эти буквы в том же самом порядке встречаются и во второй шифровке. Там, где
этот порядок нарушен, стоит «лишняя» по отношению к третьей шифровке буква: или
лишняя правильная (которая есть в правильной шифровке этого слова), или лишняя
неправильная (которую вставили по ошибке). Начинаем сравнивать две эти
последовательности, начиная с начала. Начала у них совпадают. Так доходим до
буквы G на шестой позиции во второй шифровке – она «лишняя», помечаем ее и
сравниваем цепочки дальше. Следующая такая буква, где последовательности
различаются, – буква С на 9 позиции во второй шифровке, значит, эта буква тоже
«лишняя» по сравнению с последней шифровкой.
Теперь надо понять, какая из букв – G или С – действительно лишняя, а какая правильная. Для этого сравниваем первую шифровку со второй. Теперь мы уже знаем, какие первые три буквы правильные в правильной шифровке – те, где вторая и третья последовательности совпали, а именно ATC. Значит, в первой шифровке в первой тройке есть ошибка. Перебирая варианты, становится ясно, что это удаление буквы, т. е. ошибочное удаление буквы Т. Теперь вставим в первую последовательность удаленную по ошибке букву Т и сравним вторую и третью последовательности еще раз:
AТCAGTCCCAACA
ATCAGGTCCAACA
Видим, что в этих последовательностях совпадают начала и совпадают концы. Выделяя одинаковые отрезки начала (AТCAG) и одинаковые отрезки конца (CCAACA), видим, что «подозрительная» С есть и в первой последовательности на этом же месте, значит, это не ошибка, а ошибочно вставленной буквой является во второй последовательности G. Теперь устраняем ошибку из второй последовательности, затем из первой и расшифровываем слово ПРУД.
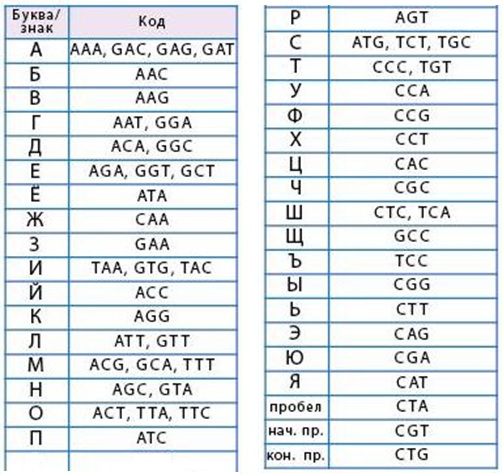
Задача 200. Это важная задача, которую необходимо решить всем учащимся. Здесь дети впервые сталкиваются с неоднозначностью нашего шифра. Действительно, мы на листе определений договаривались, что каждый код мы будем использовать для шифрования только одной буквы (или знака), но при этом одна буква необязательно должна шифроваться только одним кодом. Таким образом, теоретически, имея коды для всех букв и знаков, мы не могли утверждать, что владеем полным шифром. В данной задаче дети практически убеждаются в этом и получают новые коды для русских букв.
Сначала необходимо разобраться, какие шифровки относятся к слову СМЕШНО, а какие – к слову ГЛАДИТ. Поищем сначала такие тройки, которые уже есть в нашей таблице расшифровки. Код буквы Г – ААТ. Это первые три буквы третьего кода, значит, AATATTGACGGCGTGCCC – шифровка слова ГЛАДИТ. Отсюда получаем новые тройки: GAC– код буквы А, GGC – код буквы Д, GTG – код буквы И. Также видно, что первая и последняя шифровка кодируют одно и то же слово, так как у них первые две тройки одинаковые. Оказывается, это слово ГЛАДИТ, так как у обоих слов четвертая тройка кода – GGC. Это код буквы Д. Отсюда получаем новые тройки: GGA – код буквы Г, GTT – код буквы Л, GAG, GAT – коды буквы А, TAC – код буквы И, TGT – код буквы Т.
У двух оставшихся шифровок совпадают четвертые тройки символов – TCA, значит, это шифровки одного и того же слова. Это слово СМЕШНО, так как пятая тройка одного из слов – AGC, код буквы Н. Отсюда получаем новые тройки: TCT, TGC – коды буквы С; GCA, TTT – коды буквы М; GGT, GCT – коды буквы Е, TCA – код буквы Ш; GTA – код буквы Н; TTA, TTC – коды буквы О.
Это таблица со всеми известными на данный момент кодами:
Задача 201. Необязательная. Это одна из немногих задач, имеющая действительно биоинформатический сюжет. Если у вас очень слабый класс и вы решили ограничиться в этой теме только обсуждением шифрования, эту задачу лучше пропустить.
По содержанию эта задача больше относится к математике, чем к информатике – это сюжетная задача на проценты. Тем не менее она оказывается очень полезной в нашем курсе. Далеко не все дети (так же как и взрослые) могут оценить соотношение величин по процентам, часто предложение «Зарплата учителям с 1 января поднимется на 10%» для них не понятно. Для начала нужно приучать ребят переводить такие предложения на понятный им язык. Все сказанное в полной мере относится к листам определений по биоинформатике: необходимо убедиться, что дети действительно понимают, какую часть от всей ДНК составляют гены, и могут ответить на вопрос, сколько это будет в единицах.
Ответ: в генах человека содержится около 90 000 нуклеотидов.
Задача 202. Вот один из вариантов искомого алгоритма:

Обратите внимание, что после выполнения каждого цикла Робот оказывается за пределами раскрашенного прямоугольника и ему надо сделать шаг в обратном направлении.
Задача 203. Эта задача аналогична задаче 197, но несколько проще, ведь теперь тройки начала и конца нам известны, и мы можем легко понять, где начинается и заканчивается каждое предложение, а остальные тройки будут лишними. Основная сложность этой задачи – техническая. Как видите, шифровка очень большая, в ней легко можно запутаться. Не стоит предлагать эту задачу рассеянным, медлительным детям. Поскольку в отличие от задачи 197 предложения здесь состоят не из одного слова, то шифровки слов, как обычно, разделены тройкой, кодирующей пробел.
Ответ: СТЯГИВАНИЕ ВОЙСК НА ЗАПАД ОБМАН. БЕРЕГИТЕ ЮЖНЫЕ ГРАНИЦЫ.
Задача 204. Наибольшую сложность здесь представляет вычисление площади многоугольника З, т. к. его площадь нельзя найти разрезанием. Однако без этого вообще можно обойтись, ведь многоугольники равной площади – А и Г.
Задача 205. Это вторая задача с биоинформатическим сюжетом. По содержанию она несложная. Можно решать ее по-разному, например так. Для начала выберем в последовательности остатки, которые повторяются три и более раз. Таких оказывается три: Н, Т и Р. Теперь для каждого из них выпишем все коды, которые встречаются в данном участке ДНК. Н: CAC; P: СCA, CCG; T: ACA, ACC, ACG. Теперь находим название нужного остатка в таблице на форзаце, это треонин. Полный список его кодов: ACA, ACC, ACG, АСТ.
Задача 206. Это последняя задача на выяснение новых кодов, ее обязательно нужно решить всем учащимся. В каждой из таблиц (шифровки и расшифровки) будут находиться все возможные тройки (в задаче 184 дети выяснили, что таких троек всего 64). Сначала найдем в этих кодах те тройки, которые есть в таблице. Тройка GAG кодирует А, значит, TTGGAGTAT – шифровка слова ПАР. Коды ТТА, АСТ и ТТС шифруют букву О, значит, GGGTTATAT, TGATTCGTT, GTCTTATGG, TATACTTGG – шифровки слов ВОР, РОК, ПОЛ, КОК, соответственно. Тройка ССТ кодирует букву Х, значит, TAGCCTTTC – шифровка слова УХО. GCGTATTCG – шифровка слова ЗРЯ.
Из шифровок слов ПАР, УХО и ЗРЯ получаем новые тройки: TTG – код буквы П, ТАТ – код буквы Р, TAG – код буквы У, GCG – код буквы З, TCG – код буквы Я.
Выясним соответствие между словами ВОР, РОК, ПОЛ, КОК и их шифровками. TATACTTGG – шифровка слова РОК (по букве Р). GGGTTATAT – шифровка слова ВОР (по букве Р). GTCTTATGG – шифровка слова КОК (по последней тройке, которая такая же, как в слове РОК). TGATTCGTT – шифровка слова ПОЛ. Отсюда получаем новые тройки: TGG, GTC – код буквы К; GGG – код буквы В, TGA – код буквы П.
По окончании решения этой задачи мы получаем полные таблицы шифровки и расшифровки.
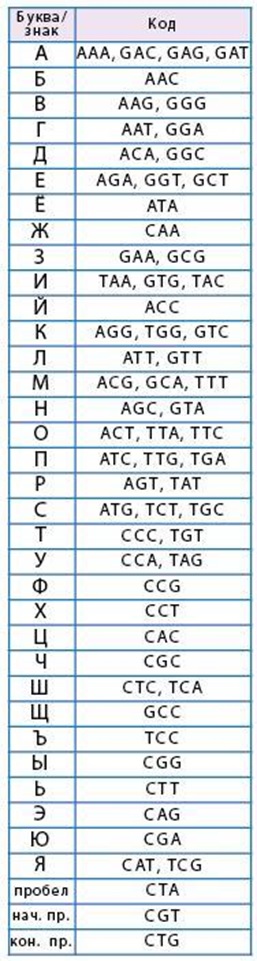
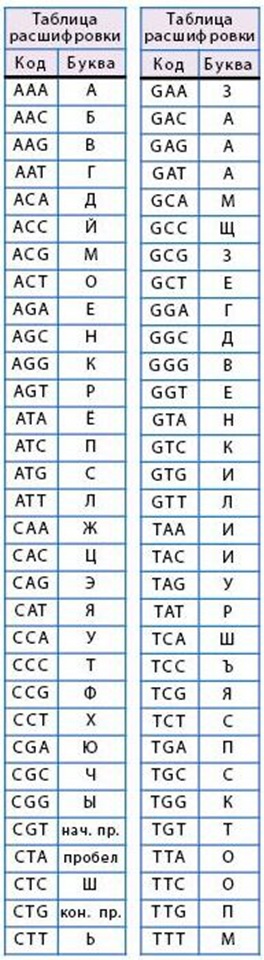
Задача 207. Необязательная. Здесь нерационально делать полный перебор вариантов, кто из гномов правдивый, а кто – лжец. Лучше проанализировать утверждения гномов и найти какую-то подсказку. Такой подсказкой оказываются высказывания Жени. Оба его утверждения либо истинны, либо ложны. Допустим, они истинны, тогда получается, что все остальные гномы – лжецы. Значит, утверждение Вани должно быть ложно, но оно оказывается истинным. Мы пришли к противоречию, значит Женя лжец. Из этого следует, что Саня – правдивый и либо Ваня, либо Даня правдивый. Видно, что правдивый Даня, поскольку именно он называет Женю лгуном, что правда. Значит, Ваня – лгун, поскольку называет лгуном правдивого Даню.
Ответ: Из четырех гномов всегда говорят правду Саня и Даня.
Задача 208. Это довольно сложная задача – как содержательно, так и технически; предназначена она, в основном, для сильных и техничных детей. Ключ к решению в том, чтобы правильно построить модель. Как видим, для приготовления пиццы Марчелло выбирает любые наборы из имеющихся продуктов, это напоминает построение всех подмножеств данного множества. Задача оказывается аналогичной такой: «Сколько существует различных подмножеств шестиэлементного множества (у нас всего 6 продуктов)?». При этом надо учитывать, что Марчелло обязательно добавляет хотя бы один продукт, поэтому пустое множество надо будет отбросить. Для построения множества всех подмножеств мы строим дерево перебора вариантов. Однако здесь оно будет слишком большим, да и все наборы нам по условию описывать не нужно. Поэтому попробуем не прописывать дерево подробно, а лишь представить и описать его. На первом уровне два элемента – «есть перец», «нет перца». После каждой из них снова идут по два элемента – «есть лук», «нет лука», значит, всего на втором уровне 4 элемента. После каждого из них снова идут два элемента – «есть грибы», «нет грибов», значит, на третьем уровне 8 элементов. Продолжая аналогичные рассуждения, получаем, что на четвертом уровне 16 элементов, на пятом – 32, на шестом (последнем) – 64. Итак, в нашем дереве всего 64 последовательности. Значит, у множества исходных 6 продуктов (добавок к коржу и сыру) есть 64 разных подмножества. Теперь нужно отбросить пустое подмножество, и получаем ответ к задаче.
Ответ: Марчелло может приготовить 63 вида пиццы.
