Компьютерное дополнение к курсу Информатика 6. 2017

Уроки 27–28. «Составные условия: слова «и», «или», «не»

И в жизни, и в программировании зачастую бывает удобно использовать не одно условие, а сразу несколько. Например, мы можем дать такую инструкцию ребенку: «Если в доме нет молока или кефира, сходи в магазин». Или: «Если меня дома не будет и ты захочешь есть, достань из холодильника миску с салатом, а хлеб лежит в тумбочке». Точно так же и в программировании – условия могут объединяться словами И, ИЛИ. Такие условия называются составными. Составные условия имеют значения истинности в зависимости от значений истинности входящих в них простых условий. Понять и запомнить, как определяется значение истинности составных условий, представляет наибольшую сложность для детей на этом листе определений.

В учебнике приведены наглядные примеры использования составных условий. Например, как узнать, находится ли Робот в левом верхнем углу поля? Очевидно, надо проверить сразу два условия: сверху стена и слева стена. Если оба условия выполняются, то Робот стоит в левом верхнем углу, если хотя бы одно из условий не выполнено, Робот стоит в другой клетке поля. Таким образом, при использовании составного условия со словом И истинным составное условие будет только в том случае, если истинны оба составляющие его простые условия. Если хотя бы одно из них ложно, ложным будет и составное условие.

Иногда при определении положения Робота для нас не важно, около какой границы поля он стоит, главное – чтобы это была, например, вертикальная стенка. В этом случае удобно соединять условия словом ИЛИ: слева стена ИЛИ справа стена. Если выполняется хотя бы одно из этих условий – значит, Робот стоит около вертикальной стены. При использовании составного условия со словом ИЛИ ложным составное условие будет только в том случае, если ложны оба составляющие его простые условия.  Если же хотя бы одно из них истинно, то и составное условие истинно. На листе определений приведены таблицы истинности для слов И и ИЛИ. В общем и целом новый материал не таит в себе особых сложностей, ибо семантика слов И и ИЛИ близка семантике этих  союзов в русском языке.

К составным относятся также условия со словом НЕ. Если в русском языке слово НЕ может употребляться в нескольких различных значениях, то в программировании оно означает только одно – отрицание первоначального условия. Таким образом, НЕ слева стена означает слева свободно, НЕ справа свободно означает справа стена. И так далее. То есть, приписав к условию слово НЕ, мы меняем его значение истинности на противоположное: истинное условие становится ложным, а ложное – истинным. В этом тоже нет ничего особенно сложного.

Задача 171. Простая задача, позволяющая закрепить новый материал. Если ребенок допускает ошибки, верните его к таблицам значений истинности составных условий на листе определений.

Задача 172. Простая задача о трансформации отрицания. Здесь придется каждое условие заменить на другое, так чтобы значение первоначального условия не изменилось. Например, вместо «не клетка закрашена» напишем «клетка чистая», потому что именно это условие противоположно по смыслу и по значению условию «клетка закрашена». Единственное, что может здесь смутить детей,  – это то, что составные условия со словом НЕ звучат не по-русски. По-русски мы все-таки сказали бы «клетка не закрашена», а в алгоритмическом языке – «не клетка закрашена». Дети могут поинтересоваться, почему такая искусственная конструкция. Объясните любознательным, что НЕ в программировании относится ко всему условию целиком, поэтому не может стоять где-то в середине – только в начале.

Задача 173. Задача на закрепление нового материала несколько более высокого уровня сложности, нежели две предыдущие. По содержанию она обратна задаче 172. Здесь для каждой клетки нужно найти истинное условие. Если ученик пометит все закрашенные клетки единицей, а все незакрашенные клетки четверкой, то это тоже будет правильным решением, хотя часть клеток может быть помечена и другими цифрами.

Задача 174. Необязательная. Это сложная задача по теме листа определений. Здесь нужно найти клетку, принимая во внимание значения истинности трех составных условий. Типичные рассуждения могут быть такими. Найдем клетку с именем А. Согласно первому утверждению, нас устроят как закрашенные клетки (таковых две), так и клетки, где сверху стена (таковых много). Возьмем левую закрашенную клетку. Второе утверждение для нее подходит, а вот третье – нет. Правая закрашенная клетка не подойдет, потому что для нее второе утверждение ложно. Теперь нам придется рассмотреть клетки, где сверху стена.  И так далее. Заметим, что сообразительные дети будут начинать не с первого утверждения, а с последнего, ибо оно сразу ограничивает перебор шестью клетками. Поскольку все они не закрашены, то сверху должна быть стена (1-е утверждение), что сокращает перебор до четырех клеток. 

Задача 175. Закрепление нового материала. Довольно утомительно в полном объеме проводить все 22 цикла. Однако это придется сделать, если ученик не проанализирует внимательно работу одного цикла. Каков результат каждого цикла? Если Робот стоит на чистой клетке и слева свободно, то он свою клетку закрашивает и шагает влево. Если он стоит на закрашенной клетке или слева стена, то он все равно оказывается на 1 клетку левее, но без закрашивания. То есть в конечном итоге положение Робота легко определить простым подсчетом 22 клеток. Что же касается раскраски, то дополнительно будут раскрашены все чистые клетки, кроме тех, перед которыми есть стена.

Ответ:

Задача 176. Необязательная. Сложная задача на сообразительность. Первая мысль, которая, возможно, придет в голову некоторым детям, – нарисовать дерево перебора всех вариантов. Однако, начав рисовать дерево, ребенок очень скоро поймет, что ему не хватит никакой бумаги, чтобы его закончить. Действительно, в результате первой команды у нас получается 2 числа, после второй – 4, после третьей – 8, после четвертой – 16, после десятой – 1024. Дальше счет пойдет на тысячи. Где же уместить такое количество вершин? Так что с деревом ничего не выйдет. Как же быть? Надо подумать. Любая цепочка команд приведет к тому, что результатом будет целое число. Но какое? На какое максимальное число может переместиться Кузнечик? Вперед – на 45 (если все 15 команд будут вперед 3), назад – на 30 (если все 15 команд будут назад 2). Остается вычислить два простых арифметических выражения: 100 + 45 = 145 и 100 – 30 = 70.

Ответ: все числа от 70 до 145 включительно.

Задача 177. Необязательная. Поиск трех одинаковых фигурок. Задача решается полным перебором. Желательно, чтобы дети проводили перебор по какой-нибудь системе (например, слева направо и сверху вниз), а также ставили пометки около просмотренных букв.

Ответ: три одинаковые – буквы . Один раз встречается буква  .

Задача 178. Трудная задача о достраивании алгоритма для Робота. На самом деле решение можно отыскать довольно быстро, надо только задуматься: на первом шаге Робот явно должен обходить препятствие сверху. А в каких условиях он находится в начальном положении? Слева стена и сверху свободно. Проверяем это составное условие для всех шагов по очереди – оно нам подходит. Решение найдено.

Задача 179. Сложная задача на алгоритмы для Робота. Здесь главное – не запутаться в циклах и условных командах, их много, есть вложенные циклы, так что надо быть предельно внимательным.

Ответ:

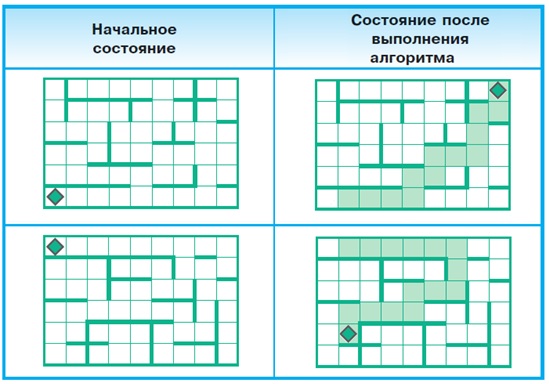
Задача 180. Если ребенок решил предыдущую задачу и разобрался в том, как устроен алгоритм выход из коридора, то он без труда справится с этой задачей. Решений здесь, конечно, много. Главная трудность – чтобы не было отказа во второй части (где Робот должен идти вверх и вправо). Всего он должен сделать 9 шагов, при этом по вертикали – только 6 (т.к. у нас поле 7 х 7), остальные 3 шага надо сделать по горизонтали. Отсюда следует, что в первой части алгоритма Робот должен сделать 3 шага, это определяет длину горизонтального коридора (нижнего). В сущности, одной этой стенки будет уже вполне достаточно. Но, конечно, дети могут нарисовать еще какие-нибудь стены. Лишь бы на каждом шаге у Робота была возможность переместиться либо вверх, либо вправо.

Задача 181. Задача, аналогичная задаче 168. По условию получается, что если одновременно сверху и снизу от Робота нет стен, то Робот находится в вертикальном коридоре, и чтобы выйти из коридора, ему надо продвигаться вверх или вниз. Если же одновременно свободно справа и слева – то продвигаться нужно вправо или влево. Как именно продвигаться – отдельный вопрос. Так как в коридорах есть ответвления, то проверять наличие стены только с одной стороны от Робота, как мы это делали в задаче 168, недостаточно – стены может и не быть из-за ответвления, а Робот при этом еще не вышел из коридора. Надо проверять каждый раз обе стены коридора. Так как по условию, ответвления в коридоре не могут располагаться напротив друг друга, то пока Робот идет по коридору, в каждой клетке у него есть стена либо с одной стороны, либо с другой. Если стен нет с обеих сторон – то это значит, что Робот вышел из коридора.