Компьютерное дополнение к курсу Информатика 6. 2017

Уроки 25–26. «Равновесные выигрышные стратегии»

Рассмотрение равновесных выигрышных стратегий является дополнительной и, в общем, необязательной темой. Если вы работаете с детьми, которые не занимались с нашим курсом в начальной школе, эту тему можно безболезненно пропустить, уделив больше времени основным понятиям темы «Игры». Для детей же, которые в 4 классе уже познакомились с играми с полной информацией, наоборот, равновесные стратегии будут полноценным новым материалом, которому можно посвятить больше времени, быстро повторив основной материал по играм. Итак, к этому уроку дети знакомы с различными играми с полной информацией, умеют исследовать позиции некоторых игр и строить выигрышные стратегии для них. До сих пор мы обсуждали только такие игры, все позиции которых несложно перебрать – исследовать, выигрышные они или проигрышные. Конечно, за рамками этого рассмотрения остались многие игры. Есть и другие способы построения выигрышной стратегии. Даже исследуя простые игры, дети могли заметить, что иногда выигрышную стратегию можно описать, не ссылаясь на раскрашенную числовую линейку или шахматную доску. Например, в игре Камешки, где можно брать 1 или 2 камешка за ход (задача 126), стратегию можно описать просто: оставлять противнику позицию, кратную 3. Другой пример – игра Ладья, которую мы еще раз обсудили на этом листе определений. Здесь тоже, чтобы описать стратегию, не нужно апеллировать к раскрашенному полю, правило можно описать проще: возвращать ладью на главную диагональ. Оказывается, существует довольно много и других игр, выигрышная стратегия в которых тоже может описываться не как подробное правило, перебирающее все возможные позиции игры, а более простым, сокращенным образом. На этом уроке мы будем строить стратегии одного такого «сокращенного» типа, которые будем называть равновесными. Лист определений, посвященный равновесным стратегиям, очень объемный. Знакомство с ним стоит перенести на дом – попросите детей заранее прочитать текст (не только прочитать, но и понять и разобраться с примерами), чтобы на уроке только обсудить непонятные места и ответить на вопросы.

Задача 154. Как всегда, первые задачи после листа определений – это простые задачи, проверяющие то, как дети усвоили материал новой темы. При исследовании игры Шары и ящики дети могут поначалу растеряться – слишком общие правила, количество шаров в ящиках не указано. Обратите внимание таких детей на указание к задаче и попросите для начала рассмотреть игру с каким-нибудь небольшим количеством шариков в ящиках, например, 3 и 3 и 3 и 4. Попросите постараться построить именно равновесную стратегию, ведь эта игра очень похожа на игру Монеты на весах с листа определений (на самом деле это ровно та же игра).

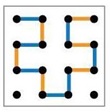
Задача 155. При решении этой задачи проверяется усвоение последней части листа определений – примера с игрой Ползунок. Строить нужную последовательность лучше сначала карандашом, чтобы можно было легко исправить ошибки. Важной частью выигрышной стратегии Первого в этой игре является первый ход: первый отрезок должен быть обязательно поставлен в центре поля. А дальше Первый следует простой равновесной стратегии, так же как в примере на листе определений. Мы приводим один пример такой последовательности из множества возможных:

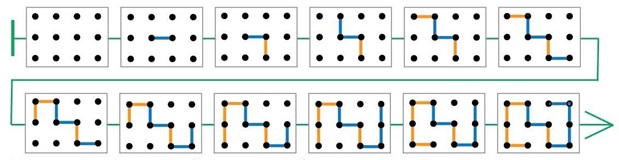
Проверять решение этой задачи вам будет нетрудно: заключительная позиция должна быть симметрична относительно центра поля. Останется только проверить саму последовательность – правильно ли добавлены отрезки на каждом ходу.

Задача 156. Еще одна простая задача, позволяющая лучше усвоить материал новой темы. Затрудняющегося ребенка стоит попросить еще раз внимательно прочитать ту часть листа определений, где обсуждается игра Ладья.

Задача 157. В этой задаче детям предлагается классифицировать числа данного множества в соответствии с остатком от деления на 4. При этом тот факт, что таких групп будет только 4, предоставляется открыть самому ребенку. Собственно, любое множество натуральных чисел можно рассортировать на такие 4 группы (по остатку от деления на 4). Надеемся, что вдумчивых детей эта задача заставит задуматься об этом.

Ответ: остаток 0 – {24, 80, 144}, остаток 1 – {9, 85, 93}, остаток 2 – {10, 46}, остаток 3 – {3, 35, 55, 71}.

Задача 158. Это первая задача в этом уроке, в которой детям предлагается для самостоятельного исследования новая игра. Конечно, в этой игре нужно пытаться строить равновесную стратегию: исследовать все позиции в этой игре затруднительно, а никакой другой способ, кроме построения равновесной стратегии, детям не известен. После решения задачи 165 сильным детям будет нетрудно догадаться, что и в этой игре стратегия должна быть «зеркальной» – Первый первым ходом ставит 1 или 2 плюса в центре (в зависимости от того, четное или нечетное число минусов в начальной позиции). После этого Первому остается только повторять ходы Второго, зеркально отражая их относительно центра позиции.

Детей, которые не смогут сразу догадаться, какой должна быть выигрышная стратегия, попросите выписать строку из 18 минусов, провести вертикальную черту в середине этого ряда и постараться понять, в чем состоит равновесная выигрышная стратегия в этой ситуации.

Задача 159. Игра в этой задаче уже не повторяет примеров листа определений. Но при этом условие задачи само содержит общее описание равновесной выигрышной стратегии. Детям остается лишь понять это описание и построить какую-либо последовательность позиций, в которой Первый следует описанной выигрышной стратегии. На рисунке мы привели одну из возможных заключительных позиций такой партии.

Задача 160. Необязательная. Повторение темы «Пересечение и объединение множеств». Детям предлагается построить два множества, при том что даны объединение и пересечение этих множеств и еще два дополнительных условия.

Из первых двух утверждений следует, что бусины множества П есть и в

множестве А, и в множестве В. Еще в эти множества входят только три бусины – треугольная зеленая, треугольная желтая и круглая желтая. Из третьего и четвертого утверждений следует, что обе желтые бусины лежат в множестве А, а зеленая – в множестве В.

Задача 161. Составление алгоритма для Робота с использованием команды цикл пока. Прежде всего, поставим Робота в какое-нибудь крайнее положение, например в левый верхний угол. Далее нам потребуются четыре команды цикл пока для закрашивания четырех рядов клеток, идущих вдоль сторон прямоугольника. Вот один из возможных алгоритмов:

Задача 162. Необязательная. Повторение темы «Дерево перебора вариантов». На первом уровне дерева будут 4 цифры, у каждой из них – по три цифры, у каждой бусины второго уровня – по две цифры, у каждой бусины третьего уровня – одна цифра.

Задача 163. Задача на построение равновесной выигрышной стратегии в новой игре. Детям необходимо разобраться с правилами игры, понять, как получаются заключительные позиции. При внимательном изучении правил игры становится ясно, что шашки двигаются всегда в одном направлении – к середине поля. Игра заканчивается, когда шашки «встречаются», оказываются на соседних клетках поля. При этом встретиться они могут и не на середине поля: например, один игрок может всегда передвигать свою шашку на две клетки, а другой – всегда на одну.

Тем не менее, пытаясь построить равновесную стратегию, отметим середину поля и посмотрим, что будет, если Второй будет в точности повторять ходы Первого: Первый сдвинет свою шашку на одну клетку – и Второй тоже на одну, Первый на две – и Второй на две. В такой партии после каждого хода Второго шашки будут стоять симметрично относительно середины поля. Значит, когда Первый подойдет вплотную к середине (встанет в 10-ю клетку), то Второй на своем ходу тоже встанет в 10 клетку, считая со своей стороны. Шашки встретятся, игра закончится. Последним сделал ход Второй, значит, он выиграл. Итак, наша стратегия – выигрышная.

Конечно, описание найденной стратегии не у всех детей получится гладким и безошибочным. Поддержите детей, помогите им хорошо сформулировать описание той стратегии, которую они придумали.

Задача 164. Учащиеся уже решали подобную задачу, но с существенно меньшей начальной позицией. Раскрасив фрагмент числовой линейки от 0 до 16, дети приходят к выводу, что выигрышные и проигрышные позиции чередуются по определенной схеме, а именно: кроме 0, все проигрышные позиции кратны 4: 4, 8, 12, 16, … Теперь определим, какой будет начальная позиция. Для этого достаточно выяснить, кратно ли 4 число 308. Число 308 делится без остатка на 4,значит, начальная позиция – проигрышная, то есть выигрышная стратегия есть у Второго. Она состоит в том, чтобы после каждого своего хода оставлять в куче число камешков, кратное 4.

Задача 165. Построение последовательности по описанию.. Из последнего утверждения следует, что в нашей последовательности есть только числа 1, 3 и 4, но не в одном экземпляре (т. к. длина последовательности равна 5). Из второго утверждения получаем, что первый член последовательности – это число 3, а третий – число 1. Теперь для того чтобы первое утверждение было истинным, нужно поставить единственное четное число множества К на остальные места в последовательности. Действительно, следующим после числа 3 и после числа 1 должно идти четное число (а значит, 4). Последний член последовательности тоже не может быть нечетным числом, иначе первое утверждение станет бессмысленным. Значит, и последний член последовательности – число 4.

Ответ: 3–4–1–4–4.

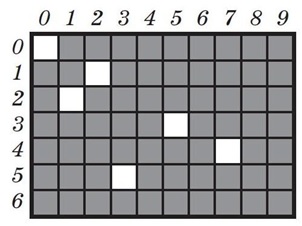
Задача 166. Хотя в этой задаче и не требуется изучать все позиции и раскрашивать таблицу, все-таки лучше это сделать – оказывается, так будет проще решить задачу (составить нужные последовательности позиций). Конечно, можно раскрасить две таблицы – 9х6 и 7х4. Но, если подумать, достаточно и одной, бо́льшей таблицы 9х6, которая полностью включает меньшую. Для быстрой и правильной раскраски таблицы нужно хорошо понять правила игры и правильно интерпретировать разрешенные ходы.

Заключительная позиция (0; 0) – проигрышная. Все позиции, из которых можно прийти к заключительной, являются выигрышными – это все остальные позиции верхнего ряда, все остальные позиции левого столбца и все остальные позиции диагонали, идущей от клетки (0; 0).

Позиции (1; 2) и (2; 1) проигрышные – от них горизонталь, вертикаль и диагональ заполнены только красными клетками. А остальные позиции на тех же горизонталях, вертикалях и диагоналях, что и клетки (1; 2) и (2; 1) – выигрышные, потому что из них можно прийти к этим позициям за один шаг.

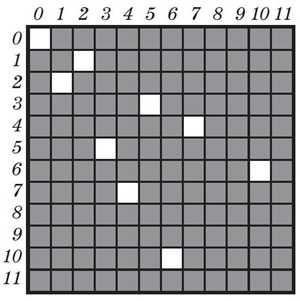
Рассуждая и дальше таким же образом, раскрашиваем всю таблицу. Теперь, когда таблица раскрашена, стало видно, что позиция (9; 6) выигрышная, а позиция (7; 4) – проигрышная.

Задача 167. Задача является продолжением задачи 166. Для ее решения нужно продолжить раскрашивать таблицу. Здесь нам понадобится таблица 11×11 клеток.

Позиция (6; 10) – проигрышная, значит, в игре с этой начальной позицией Второй имеет выигрышную стратегию. Позиция (9; 8) – выигрышная, выигрышной стратегией обладает Первый.

Описать выигрышную стратегию здесь удобно при помощи раскрашенного поля: игрок, имеющий выигрышную стратегию, должен на каждом своем ходе брать столько камешков, чтобы противнику досталась проигрышная позиция – позиция, раскрашенная синим (на нашем рисунке – белым).

Пользуясь раскрашенной таблицей, строим последовательности позиций – с учетом условия, что противник на каждом своем ходу берет по одному камешку из каждой кучи, эти последовательности строятся однозначно:

(6; 10)–(5; 9)–(5; 3)–(4; 2)–(1; 2)–(0; 1)–(0; 0)

(9; 8)–(2; 1)–(1; 0)–(0; 0)

Задача 168. Необязательная. Повторение алгоритмов для Робота с использованием команды цикл пока. Задачу затрудняет то, что направление коридора неизвестно. Придется использовать 4 аналогичные команды для каждого из возможных направлений. Когда нужное направление определится, Робот должен идти в этом направлении, пока коридор не закончится (иначе он будет выполнять программу бесконечно). Поэтому он должен всякий раз проверять, не закончилась ли стена коридора.

Задача 169. Необязательная. В этой задаче учащиеся знакомятся с еще одной математической игрой – Ободок. Собственно, в условии есть подсказка: своим первым ходом Первый должен разделить все точки на две части, так чтобы ход, сделанный в одной части, можно было повторить в другой части. Для этого, прежде всего, в каждой части должно быть точек поровну. Значит, если точек нечетное число, то первым ходом надо провести ободок через 1 точку, если точек четное число – через две. При такой стратегии какой бы ободок ни нарисовал Второй, Первый повторит его в другой части поля. Главное – чтобы поле было четко разделено на 2 части – чтобы нельзя было «залезть» из одной части в другую.

Задача 170. Сложная задача на сообразительность. На первый взгляд, не ясно, с какой стороны подойти к решению. Прежде всего, узнаем, кто будет делать последний ход. В ряду 19 чисел, должно остаться два, значит, последний ход будет делать Первый. Очевидно, здесь нужна равновесная стратегия. И она вполне возможна. Внимательно присмотревшись к ряду чисел, можно найти в нем своего рода «центр», относительно которого можно построить равновесную стратегию. Это число 10. Это число делит числовую линейку на две части. Из чисел левой и правой части можно составить 10  одинаковых сумм (равных 20): 1+19, 2+18, 3+17 и так далее. Каждая из этих сумм делится на 5. Поэтому выигрышная стратегия состоит в том, чтобы на первом ходу зачеркнуть 10, а затем на каждом ходу зачеркивать пару к числу, вычеркнутому Вторым. Тогда в конечном итоге останется какая-нибудь одна пара, сумма которой делится на 5, и выиграет Первый.