Компьютерное дополнение к курсу Информатика 6. 2017

Урок 22. «Выигрышные стратегии»

Теперь ребятам предстоит познакомиться с серией игр, для которых, так же как и для игры Камешки, можно строить выигрышные стратегии путем полного перебора и исследования всех возможных позиций игры. Но теперь позиции будут расположены не на одномерной числовой линейке, а на двумерной  плоскости (в большинстве игр это будет поле 8х8 клеток, хотя, вообще говоря, поле может быть любого (конечного)  размера).

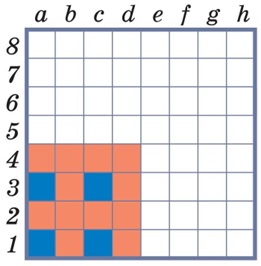
Дальше встает вопрос о том, какие клетки и в каком порядке раскрашивать. Очевидно, нужно искать те позиции, для которых все клетки, куда возможны ходы, уже раскрашены: ведь только такие позиции мы можем оценить как выигрышные или проигрышные. Например, такой будет позиция е1, ведь из нее можно сделать ход только в d1 (выигрышную позицию), значит, е1 – проигрышная позиция. Аналогично, выясняется, что а5 – проигрышная позиция. Теперь уже можно раскрасить клетки е2 и b5, они обе будут выигрышными, так как в результате одного хода из них могут получиться проигрышные позиции (е1 и а5, соответственно). Клетку е3 раскрасим синим – эта позиция проигрышная, так как все ходы из нее ведут в выигрышные позиции (d3, d2 и е2). Двигаясь далее, клетки d5 и е4 раскрасим красным, клетку е5 – синим.

Далее будем раскрашивать следующий «угловой слой» клеток поля, ограничивающий раскрашенные уже клетки сверху и справа, двигаясь слева направо и снизу вверх. Все позиции этого слоя оказываются выигрышными позициями, поскольку для каждой существует ход в проигрышную позицию.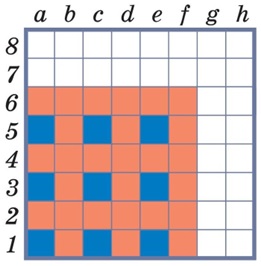

Так ребята раскрашивают клетки поля слоями, двигаясь снизу вверх и слева направо, пока не доходят до верхнего правого угла поля (см. рис. справа). Получаем, что начальная позиция h8 – выигрышная (она раскрашена красным). Значит, в этой игре выигрышная стратегия есть Первого.

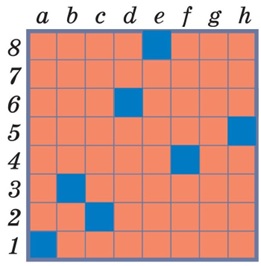
Задача 129. Здесь ребята знакомятся с правилами новой игры Ладья в ходе проведения мини-турнира с соседом по парте. Поля а1 и а2 заданы в качестве начальных не случайно: как дети выяснят, решая следующую задачу, позиция а1 – проигрышная, а позиция а2 – выигрышная.

Задача 130. Как и в задаче 128, наверное, наибольшее число вопросов вызовет порядок раскрашивания полей шахматной доски. Естественно начинать с заключительной позиции – клетки h8 (это проигрышная позиция). Дальше действует знакомый из задачи 128  принцип: сначала раскрасить все позиции, из которых можно попасть в h8 за один ход,  эти позиции будут выигрышными. Таким образом, оказываются помеченными красным все клетки верхнего ряда и крайнего правого столбца. Дальше выбираем позицию, все ходы из которой приводят в раскрашенные клетки, – g7. Она оказывается проигрышной, так как из нее можно попасть только в выигрышные позиции (g8 и h7). После этого мы можем раскрасить все оставшиеся клетки второй строки и второго  столбца справа.

Как видите, раскраска здесь получилась более простой, ее нетрудно описать словами: проигрышными являются только поля главной диагонали доски (диагонали a1–h8), остальные позиции – выигрышные. Значит, если начальная позиция – это одно из полей главной диагонали, то выигрышную стратегию имеет Второй, а в играх с начальной позицией вне главной диагонали – Первый.

Выигрышная стратегия Второго при игре с начальной позицией на главной диагонали заключается в том, чтобы на каждом своем ходу ставить ладью в одну из клеток главной диагонали. Действительно, Первый на первом ходу обязательно уведет ладью с главной диагонали куда-то в сторону, например, по горизонтали. На следующем своем ходу Второй, пройдя столько же клеток по вертикали, сможет поставить ладью обратно на главную диагональ. И так дальше: Первый ладью уводит с диагонали, а Второй возвращает. Если Второй будет играть, следуя этой стратегии, то Первый всякий раз будет оказываться вне диагонали, а значит, не сможет попасть на поле h8 и выиграть.

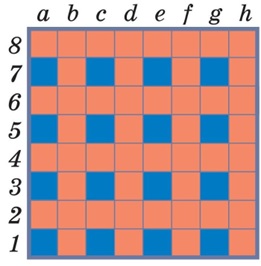
Аналогично строится и выигрышная стратегия Первого в играх с начальной позицией вне главной диагонали: первым своим ходом Первый должен поставить ладью на главную диагональ – он это всегда сможет сделать, т. к. начальная позиция – это поле вне диагонали. Дальше Второй на каждом своем ходу будет ладью уводить с диагонали (просто не сможет пойти иначе), а Первый, следуя стратегии, – возвращать.

Задача 131. Здесь раскраска полей шахматной доски будет довольно затейливой. Начать, как обычно, надо с заключительной позиции – а1 (это проигрышная позиция), затем надо пометить клетки, из которых можно попасть в а1 за один ход (выигрышные позиции), – это все оставшиеся клетки крайнего левого столбца, нижней строки и диагонального ряда а1–h8.  Далее помечаем клетки, из которых можно сделать ходы только в раскрашенные позиции: b3 и с2. Они оказываются проигрышными. И так далее. Интересно, что в результате на поле оказывается всего 7 проигрышных позиций: а1, b3, с2, d6, е8, f4, h5.

Таким образом, заданные позиции: g8 – выигрышная, а h5 – проигрышная. Описать выигрышную стратегию здесь можно, только ссылаясь на раскрашенную шахматную доску: стратегия, как и обычно, состоит в том, чтобы оставлять противнику проигрышную позицию – одну из позиций b3, с2, d6, е8, f4, h5. Собственно, этот список из шести полей – это и есть тот список, который требуется выписать в последней части задания: шесть полей, с начальными позициями в которых в игре Ферзь выигрышная стратегия есть у Второго. А список полей с выигрышной стратегией для Первого – это любые 6 полей, раскрашенных красным, вариантов здесь много.

Задача 132. Данная задача аналогична задаче 124, на ее решение уйдет много времени, поэтому мы советуем оставить эту задачу на дом. Построить дерево – дело несложное, хотя и длительное: необходимо вырезать заготовки полей и нарисовать все позиции, ничего не забыв и не перепутав. Посоветуйте детям не приклеивать сразу накрепко позиции на места, а сначала только наметить – мазнуть (или капнуть) немного клея в серединку. 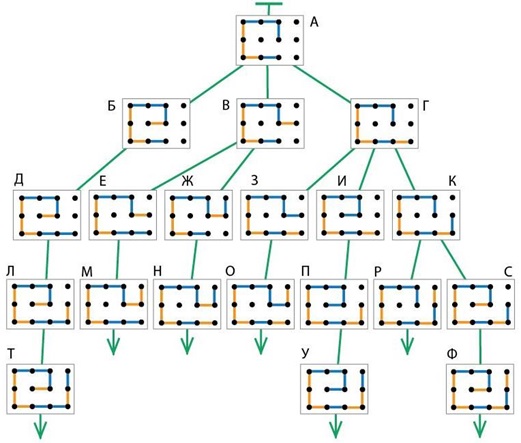Потом, когда все будет проверено еще раз, можно добавить клея под уголки полей. Пример части дерева игры Ползунок, которую требуется построить в задаче, приведен на рисунке на следующей странице. Очередь ходить из заданной позиции – у Второго, он рисует оранжевым карандашом.

Исследование позиций, как обычно, начинаем с конца, с заключительных позиций. Помечаем синим все листы дерева (позиции Т, М, Н, О, У, Р и Ф) – заключительные позиции всегда проигрышные. Позиции, предыдущие перед листьями, помечаем красным (это позиции Л, Е, Ж, З, П, К, С) – они выигрышные. Позиции Д, В, И – проигрышные, так как все следующие после них позиции – выигрышные. Оставшиеся позиции Б, А, Г – выигрышные, так как после них есть следующие проигрышные позиции.

Итак, позиция А – выигрышная, значит, тот игрок, чья очередь ходить из этой позиции, имеет выигрышную стратегию – это Второй. Выигрышная стратегия состоит в том, что Второй должен сначала сделать ход, приводящий к позиции В. Дальше можно по дереву проследить, что какой бы ход ни сделал Первый, Второй на следующем ходу выиграет. Таким образом, возможны две последовательности позиций в партиях, где Второй следует выигрышной стратегии: А–В–Е–М  и  А–В–Ж–Н.

Задача 133. Детям, которые решили все предыдущие задачи урока, эта задача покажется несложной. Сложным будет, быть может, только переход от шахматной доски к обычной таблице и неграфическое представление правил игры. Тем, у кого возникнут затруднения, предложите еще раз перечитать материал листа определений. Начальная позиция (4; 5) – выигрышная, значит, Первый имеет выигрышную стратегию. Требуемая последовательность позиций выглядит так:

(4; 5)–(4; 4)–(3; 3)–(2; 2)–(1; 2)–(0; 2)–(0; 1)–(0; 0)

Задача 134. Довольно сложная задача на сообразительность. Некоторые утверждения могут поставить ученика в тупик. Посоветуйте таким детям начать с самого простого. Все элементы множества – двузначные нечетные числа. Этих чисел много, но второе утверждение ограничивает выбор. Попробуем выписать все числа, которые нас устраивают. Начинаем перебор с первой цифры, вторую находим вычитанием из 10 (четные числа не записываем). Итак, нам подходит такое множество А из пяти чисел: {19, 37, 55, 73, 91}.

Теперь переходим к третьему утверждению: «Самое большое число больше суммы всех остальных на 1». В множестве А нет двух чисел, различающихся на 1, значит, нам нужно искать подмножества А из 3 и более чисел. Все множество А третьему условию не удовлетворяет. И любое подмножество А из 4 чисел тоже – масса любых трех чисел из него будет трехзначным числом. Значит, мы должны рассматривать только подмножества из трех чисел. Для поиска можно построить дерево всех таких подмножеств. Впрочем, достаточно построить дерево всех возможных пар чисел из множества А и для каждой пары найти сумму этих чисел, сравнить ее с числами множества А. Но можно действовать и методом проб и ошибок: складывать разные пары чисел из множества А и смотреть, получается ли сумма, на 1 больше третьего числа из множества.

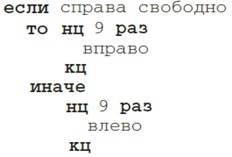
Вот три подходящих подмножества А: {19, 37, 55}, {19, 55, 73} и {37, 55, 91}. Для ответа годятся любые два из них.

Задача 135. Составление алгоритма для Робота. Поскольку мы не знаем, в каком углу поля стоит Робот, придется использовать условные конструкции. Итак, схема алгоритма будет такой. Сначала продвигаем Робота на противоположный конец поля по вертикали. Робот ведь стоит в одном из углов, поэтому одно из двух: либо вверху свободно, либо вверху стена:

Теперь двигаем Робота на противоположный край поля по горизонтали, аналогично:

Здесь важно помнить, что если в ряду 10 клеток, то Робот должен сделать 9 шагов вправо или влево, и если в столбце 14 клеток, то Робот должен сделать 13 шагов вверх или вниз.

Задача 136. Повторение алгоритмов для Робота. Здесь, находясь в начальной позиции, Робот не может выяснить, в какую сторону ему надо идти. Вариантов два – направо 10 шагов или налево 10 шагов. Будем действовать по такой схеме. Сделаем 10 шагов вправо. Затем, если справа свободно, делаем еще шаг вправо – мы нашли выход из коридора. В противном случае делаем 21 шаг влево. Робот выведен из коридора.

Задача 137. Необязательная.  Эта задача – пример «жизненной» ситуации, когда может пригодиться умение найти выигрышную стратегию в игре. Внимательно прочитав условие задачи, дети догадаются, что ситуация похожа на игру в Камешки с начальной позицией 9 камешков и разрешенными ходами в 1, 2 и 3 камешка. А значит, и решать эту задачу нужно ровно так же, как задачи на поиск выигрышной стратегии в этой игре.

Для решения задачи мы можем использовать числовую линейку из предыдущей задачи, только отбросив (мысленно) последнюю клетку – 10:

Позиция 9 – выигрышная, так что у Алеши есть все шансы «обрести славу победителя змея», ибо выигрышная стратегия будет у того богатыря, кто начнет бой Первым. А стратегия здесь совершенно такая же, как и в предыдущей задаче: на первом ходу оставить 8 голов, на втором – 4 головы, на третьем – отрубить все оставшиеся. Как видим, эта задача решается в точности так же, как и предыдущая.

Задача 138. Необязательная. На листе определений «Выигрышные и проигрышные позиции» был дан анализ позиций игры Камешки, хотя и с несколько иными правилами. Однако если ученик затрудняется с решением, вполне логично отослать его к этому листу определений. Итак, позиция 0 – проигрышная, раскрашиваем ее синим. Позиции 1, 2 и 3 – выигрышные: игрок забирает все камешки и выигрывает. Позиция 4 – проигрышная: любой ход из нее оставляет противнику выигрышную позицию. Позиция 5 – выигрышная: взяв 1 камешек, игрок оставляет противнику проигрышную позицию 4. Позиция 6 – выигрышная: взяв 2 камешка, игрок оставляет противнику снова позицию 4. Позиция 7 – выигрышная: взяв 3 камешка, игрок оставляет противнику все ту же позицию 4. Позиция 8 – проигрышная: любой ход из нее ведет в выигрышную позицию. Позиции 9 и 10 – выигрышные. Таким образом, у нас получилась такая числовая линейка:

Как видим, выигрышная стратегия имеется у Первого (конечно, если мы не допускаем, что он, вопреки своей выигрышной стратегии, возьмет на первом ходу 1 камешек, в этом случае выигрышная стратегия будет у Второго, но, еще раз повторим, такой случай мы не рассматриваем). Итак, выигрышная стратегия очень проста: Первый должен после первого хода оставить 8 камешков, после второго – 4 камешка, на третьем – забрать все оставшиеся.

Партия, в которой Первый следует выигрышной стратегии, а Второй на каждом ходу забирает по 2 камешка, будет выглядеть так:

10 – 8 – 6 – 4 – 2 – 0

Задача 139. Необязательная. Игра Назови 26 на самом деле очень похожа на игру Сотня. Но понять это сразу детям будет не так-то просто, да, впрочем, это и не обязательно. В тетради проектов (с. 33) есть полная числовая линейка для решения этой задачи: от 26 до 0 в порядке убывания. Раскрасив всю эту линейку, детям будет уже не трудно сформулировать выигрышную стратегию. Проигрышные позиции в этой игре – это числа 26, 21, 16, 11, 6 и 1. Позиция 0 выигрышная, значит Первый имеет выигрышную стратегию: на первом ходу он должен назвать число 1, а дальше добавлять каждый раз столько, чтобы в сумме получалось одно из чисел: 6, 11, 16, 21 или 26.

Задача 140. Необязательная. Построение прямоугольных треугольников по заданной площади. Задача имеет не единственное решение. Возможные варианты – треугольники с катетами 1 и 24, 2 и 12, 3 и 8, 4 и 6 ед.кв.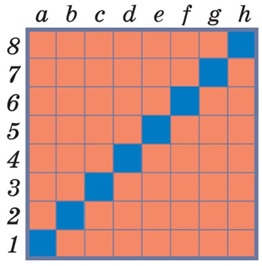