Компьютерное дополнение к курсу Информатика 6. 2017

Уроки 19–20. «Команды-запросы Робота. Условие»

На этом листе определений мы вводим новую конструкцию нашего учебного алгоритмического языка. Это условная команда если… то… иначе. Это принципиально новая для ребят конструкция. До настоящего момента все наши алгоритмы содержали заранее определенные команды, не зависящие ни от каких условий. Часто, однако, и в программировании, и в жизни действия исполнителя зависят от тех или иных условий. Например, мы просим ребенка сходить в булочную и даем ему такую инструкцию: «Если будут булочки с маком, купи 2 штуки, если булочек с маком не будет, купи 1 плюшку, если и плюшек не будет, купи 2 сдобные булки, а если и их не будет, купи просто батон белого хлеба». В программировании условные команды (ветвления), так же как и в жизни, чрезвычайно распространены. В случае с нашим исполнителем Роботом вполне можно представить себе ситуации, в которых уместны были бы условные команды. Учитывая, что на поле могут быть стены, а также закрашенные клетки. Например, мы могли бы скомандовать Роботу: «Если справа свободно, сделай шаг вправо». Или: «Если клетка чистая, закрась ее». И так далее. Но для этого мы должны научить Робота отвечать на вопросы типа: «Справа свободно?» Или: «Клетка закрашена?» Подобные выражения мы будем называть командами-запросами. Всего в нашем алгоритмическом языке 12 таких команд:

Последние две (температура и радиация) для нас пока не актуальны. Обратите внимание, что в отличие от вопросов в русском языке наши команды-запросы не сопровождаются вопросительным знаком. И если в русском языке ответом на подобные вопросы будет слово «да» или «нет», то Робот в ответ выдает значение «истина» или «ложь». Думаем, ребятам не придется объяснять, что означают эти слова.

Итак, у нас есть команды-запросы, с помощью которых мы будем записывать условие в условной конструкции, которая имеет следующий формат:

Как будет обрабатываться такой запрос? Сначала Робот проверяет условие. Если условие истинно, то Робот выполняет одну за другой команды из последовательности 1. Если условие ложно, то последовательность 1 пропускается и выполняются команды из последовательности 2. Служебное слово все отмечает конец условной конструкции.

Иногда и в жизни, и в программировании мы ограничиваемся в своих «условиях» командой если, например: «Если будут булочки с корицей, купи две штуки». В данном случае мы не определяем для исполнителя, что ему делать, в случае если булочек с корицей не будет. На самом деле это означает не делать ничего.  Именно так и будет интерпретироваться неполная условная конструкция:

То есть если условие оказывается ложным, то Робот не выполняет команды из последовательности 1, а сразу переходит к команде, следующей за словом все.

На листе определений приводится несколько содержательных примеров использования условной конструкции в алгоритмах для Робота. На самом деле эта новая конструкция совершенно несложная, т.к. имеет прозрачные аналогии в русском языке.

Задача 102. Простая задача на закрепление нового материала. Здесь ребенку предлагается поработать Роботом, определив значение команд-запросов для каждой из отмеченных клеток поля. Напомните детям, что согласно нашим договоренностям, по границе поля Робота идут стены.

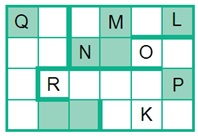
Задача 103. Задача, обратная предыдущей. По результатам команд-вопросов необходимо определить положение клетки поля. Заметим, что для некоторых наборов значений положение клетки неоднозначно, например клеток О и К. Работа требует внимательности и сосредоточенности.

Вот один из вариантов ответа:

Задача 104. Необязательная. Поиск трех одинаковых фигурок. В данном случае задача сложная, так как алфавит незнакомый, букв много и они очень похожи друг на друга. Метод решения – полный перебор. Желательно для надежности придерживаться той или иной системы просмотра и обязательно делать пометки. 

Три одинаковые буквы: 

Задача 105. Проверка усвоения нового материала.

Задача 106. Заметим, что если исходить из того, что каждый из игроков стремится выиграть и не дать выиграть противнику, то такая партия, скорее всего, окончится ничьей. Поэтому учащимся придется «заставить» Второго играть нерационально.

Задача 107. Необязательная. Начнем раскладывать монеты по кошелькам. Ясно, что в одном из кошельков должен лежать 1 рубль, иначе мы его никак не сможем выдать. Чтобы выдать 2 р. мы можем положить в другой кошелек 1 р. или 2 р. Но ведь кошельков у нас всего семь, а монет 127, значит, лучше класть в кошелек бо́льшую сумму. Итак, теперь у нас в первом кошельке 1 р., во втором – 2 р. Чтобы выдать сумму в 3 р., мы просто отдадим два этих кошелька, а вот 4 р. Мы никак пока не получим. Значит, в третий кошелек нужно положить 4 р. С помощью этих трех кошельков мы теперь сможем выдать: 1 р., 2 р., 3 р., 4 р., 5 р. (1+4), 6 р. (2+4), 7 р. (1+2+4). Восемь рублей мы никак не получим, значит, в четвертый кошелек нужно положить 8 р. Продолжая аналогичные рассуждения, получаем, что остальные суммы также равны степеням числа 2.

Ответ: в кошельки нужно положить следующие суммы: 1 р., 2 р., 4 р., 8 р., 16 р., 32 р., 64 р.

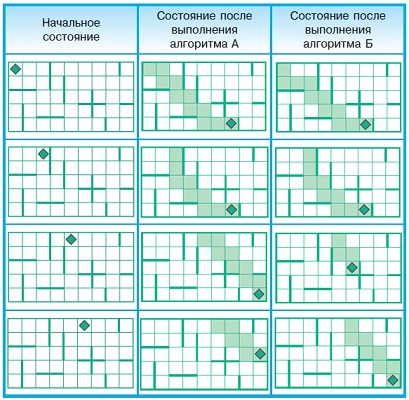
Задача 108. Не слишком сложная, но объемная и очень важная задача на понимание принципа работы условной конструкции. Рассмотрим, например, как будет выполняться алгоритм А на поле 2. 1-й цикл: справа стена, значит, команда вправо пропускается, выполняется команда вниз. 2-й цикл – как первый. 3-й цикл: выполняются вправо и вниз. 4-й цикл – как третий. 5-й цикл: выполняется команда вправо, команда вниз пропускается. 6-й цикл – как пятый. Важно, чтобы дети это понимали и не прекращали алгоритм раньше, чем нужно.

Ответ:

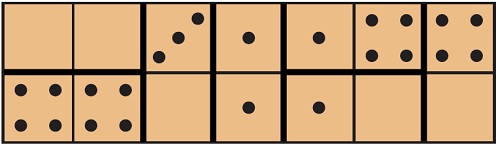
Задача 109. Необязательная. Задача средней сложности на сообразительность. Здесь главная загвоздка в том, чтобы костяшки не повторялись. Идем справа налево: 4–0. Дальше, чтобы не дублировать эту костяшку, режем горизонтально: 4–1,0–1. Дальше, чтобы не повторяться, режем вертикально: 1–1, 3–0. Наконец, чтобы не повторяться, режем горизонтально: 4–4, 0–0.

Ответ:

Задача 110. Составление алгоритма с условной конструкцией. Разумеется, задачу можно решать по-разному и в ответе алгоритмы, скорее всего, у ребят будут разными. Достоинством условной конструкции является то, что даже если в процессе ее выполнения на пути у Робота встала стена, отказа не будет – команды просто будут проигнорированы.

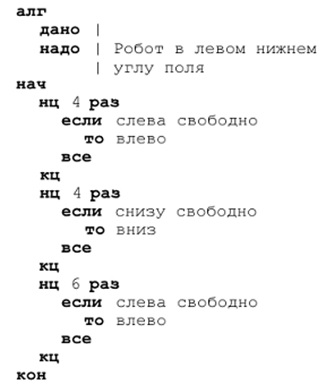
Поэтому для всех четырех вариантов начального состояния Робот может сначала, при условии, что слева свободно, идти 4 раза влево (если может, то пройдет, если нет, то останется в прежнем положении или остановится, упершись в стенку). Дальше, если внизу свободно, на 4 клетки вниз. И, наконец, если слева свободно, на 6 клеток влево.

Ответ:

Задача 111. Закрепляем составление алгоритма с условной конструкцией. Затрудняет решение задачи то, что нужно действовать умозрительно, на рисунок можно опереться только как на возможный вариант поля. Итак, алгоритм а): повторяем 10 раз: шагаем вправо, если клетка закрашена, смещаемся вниз на 1 клетку, закрашиваем ее, поднимаемся вверх. Алгоритм б): повторяем 10 раз: шагаем вправо, если клетка закрашена, смещаемся вниз на 1 клетку, закрашиваем ее, смещаемся вверх на 2 клетки, закрашиваем клетку, смещаемся вниз на 1 клетку.  Алгоритм в) удобнее выполнять справа налево, поэтому сначала перемещаем Робота на 10 клеток вправо (последняя закрашенная клетка находится не далее чем в 10 шагах от Робота). Далее: повторяем 10 раз: если клетка закрашена, смещаемся влево на 1 клетку и закрашиваем ее, смещаемся влево на 1 шаг. Алгоритм г): повторяем 10 раз: смещаемся вправо на 1 шаг, если клетка закрашена, смещаемся вправо и закрашиваем. Ответ:

а) 

б)

в)

г)

Задача 112. Игра Ползунок интересна тем, что в ней место числовой интуиции занимает геометрическая. При этом геометрия здесь не обычная, которую учат в школе, а более современная – это, можно сказать, дискретная топология (дискретная потому, что в ней действие разворачивается в пространстве конечного числа точек, а топология потому, что для нас несущественно расстояние между этими точками, а существенно только их взаимное расположение).

Ответы на вопросы позволят понять, насколько ученик разобрался с правилами игры. Если кому-то это оказалось не под силу, попросите его сыграть несколько партий в Ползунок с соседом – в процессе игры многое станет ясным.

 Ответ: В партии с последовательностью S было сделано 9 ходов, Первый сделал 5 ходов, а Второй – 4; выиграл Первый.

Задача 113. Здесь от учащихся требуется лишь понимание правил игры в Ползунок. Напомните ребятам, что нужно каждый новый отрезок  проводить красным или синим карандашом – в зависимости от того, кто делает ход. Необходимые поля ребята найдут на вкладыше тетради проектов.

Очень важно, чтобы решение задачи закончилось проверкой. Главное условие – чтобы последняя позиция в последовательности  действительно была заключительной. Для этого на поле должна получиться ломаная, которую уже нельзя продолжить. Также нужно проверить, что при переходе от каждой позиции к следующей добавлялся ровно один отрезок. Наконец, стоит просмотреть всю последовательность, проверяя, соответствует ли очередность ходов цвету появившегося отрезка и соответствует ли следующая позиция предыдущей (все отрезки каждой позиции должны повторяться и на следующих позициях).

Задача 114. Повторение перебора вариантов. Прежде всего, переведем все ложные утверждения в истинные, чтобы лучше понимать все условия, касающиеся нашего будущего дерева. Итак:

·         Всякий элемент нашего дерева – круглая бусина черного или белого цвета.

·         В нашем дереве 8 или более листьев и все они располагаются на 3-ем уровне.

·         В нашем дереве нет двух одинаковых последовательностей.

Итак, мы с вами понимаем, что из двухэлементного множества мы можем построить не более 8 разных трехэлементных последовательностей, то есть в нашем дереве должны быть 2 элемента первого уровня, причем разные! Дети, конечно, этого пока не понимают и, уж конечно, не могут обосновать. Но, возможно, кто-то из них вспомнит, как строил дерево перебора всех вариантов цепочек из множества {0,1}. Тогда на 3-м уровне как раз получилось 8 элементов. Но это не важно. Пусть ребята действуют методом проб и ошибок. Очень скоро они поймут, что с одним элементом первого уровня разных последовательностей будет маловато. Если ребенок совсем запутался, попросите его построить дерево перебора всех вариантов из нуля и единицы. Дальше уже, скорее всего, сообразит сам.

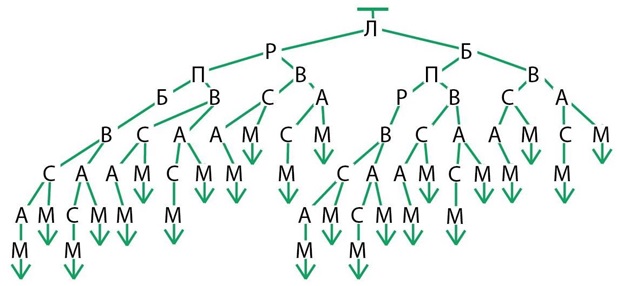
Задача 115. Необязательная. Больше всего данная задача напоминает задачу 59, только здесь не нужно искать кратчайший маршрут. В принципе, здесь даже не требуется выписывать все возможные маршруты, а лишь указать их число. Однако перебрать все способы перемещения из города Л в город М в голове, без всякой графической опоры, никому из детей, скорее всего, не удастся. Как видите, в отличие от задачи 59, маршрутов здесь получается довольно много, поэтому необходимо построить дерево перебора.

Но и построить дерево перебора здесь не так-то просто, поэтому данная

задача предназначается, в основном, сильным и техничным детям. Итак, из города Л можно попасть в города Р и Б, значит, на первом уровне у нас будет элемент Л, а на втором – два элемента: Р и Б. Из каждой из них пойдут две большие ветки. Самые сообразительные дети, возможно, заметят, что элементы Б и Р относительно элемента Л и остальных ребер графа расположены аналогично (симметрично), поэтому ветки из Р и из Б будут одинаковы с точностью до перестановки букв. В частности, в ветке из Б будет столько же последовательностей, что и из Р. Поэтому в сущности  можно рисовать в дереве перебора лишь одну ветку, а потом просто посчитать, сколько последовательностей будет в другой ветке и сколько последовательностей будет всего. Если ребенок не догадается до симметричного строения дерева, то подсказывать ему, конечно, не надо, пусть строит обе ветки (возможно, догадка озарит его на середине пути).

Ответ: из города Л в город М можно попасть 24 способами. (См. рис.)