Компьютерное дополнение к курсу Информатика 6. 2017

Урок 18. «Игры с полной информацией. Дерево игры»

Как видно из текста на листе определений, наше понятие игры охватывает далеко не все игры, в которые играют люди. Нас будут интересовать только игры двух игроков с полной информацией – игры, для которых характерны следующие особенности:

– в любой момент игры каждому из игроков полностью известно все, что произошло в игре до этого момента и какие ходы возможны;

– каждая позиция игры зависит только от начальной позиции и ходов игроков;

– количество возможных ходов ограничено, что гарантирует окончание игры в некоторый момент.

Игры с полной информацией являются предметом изучения нескольких разделов математики, в частности дискретной математики, теоретической информатики и топологии (в топологии подобные игры называют топологическими).

На первый взгляд может показаться, что изучение таких простых игр – дело несерьезное, потребное, скорее, для развлечения и досуга. На самом деле игра, даже с совсем простыми правилами, часто оказывается удобной моделью для исследования различных процессов, происходящих в природе (на макро- или микроуровне) и обществе (экономические и социальные процессы). Результаты, полученные математиками при изучении игр с полной информацией, позволили им перейти к изучению игр с неполной информацией – игр, в которых присутствует элемент случайности, например карточных игр. Полученные результаты нашли применение в самых разных областях знаний – при изучении процесса размножения бактерий или  развитии теории проведения переговоров в бизнесе, изучении возможных исходов ядерной войны, различных процессов экономики и даже в практической психологии, в применении к обычным разводам.

При изучении игр с полной информацией обычно рассматриваются только такие партии, которые заканчиваются за конечное число ходов. И на листе определений мы обошли вниманием случай, когда игра продолжается до бесконечности. Бесконечная партия возможна и в реальных играх, например в шахматах. Там даже приняты специальные меры против такой ситуации: партия в шахматы считается закончившейся вничью, если позиция повторилась троекратно. Такие же договоренности (о трехкратном повторении) вводят и математики, когда хотят избежать рассмотрения игр, продолжающихся бесконечно.

Наиболее сложным из новых понятий, введенных на листе определений, является позиция игры, ведь понятия правил игры, хода, победителя и т. п. ребятам, скорее всего, уже знакомы. Понятие позиции игры очень емкое. Позиция игры – это поле и все ходы, сделанные обоими игроками к данному моменту. Каждый ход игрока – это разрешенное правилами игры изменение позиции игры. Правила игры оговаривают все возможные начальные позиции игры, а также все возможные заключительные позиции – такие позиции, по достижении которых игра заканчивается.

C введением понятия «позиция игры» у нас появляется также возможность ввести понятия последовательности позиций игры и дерева игры. Построение дерева всегда помогает нам, когда необходимо осуществить перебор всех возможных партий игры с данными правилами.  Удержать все возникающие в ходе игры ветвления в голове подчас оказывается затруднительно даже взрослому, а ребенку и подавно. Дерево же дает простую и понятную модель, отражающую сразу все варианты возможного развития игры от первого до последнего шага, от начальной до любой заключительной позиции. Итак, последовательность позиций – это способ представить динамический процесс в виде статичной последовательности моментальных снимков. Дерево игры – это способ фиксировать различные варианты развития событий.

Умение представлять себе, а иногда и рисовать дерево возможностей и вариантов совместной деятельности, сотрудничества или конфликта может пригодиться детям и в дальнейшей жизни.

Для детей, которые работали в 4 классе с нашим курсом информатики, тема этого урока будет повторением и обобщением пройденного. При работе  с таким классом мы предлагаем вам воспользоваться альтернативным планированием – потратить меньше учебных часов на этот материал, обобщив основные понятия, и перейти к следующим темам, а также к решению дополнительных и трудных задач.

Задача 93. Пока что дети только накапливают опыт в игре Камешки и не знакомы с понятием выигрышной стратегии, поэтому придумать, в буквальном смысле, партию игры с условием выигрыша Первого или Второго многим будет нелегко. Для таких детей всегда есть запасной вариант – построить дерево игры с данными правилами. По дереву будет совсем просто найти нужные цепочки позиций и выписать соответствующие им партии в тетрадь.  Поскольку по условию дерево строить не требуется, можно сделать это на черновике. Главное – увидеть на этом рисунке подходящую последовательность позиций. И, конечно, не нужно строить дерево целиком – как только будут определены нужные партии, можно остановиться.

Задача 94. Сыграть 8 партий в Камешки, конечно, несложно, но необходимо еще правильно записать результаты в таблицу и проследить за очередностью ходов. Указание, касающееся очередности ходов, мы приводим для того, чтобы игроки были в равном положении. В данной игре Первый всегда имеет возможность выиграть (имеет выигрышную стратегию), однако говорить об этом пока рано – дети должны освоиться с правилами игры. Сильные дети, стараясь выиграть, сами интуитивно выработают какую-то собственную стратегию, которая поможет им в этом.

Заполнять таблицу, как и во всех задачах на проведение турниров в малых группах, лучше всего по ходу игры, т. е. заносить в нее результаты по окончании каждой партии. В пустых клетках заголовка таблицы нужно написать имена или фамилии игроков, но не номера, иначе дети будут путать их с Первым и Вторым. Чтобы ребятам было легче отвечать потом на вопрос, можно цветом помечать в таблице очки, заработанные Первым в каждой партии. Или можно поставить пометку в углу клетки игрока, который играл Первым. После того как будут сыграны все 8 партий, учащиеся суммируют очки в каждом столбце. Заканчивается решение задачи ответом на вопрос. Проследите за тем, чтобы по окончании решения задачи у каждого из  пары игроков была заполнена своя таблица, а не одна на двоих.

Возможно, кто-то из сильных учащихся в ходе игр обратит внимание на то, что Первый выигрывает чаще Второго. Такому ученику можно дать задание подумать, почему так получается и как именно должен играть Первый, чтобы выиграть наверняка (как бы ни играл Второй).

Задача 95. Очень важно, чтобы с этой задачей справились все ребята. При построении дерева Б ребятам придется решать две задачи – представить себе дерево (спроектировать его в уме) и разместить, нарисовать это дерево в тетради. Делать это одновременно могут далеко не все, поэтому в данной задаче (первой подобной задаче после листа определений) мы советуем сначала нарисовать дерево на черновике, где можно зачеркивать и стирать, или хотя бы  работать в тетради карандашом. Если вы видите, что кто-то из учеников не знает, с чего начать, можно помочь ему следующими вопросами: «Какие ходы может сделать Первый из начальной позиции?», «Какие позиции при этом могут получиться?», «Какие ходы может сделать Второй из возможных позиций второго уровня?», «Какие позиции могут при этом получиться?» и т. п. Если учащийся не может ответить на эти вопросы, стоит еще раз вместе разобраться, как построено дерево А на листе определений.

Чтобы при построении дерева не запутаться, перебирая возможные позиции, лучше располагать все бусины, следующие за некоторой бусиной, в определенном порядке, например слева направо по убыванию числа камешков в позициях. Деревья, нарисованные учащимися, могут различаться. Мы приводим дерево, в котором бусины упорядочены так, как мы говорили: в порядке убывания числа камешков в позициях слева направо.

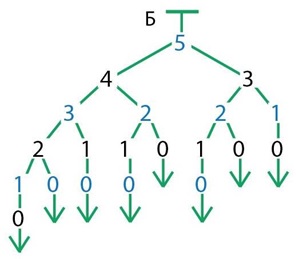
Возможно, у вас в классе найдутся наблюдательные дети, которые заметят, что дерево Б – это «ветка» из дерева А с листа определений, начинающаяся с позиции 5 второго уровня, и будут срисовывать его. Это не страшно, но лучше, если такие дети оставят свое открытие при себе.

Второе задание мы предлагаем ребятам для того, чтобы они сопоставили дерево игры и процесс проведения реальных партий. Как говорилось на листе определений, дерево игры содержит все возможные партии, проводимые по данным правилам. По дереву можно получить информацию о том, кто выиграл в той или иной партии и на каком ходу. В дереве все ходы, которые получились в результате хода Первого, записаны синим, поэтому синим ребята должны обвести все нули, написанные синим, а зеленым – все другие нули.

Задача 96. Прежде всего заметим, что если в дано мы потребуем, чтобы поле имело размер 11х11 клеток, то у нас будет большая свобода при построении конструкций повторения, т.к. нас не будет волновать, если Робот выйдет на 11-ю клетку поля. В результате алгоритм приобретет более простую и ясную структуру. И еще одно замечание: разумеется, решением задачи могут быть разные алгоритмы. Ниже мы приводим один из вариантов:

Задача 97. Необязательная. Прежде чем строить пересечение и объединение множеств, конечно, нужно нарисовать сами исходные множества S и R. При этом важно не забыть, что в множестве не может быть повторяющихся элементов. Множество всех букв, которые встречаются в слове КАРТОШКА, это множество S = {К, А, Р, Т, О, Ш}. Множество всех букв, которые встречаются в слове МАКАРОНЫ, это множество R = {М, А, К, Р, О, Н, Ы}.

Ответ: пересечение множеств S и R: {А, К, Р, О}, объединение множеств S и R: {К, А, Р, Т, О, Ш, М, Н, Ы}.

Задача 98. В этой задаче добавлено ограничение на длину партии (и, соответственно, на длину последовательности позиций). Последующее построение дерева и работа с ним являются не только развитием основной темы, но и одновременно повторением темы «Последовательность из дерева». Вариантов построения последовательностей А и Б есть несколько. Обратите внимание, что при построении этих последовательностей необязательно рассматривать только такие партии, в которых оба игрока стремятся победить, – в этих партиях соперники могут делать любые допустимые ходы, даже «глупые», и поддаваться противнику. Например, в качестве последовательности А можно построить и такие:

5–4–2–0 или 5–3–2–0

При этом в партии, соответствующей левой последовательности, Второй ведет себя крайне неблагоразумно – берет 2 камешка и на следующем ходу проигрывает, хотя мог бы сразу забрать все 4 камешка и тут же выиграть! Тем не менее последовательность эта построена по правилам игры и поэтому является решением. В партии, соответствующей правой последовательности, первый ход  Первого определяет его победу – Второму просто некуда деваться, он делает единственный возможный ход – берет 2 камешка. Это можно обсудить с сильными детьми (а также со всеми детьми, которые работали с курсом 4 класса). Хорошим продолжением этого обсуждения станет работа с возможными вариантами последовательности Б: для того чтобы Второй выиграл на четвёртом ходу, Первый на первом ходу не должен брать ни 2, ни 4 камешка (иначе игра сама собой закончится раньше четвертого хода).

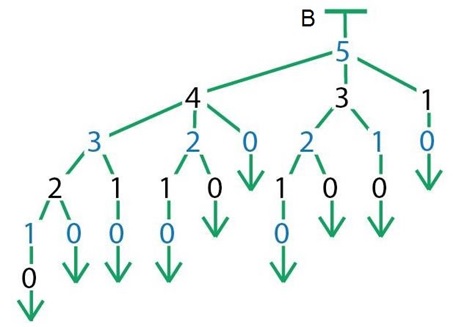
И дальше игроки должны все время делать «неблагоразумные» ходы, всеми силами стремясь затянуть игру. После того как будет построено дерево В, сильных и средних учеников можно попросить, пользуясь деревом, построить все возможные варианты для последовательностей А и Б.       

Ответ: в дереве В красным можно обвести один из двух листьев на третьем уровне, а синим – один из трёх на четвертом уровне.

Задача 99. Эта задача будет новой для всех учащихся – и для тех, кто изучает информатику не первый год, и для «новеньких» – задач на формализацию правил игры в курсе 5 класса не было. Если предыдущие задачи по теме, скорее, знакомили детей с практической стороной вопроса, то эта задача проверяет усвоение теоретического материала об играх с полной информацией.

Игра Крестики-нолики, наверняка, знакома всем учащимся, поэтому понять общее описание правил этой игры детям, скорее всего, будет нетрудно. Трудная часть – формализация данного неформального описания. Но мы надеемся, что образец поможет детям при решении. Конечно, не у всех детей получится сразу правильно и гладко сформулировать формальные правила игры. Думаем, здесь не стоит слишком придираться к речевым ошибкам и стилю изложения. Достаточно, если ребенок напишет более-менее понятный текст, который будет следовать приведенному образцу и на самом деле будет описывать правила игры в Крестики-нолики.

Проследите, чтобы дети при рисовании примеров изобразили действительно возможные позиции игры, а не просто ряды крестиков или ноликов на поле. Позиция, на которой нарисованы только три крестика и ни одного нолика, в этой игре невозможна!

Ответ:

Начальная позиция. Поле размером 3х3 клетки.

Возможные ходы. Во время хода игрок рисует свой значок в свободной клетке поля. Первый игрок рисует крестики, Второй игрок рисует нолики.

Как определить победителя. В этой игре заключительные позиции бывают трех видов:

1) на поле возник ряд из трёх крестиков (по горизонтали, по вертикали или по диагонали) – выиграл Первый;

2) на поле возник ряд из трех ноликов (по горизонтали, по вертикали или по диагонали) – выиграл Второй;

3) все клетки поля заполнены значками, но ряда из трёх одинаковых значков не возникло – игра закончилась вничью.

Задача 100. В предыдущей задаче об игре Крестики-нолики (задаче 99) дети только формализовали правила игры. Теперь им предлагается разобраться с  последовательностью позиций одной партии этой игры. Так как игра эта детям знакома и последовательности позиций (правда, других игр) они тоже видели, мы надеемся, что эта задача будет нетрудной для большинства детей. Ее можно оставить на дом.

Задача 101. Необязательная. Мы уже говорили, что необязательные задачи в нашем учебнике встречаются самые разные. Тем не менее их можно условно разделить на несколько групп: задачи на повторение, практические задачи, математические задачи и т.д.  Как видите, эта задача открывает новую серию необязательных задач – лингвистические задачи. Лингвистические задачи имеют ряд отличий от других задач, особенно от информатических и математических задач. В задачах нашего курса мы все время старались, чтобы все правила игры были выписаны явно. Например, чтобы говорить о буквах русского языка, следует их все выписать, чтобы говорить о гласных буквах, их опять-таки надо выписать явно. В лингвистических же задачах часто используются сведения, явно не введенные, но которые могут быть почерпнуты из других источников или представляются очень правдоподобными. Эта разница весьма принципиальна и отличает математику от других наук, обращающихся, как и лингвистика, за информацией к внешнему миру, а не только к правилам математической игры. Математическая информатика работает с абстрактными моделями реальных компьютеров, которые работают по ясным и явно заданным правилам и, в частности, не могут допустить сбой. В отличие от таких абстрактных моделей обычная вычислительная машина может дать сбой по разным причинам, например из-за колебания напряжения в электрической сети или из-за того, что авторы операционной системы этой машины написали программу так, что она работает не в точности как задумано, а зависает в ходе вполне законной деятельности пользователя.

Почти все лингвистические задачи предназначены, в основном, для сильных и сообразительных детей, которые любят рассуждать. Для решения таких задач кроме обычной (формальной, математической) логики нужна некоторая языковая интуиция. На решение таких задач трудно навести и уж тем более разложить его «по полочкам». Поэтому если ребенок в такой задаче совсем запутался и не сдвигается с мертвой точки даже с помощью ваших намеков на решение, то может иметь смысл оставить на время лингвистическую задачу и вернуться к ней дома или на другом уроке. Многие такие задачи допускают решение в несколько подходов.

Чтобы дети сразу обратили внимание на особенности лингвистических задач, мы привели развернутое указание, в котором содержится несколько полезных соображений. Итак, какие же правдоподобные практические языковые соображения работают при решении аналогичных задач? Мы исходим из того, что если языки родственны, то они должны иметь что-то общее. Например, некоторые слова могут быть близки по звучанию или написанию. Конечно, это относится не ко всем словам, поэтому нам придется использовать всю информацию, которую можно извлечь из наборов слов.

Начнем со слова «дерево», о котором дана явная подсказка в указании. Оно в каждом наборе встречается лишь однажды, значит, «ИГЛОЛИСТНО ДЪРВО» - это «ХВОЙНОЕ ДЕРЕВО». Теперь мы знаем, как будет по-болгарски «ХВОЙНОЕ» и можем найти болгарское «ХВОЙНЫЙ ЛЕС». Это «ИГЛОЛИСТНА  ГОРА». Значит, лес по-болгарски – это «ГОРА». Больше такого слова в наборе нет, но зато есть несколько слов, похожих на однокоренные – «ГОРСКА», «ГОРСКИ». Можно предположить, что они означают что-то близкое к «ЛЕСНАЯ», «ЛЕСНОЙ». Причем для начала предположим самое простое (и естественное), что «ЯГОДА» означает действительно ягоду. Тогда «ГОРСКА ЯГОДА» - это «ЗЕМЛЯНИКА» (лесная ягода), а «ГОРСКИЙ ПОЯС» - «ЛЕСОПОЛОСА». У нас есть еще одно болгарское словосочетание со словом «ЯГОДА» - «ГРАДИНСКАЯ ЯГОДА», оно означает, видимо, «КЛУБНИКА», потому что больше ягод в русском наборе просто нет. Но что тогда означает «ГРАДИНСКАЯ»? Рассуждая таким образом, можно дойти до полного решения. Как видите, путь не близкий, желательно не торопить детей и, конечно же, не подсказывать.  Вполне возможно, если такую задачу ребенок будет решать несколько месяцев, допустимо, чтобы дети решали ее по двое или в группе. В таких задачах процесс важнее результата, ведь в ходе самостоятельного решения таких задач дети получают колоссальный лингвистический опыт, который им пригодится не только в обучении, но и в жизни.

Ответ:

ЛЕДЕНА ПЛАНИНА  -  АЙСБЕРГ

ИГЛОЛИСТНО ДЪРВО – ХВОЙНОЕ ДЕРЕВО

ГОРСКА ЯГОДА – ЗЕМЛЯНИКА

ГОРСКИ ПОЯС – ЛЕСОПОЛОСА

ИГЛОЛИСТНА ГОРА – ХВОЙНЫЙ ЛЕС

ГРАДИНА – САД

ПЛАНИНСКА ВЕРИГА – ГОРНАЯ ЦЕПЬ

ГРАДИНСКА ЯГОДА – КЛУБНИКА

ГОРОЛОМ – БУРЕЛОМ