Компьютерное дополнение к курсу Информатика 6. 2017

Урок 17. «Выравнивание, решение необязательных и трудных задач»

Без сомнения, многие учителя традиционно проводят перед контрольной работой уроки обобщающего повторения и очень хорошо знают, что это такое. Однако в нашем курсе традиционными являются именно уроки выравнивания, которые проводятся не до, а после контрольной работы. По этому поводу хотелось бы дать некоторые разъяснения. В курсе начальной школы мы планировали уроки выравнивания в конце каждой четверти на протяжении всех учебных лет. Это уроки, на которых не изучаются новые листы определений, на них только решаются разнообразные задачи.

Кто-то из вас, может быть, сочтет более предпочтительным употребить этот час на подготовку к контрольной работе. Но проблема в том, что на уроке подготовки к контрольной работе и у детей, и у учителя очень конкретная и единственная цель – справиться с контрольной работой. При этом контрольная работа имеет обычно средний уровень сложности, на который учитель и ориентируется при планировании такого урока. Оптимально загруженным на таком уроке фактически будет только средний ученик: для сильного учащегося задачи будут слишком простыми, а для слабого – слишком сложными. Поэтому со слабыми детьми учитель обычно работает индивидуально, а сильные так и не достигают высот, соответствующих их возможностям.

Мы же, напротив, рассчитываем на то, что дети справятся с нашими контрольными работами без специального урока подготовки к контрольной работе, который обычно выливается в простое натаскивание на определенные типы задач. Контрольная работа – это лишь проходной мгновенный срез знаний, а не финишный итог. Итоги контрольной работы – это как раз индикатор, на который вы будете ориентироваться, выстраивая индивидуальные траектории обучения и, в частности, подбирая набор и содержание задач урока выравнивания для каждого ученика. Поэтому мы предлагаем провести урок выравнивания после контрольной работы.

На уроке выравнивания можно в полной мере реализовать дифференцированный подход и спланировать индивидуальные траектории обучения для каждого ученика. Ясно, что и целеполагание на этом уроке для разных учащихся может быть разным.  Для учащихся, которые не справились с контрольной работой (или справились очень слабо), этот урок – возможность достичь базового уровня знаний, достаточного для дальнейшей работы с курсом. Для таких детей стоит выбирать только стандартные задачи из числа обязательных, того же уровня, что и задачи контрольной работы. Для средних детей, справившихся с контрольной работой на твердую тройку или четверку, данный урок – урок решения дополнительных задач. На таком уроке «середнячки» имеют возможность продвинуться в изучении данной темы, «взять новую высоту», научиться решать более сложные задачи. Для таких детей набор задач будет комбинироваться из числа обязательных задач посложнее и необязательных задач попроще. Для сильных детей, которые с контрольной работой справились легко (не ниже твердой четверки) данный урок – урок решения трудных задач. Для них предназначены задачи, которые мы будем характеризовать как «сложные». Все эти задачи выше уровня задач контрольной работы и даже многих задач, встречавшихся в учебнике.

Вполне возможно, что вы не захотите делить учащихся строго на три означенные группы, а каждому учащемуся подберете собственный набор задач. Это будет замечательно. Мы ведь не знаем каждого из ваших детей, поэтому даем здесь лишь общие советы, подходящие для основной массы детей. Конечно, нам бы хотелось, чтобы все дети на таком уроке работали полностью самостоятельно, но иногда учителю все-таки приходится оказывать помощь. Обращаем ваше внимание, что помощь должна быть минимальной. Особенно это касается сильных детей, им будет достаточно намека на путь решения. Организовать такой урок можно следующим образом. Чтобы не привлекать внимание детей к тому, что вы делите их на группы по силе (кому-то это может показаться обидным), можно на каждого ребенка заготовить бумажку с номерами 5-6 задач из учебника, которые вы предлагаете ему решить. По мере работы с задачами для кого-то задание, возможно, придется несколько поменять – усложнить или, наоборот, упростить.

Повторим еще раз – выбор вида урока (урок выравнивания или урок итогового повторения) целиком остается на усмотрение учителя. Набор задач подобран нами с таким расчетом, чтобы по ним можно было провести и тот, и другой урок. При наличии времени можно провести и оба урока, задач имеется достаточно. Если какие-то задачи (даже обязательные) с этих страниц останутся нерешенными, это тоже не страшно. Конечно, классам, изучавшим наш курс в начальной школе, мы рекомендуем провести урок выравнивания, поскольку дети к таким урокам привыкли и практика показывает, что детям такие уроки нравятся. Если класс изучает курс первый год, то выбор зависит как от силы и подготовленности класса, так и от предпочтений учителя.

    Задача 82. Повторяем исполнителя Робота и алгоритмы для него. Вообще говоря, алгоритмов, переводящих Робота из клетки А в В, очень много. Но мы ограничены небольшим полем, и, чтобы ребенок не выдумывал сложных алгоритмов, дается ограничение – не больше 10 команд. На деле это означает, что Робот всегда будет делать шаг, приближающий его к цели и никогда – отдаляющий его от цели. В этом случае на нашем маленьком поле он сможет повторить этот алгоритм из всех упомянутых в условии точек. Даже при этих ограничениях подходящих алгоритмов будет несколько. Однако сам алгоритм, по сути, для нас не важен. Важно правильно перенести его результат при других исходных позициях. Сильные дети, вполне возможно, сумеют сделать это умозрительно. Ну а слабые пусть решают задачу в лоб: пишут подходящий алгоритм, а потом выполняют его из всех нужных точек. Второй вопрос задачи может представлять некоторую сложность, особенно для слабых учащихся. Итак, может ли быть в алгоритме четное число команд? Посмотрим внимательно на поле Робота. Чтобы попасть из А в В, Роботу необходимо сместиться на 4 клетки по горизонтали и на 5 – по вертикали. В сумме это 9 команд, задающих кратчайший путь из А в В. Так что восьми команд не хватит заведомо. Что же касается 10, то любая 10-ая команда должна повлечь 11-ую, т.к. она уведет Робота с кратчайшего пути и ему надо будет на него вернуться. Поэтому ответ на вопрос б): нет, не может.

     Задача 83. Необязательная. В целом задача несложная и для своего решения не требует знания французского и итальянского языков. Проще всего решать эту задачу, спускаясь по таблице сверху вниз, а не наоборот. Родственные слова отыскиваются довольно легко. Единственное исключение – последние две строчки: samedi и dimanche (фр.) и  sabato и domenica (итал.). На латыни и суббота, и воскресенье начинаются на s, поэтому могут возникнуть сомнения, в какую строку поставить samedi и  sabato. Но тут на помощь приходит, как ни странно, русский язык: sabato настолько напоминает нашу «субботу», что все сомнения сразу исчезают.

     Задача 84. Повторение тем «Дерево перебора вариантов» и «Поиск кратчайшего пути». Как видите, здесь мы предлагаем детям задачу с практическим содержанием и, как во всякой практической задаче, здесь необходимо выполнить перенос старых знаний на новые объекты. Чаще всего реальные (практические) объекты не могут полностью соответствовать научным, абстрактным объектам. Так, схема метро, конечно, очень похожа на граф, но не полностью отражает внутреннюю структуру нашей задачи. Например, пересадки на схеме метро не показаны отдельными ребрами, ведь обе станции показаны общим кружком. На самом деле с точки зрения затраченного времени (а именно так мы анализируем данный граф) нужно было бы нарисовать две отдельные станции, а между ними переход, который займет 5 минут. Поэтому при построении дерева перебора схему метро надо анализировать не формально (как мы делали в задаче 59 и на листе определений "Поиск кратчайшего пути"), а учитывая практическое содержание задачи. Кроме того, надо сразу принимать во внимание, что здесь надо выписать не маршруты, а вершины графа, а дерево перебора мы будем все равно строить для перебора всех маршрутов. При этом маршрут мы будем заканчивать, как только он выйдет за рамки отведенного времени (11 минут). Заметим, что и в этой задаче нет смысла рассматривать маршруты с возвращениями на одну и ту же станцию, ведь если на этой станции мы уже побывали, то она будет входить в решение (а больше нас ничего и не интересует).

Итак, мы едем от станции «Новочеркасская» ‒ она и будет корневой бусиной. Из нее можно попасть на станцию «Ладожская» и «Пл. Ал. Невского II», они и будут вершинами второго уровня. Если принимать во внимание договоренность не возвращаться на станции, где мы уже были, то с «Ладожской» можно попасть только на «Пр. Большевиков», а дальше на «ул. Дыбенко». С «Пл. Ал. Невского II» можно попасть на «Пл. Ал. Невского I» и «Лиговский пр.». По ходу перебора нужно на каждом уровне считать длину получившегося пути, чтобы не превысить означенное в задаче время. Так, очень быстро становится ясно, что из каждой станции третьего уровня можно уже либо проехать одну станцию, либо сделать одну пересадку, на большее не хватит времени. Значит, наше дерево перебора маршрутов состоит из четырех уровней, в нем оказывается ровно 4 пути (маршрута):

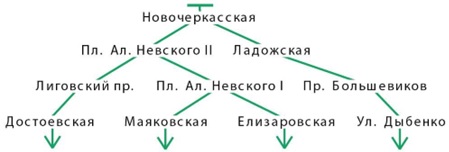
Теперь необходимо из дерева перебора маршрутов выписать в ответ все станции, которые в нем есть (кроме «Новочеркасской»).

Ответ: «Ладожская»,  «Пл. Ал. Невского II», «Пр. Большевиков», «ул. Дыбенко», «Пл. Ал. Невского I», «Лиговский пр.», «Достоевская», «Елизаровская», «Маяковская».

Задача 85. Лучше решать эту задачу, построив дерево перебора всех вариантов. Поскольку длина цепочки равна 2, в дереве будет 2 уровня. На первом уровне располагаем два элемента – бусины мешка К. Каждый элемент 1-го уровня будет иметь два следующих – опять же, бусины мешка К. Итого листьев в нашем дереве – 4. Значит, в ответе будут 4 разные цепочки.

     Задача 86. Необязательная. Эта задача похожа на задачу 63, но гораздо объемнее. Однако решается она совершенно аналогично – дерево надо представить и описать, а затем ответить на вопрос задачи. Итак, в номере 1 буква, 3 цифры и еще две буквы, значит, всего в нашем дереве будет 6 уровней. На первом уровне 28 корневых букв (поскольку Ё, Й, Ъ, Ы, Ь не используются). За каждой из корневых букв может идти одна из десяти цифр, значит, на втором уровне будет 28×10 цифр. За каждой из цифр второго уровня будут идти снова десять цифр, значит, на третьем уровне будет уже 28×10×10 цифр, а на четвертом - 28×10³ цифр. За каждой из этих цифр будут следовать в дереве 28 букв, значит, на пятом уровне будет 28²×10³ вершин. За каждой из них снова будут следовать 28 букв.

Ответ: в одном регионе существует 28³×10³ (21 952 000) автомобильных номеров.

Задача 87. Необязательная. Это типичная задача на сообразительность и смекалку. Ключ к ее решению в том, чтобы правильно представить себе процесс деления амеб. Ответ, который сразу приходит в голову детям, – «полчаса»  – оказывается неверным. На самом деле, чтобы одна амеба превратилась в две, нужна одна минута, поэтому если мы вместо одной амебы положим две, то сэкономим ровно1 минуту общего времени.

Ответ: потребуется 59 минут.

Задача 88. Повторение исполнителя Робот. Если посмотреть внимательно на алгоритм, становится ясно, что Робот нарисует некую спираль, причем ряды закрашенных клеток будут чередоваться с незакрашенными. Поскольку повторного закрашивания клеток здесь не будет, то число закрашенных клеток будет в точности совпадать с числом команд закрасить. Вот рисунок после выполнения Роботом алгоритма узор3:

Задача 89. Составление алгоритмов для Робота с использованием циклов. Ребят может смутить тот факт, что неизвестен вспомогательный алгоритм узор4. На самом деле для нас совершенно не важно, какой рисунок получается в результате его выполнения. Важно представить себе поле 20х20, расчлененное на фрагменты по 4х4 клетки. Таких фрагментов будет по 5 в каждом из пяти рядов. Таким образом, Робот выполняет алгоритм узор4, затем смещается в левый верхний угол следующего фрагмента, и так – до конца ряда. Далее возможны варианты. Можно следующий ряд делать, смещаясь после каждого фрагмента в противоположную сторону (в этом случае у нас получится 5 независимых циклов), а можно вернуть Робота снова на левый край поля и следующий ряд делать в том же направлении, что и первый. В этом случае возникает возможность использовать более сложную структуру вложенных циклов. Типичная ошибка в подобных алгоритмах состоит в том, что дети, не задумываясь, пишут:

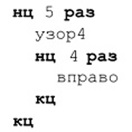
На самом деле в результате выполнения такого алгоритма Робот, действительно, нарисует ряд из 5-ти фрагментов, соответствующих алгоритму узор4,   но ко всему прочему он еще лишний раз сместится вправо, выйдя за пределы поля 20х20 на 1 клетку. Мы не можем этого допустить по той простой причине, что поле у нас ограничено 20-ю клетками. Поэтому вышеприведенный фрагмент более правильно переписать следующим образом:

Далее должны следовать команды, переводящие Робота в позицию для выполнения следующего ряда фрагментов 4х4 по одному из описанных выше вариантов.

Вот один из вариантов ответа:

Задача 90. Аналогичные задачи ребята уже решали. Рассуждения тут довольно простые. Если Кузнечик оказался в той же точке, в которой был до выполнения алгоритма, значит, в результате пяти команд он сделал вперед столько же шагов, сколько и назад. То есть количество команд «вперед 3», умноженное на 2, равняется количеству команд «назад 2», умноженному на 3: 3 ∙ 2 = 2 ∙ 3.  В сумме это дает 5 команд, что и требуется по условию. Итак, искомый алгоритм (назовем его «топтание на месте») будет выглядеть так:

Меньше пяти команд использовать не получится, в этом легко убедиться, попытавшись «уравновесить»  1 команду «вперед 3». Три команды «вперед 3» «уравновесить вообще не удастся, т.к. нечетные числа на 2 не делятся. А чтобы «уравновесить» 4 команды «вперед 3», потребуется уже 6 команд «назад 2», что в сумме составит 10 команд. Вообще говоря, программ с таким свойством существует бесконечное множество (количество команд «вперед 3» и «назад 2» определяется последовательным умножением на 2 числа команд в нашем алгоритме топтание на месте), но с общим количеством команд, равным 5, такой алгоритм единственный.

Задача 91. Необязательная. Аналогичные задачи дети уже решали. Найдем общее число мест, которые занимают ученики класса во всех трех кружках: 17+30+13=60. Пять человек посещают 3 кружка одновременно ‒ это в сумме 15 мест. Вычтем их из общего числа, получим: 45 мест на 30  детей. Каждый из них ходит, по крайней мере, в 1 кружок ‒ это 30 мест. Вычтем их из 45, получим 15. Итак, 15 детей ходят в 2 кружка, значит, 30‒15=15 детей ходят только в 1 кружок.

Задача 92. Необязательная.