Компьютерное дополнение к курсу Информатика 6. 2017

Уроки 11–12. «Дерево перебора вариантов. Дерево перебора подмножеств»

Как мы говорили, в курсе 6 класса назначение текстов на листе определений становится самым разнообразным. На этом уроке мы снова встречаем лист определений нового вида. Данный лист определений содержит немного новой лексики и не содержит каких-либо определений.

Почти весь объем листа определений (довольно большого!) составляют примеры задач на перебор и их решений с помощью деревьев. Поэтому работа с данным листом определений заключается в том, чтобы разобраться в приведенных примерах.

Применение дерева для перебора вариантов – пожалуй, одно из самых распространенных его приложений. Здесь древесная структура диктуется логикой самой задачи. При этом, строя дерево перебора, мы не просто считаем, сколько должно получиться таких последовательностей (как требуется в классической комбинаторной задаче), а строим все объекты, решая задачу из современной комбинаторики. Если мы перебираем объекты, которые можно представить в виде последовательностей, то решение становится совсем прозрачным. На первом уровне дерева мы помещаем все элементы, которые могут быть первыми в искомых последовательностях. На втором уровне для каждого из элементов первого уровня мы рисуем его детей – элементы, которые могут стоять вторыми в последовательности при условии, что первым выбран данный элемент. Затем рисуем детей элементов второго уровня – элементы, которые могут стоять третьими, при условии что первым и вторым выбраны данные элементы. Так мы двигаемся, пока число уровней не станет равно длине искомой последовательности. В результате получаем дерево перебора – дерево, все пути которого представляют собой искомые последовательности. Выписав их, получаем множество вариантов.

По описанному алгоритму мы решали Задачу 1 и Задачу 2 листа определений. В задаче 1 способом падения двух монет мы считаем, по сути, стороны монет, которые мы увидим, когда обе монеты уже упадут на стол. Поэтому в задаче на перебор способов падения двух монет порядок падения монет на самом деле не важен, то есть, по сути, получаются не последовательности монет, а множества. Но множества не так удобно перебирать, как последовательности, поэтому в этой задаче мы привносим порядок искусственно. Чтобы объяснить ребятам упорядоченность монет, мы в условии используем временные понятия – подкинули сначала, подкинули потом. На самом деле ответ (число способов падения монет) не зависит от того, какую монету кидать сначала, а какую – потом, можно монеты кидать и одновременно. Действительно, в данном случае получившееся число последовательностей равно числу разных множеств, составленных из элементов этих последовательностей. Так ситуация будет складываться не всегда. Например, если мы возьмем две одинаковые монеты и подкинем их одновременно, то способов, по сути, будет не 4, а лишь три: два орла, две решки, один орел и одна решка.

В задаче 2 мы ведем перебор чисел (последовательностей цифр), поэтому дерево снова появляется естественно. На первом уровне дерева мы располагаем все цифры, которые могут быть первыми цифрами числа, в данном случае это 2, 4, 6. Теперь расставим числа на втором уровне. Поскольку цифры искомых чисел могут повторяться, то вторая цифра не зависит от первой и после каждой первой цифры снова может идти одна из трех данных цифр. Аналогично ситуация будет складываться и с третьей цифрой. Получаем дерево Б, множество путей которого – множество искомых чисел. Мы не стали здесь явно выписывать все искомые числа, ведь ребята сами умеют это делать достаточно хорошо. Если такое упражнение покажется вам полезным, попросите ребят выписать в тетрадь по дереву Б все такие числа.

Наиболее сложным оказывается третий пример с листа определений (задача 3). Действительно, оказывается, множества гораздо труднее перебирать с помощью дерева, чем последовательности. Причина – отсутствие порядка элементов в множестве. Порядок, конечно, можно внести искусственно, но некоторых элементов в искомых множествах может просто не быть. Значит, надо строить дерево перебора подмножеств как-то иначе, чем мы делали в задачах 1 и 2. Итак, на основании чего будет происходить ветвление нашего дерева или какие у нас будут появляться варианты? В каждом из подмножеств данного множества каждая бусина исходного множества может быть или не быть, это и будет принципом ветвления. Как видите, при построении дерева Д мы снова выбрали некий произвольный порядок. Из дальнейшего решения видно, что он не влияет на ответ. В дереве Д вершинами являются, по сути, надписи (или утверждения) – «в множестве есть синяя треугольная бусина», «в множестве нет желтой круглой бусины» и т. д. Мы решили, что нагляднее изобразить эти надписи в виде значков – «есть» или «нет»  – внутри бусин. Поскольку вершины – не элементы множеств (а пометки), то множество подмножеств не равно множеству путей этого дерева. Но множество путей позволяет построить искомое множество – каждому пути дерева Б соответствует некоторое подмножество В. На первый взгляд предложенное решение может показаться слишком сложным, но так будет лишь до тех пор, пока исходное множество будет достаточно небольшим. Как только множество будет состоять более чем из 5 элементов, мало кто из детей сможет перебрать все его подмножества и не запутаться. Данный алгоритм хорош тем, что помогает даже в таких сложных ситуациях.

Большинство задач, которые мы предлагаем детям на данном уроке, имеют много общего. В частности, одной из классических комбинаторных задач является задача на построение из элементов данного множества всех последовательностей данной длины. При этом дерево перебора отражает последовательность нашего выбора элементов из данного множества. Но заметим, что чаще всего выбор у нас будет двух типов – с возвращениями (повторениями) и без возвращений (повторений). В первом случае мы, выбрав элемент из множества, затем возвращаем его обратно. Поэтому на следующем этапе этот же элемент может быть выбран снова. В результате последовательность может содержать одинаковые (повторяющиеся) элементы. Во втором случае мы, выбрав элемент из множества, изымаем его из множества и, соответственно, из дальнейших выборок. В результате все элементы в последовательности оказываются разными.

 

Задача 44.  Эта задача аналогична задаче 1 с листа определений, поэтому ее решение может служить для проверки качества усвоения листа определений. Постарайтесь не помогать детям чрезмерно. Ребятам, у которых возникли проблемы, нужно посоветовать еще раз разобрать решение задачи 1. Как видно из указания к этой задаче, дерево здесь будет выглядеть достаточно схематично, но это не важно. Важно, чтобы дети хорошо ориентировались в своем дереве и могли ответить по нему на вопрос задачи.

Ответ: существует 8 вариантов падения трех разных монет.

Задача 45. В этой задаче, возможно, придется кому-то из детей помочь с построением дерева, ведь это первая новая по содержанию задача на перебор вариантов. Порассуждайте вместе с ребенком о том, какие цифры могут быть в искомых числах и как нужно строить дерево. Искомые числа – двузначные, значит, в дереве будет два уровня. Какие цифры могут стоять на первом уровне? Все, кроме 0, 2 и 3. Какие цифры могут стоять на втором уровне дерева? После каждой цифры первого уровня должны стоять только четные цифры, но не 0 и не 2. Значит, это цифры: 4, 6, 8. Получаем дерево перебора:

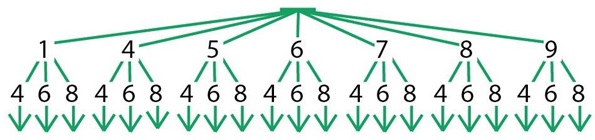
Теперь выписываем искомые числа и отвечаем на вопрос задачи.

Ответ: 21 число: 14, 44, 54, 64, 74, 84, 94, 16, 46, 56, 66, 76, 86, 96, 18, 48, 58, 68, 78, 88, 98.

Задача 46. Эта задача аналогична задаче 3 с листа определений, поэтому ограничьтесь в своей помощи лишь самыми общими советами (или предложением еще раз разобрать задачу 3). Вершинами дерева перебора подмножеств снова должны быть пометки: «есть 1», «нет 1», «есть 2», «нет 2» и т.д. Если ребенок слабый, то лучше посоветовать ему после построения дерева выписать сначала все его пути, а затем уже выписывать все подмножества множества W. Сильные учащиеся, скорее всего, смогут выписать все подмножества прямо с дерева перебора.

Ответ: подмножества множества W: пустое; 1; 2; 3; 4; 1, 2; 1, 3; 1, 4; 2, 3; 2, 4; 3, 4; 1, 2, 3; 1, 2, 4; 1, 3, 4; 2, 3, 4; 1, 2, 3, 4.

Задача 47.  Это довольно любопытная задача, находящаяся на стыке информатики, комбинаторики и языка. В разговорном языке такие задачи перед нами встречаются редко (за исключением курьезных ситуаций), но есть несколько языковых игр, построенных как раз по этому принципу. Например, игры, где несколько участников пишут подлежащее «Кто?», меняются записками, пишут сказуемое «Что делает?», меняются записками и т.д. Все получившиеся в результате предложения зачитываются вслух, и выбирается самое смешное, самое фантастическое, самое реалистическое и т.д. «Соль» игры в том, что с точки зрения языка и грамматики предложения чаще всего оказываются построенными верно, а вот с точки зрения содержания, логики и смысла получается по-разному. В данной задаче получается похожая ситуация, только слова в множествах мы подбирали так, чтобы все получившиеся предложения были не только грамматически верными, но и вполне осмысленными. Дети продолжат игры с комбинированием слов в проекте «Забавное стихотворение».

Несмотря на внешнюю необычность, данная задача – типичная задача на перебор вариантов. Она аналогична задаче 2 (с листа определений), при условии что цифры мы берем не из одного и того же множества, а из разных. Поэтому позвольте ребятам и с этой задачей справиться самостоятельно. Сначала, как обычно, нужно построить дерево перебора. На первом уровне должны находиться слова из мешка Р (подлежащие). После каждого из них должны идти оба слова из мешка Q (сказуемые). После каждого глагола должны идти три слова из мешка R (дополнения). Получаем дерево перебора.

Теперь выписываем искомые последовательности. В данном случае их получается много – 24 последовательности, поэтому решение данной задачи займет довольно много времени. При дефиците времени на уроке можно предложить эту задачу для домашней работы.

Ответ:

КАТЯ СЛУШАЕТ СКАЗКУ.

КАТЯ СЛУШАЕТ РАССКАЗ.

КАТЯ СЛУШАЕТ СТИХИ.

КАТЯ ЧИТАЕТ СКАЗКУ.

КАТЯ ЧИТАЕТ РАССКАЗ.

КАТЯ ЧИТАЕТ СТИХИ.

ДАША СЛУШАЕТ СКАЗКУ.

ДАША СЛУШАЕТ РАССКАЗ.

ДАША СЛУШАЕТ СТИХИ.

ДАША ЧИТАЕТ СКАЗКУ.

ДАША ЧИТАЕТ РАССКАЗ.

ДАША ЧИТАЕТ СТИХИ.

ПЕТЯ СЛУШАЕТ СКАЗКУ.

ПЕТЯ СЛУШАЕТ РАССКАЗ.

ПЕТЯ СЛУШАЕТ СТИХИ.

ПЕТЯ ЧИТАЕТ СКАЗКУ.

ПЕТЯ ЧИТАЕТ РАССКАЗ.

ПЕТЯ ЧИТАЕТ СТИХИ.

МИША СЛУШАЕТ СКАЗКУ.

МИША СЛУШАЕТ РАССКАЗ.

МИША СЛУШАЕТ СТИХИ.

МИША ЧИТАЕТ СКАЗКУ.

МИША ЧИТАЕТ РАССКАЗ.

МИША ЧИТАЕТ СТИХИ.

Задача 48. Необязательная. На первый взгляд эта задача напоминает арифметическую сюжетную задачу. На самом деле это классическая задача на перебор. Ключ к ее решению в понимании того, что монеты, которые Вова достал из кармана, – это подмножество данного множества монет (1 к., 5 к., 10 к., 50 к.). Если нам нужно указать все варианты, значит, надо перебрать все подмножества данного множества. Тогда для начала нужно построить дерево перебора, аналогичное тому, которое мы строили в задаче 46 (с точностью до замены цифр на данные числа). После того как дерево перебора будет построено, надо для каждого пути дерева посчитать соответствующую сумму денег.

Ответ: у Вовы в руке может быть: 0 к., 1к., 5к., 6к., 10к., 11к., 15к., 16к., 50к., 51к.,  55к., 56к., 60к., 61к., 65к., 66к.

Задача 49. Как любая задача о формулировке правила, для кого-то из ребят эта задача может оказаться сложной. Здесь нужно придумать правило, по которому построено дерево перебора. Если кто-то из детей совсем не знает с чего начать, попросите его сравнить дерево К с деревом Б, которое мы строили в задаче 2 листа определений. Может, кому-то из детей будет полезно выписать все пути дерева К и попробовать понять, что у них общего. Действительно, все эти числа состоят только из цифр 2, 4, 6, причем ни в одном числе нет двух одинаковых цифр.

Заметим, что данная задача и задача 2 с листа определений действительно имеют много общего. Обе эти задачи – задачи на построение последовательности длины 3 из элементов (цифр) данного множества, но в задаче 2 выбор цифр производится с возвращениями, а в данной задаче – без возвращений.

Ответ: постройте множество всех трехзначных чисел, составленных из цифр 2, 4, 6, в которых нет двух одинаковых цифр.

Задача 50. Повторение алгоритмов для Удвоителя. Второй вопрос, несмотря на то что в ответе должно получиться большое число, совсем простой: дважды прибавив к 0 единицу, далее просто умножаем последовательно на 2. В первом вопросе приходится все время перемежать умножение на 2 и прибавление 1.

Задача 51. Повторение площади многоугольника на сетке. В данном случае площадь можно найти только вычитанием из общей площади прямоугольника площадей «лишних» фигур (прямоугольных треугольников).

Ответ: площадь многоугольника F 13 с половиной ед. кв.

Задача 52. Достаточно сложная задача, которая подойдет для сильного и среднего ребенка. Здесь не построишь дерево перебора по общей схеме, иначе оно будет очень большим. В этой задаче лучше комбинировать построение дерева перебора с рассуждениями, которые позволят по ходу отбрасывать неподходящие варианты. Это сделает перебор не только обозримым, но и совсем небольшим. Итак, какой может быть первая цифра искомых чисел? Числа должны быть больше 500, значит, первая цифра больше 4, но сумма цифр равна 9, значит, первая цифра меньше 9 (число 900 нам не подходит, ведь оно четное). Значит, рисуем на первом уровне 5, 6, 7 и 8. Теперь для каждой цифры нужно подобрать возможные следующие цифры. Ясно, что не все вторые и третьи цифры нам подойдут, поэтому лучше не писать все возможные варианты сразу в дерево, а проводить перебор в уме и писать лишь варианты, подходящие по условию. Перебираем цифры, следующие за 5 в порядке возрастания (чтобы не потерять решений). Берем ноль, находим по сумме цифр третью цифру, получаем 504 – не подходит (четное число). Берем вторую цифру 1, подбираем для нее по сумме цифр третью цифру, получаем 513. Такое число нам подходит, записываем такой путь в дерево и продолжаем перебор. В результате находим только два варианта следующей цифры после 5 – 1 и 3. Аналогично ищем цифры, следующие после 6, 7 и 8. Затем выписываем в ответ все пути получившегося дерева.

Ответ: 513, 531, 603, 621, 711, 801.

Задача 53. Здесь требуется построить все последовательности длины 2 из элементов данного множества, причем выбор происходит без возвращений (поскольку буквы должны быть разными). Значит, в дереве перебора два уровня, и на первом уровне находятся все пять букв данного множества. Дети каждой буквы первого уровня – все оставшиеся буквы исходного мешка (исключая данную букву). Таким образом, искомое множество состоит из 20 последовательностей.

Ответ: АБ, АВ, АГ, АД, БА, БВ, БГ, БД, ВА, ВБ, ВГ, ВД, ГА, ГБ, ГВ, ГД, ДА, ДБ, ДВ, ДГ.

Задача 54. Задача похожа на задачу 1 с листа определений, поэтому старайтесь не помогать детям чрезмерно. Можете дать ребятам несколько технических советов, которые помогут им сэкономить время при построении дерева. Конечно, монету прорисовывать не нужно, достаточно нарисовать кружок с пометками О (орел) или Р (решка). Игральную кость тоже прорисовывать не нужно, достаточно нарисовать квадрат, написав внутри число точек. Тогда дерево можно построить довольно быстро. В нем будет два уровня бусин. На первом уровне будут находиться две стороны монеты, а после каждой из них – шесть сторон игральной кости.

Ответ: монета и игральная кость могут упасть 12 разными способами.

Задача 55. Задача о переборе вариантов. Здесь также удобно для решения нарисовать дерево перебора. Поскольку нужно построить последовательности длины 3, дерево будет иметь три уровня. Цифры в последовательностях могут повторяться, поэтому каждый элемент, кроме листьев, будет иметь две следующие – 0 и 1.

Ответ: всего последовательностей – 8.

Задача 56. Задача о переборе вариантов. Цифры в выборках повторяются, но поскольку, в отличие от множеств, числа представляют собой упорядоченные последовательности, то и пары выборок типа 5-5-4 и 4-5-5 будут разными числами. Поэтому при построении дерева отслеживать и отбрасывать совпадающие выборки не придется.

Ответ: всего разных чисел будет 27.

Задача 57. Необязательная. Составление алгоритма для Робота. Скорее даже не составление, а редактирование ранее написанного в соответствии с новым заданием. Переписывать старую программу всегда сложнее, чем писать заново. Если не вставлять в алгоритм заведомо лишние команды закрасить, то всего дважды закрашенных клеток будет 8.

Задача 58. Необязательная. Достаточно интересная и развлекательная практическая задача. Примерно такой деятельностью приходится заниматься рестораторам, составляя различные варианты меню бизнес-ланчей, комплексных обедов и т.д. Что касается завтраков, то здесь в кафе «Таверна» вариантов не слишком много, всего 6. С обедами ситуация несколько сложнее, здесь получается 16 вариантов.