Компьютерное дополнение к курсу Информатика 5. 2017

Урок 29. «Исполнитель Робот. Прямое и программное управление»

Исполнитель Робот. Обстановки

Исполнитель Робот обладает самыми богатым набором  возможностей по сравнению с остальными исполнителями, рассматриваемыми в нашем курсе. С Роботом связаны два важных новых понятия: команда-вопрос и обстановка. С командами-вопросами ученики подробно будут знакомиться позже, в курсе 6 класса в разделах, посвященных конструкциям повторения и ветвления. Эти команды позволяют создавать программы, которые по-разному ведут себя при разных начальных данных. Понятие «обстановка» имеет примерно тот же смысл, что и в обыденной жизни, Например, обстановкой для лунохода является поверхность Луны, а для станка-автомата – заготовка детали. Для формальных исполнителей понятие обстановки также формализуется. Для Робота обстановка – это прямоугольник заданного размера, в котором указано, где стоят стены и какие клетки закрашены. Для исполнителя Робот системы Кумир в каждой клетке обстановки Робота еще могут быть заданы температура и радиация, но в задачах нашего курса эти возможности не используются.

Прямое и программное управление

С программами ученики познакомились на уроке 25 при работе с исполнителем Перевозчик. В пояснениях к тому уроку мы подробно разбирали роль командира при выполнении программ, командиром может быть как человек, так и компьютер (в современном мире компьютеры в этой роли бывают чаще). Воспользуйтесь этими пояснениями для обсуждения материала урока в классе.

Задача 179. Простая задача на понимание материала листа определений. Никаких ограничений на программы здесь нет, поэтому они не обязательно должны быть оптимальными и могут содержать любое количество команд. Например, годится и такая программа:             

          вправо

          вправо

          вверх

          вниз

          вправо

          вправо

          вниз

          влево

          влево

Задача 180. Задача на понимание терминологии, введенной на листе определений. Как и в предыдущей задаче, не стоит требовать от детей минимизации длины программы. Главное, чтобы Робот смог написанную программу выполнить и при этом в результате выполнения программы попал в клетку D.

Задача 181. В этой задаче помимо движения Робота, используется и команда закрасить. Понятно, что если Роботу надо закрасить клетку, он должен в нее попасть. Как именно обойти все клетки и раскрасить их – решать, конечно, ребенку. Но сильного ученика уже можно попросить написать программу покороче – чтобы Робот не делал лишних шагов.

Задача 182. Качественная задача о Роботе. И в той, и в другой программе Робот выполнит команду  по 5 раз. Но при этом может оказаться, что некоторые клетки Робот закрасит два или больше раз – таким образом в результате выполнения программы на поле будет закрашено меньше 5 клеток. Поэтому, чтобы выяснить, сколько же клеток окажется закрашенными, надо выполнить программы А и Б. Выполнив программу на черновике, выясняем, что после выполнения программы А Робот закрасит 5 клеток, а после выполнения программы Б – 4 клетки.

Задача 183. Компьютерный практикум (см. комментарий к задаче 142). Вы можете составить задачи сами или воспользоваться задачами, данными в конце учебника.

Задача 184. Необязательная. Чтобы ответить на вопрос задачи, надо «откручивать» выполнение программы с конца. После выполнения последней команды получилось число 512, значит предыдущим результатом было число 256, перед ним – число 128, перед ним – 64, 32, 16, 8, 4 и 2. Итак, всего было 9 удвоений – было выполнено 9 команд умножь на 2.

Задача 185. Необязательная. Задача может испугать слишком большой степенью обобщения. Но, «глаза боятся – руки делают». Вспомним: решая задачу 171, мы написали программу, которая заставила Кузнечика попасть в каждую точку отрезка прямой от 0 до 5:

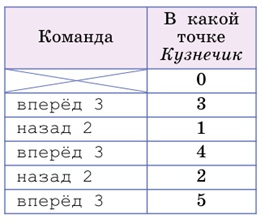
Посмотрим внимательно, как устроена эта программа. Выполнив две первые команды, Кузнечик попадает из точки 0 в точку 1. Выполнив снова такую же пару команд (вперёд 3, назад 2), он попадет из точки 1 в точку 2. Становится ясно, что выполняя эти пары команд, он может продвинуться на любое расстояние вправо – попасть в любую точку правой части числовой прямой. 

Теперь попытаемся составить программу, которая переводит Кузнечика на один шаг влево – если нам это удастся, то аналогично с правой частью числовой прямой, Кузнечик сможет попасть в любую точку левой части числовой прямой, выполним нашу программу столько раз, сколько потребуется. Составить такую программу несложно:

          вперёд 3

          назад 2

          назад 2

Выполнив эти три команды, Кузнечик переместится из точки 0 в точку –1. Выполнив программу еще раз из точки –1, Кузнечик переместится в точку –2. Так он сможет попасть в любую точку левой части числовой прямой.

Мы привели здесь эти рассуждения очень подробно, чтобы дать вам опору при обсуждении задачи с учениками. Задача эта необязательная и предлагать ее стоит только сильным детям, готовым к построению доказательства или по крайней мере готовым самостоятельно порассуждать, попробовать варианты, поискать частные решения. Конечно, сразу построить полное доказательство у детей не получится. Но в процессе обсуждения вы можете подтолкнуть ребенка на правильный путь, подсказать, как построить доказательство, не подсказывая, конечно, само решение.

Задача 186. Необязательная. Для начала стоит разобраться, как вообще должна выглядеть программа, которая вернет Кузнечика с такой системой команд в ту же точку, из которой он стартовал. В программе, которую мы составляем, будет несколько команд вперёд 4 и несколько команд назад 3. Так как Кузнечик вернется в ту точку, откуда начал, то сумма всех шагов, сделанных вправо в процессе выполнения этой программы, должна быть равна сумме всех шагов, сделанных влево. Таким образом нужно найти такое число, которое кратно и 4, и 3. Например, это может быть число 12 или число 24 и т. п. Возьмем число 12: при этого числа делении на 4 получается 3, значит в программе должно быть три команды вперёд 4. При делении числа 12 на 3 получается 4, значит, в нашей программе должно быть четыре команды назад 3. Итак, выполнив такую программу: Кузнечик вернется в ту же точку, откуда начал:

          вперёд 4

          вперёд 4

          вперёд 4

          вперёд 4

          назад 3

          назад 3

          назад 3

          назад 3  

В построенной нами программе оказалось как раз 7 команд, поэтому мы нашли решение.

На самом деле совершенно не обязательно команды в программе ставить именно в том порядке, который мы выбрали: их можно поставить в любом порядке! Любая программа, составленная из этого набора команд, будет годится в качестве решения. Этот факт совершенно не очевиден для ваших детей. Поэтому стоит его обсудить в классе или дать задание детям его проверить – составить такие программы и проверить.

Сильным детям можно дать дополнительное задание: составить программу, возвращающую Кузнечика в ту же точку, которая составлена из больше числа команд.

Задача 187. Необязательная. Довольно сложная задача, предназначенная в основном для ребят, которые любят рассуждать и не боятся необычных задач. Это известная математическая задача для олимпиадной работы с пятиклассниками. Посмотрим на нее с точки зрения нашего курса информатики.

В работе над этой задачи детям необходимо выделить из условия важную информацию, отделить ее от чисто сюжетной. Нужно представить себе, как разворачивалось само действие во времени. Для решения достаточно представить этот процесс в виде дискретного набора картинок-кадров.

Картинка 0 – начальный момент, Пятачок и Винни-Пух стартуют в противоположных направлениях, собираясь обойти вокруг озера.

Пятачок бежит в 3 раза быстрее, значит, он сделает полный круг первым. Будем рисовать картинки к каждому моменту, когда Пятачок попадает в стартовую точку – делает очередной полный круг.

Картинка 1 – момент, когда Пятачок 1 раз обошел озеро. На этой картинке важно правильно обозначить положение Винни-Пуха: он к этому моменту пробежал только треть берега озера. За время, прошедшее с момента Картинки 0, Винни-Пух и Пятачок встретились 1 раз (неважно, в каком месте берега озера). Действительно, встреча не могла не произойти, потому что Пятачок сделал полный круг, а Винни-Пух тоже бежал вокруг озера. Встреча не могла быть больше одного раза, потому что Пятачок за это время сделал только один круг.

Картинка 2 – момент, когда Пятачок завершил второй полный круг. Винни-Пух при этом всего пробежал две трети берега озера. За время, прошедшее с момента Картинки 1, они встретились только 1 раз.

Картинка 3 – момент, когда Пятачок завершил третий полный круг. Винни-Пух при этом тоже оказался в стартовой точке – значит, это момент их третьей встречи!

На следующих трех кругах все повторится точно так же – друзья встретятся еще три раза.

Заметьте, что решение получилось простым и «прозрачным», потому что мы выбрали правильный шаг – расстояние во времени между картинками у нас было одинаковым и ровно таким, чтобы на промежутке между двумя соседними картинками друзья встретились ровно один раз. Детям прийти к такому выбору будет не так уж просто. Наверняка они будут пытаться сначала рисовать моменты встречи, пытаясь прикинуть, в какой именно точке она произойдет. Но дайте им попытаться решить задачу самостоятельно. Стоит подсказать сам принцип, подход – фиксацию моментов и рисование картинки – условной схемы.

Ответ: друзья встретятся 6 раз.

Задача 188. На этом этапе эта задача будет нетрудной для большинства детей. Они уже освоились с Роботом, решили достаточно задач и в тетради, и в компьютере. Поэтому большинство быстро догадается, что надо заменить каждую команду в программе на противоположную. Напомните детям о необходимости проверки – пусть нарисуют путь Робота «туда» (выполнение заданной программы) и «обратно» (выполнение составленной программы) и сравнят результаты.

Задача 189. Необязательная. Для решения задачи достаточно посмотреть в календарь и найти там любой месяц с 31 днем, как в марте. В таком месяце пять раз повторяются три дня недели. Если известно, что четвергов было пять, а пятниц только четыре, это означает, что 31 марта было четвергом. Значит, 21 марта было понедельником.

Конечно, можно решить эту задачу и чисто математическими рассуждениями. В марте 31 день, при делении на 7 число 31 дает остаток 3. Это означает, что три дня недели встречаются по 5 раз (первая группа дней недели), а остальные четыре дня недели – по 4 раза (вторая группа дней недели). Условие задачи указывает, где проходит граница между этими днями недели: четверг был последним днем из первой группы, значит, четвергом был и последний день месяца. Дальше – просто: 31 число было четвергом, значит, четвергом же были 24 и 17 числа, а 21 число было понедельником.

Задача 190. Необязательная. Несложная задача на повторение. На уроке подготовки к контрольной работе ее можно предложить всем, за исключением наиболее сильных учащихся. На уроке выравнивания – тем, кто слабо справился с аналогичной задачей из контрольной работы.

Ответ: утверждение D не имеет смысла, утверждения А и Е – ложны, все остальные утверждения истинны.