Компьютерное дополнение к курсу Информатика 5. 2017

Уроки 19–21. «Члены последовательности. Когда утверждения не имеют смысла»

Ветвление времени, возможность выбора в истории всегда занимали философов и теологов. Если весь ход истории заранее записан в Книге или спланирован Господом, то что зависит от человека? Проблема эта неоднократно обыгрывалась и в научной фантастике. В частности, «эффект бабочки» (Рей Брэдбери) состоит в том, что выбор, случившийся в далеком прошлом и выглядевший там весьма незначительно (раздавленная бабочка), приводит к достаточно радикальным изменениям в истории цивилизации, грамматические правила и политические партии становятся иными.

В математике и информатике ветвящееся время и возможные миры – один из основных способов формального задания смысла логических высказываний в различных формальных языках. Это попытка отразить в формальных языках особенности естественных языков, в частности такие понятия, как «возможно», «необходимо», «вероятно», «когда-то», «желательно», «доказуемо». В другой ветви математики рассматриваются «теория катастроф» и «теория хаоса», также изучающие то, каким образом очень маленькие изменения и незначительные ветвления приводят к глобальным эффектам.

Этим применение формальных деревьев и их графических представлений в человеческой практике не ограничивается. Очень полезными оказываются деревья при классификации. Тогда ветвление соответствует выбору того или иного значения признака классификации. Например, можно классифицировать детей в школе по параллелям, внутри параллели по буквам (5А и 5Б), потом по алфавиту или как-то еще.

В современном компьютерном мире широко распространились деревья ссылок в составе так называемых гипертекстов. Однако деревья ссылок от одного слова к другому существуют и в обычных, бумажных энциклопедиях.

Языковые структуры тоже удобно представлять в виде деревьев.

Мы уже познакомили детей с двумя структурами – множеством и последовательностью. Множество – структура, лишенная порядка. Последовательность – структура с линейным порядком. Начиная разговор о последовательностях, мы упоминали о последовательности событий. Однако нам не всегда интересна простая линейная последовательность событий. Оглядываясь вокруг, изучая явления и объекты окружающего мира, мы видим, что есть и другие упорядоченные структуры, порядок элементов в которых не линейный.

Приведем несколько примеров:

– перед нами стоит возможность выбора и нам приходится рассмотреть несколько вариантов дальнейшего хода событий: «Направо пойдешь – коня потеряешь, налево пойдешь – буйну голову сложишь, прямо пойдешь – на царевне женишься»;

– мы выбираем один из возможных объектов, а потом хотим изменить свое решение и выбрать другой;

– мы выделяем в задаче подзадачи, раздаем их участникам, а потом собираем результаты и получаем одно общее решение.

Во всех этих случаях ситуация выбора, ветвления может повторяться, одним выбором дело не заканчивается. Например, в играх партнеры делают свой выбор много раз, на каждом ходу игры. Для графического представления таких процессов используется деревья.

В нашем курсе рассматриваются не все деревья, которые есть в современной математике и информатике, а только те, которые больше всего приближены к последовательностям. По сути, каждое наше дерево можно «разобрать» на совокупность последовательностей. В нашем курсе деревья обладают следующими фиксированными свойствами:

– в каждой вершине дерева у нас обязательно находится некоторый объект (бусина, буква, цифра, фигурка, множество) – в математике же рассматриваются и такие деревья, вершины которых не обязательно помечены (не обязательно в каждой вершине стоит какой-то объект);

– в нашем курсе элементов первого уровня в дереве может быть несколько – а в математике в основном используются только деревья с единственной вершиной первого уровня и эта вершина называется корнем дерева;

– наши деревья направлены, они «растут» в одну сторону (обычно сверху вниз): у каждого элемента, если он не является листом, может быть несколько следующих элементов и не больше одного предыдущего элемента (для элемента первого уровня – ни одного, для элементов других уровней – ровно один) – в математике рассматриваются как направленные деревья, так и ненаправленные деревья, для которых понятия следующий и предыдущий неприменимы.

Понятие уровень элемента в дереве не является, строго говоря, содержательным понятием нашего курса. Это, скорее, технический термин – как, скажем, понятия начала и конца последовательности. Введение понятия уровня элемента поможет ребятам при самостоятельной работе с деревьями. Мы в учебнике будем строить деревья по уровням, поэтому в наших деревьях детям всегда будет легко разобраться. Постепенно и дети будут учиться строить деревья по уровням. Это позволит красиво расположить дерево на странице и допустить меньше ошибок. Также использование понятия уровня элемента позволит нам сформулировать интересные задачи.

Дети, которые изучали наш курс в начальной школе, знакомы с понятием уровень дерева, теперь придется привыкать говорить уровень элемента. Впрочем, даже если дети будут говорить, как привыкли, это не страшно. Новым по сравнению с курсом начальной школы является понятие высота дерева. Оно является аналогом понятия длина последовательности, но в отличие от него не описывает полностью все количественные параметры дерева: у дерева есть еще общее число вершин, число вершин на каждом уровне и т. п.

Не смотря на то, что детям, которые изучали наш курс в начальной школе, материал большей частью будет знакомым, мы не советуем вам совсем пропускать этот параграф: круг задач, предлагаемых в этом параграфе, несколько отличается от тех, которые предлагались в курсе 3 класса. Классы, изучавшие наш курс в начальной школе, могут пройти эту тему не за три, а за 1 – 2 урока, при этом важно, чтобы учащиеся решили все обязательные задачи, аналогичных которым не встречалось в курсе начальной школы – такие задачи мы отметим в наших комментариях.

Полный перебор и деревья

Конструкция полного, исчерпывающего перебора важна в нашем курсе и вообще в жизни. Представьте себе на секунду поиски пропавшего паспорта в квартире или ровно «той самой» кофточки. В этой ситуации бывает нужно последовательно просмотреть все места, полки, ящики и т. п. Часто вещь находится «в самом неожиданном» месте, там, куда вы ее положили, «чтобы она не пропала». Надеемся, что в реальности вам не приходится заниматься такими поисками.

Иногда бывает очень нужно сократить перебор, придумать, где вещи точно не может быть и т. п. Но прежде чем изобретать разные стратегии сокращения перебора, нам следует понять, как организовать действительно полный перебор. Выписывание всех путей дерева является примером полного перебора.

С другой стороны, во многих случаях перебор естественно представить себе в виде перемещения по дереву. Например, в случае поисков в квартире можно соотнести со всей квартирой вершину первого уровня (если вы уверены, что вещь в квартире, что к сожалению, не всегда так: вы могли забыть ее на работе либо у знакомых или просто потерять на улице); следующие вершины – это комнаты квартиры, кухня и коридор; за комнатами идут шкафы, полки и столы, стоящие в комнатах; в шкафах есть отделения и полки и т. д.

Последовательность из дерева

Лист определений «Последовательность из дерева» связывает понятия дерево и последовательность. Действительно, любое дерево всегда можно «разобрать» на последовательности, то есть сопоставить дереву набор всех последовательностей из него. Заметим, что вообще говоря, в дереве могут быть и одинаковые последовательности. Поэтому набор последовательностей из дерева не всегда является множеством. В общем случае все последовательности дерева образуют мешок.

Родители и дети

Если подходить к нашей терминологии формально, то острой необходимости во введении понятий родители и дети нет, так как, по сути, они дублируют понятия следующий и предыдущий. Но, как вы скоро убедитесь, с помощью понятий родители и дети задачи можно сформулировать короче и проще. А явная договоренность о том, что элементы первого уровня не могут быть детьми, а листья – родителями, позволяет избежать в задачах дополнительных оговорок.

Есть и другая причина появления этих понятий в нашем курсе – для детей они очень естественны и создают в головах учащихся массу ассоциативных цепочек, которые позволяют повысить качество усвоения темы «Деревья» в целом. Несмотря на все эти очевидные преимущества, нам не хотелось отказываться от уже привычных детям терминов следующий и предыдущий, потому что они позволяют провести важные параллели между последовательностями и деревьями.

Задача 110. Все утверждения здесь содержат понятия «все/каждый». Проверка такого утверждения подразумевает полный перебор всех подходящих объектов. Однако организовать такой перебор на дереве оказывается сложнее, чем на последовательности: в последовательности можно просто двигаться по порядку от начала к концу. Поэтому можно посоветовать детям выбрать некоторую систему перебора. Например, можно двигаться по уровням от начала дерева вниз и на каждом уровне –слева направо.

Утверждение U. Чтобы не потерять листья, начинаем с верхнего (первого) уровня. На первом уровне мы находим не треугольный лист, значит, дальше перебор нет смысла продолжать – утверждение ложно.

Утверждение V. На первом уровне дерева есть один лист, он красный. Переходим на второй уровень, там есть два листа, они оба красные. Так будем двигаемся по уровням, пока не дойдем до последнего, четвертого, и не убедимся, что утверждение V истинно.

Ответ: истинные утверждения: V, W, X; ложные утверждения: Т (на первом уровне есть и квадратная бусина), U (в дереве есть и квадратные листья); утверждение Y не имеет смысла, поскольку перед красной квадратной бусиной первого уровня нет предыдущей.

Задача 111. В курсе начальной школы подобные задачи встречались. В числе прочего здесь есть утверждения, не имеющие смысла. Работу с ними надо продумать заранее, возможно, стоит обсудить такие утверждения всем классом. В любом случае при проведении общей проверки нужно попросить учеников не только читать значения истинности, но и объяснять свою точку зрения, особенно если утверждение ложно или не имеет смысла.

Ответ: Истинные утверждения: К, М, N, S. Ложные утверждения: L (предыдущая фигурка перед волком – бегемот), О (в дереве У 9 листьев), Q (белка – следующая фигурка после лошади). Утверждения, не имеющие смысла: Р (в дереве У нет кошки), R (в дереве У нет коровы).

Задача 112. Задача на построение всех последовательностей дерева. Напомните детям о необходимости использовать при решении таких задач метод полного перебора, чтобы не потерять последовательности и никакую не выписать дважды. Как сказано на листе определений, каждому листу дерева соответствует ровно одна последовательность – такая, последний член которой – этот лист. Поэтому для дерева можно всегда построить столько последовательностей, сколько в этом дереве листьев. Поэтому перебор путей нужно вести, перебирая листы дерева. Можно помечать в дереве лист, для  которого последовательность уже построена.

Мы поместили в эту задачу указание к проверке, чтобы постепенно прививать детям привычку сверять число построенных последовательностей с числом листьев в дереве. Вообще формирование умения проверять свое решение мы считаем одной из важных целей нашего курса. В случае, если для проведения проверки можно дать готовый алгоритм, мы всегда обращаем на это внимание детей.

Ответ: нарисованы 8 последовательностей – одна длины 1, две длины 2, три длины 3, две длины 4.

Задача 113. Скорее всего, ребята будут решать эту задачу методом проб и ошибок. В ходе этих проб ребята будут все ближе приближаться к решению, постепенно понимая, как устроено дерево. Пользуясь первым утверждением, выписываем буквы первого уровня – А и Б. Следующие за буквой А (если она не лист дерева) – две буквы Б, следующие за буквой Б (если она не лист дерева) – три буквы А. И так на следующих уровнях. Всего в дереве должно быть 12 букв. После того, как правила построения дерева прояснены, построить его не будет слишком сложным делом.

Несмотря на то, что деревья у ваших учеников получатся разными, все они могут быть описаны так: всех уровнях дерева, кроме первого, должны быть две тройки букв А и две пары букв Б, а все остальные буквы являются листьями.

Чтобы доказать единственность этого решения, порассуждаем. Всего в дереве должно быть 12 букв, из них на первом уровне 2 буквы, значит на остальных уровнях – 10 букв. Эти 10 букв составлены из пар букв Б и троек букв А. Попробуем представить 10 в виде суммы двоек и троек, получим ровно два таких разложения: 2+2+2+2+2 и 3+3+2+2. Построить дерево только из пар букв не получится – это означает, что все буквы Б должны быть листьями, но в таком случае в дереве будет только 4 буквы. Значит, годится только второе разложение: на втором и третьем и м. Б. Четвертом уровнях дерева должны быть две тройки букв (букв А) и две пары букв (букв Б).

Задача 114. Поскольку решения у ребят будут разные, можно устроить парную проверку, попросив ребят поменяться тетрадями и проверить решения друг друга. Перед парной проверкой нужно правильно сориентировать детей и обозначить, на что нужно обращать внимание:

проверить, правильно ли построено дерево: а) идет ли сверху вниз; б) помечен ли корень; в) соединены ли вершины; г) помечены ли листья.

проверить, правильно ли учащийся ответил на вопросы. Поскольку в задании мы не приводим образец ответа, то форма ответа может быть любой, в том числе правильным будет и односложный ответ – словесный или числовой.

Задача 115. Необязательная. Задача на повторение объединения и пересечения множеств. Не смотря на то, что множества в задаче уже даны, эта задача оказывается сложнее тех, где нужно просто выполнить операции объединения или пересечения. Причина в том, что здесь не известно, над какими множествами производились действия, это тоже нужно выяснять в ходе решения. Если при этом делать полный перебор, то задача окажется технически слишком сложной. Поэтому для начала есть смысл посмотреть на набор множеств и сделать некоторые предварительные выводы. Так для нас важно, что все множества здесь состоят либо из трех, либо из пяти элементов. Из этого можно сделать вывод, что объединяются множества из трех элементов, а пересекаются – из пяти. Например, найдем множество – пересечение двух трехэлементных множеств. Будем перебирать трехэлементные множества попарно, причем множества, не имеющие общих элементов можно отбрасывать сразу, ведь в их объединении будет не пять, а шесть букв. Перебор при этом оказывается не таким уж и большим. Получаем, что множество G7 – объединение множеств G5 и G 11. Аналогично переберем попарно все пятиэлементные множества и найдем искомое пересечение.

Задача 116. Задача скорее развлекательная – построить все последовательности дерева V совсем не сложно. Получится стихотворение:

Мистер и миссис Бокли ночью проснулись вдруг.

Мистер и миссис Бокли открыли старый сундук.

Мистер и миссис Бокли достали из сундука

Большие морские бинокли и орехов четыре мешка.

Можно эту задачу превратить в мини-проект: попросите детей поискать другие стихотворения, которые можно «собрать» в дерево – надо найти такие, в которых есть повторяющиеся начала строк. Это надо искать именно в стихах, потому что в прозе повторяющиеся начала предложений найти совсем затруднительно.

Задача 117. Необязательная. Сложная лингвистическая задача для сильных учеников.

Лингвистические задачи принадлежат к особому жанру. Впервые они появились на Олимпиаде по языковедению и математике, проводившейся филологическим факультетом МГУ с 1965 г. Задачи этих олимпиад называются «самодостаточными лингвистическими задачами». Это действительно именно задачи, а не просто упражнения, их нужно решать – ответ достигается в результате логических операций, а решивший задачу может (с известной степенью строгости) доказать правильность своего ответа. Самодостаточность такой задачи проявляется в том, что от решающего не требуется специальных знаний и подготовки: все необходимые ему данные содержатся в условии задачи. Кроме того, при решении ученик применяет свои интуитивные представления об устройстве родного языка.

Лингвистические задачи в нашем учебнике, конечно, являются лишь подготовительным материалом для работы над настоящими самодостаточными лингвистическими задачами. Тем не менее, несмотря на свою простоту, они обладают теми же свойствами: являются задачами и требуют интуиции и опыта в отношении родного (русского) языка.

Лингвистические задачи предназначены в основном для сильных и сообразительных детей, которые любят рассуждать. Для решения таких задач кроме обычной (формальной, математической) логики нужна некоторая языковая интуиция. На решение таких задач трудно навести и уж тем более разложить его «по полочкам». Поэтому если ребенок в такой совсем запутался и не сдвигается с мертвой точки даже с помощью ваших намеков на решение, то может иметь смысл оставить на время лингвистическую задачу и вернуться к ней дома или на другом уроке. Многие такие задачи допускают решение в несколько подходов.

Но вернемся к решению задачи 117. По аналогии с русским языком мы могли бы в качестве догадки выдвинуть гипотезу, что русские однокоренные слова и в венгерском языке похожи – имеют одинаковую начальную часть. Указание в задаче говорит нам, что это действительно так. Кроме того, оказывается, венгерские слова разделяются на группы по значению, и в отличие от русских слов, слова в каждой из этих групп чем-то похожи. Попробуем соединить эти две идеи.

В русских словах имеется группа из трех однокоренных слов. Аналогичную группу можно выделить в венгерских словах: словам ЯБЛОНЯ, ЯБЛОКО, ЯБЛОКИ соответствуют венгерские слова ALMÁK, ALMA, ALMAFA (какое именно слово к какому относится мы пока не знаем).

Разделим группы русских слов по значению: 3 слова обозначают дерево, 2 слова – плод, 1 – деревья, 1 – плоды. Попробуем найти эти группы в венгерских словах, выделяя в словах что-то общее (но при этом не корень, не начало слова). Видим, что некоторые слова заканчиваются одинаково, причем как раз 3 слова заканчиваются на «FA», 2 на – «АК» и по одному на «ТЕ» и «МА». Сопоставляя два полученных вывода, получаем, что

ALMAFA – ЯБЛОНЯ

АLMÁK – ЯБЛОКО

Значит,

ALMA – ЯБЛОКИ

Отсюда следует, что:

KÖRTE – БЕРЕЗЫ

Так постепенно двигаемся дальше, пока не находим полное соответствие русских и венгерских слов.

Ответ: NYÍRFA – ГРУША (дерево)

KÖRTE – БЕРЕЗЫ

АLMÁK – ЯБЛОКО

KÖRTEFA – БЕРЕЗА

NYÍRFÁK –  ГРУША (плод)

ALMA – ЯБЛОКИ

ALMAFA – ЯБЛОНЯ

Задача 118. Если детям приходится строить не произвольное дерево, а соответствующее некоторым условиям, то лучше всего вначале спроектировать его карандашом на черновике, а затем аккуратно нарисовать (и красиво разместить) в тетради. При проектировании дерева по мере проб и ошибок становится ясно, что раз шесть последовательностей из дерева имеют длину от 1 до 6, то на каждом уровне дерева должен находиться ровно один лист. Значит один из способов решения задачи – разместить на каждом уровне по одному листу-бусине и затем соединить их так, чтобы в результате получилось дерево. При этом можно дорисовывать только бусины, которые не являются листьями.

В этой задаче решений существует несколько. Дерево с наименьшим числом бусин будет содержать всего 11 бусин, на первых пяти уровнях по две бусины, на последнем – одну. Дерево с наибольшим числом бусин – дерево, для каждого листа которого придется вести свою отдельную последовательность, начиная от самого корня. В таком дереве будет 21 бусина.

Перед тем как дети начнут строить дерево в тетради, напомните им, что лучше строить дерево, располагая все вершины одного уровня на одной горизонтали. Для этого полезно провести предварительную разметку уровней – провести горизонтальные линии, отделяющие один уровень вершин от другого.

Задача 119. Несложная задача на повторение. Данную фигуру можно разбить на три части – два прямоугольных треугольника (1½  ед. кв. и 2 ед. кв.) и один прямоугольник (2 ед. кв.). Значит, площадь многоугольника Э равна 5, 5 ед. кв.

Задача 120. Здесь надо построить не все последовательности из дерева, а только последовательности длины 3. Перебор здесь также оказывается полезным. Рассмотрим все бусины третьего уровня (можно отделить третий уровень, приставив линейку). Теперь будем двигаться по этим бусинам как обычно слева направо. Как только находим следующий лист, выписываем «его» последовательность и помечаем лист. В результате оказывается три последовательности длины три. В ходе ответов на вопросы ребята закрепляют новую лексику, введенную на текущем листе определений. Кроме того, первые 4 вопроса парные, они позволяют сопоставить различные «древесные» понятия между собой. Можно устроить в этой задаче парную проверку, тогда в случае расхождений в ответах, дети смогут их обсудить и найти ошибку.

Ответы: а) 9; б) 9; в) 2; г) 4; д) 5; е) 3.

Задача 121. Несложная задача, поскольку дерево в ней строится не по описанию, а по инструкции. В данном случае дерево сильно зависит от того, какую бусину мы поставим на первый уровень. Например, мы выбрали красную круглую бусину. Все три бусины второго уровня должны быть разными и того же цвета, что и бусина первого уровня. Получим на втором уровне: красную треугольную, красную круглую, красную квадратную. Теперь рисуем после каждой бусины второго уровня по две бусины той же формы, что их родитель. Наконец раскрашиваем все бусины третьего уровня в разные цвета.

Задача 122. Не слишком сложная задача. Последнее условие является избыточным – если разрезать этот многоугольник на 4 одинаковых многоугольника, то их площадь в любом случае будет по 3 ед. кв. Поэтому в данном случае последнее условие играет роль дополнительной подсказки. Решений здесь существует несколько. Наиболее популярными, скорее всего, будут следующие: а) разрезание прямоугольника на 4 полосы по 3 клетки расположенные вертикально; б) разрезание прямоугольника на 4 фигурки из трех клеток, расположенных углом; в) разрезание прямоугольника вертикальной линией на два прямоугольника, а затем каждый из них на два треугольника по диагонали.

Задача 123. Задача среднего уровня сложности. Заметим, что в данном случае описание очень напоминает индуктивное и проще всего использовать его именно так. Поэтому, записываем первым членом последовательности число 13. Следующий (второй) член больше первого на 14, он равен 27. Затем находим третий член последовательности, добавляя ко второму 14 и так действуем до тех пор пока члены последовательности остаются меньше 100. Как только получаем член, который больше 100, останавливаемся, отбрасываем его и выписываем последовательность-ответ.

Ответ: 13 – 27 – 41 – 55 – 69 – 83 – 97.

Задача 124. Несмотря на необычность формулировки, задача эта оказывается не слишком сложной. Кроме того, здесь возможны различные решения. Основное ограничение достраивания каждого пункта – условие, чтобы соответствующие утверждения имели смысл. Конечно, инструкцию нужно выстраивать по порядку. При работе с первым пунктом мы можем использовать только форму бусин (ведь все бусины пока не раскрашенные). Треугольные бусины использовать нельзя, поскольку тогда для последней бусины цепочки первый пункт невозможно будет выполнить (соответствующее утверждение потеряет смысл). Треугольные и круглые бусины использовать можно. Тогда первый пункт может выглядеть так: «Раскрась следующую бусину после каждой круглой …..(цвет)», или так: «Раскрась следующую бусину после каждой квадратной…(цвет». При работе со вторым пунктом нельзя использовать ни круглые, ни квадратные бусины (иначе соответствующее утверждение потеряет смысл), но можно использовать треугольную форму. Тогда второй пункт будет выглядеть так «Раскрась вторую бусину перед каждой треугольной…(цвет)». Если после первого пункта оказались раскрашенными бусины не раньше третьей, то во втором пункте можно использовать и цвет. Третий пункт нужно достроить так, чтобы после него всего бусины оказались раскрашенными. Проще всего написать «Раскрась все остальные бусины…(цвет)».

Задача 125. Необязательная. В задаче используются буквы письма деванáгари.

Алфавит деванáгари – один из индийских алфавитов. Его древняя форма – нáгари – появилась в VII – VIII вв. Первые дошедшие до нас рукописи на нагари относятся к X – XI вв. Позднее письменность деванагари заняла центральное место среди алфавитов Северной Индии.

Сегодня деванагари употребляется для языков хинди, маратхи и других языков Северной Индии, а также для древнеиндийского языка санскрит, являющегося в Индии языком гуманитарных наук и религиозного культа.

Каждая буква деванагари (кроме букв, обозначающих гласные в начале слова) обозначает слог, состоящий либо из одного гласного, либо из согласного и гласного «а». Прочие гласные после согласного обозначаются приписываемыми к нему (сверху, снизу или по бокам) дополнительными значками. Таким образом, получается около 600 различных знаков.

Письмо деванагари создавалось для индийских языков, в которых есть много звуков, не существующих в русском языке; например, согласный в букве  (в транскрипции – ŋa) читается как английское ng; согласный в букве  (в транскрипции – jha) – как слитно произнесенные английское j и украинское г; есть и такие звуки, которым нет аналогов в языках Европы. В задаче мы использовали только те буквы, для чтения которых имеются близкие соответствия в русском. Вот как читаются некоторые буквы из задачи:

Технически задача может оказаться довольно сложной, потому что буквы письма деванагари наверняка не знакомы ребятам. Найти одинаковые буквы хаотичным просматриванием здесь найти довольно затруднительно – ребятам придется воспользоваться методом полного перебора. Как именно записать ответ – остается на выбор ребенка. Например, можно нарисовать одинаковые буквы в тетради. Поскольку в данной задаче буквы расположены строками, то можно указать одинаковые буквы номером строки и столбца.

Ответ: одинаковые буквы – седьмая в первой строке и третья в последней строке.

Задача 126. Как и в задаче 121, решений здесь будет много. Уже на первом уровне у нас есть выбор – сделать обе бусины родителями или сделать одну бусину родителем, а другую – листом. После бусины-родителя (или после обеих) мы рисуем две следующие бусины – круглые бусины (черную и белую). Они будут располагаться на втором уровне и здесь у нас снова есть выбор – сделать родителем одну или несколько бусин. Также будет происходить на третьем и на четвертом уровне. Если все листья нашего дерева будут располагаться только на последнем уровне, то число листьев (и последовательностей) будет максимальным – 32. Если, наоборот, на каждом уровне (кроме последнего) одна бусины будет листом, то число листьев (и последовательностей) будет минимальным – 6. Таким образом, подходящее дерево может быть и очень большим и совсем не большим.

Дерево, которое дети строят в этой задаче, очень знаменитое. Элементы в нем – объекты лишь двух видов, причем после каждого элемента, который не является листом, идет ровно два следующих. Такое дерево называется двоичным (или бинарным). Ясно, что черную или белую бусины можно заменить на А и Б или 1 и 0, суть от этого не меняется. Если в бинарном дереве все листья находятся только на последнем уровне, то оно называется полным бинарным деревом. В таком дереве все последовательности имеют одинаковую длину, равную высоте дерева. Полное бинарное дерево высоты 5 будет иметь ровно 32 последовательности.

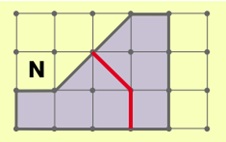
Задача 127. В этой задаче мы снова предлагаем детям найти площадь многоугольника на сетке, достроив его до подходящего многоугольника (см. комментарии к задаче 108). Если кто-то из детей невнимательно причитал условие и нашел площадь разрезанием, попросите его найти другой способ решения. Можно вернуть ребенка к решению задачи 108. Если задача 108 ребенком не решалась, порассуждайте вместе с ним. Видим, что многоугольник И получается, если отрезать от данного квадрата на сетке 5 на 5 клеток (25 ед. кв.) два треугольника: 2 на 3 клетки (3 ед. кв.) и 3 на 1 клетки (1,5 ед. кв.). Значит, площадь многоугольника И равна 20, 5 ед. кв.

Задача 128. Необязательная. Задача среднего уровня сложности. При ее решении необходимо помнить, что в множестве не может быть двух одинаковых бусин. Поэтому из утверждения «В этом множестве каждая треугольная бусина – красная» можно сделать следующие выводы: а) в данном множестве нет треугольных не красных бусин; б) в данном множестве есть ровно одна треугольная красная бусина. Аналогично можно сделать вывод о том, что в этом множестве ровно одна квадратная бусина и она синяя. Все остальные бусины данного множества должны быть круглыми и разными, значит, все они должны быть разных цветов. Таким образом, в этой задаче имеется ровно одно решение.

Задача 129. Необязательная. Как и во многих задачах на разрезание, здесь полезно сначала найти площадь многоугольника. В данном случае в многоугольнике имеется 7 целых клеток и две половинки – площадь равна 8 ед. кв., значит, площадь каждой части будет равна 8 ед. кв., при этом скорее всего одну из целых клеток при разрезании придется делить пополам. Остается найти эту клетку, в данном случае это можно сделать даже полным перебором.

Ответ:

Задача 130. Используются греческие строчные буквы.

Греческое письмо – алфавитное письмо, возникшее предположительно в VIII – VII вв. до н. э. В греческом письме в отличие, например, от древнееврейского, кроме букв, обозначающих согласные, появились буквы для передачи гласных звуков, что явилось новым этапом в развитии письма и сыграло важную общекультурную роль. Алфавитное греческое письмо разделялось на две ветви: восточногреческое и западногреческое. Восточногреческое развилось в классическое древнегреческое и византийское письмо и легло в основу коптского, готского и славянского кириллического, а также армянского и отчасти грузинского письма. Западногреческое письмо стало исходным для этрусского, латинского и древнегерманского рунического письма.

Население современной Греции говорит на новогреческом языке, в алфавите которого используются печатные литеры (начертания букв), созданные в XVII в. Направление письма – слева направо.

Вот греческий алфавит с современными русскими названиями букв:

Греческими буквами очень часто пользуются математики. Например, по традиции строчными греческими буквами обозначаются углы, буквами ε и δ – маленькие числа (в частности, маленькие изменения чисел). π – это длина окружности диаметром 1. Буквой λ в физике часто обозначается длина волны, есть обычай для математического употребления букв ι, υ, χ, σ, ω и др. Буква μ является обозначением единицы измерения длины – микрона, одной миллионной доли метра.

Ответ:

б)

в)

г)

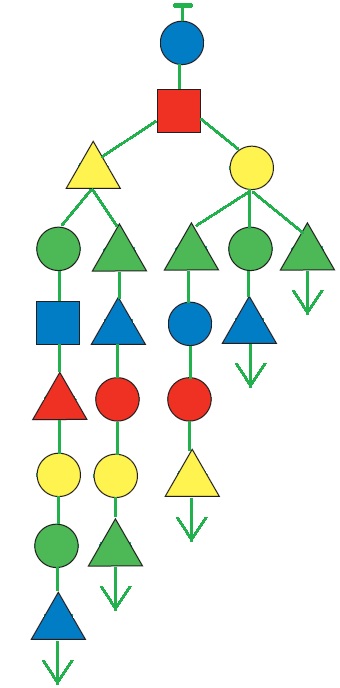
Задача 131. Условие задачи указывает на то, что задача имеет много решений. Действительно, дерево задается набором своих путей не однозначно. Причина в том, что на каждом уровне могут быть одинаковые бусины – бусины первого уровня или имеющие общего родителя. Если такие одинаковые бусины заменить на одну, то набор последовательностей не поменяется, а структура дерева (общее число элементов, число элементов на каждом уровне и т.д.) станет другой. Чаще всего дети стремятся построить по набору последовательностей дерево с минимальным числом вершин. В таком дереве не встречается одинаковых вершин, которые можно было бы «склеить». Однако по условию задачи этого не требуется. Верным будет и такое решение, где каждая последовательность выходит из собственной вершины первого уровня (такое дерево больше похоже на куст).

Ответ:

Задача 132. Аналогичная задача ребятам уже встречалась (см. комментарии к задаче 66). Как и в задаче 66, последовательность задана индуктивным описанием, и строить ее можно только одним способом – начиная с первого члена по порядку. При этом последовательность полностью определяется своим первым членом. Поэтому разных последовательностей по индуктивному описанию можно построить ровно столько, сколько можно взять разных первых членов последовательности. В данном случае таких будет две, одна из них будет последовательностью Ю, а другая – второй последовательностью, которую нужно построить в задаче.

Ответ: 1 – 6 – 11 – 16 – 21 – 26 – 31 – 36 – 41 – 46 – 51 – 56 – 61 – 66 – 71, 2 – 7 – 12 – 17 – 22 – 27 – 32 – 37 – 42 – 47 – 52 – 57 – 62 – 67 – 72.

Задача 133. Необязательная. Ключ к решению этой задачи в понимании того, что 12 рабочих сложат стену быстрее, чем 6, причем ровно в 2 раза. Если вы видите, что ребенок это не понимает, перейдите на доступные ему примеры, спросите, на что уйдет меньше времени – на дежурство в одиночку или с соседом и т.д.

Ответ: 12 рабочих сложат стену за 9 дней.

Задача 134. Находить площадь этого многоугольника достраиванием до прямоугольника оказывается несколько проще. Для этого достаточно из площади прямоугольника (5×3 ед. кв.) вычесть две площади прямоугольного треугольника (2×2 ед. кв.) и еще половину.

Ответ: площадь многоугольника А равна 10,5 ед. кв.

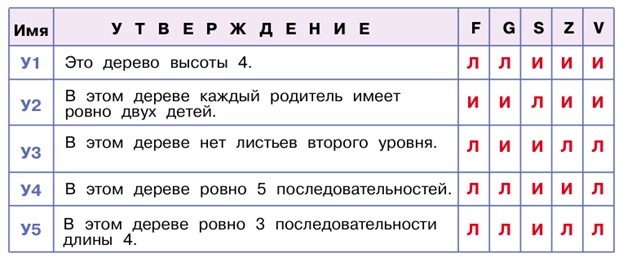
Задача 135. По существу это несложная задача на отработку лексики о деревьях. Технически задача усложнена тем, что таблица истинности относится сразу к пяти деревьям.

Ответ:

Задача 136. Необязательная. Очень интересная задача на сопоставление объекта и его описания. Мы умышленно дали описание в его оригинальном виде (гражданский шрифт, XIX в.), чтобы у ребенка была возможность почувствовать себя немного историком и лингвистом. Значение большинства слов в описании герба должно быть ребятам знакомо. Их оказывается вполне достаточно, чтобы найти нужный герб. С другой стороны, из этого описания, сопоставленного с картинкой герба, дети могут узнать новые слова и получить новые сведения: например, что означает слово «червленый» или как выглядит «Императорская корона» и «Андреевская лента».

Ответ: герб Казанской губернии – это фигурка 12.

Задача 137. Большинство ребят, скорее всего, нарисуют квадрат 3×3 и разрежут его пополам диагональю. Каждая из полученных частей будет представлять собой искомый треугольник. Однако здесь существует еще одно, менее популярное, решение – нарисовать прямоугольник 1×9 и разрезать его пополам диагональю.

Задача 138. Необязательная. Задача, предназначенная для сильных учеников. Дерево, которое получится в результате, – дерево разложения числа 900 на простые множители. Число 1 простым не является, поэтому элементы, равные единице, в нашем дереве запрещены. Разложим 900 на простые множители, получим 2×2×3×3×5×5. Эти шесть чисел и будут листьями нашего дерева. Но такие соображения детям, скорее всего, так сразу в голову не придут. Поэтому они начнут строить дерево методом проб и ошибок, как-нибудь: вершина первого уровня – число 900, его дети – числа, произведение которых равно 900. Возьмем, например, 9 и 100. Оба этих числа не могут быть листьями, иначе листьев будет только два, а не шесть, как требуется в условии. Так будем раскладывать родителей на множители и получать детей, до тех пор пока это будет возможно. Как только раскладывать станет нечего, листьев получится ровно 6. Таким образом, в этой задаче также существует много верных решений, но все подходящие деревья обладают общими свойствами: все листья – простые числа, все не-листья – составные числа. Число уровней подходящего дерева тоже может быть разным. Здесь мы приводим пример одного из самых коротких деревьев (высоты 3) и одного из самых длинных деревьев (высоты 6).

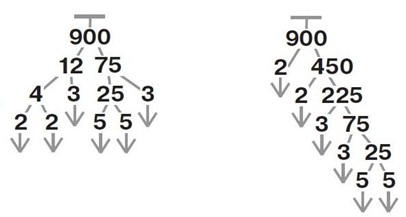
Задача 139. Необязательная. Математическая задача на логику и смекалку, скорее развлекательная, но при этом вполне относящаяся к теме «Последовательность». Здесь нам придется выстроить детей в последовательность длины 4 в соответствии с этажами дома. Здесь лексика «выше – ниже» аналогична употребляемой нами «раньше – позже» для последовательностей. Как и другие непростые задачи, ее лучше решать сначала на черновике карандашом, записывая имена  в последовательность не впритык, а так, чтобы между ними было легко вставить и другие имена. Например, Ваня живет выше Пети, значит, в нашей последовательности они идут как-то так:

…

Ваня

…

Петя

…

Но Ваня живет ниже Сени, значит, ставим Сеню после Вани, получается так:

…

Сеня

…

Ваня

…

Петя

…

Теперь осталось вставить в последовательность Васю:

Вася

Сеня

…

Ваня

…

Петя

Все четыре имени встали в последовательность – значит, пробелы можно удалить и соединить все четыре имени в последовательность.

Ответ: Петя живет на первом этаже, Ваня – на втором, Сеня – на третьем, Вася – на четвертом.

Задача 140. Сама задача по поиску двух одинаковых фигурок ребятам хорошо знакома, но объекты в этой задаче достаточно интересные и непростые – гербы губерний Российской империи XIX века. Если детям это покажется любопытным, поговорите немного о гербах. Как минимум, стоит убедиться, все ли дети понимают смысл слова «губерния», все ли знают, в какую губернию входил ваш город (село, деревня) в XIX веке. Если соответствующий герб есть среди данного набора, надо конечно показать его детям, по возможности объяснив смысл входящих в него элементов.

В задаче использованы следующие гербы:

Ответ: фигурки 6 и 24 одинаковые.