Компьютерное дополнение к курсу Информатика 5. 2017

Урок 4. «Одинаковые (равные) множества. Подмножество. Все разные»

Одинаковые (равные) множества

Множество полностью определяется набором элементов, которые лежат в этом множестве. Два множества оказываются одинаковыми, если для каждого элемента первого множества во втором найдётся такой же элемент, и наоборот, для каждого элемента второго множества в первом найдётся такой же элемент. Если хотя бы в одном из множеств есть один элемент, которого нет в другом множестве, то такие множества разные. Для записи равенства множеств мы будем использовать знак равенства, для записи неравенства – знак «не равно». 

Подмножество

Телесно проиллюстрировать понятие «подмножество» очень просто. Возьмем несколько разных деталей ЛЕГО и сложим их в кучку или в коробочку. Пусть это будет исходное множество А. Теперь любой набор деталей, который мы возьмем из этой кучки, будет представлять собой подмножество множества А. При этом мы можем забрать и сразу все детали, и не взять ни одной – это тоже будут подмножества множества А. Пустое множество является подмножеством любого множества. 

Мы решили не вводить в этом курсе обозначения действий над множествами, поскольку вопрос грамотного употребления математической символики – довольно сложная тема для обсуждения. Учебного времени в курсе не так много, достаточно, если дети освоят сами понятия. А усвоив понятия, дети быстро смогут освоить и обозначения – позже, в других курсах средней школы. Поэтому в задачах дети везде, где это нужно, будут использовать словесные формулировки, например: «А – это подмножество В».

Все разные

Это лист определений содержит необходимую нам общую договоренность, отсутствие которой может привести к неоднозначному пониманию формулировок задач. Дело в том, что понятие «одинаковые» употребляется нами в том же значении для двух элементов, что и для любого числа элементов, поэтому не требует никаких дополнительных договоренностей. С другой стороны, понятие «разные» мы определяем для двух объектов как отрицание одинаковости: «не одинаковые». С несколькими объектами простым отрицанием не обойтись: если среди трех объектов два одинаковых, а третий другой – то про эти три объекта уже нельзя сказать, что они одинаковые. Таким образом, «не одинаковые» и «все разные» для нескольких объектов не одно и то же. Бывает важно выделить именно тот случай, когда среди нескольких объектов нет ни одной пары одинаковых. Чтобы каждый раз не писать так длинно, мы и договариваемся писать в таком случае «все разные», выражение «четыре разных множества» все дети будут понимать одинаково. 

Для тех детей, кто изучал информатику в начальной школе, этот материал является повторением.

Задача 25. Простая задача на понимание материала листа определений. Множество Щ имеет 8 разных подмножеств: 3 одноэлементных, 3 двухэлементных, 1 трехэлементное и 1 пустое. Для решения достаточно указать любые четыре подмножества, поэтому возможных решений здесь много.

Задача 26. Ответ: 

а) возможных вариантов много; 

б) множество из трех красных бусины – всех трех форм; 

в) множество из 4 треугольных бусин – красной, синей, желтой и зеленой; 

г) пустое множество. 

Задача 27. Необязательная. Здесь необходимо внимательное чтение условия. Задания в пунктах а) и б) похожи, но понятие «все» относится в них к разным множествам. В первом случае мы должны сделать полный перебор букв алфавита и выделить из него все буквы, которые являются гласными – получится множество из 10 гласных букв. Таким образом, в первом задании существует только одно решение (Г={ А, Е, Ё, И, О, У, Ы, Э, Ю, Я}). Во втором случае понятие все относится не к буквам алфавита, а к буквам искомого множества. То есть все буквы множества Д должны быть гласными. Поэтому множество Д может состоять даже из одной гласной буквы, например, буквы А. Интересно, догадается ли кто-то из детей, что решение пункта б) всегда будет подмножеством решения пункта а)? В качестве решения пункта б) подойдет даже пустое множество – важно, чтобы букв в множестве В было меньше, чем в множестве Г. Иначе не получится сделать эти множества разными. 

Задача 28. Как и при поиске одинаковых фигурок, для решения этой задачи может помочь систематический перебор. Можно следовать такому правилу: берем первое по порядку множество, множество А, и сравниваем его со всеми остальными множествами. Если равного множеству А не находится, берем множество Б и сравниваем его со всеми оставшимися (не считая А) и т. д. Можно перебор проводить по элементам множеств. Во всех множествах по 4 элемента и один из них – лампочка. Остальные элементы есть не во всех множествах. Например, чашка есть лишь в 4 множествах (А, Г, З, И), а в остальных ее нет. Поэтому ясно, что множества из первой группы (А, Г, З, И) нет смысла сравнивать с множествами второй группы. Таким образом, задача разделилась на две подзадачи. Сравниваем множества первой группы – двух одинаковых среди них нет. Сравниваем множества второй группы (множества, в которых нет чашки). В каждом из них есть лампочка, ложка и ножик. Значит, чтобы найти одинаковые множества, остается только сравнить оставшиеся предметы.

Ответ: В = Ж.

Задача 29. Ответ: 

а) это подмножество совпадает с множеством И;  

б) это множество из букв А, В, Е, М, Н, Р, С, Т;  

в) пустое множество.

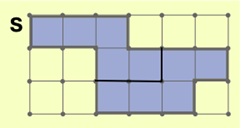
Задача 30. Необязательная. Это первая непростая задача на разрезание, поэтому ребятам может понадобиться ваша помощь. Оказать помощь в задачах на разрезание бывает не просто, поскольку при их решении большую роль играет геометрическая интуиция. Однако есть несколько простых соображений, которые часто работают в таких задачах. Первое – сосчитать число клеток в исходной фигуре и в будущих частях. В данном случае в фигуре S 10 ед. кв., значит, в каждой из двух равных частей будет по 5 ед. кв. Второе – часто в задачах на разрезание можно использовать метод перебора, если принять во внимание несложные геометрические соображения. Так, в данном случае из геометрических соображений можно сделать вывод, что три верхние клетки фигуры S и первая клетка второго ряда, скорее всего, принадлежат одной из частей. Это становится ясно, как только мы пытаемся сделать разрез в пределах этих клеток. Любой такой разрез полностью отделяет от фигуры часть, в которой меньше 5 клеток. Осталось присоединить к этим 4 клеткам еще одну, перебор при этом получается совсем небольшой, и сразу находим правильный ответ. 

Ответ:

Задача 31. Данная задача полезна для закрепления понятия «подмножество». В ней впервые встречается формулировка «выдели подмножество». Кроме того, для решения этой задачи необходимо понимание отношения включения различных множеств четырехугольников: того, что прямоугольник является также и четырехугольником, а квадрат является прямоугольником и четырехугольником. В сильном классе полезно подытожить решение этой задачи общим обсуждением, в ходе которого прозвучит, что множество квадратов – подмножество множества прямоугольников, а множество прямоугольников – подмножество множества четырехугольников.

Ответ: 

б) 

в) 

г) 

Задача 32. Эта задача, конечно, гораздо сложнее, чем задача 25. Поскольку множество А имеет всего 8 подмножеств, 6 из них даны, то чтобы найти оставшиеся два, придется все-таки сделать перебор всех подмножеств. В множестве А 3 элемента, поэтому во каждом его подмножестве может быть не больше трех элементов. 

Одно трехэлементное множество – это данное подмножество В. 

Двухэлементные подмножества получаются, если вынуть из множества А один элемент. Вынуть можно любой из трех элементов, значит, двухэлементных множеств должно быть 3. В задаче даны два из них (С и D), значит, мы можем построить третье. 

Одноэлементных подмножеств тоже 3 – по числу элементов в множестве А. Но они все даны в условии (E, F, G). 

Кроме того, подмножеством любого множества является пустое множество – его мы и должны построить.

Ответ:

Задача 33. Необязательная. Для решения этой задачи необходимы простейшие знания о календаре. В нашей задаче речь идет о феврале, в котором может быть либо 28, либо 29 дней. Если в феврале 28 дней, то всех дней недели в этом месяце будет ровно по 4, в том числе в нем будет 4 воскресенья. По условию задачи в этом феврале было 5 воскресений, значит, в феврале того года было 29 дней и 29-е число и было как раз воскресеньем. Теперь совсем несложно выяснить, каким днем недели было 23 февраля.

Ответ: 23 февраля было понедельником.

Задача 34. Ответ: фигурки D, Q и V – одинаковые. Знак «Движение прямо или направо» (нельзя поворачивать налево и разворачиваться).