Информатика. 3–4 класс (часть 3) Демо+методичка

Уроки 21 – 22. «Дерево выполнения программ»

Дерево помогает нам в тех случаях, когда необходимо осуществить перебор всех возможных ситуаций, особенно если на каждом новом шаге нам опять предстоит выбор. Удержать все возникающие ветвления в голове подчас оказывается затруднительно даже взрослому, а ребенку и подавно. Дерево же дает простую и понятную модель, отражающую сразу все варианты возможного развития событий от первого до последнего шага.

На данном листе определений речь пойдет о дереве возможностей выполнения программы Робиком. Часто Робик может выполнить все четыре команды из той клетки, где он находится. Единственное, что его ограничивает – это стены, внутренние и внешние. Ясно, что Робик может выполнить команду лишь в том случае, если на пути нет стены. Если учесть, что ветвления (варианты выбора) есть и на первом, и на втором, и на третьем (и т. д.) шагах, то возникает множество вариантов возможных путей Робика. Соответственно существует множество программ заданной длины, которые Робик может выполнить из данного начального положения. Учесть все варианты поможет дерево. В качестве вершин дерева мы берем не сами команды, а результаты их выполнения – получившиеся позиции.

Итак, цепочка позиций – это способ представить динамический процесс в виде статичной последовательности моментальных снимков. Дерево позиций – это способ фиксировать различные варианты развития событий.

Понятие дерево выполнения программ, как и другие понятия, относящиеся к командам и процессам их выполнения, мы даем только на примере Робика и его фиксированной системы команд. Ясно, что эти понятия можно использовать и в более общей ситуации для любых исполнителей и систем команд. 

Решение задач из учебника

Задача 117. Здесь пока не требуется построения дерева выполнения программ, а нужно лишь поработать с уже построенным деревом У, но даже это может оказаться не простой задачей, ведь дерево У достаточно большое. В условии задачи мы специально обратили внимание ребят на стены, которые ограничивают передвижения Робика по полю. Если вы хотите до выполнения задания убедиться, что ребята понимают принцип построения дерева У, задайте им после знакомства с условием задачи несколько вопросов:

1. Почему дерево У имеет 5 уровней?

2. Почему вершина первого уровня имеет две следующие?

3. Почему самая нижняя вершина третьего уровня имеет одну следующую?

4. Почему не во всех листьях дерева число закрашенных  клеток одинаково? И т. п.

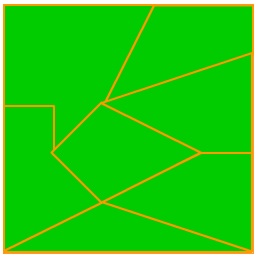
При выполнении первой части задания ребятам придется сопоставлять программы с путями дерева. Для того чтобы обвести в дереве некоторый путь, надо обвести каждую вершину этого пути начиная с позиции первого уровня и до соответствующего листа. Надеемся, ребят не смутит, что одна из вершин второго уровня в результате выполнения первого задания будет обведена дважды, а позиция первого уровня – трижды (см. рисунок).

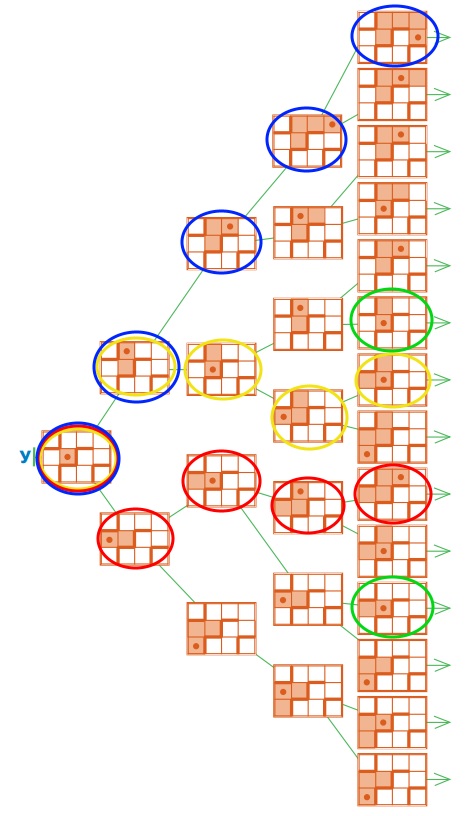
Если ребята понимают, как построено дерево У, то написание программы Г их не затруднит, ведь из позиции первого уровня Робик может выполнить лишь одну из двух команд – вверх или влево. Вторую команду конструкции повторения можно найти перебором по дереву. Например, в первое окно мы вписали вверх. Далее Робик может выполнить команды вправо или вниз. Пробуем выполнить каждую из получившихся программ Г и убеждаемся, что на данном поле выполнима лишь одна из них:

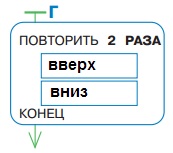
Если в первом окне записать команду влево, то получаем также лишь одну возможную программу Г:

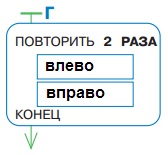
Задача 118. Ребята, разобравшиеся в листе определений, такую задачу решат без труда. Если у кого-то из учеников возникнет заминка, то побеседуйте с ним о возможностях выполнения команд Робиком. Понятно, что если Робик стоит на безграничном поле, то он в любой момент может выполнить любую из своих четырех команд. Но нам дано поле, внутри которого находятся стены. Поэтому первый ваш наводящий вопрос может быть таким: «Какие команды может выполнить Робик из начальной позиции?» Оказывается, что лишь одну – вниз, ведь в начальной позиции с трех сторон от Робика – стены. Значит, после позиции первого уровня следует лишь одна позиция. Далее можно спросить: "Какие команды может выполнить Робик из клетки, в которую он переместился?" Их три: вправо, вниз и вверх, ведь стена теперь лишь слева. Рисуем возможные позиции. Теперь для каждой из трех позиций проводим аналогичные рассуждения. Получаем следующее дерево Ш (см. рисунок).

Задача 119. Необязательная. Ребятам уже не раз приходилось решать задачи о двумерной таблице для мешка, но эта задача повышенного уровня сложности. Действительно, грузинские буквы для ребят не более чем закорючки, их невозможно держать в голове в виде общих понятий (например, «раскрашиваем красным три буквы Ю»), поэтому при раскрашивании буквы из мешка постоянно приходится сличать с образцом из таблицы. Решать такую задачу без системы довольно сложно. Например, можно раскрашивать буквы по строкам (или по столбцам) таблицы. Полезно сразу помечать в таблице ту клетку, которую уже использовали. Берем первую клетку первого столбца таблицы – в ней стоит число 0; значит, в мешке нет таких синих букв. Помечаем первую клетку и переходим ко второй клетке первого столбца. В ней стоит число 2, значит, в мешке должно быть две такие красные буквы. Находим  по образцу две любые такие буквы, раскрашиваем их красным, помечаем вторую клетку и переходим к следующей. Так можно продолжать работу до тех пор, пока все клетки в таблице на будут помечены.

Задача способствует тренировке наблюдательности и умения работать с малознакомой системой символов; кроме того дети еще раз увидят письменность наших соседей. Как называются и читаются грузинские буквы, вы можете посмотреть в книге для учителя к первой части курса («Информатика 3»).

Задача 120. Аналогичные задачи о выполнении операции разбиения, обратной склеиванию мешков цепочек цифр, ребятам уже встречались (см. комментарии к задачам 73, 85). В данном случае в мешке-результате должны лежать все двузначные числа. Все такие числа имеют ровно два разряда. В разряде единиц может стоять любая цифра, а в разряде десятков – любая цифра кроме 0. Это и определяет состав мешков А и Б.

Задача 121. Здесь ребятам снова предстоит анализировать дерево выполнения программы. Оба задания данной задачи удобнее всего выполнять, начиная с листьев. Например, выполняя первое задание, сначала можно пометить все подходящие листья (где Робик заканчивает выполнение программы в левом нижнем углу), таких оказывается 4. Затем следует обвести синим все пути, ведущие в эти листья (общую вершину для нескольких путей, например вершину первого уровня, достаточно обвести один раз), затем выбрать один путь и записать соответствующую ему программу Робика в первое окно. Возможные программы А:

Видим, что последняя программа подходит и под условие второго задания, поэтому путь, соответствующий ей, будет обведен дважды – синим и красным.

Задача 122. В данной задаче нужно установить соответствие между арифметическими выражениями и деревьями. Для того чтобы ребятам обязательно пришлось анализировать древесную структуру, все примеры составлены из одних и тех же чисел. Здесь не нужно анализировать все дерево полностью, чтобы найти подходящий для него пример. Возьмем, например, дерево А. Последнее действие, выполняемое для нахождения вершины первого уровня, – умножение. Видим, что пример, в котором последним выполняется умножение, один (последний); соединяем пример и дерево А его вычисления. При поиске соответствия для остальных выражений можно руководствоваться, например, первым действием. В дереве В первое выполняемое действие – деление 20 на 10, находим подобный пример и соединяем его с деревом В. Так мы продолжаем до тех пор, пока все примеры не будут соединены со своими деревьями. После этого задача становится привычной для ребят.

Возможно, найдутся дети, которые будут действовать при решении этой задачи совершенно по-другому: сначала заполнят все цветные окна в дереве (в том числе и в корневых вершинах), затем найдут значение каждого из выражений, наконец, соединят деревья с выражениями, руководствуясь одинаковыми числами в окнах примеров и корневых вершинах деревьев.

Ответ: 

А – 2 • (30 – 20 : 10 + 15) = 86

В – 2 • (30 – 20 : 10) + 15 = 71

С – 2 • (30 – 20) : 10 + 15 = 17

D – 2 • 30 – 20 : 10 + 15 = 73

Задача 123. Здесь ребята повторяют понятия перед каждой и после каждой. Пробы с бусинами с листа вырезания будут осложняться тем, что для некоторых бусин известен только цвет, а для некоторых известна только форма. Поэтому пробы можно осуществлять на листочке (или в окне карандашом), изображая пустую форму (квадрат, треугольник или круг) или цвет первой буквой (К, Ж, С, З). Решений у этой задачи, конечно, много, однако анализ утверждений позволяет выделить у всех подходящих цепочек следующие общие черты. Во-первых, в цепочке Ю должна быть хотя бы одна треугольная бусина, иначе второе утверждение не будет иметь смысла. Более того, в цепочке Ю должен содержаться хотя бы один отрезок «красная круглая – … – треугольная». Если использовать первое утверждение, то этот отрезок должен выглядеть так: «красная круглая – квадратная (не красная) – треугольная». Во-вторых, треугольных бусин в цепочке Ю не может быть больше двух, иначе в цепочке Ю будет и больше двух круглых, что противоречит последнему утверждению. Теперь остается проследить, чтобы в цепочке было 4 красные бусины и чтобы после каждой из них стояла квадратная.

Ясно, что самая короткая цепочка, удовлетворяющая условию, – цепочка длины 7, ведь в цепочке Ю, как говорилось выше, не меньше одной треугольной бусины, ровно две круглые и не меньше четырех квадратных (так как после каждой красной бусины должна стоять квадратная). Например, условию удовлетворяет цепочка: 

Однако цепочка Ю может быть и гораздо длиннее, поскольку число квадратных не красных бусин может быть любым. Например, нам подходит следующая цепочка длины 9: 

Задача 124. Необязательная. Задача потребует от детей внимания, сосредоточенности и, конечно, знания правила словарного порядка слов. Ребята сразу заметят, что первая буква у всех слов – С, а вторая – О. Теперь ничего не остается, как упорядочивать слова по третьей букве, т. е. сначала искать все слова, у которых на третьем месте буква А, далее буква Б, потом буква В и т. д. Облегчает выполнение задания то, что в мешке есть лишь два слова, в которых третьи буквы одинаковые: СОН и СОНЯ. Возможно, кому-то из ребят придется напомнить, что в подобных случаях раньше должно идти то слово, у которого четвертой буквы вообще нет (СОН). При расстановке столь большого числа слов в словарном порядке возможны ошибки, которые трудно будет потом исправить, если учащиеся сразу напишут слова ручкой, поэтому лучше писать слова в цепочку сначала карандашом. Кроме того, слова, уже записанные в цепочку, можно вычеркивать из мешка.

Ответ:

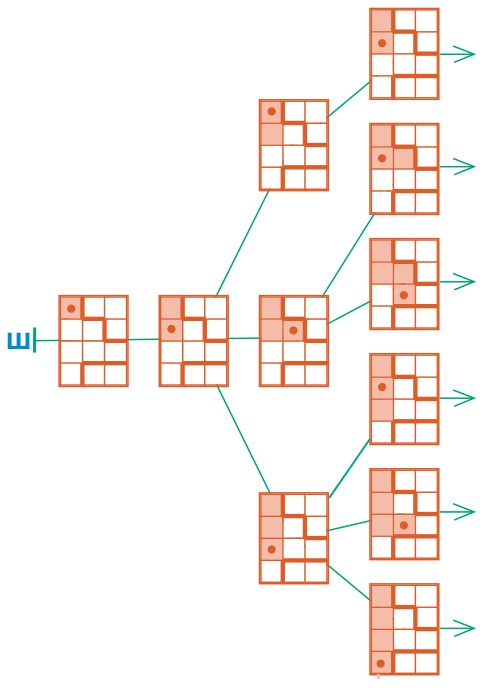
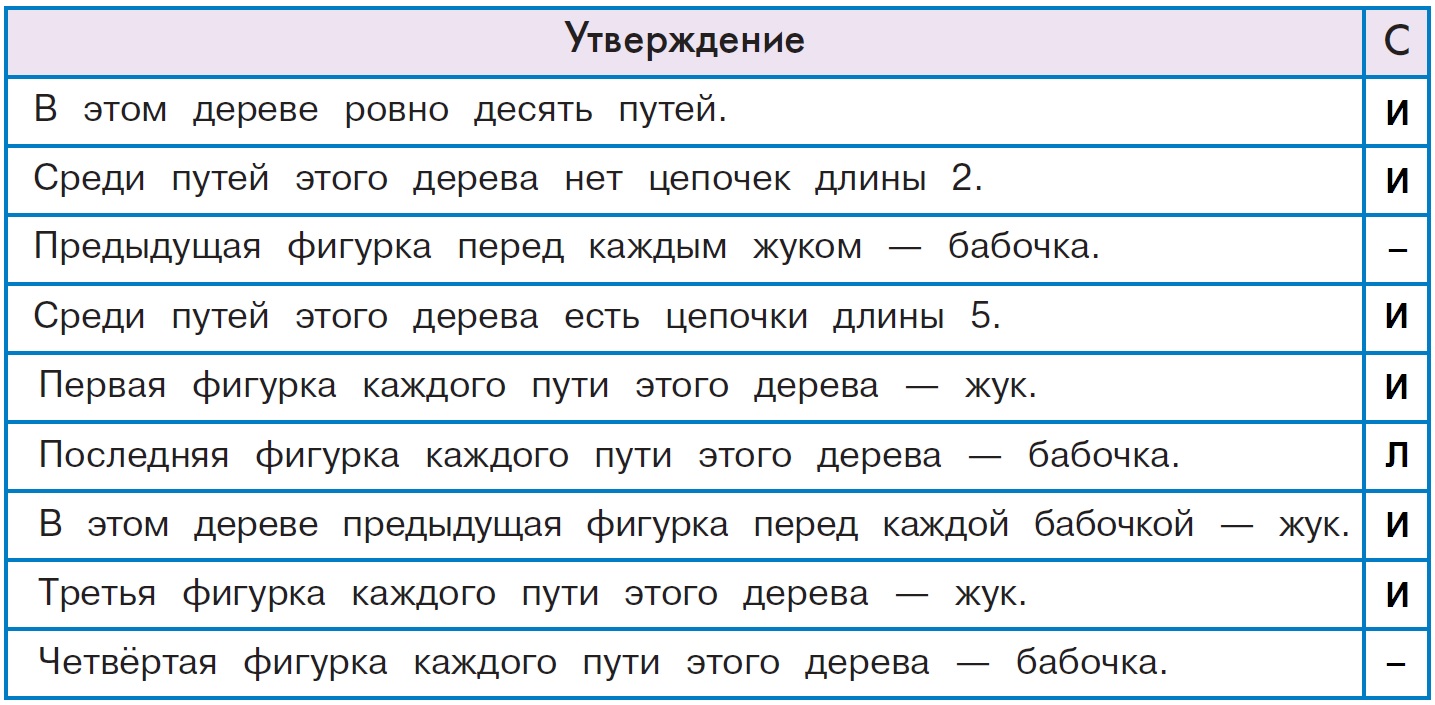
Задача 125. В этой задаче задействован довольно широкий круг понятий нашего курса. Особенно активно ребятам приходится работать с понятием путь, анализируя пути как цепочки с одной стороны, и как части дерева – с другой. Так, определяя истинность пятого утверждения, ребята должны понимать, что первая фигурка каждого пути – вершина первого уровня дерева. Поскольку в дереве С вершина первого уровня одна и эта фигурка – жук, то утверждение истинно. Чтобы определить истинность восьмого утверждения, нужно аккуратно перебрать все пути дерева, найти в каждой из цепочек третью фигурку (собственно, это все вершины третьего уровня) и проверить, что все эти фигурки –  жуки. Особого внимания заслуживают утверждения, не имеющие смысла для данного дерева. Третье утверждение не имеет смысла, так как вершина первого уровня – фигурка жука, и она не имеет предыдущей, а последнее – так как в дереве С есть пути длины 3 и в них отсутствует четвертая фигурка.

Ответ: 

Задача 126. Аналогичные задачи о склеивании цепочек, пограничные с курсом русского языка, ребятам уже встречались (см. комментарии к задачам 20 и  80). Как и в задаче 80, здесь для решения задачи ребенку необходимы некоторые знания из курса русского языка, поэтому данная задача хорошо подходит для интегрированного урока.

Компьютерный урок «Дерево выполнения программ», часть 1, задачи 112 – 118

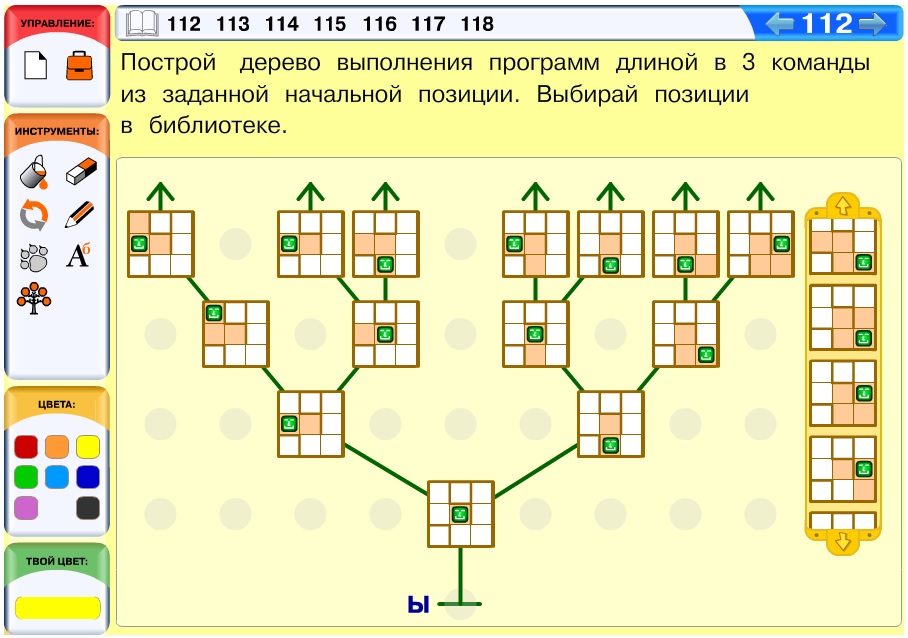
Задача 112. Задача о построении дерева выполнения программ, аналогичная задаче 118 из учебника. Однако компьютерные возможности позволяют решать подобные задачи быстрее: брать позиции из библиотеки гораздо легче, чем вырезать, наклеивать и раскрашивать. При этом содержательно данная задача не проще задачи 118. Мы умышленно дали в библиотеке позиции с избытком – среди них много неподходящих позиций. Чтобы выделить нужные позиции, ребятам необходимо разбираться по существу.

Вариант решения: 

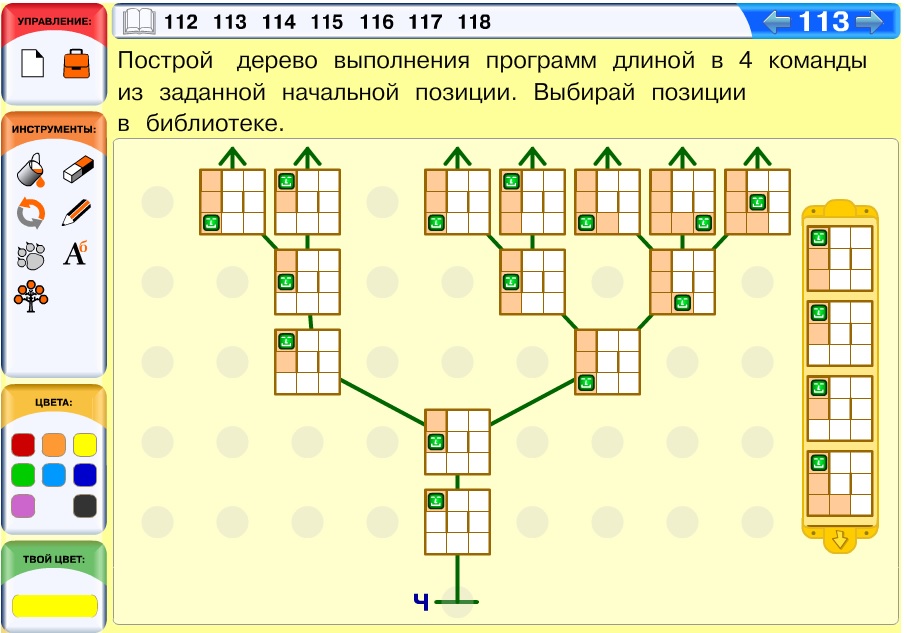
Задача 113. Задача, аналогичная предыдущей задаче этого курса.

Вариант решения:

Задача 114. Задача, аналогичная задаче 101 этого курса. В дереве здесь будет 5 уровней.

Вариант решения:

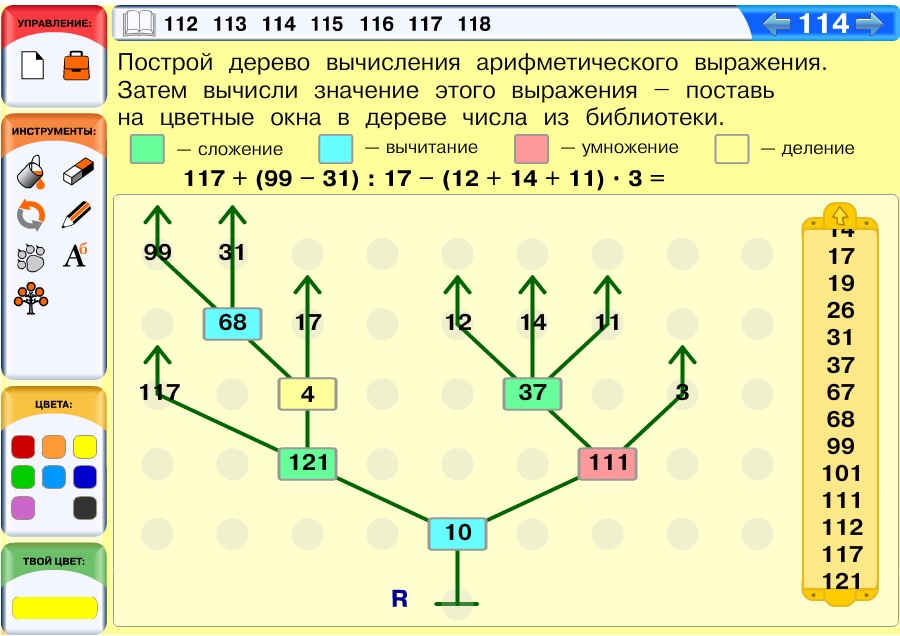
Задача 115. Задача, по структуре сходная с задачей 93 этого курса. Только здесь нужно достроить не дерево игры крестики-нолики, а дерево выполнения программ. Так как структура дерева уже задана, прежде чем раскрашивать поля, нужно предварительно проанализировать его структуру. На втором уровне позиции Робика определяются однозначно (ветки после этих позиций одинаковые). А на третьем уровне позиции нужно внимательно рассмотреть, так как из двух позиций третьего уровня на четвёртый уровень идут по две позиции, а из других двух – по одной. Если это сразу учесть, то дальнейшее построение не должно вызвать особых затруднений.

Вариант решения:

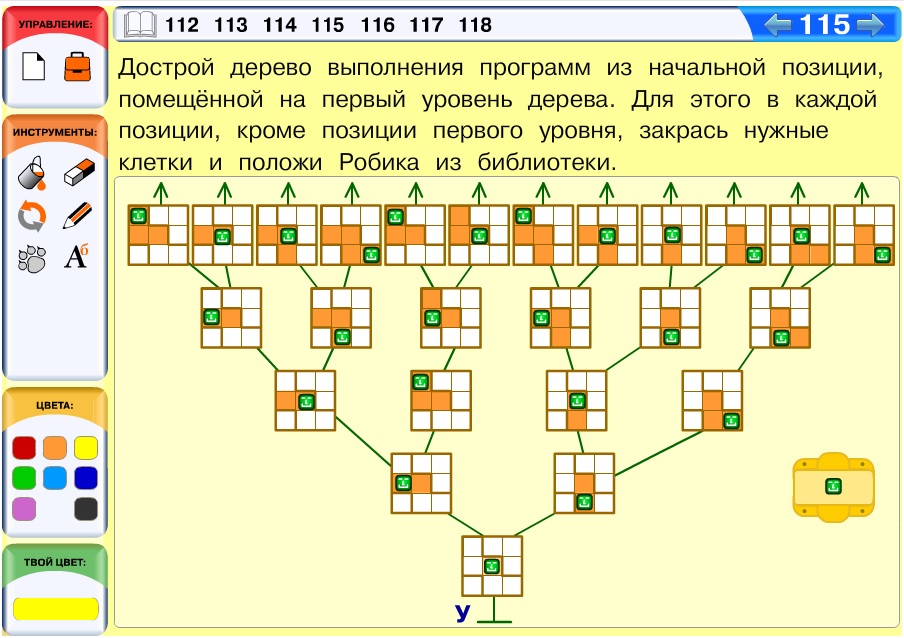
Задача 116. Задача о формулировании выигрышной стратегии в виде общего правила. Сначала нужно раскрасить числовую линейку: синим выделяем проигрышные позиции, а красным – выигрышные.

По числовой линейке видно, что чередование повторяется на каждых 11 позициях. Позиции 11n (числа, кратные 11), 11n+2 и 11n+4 будут проигрышными, остальные – выигрышными. В частности, позиция 23 – выигрышная, значит, выигрышную стратегию в игре с заданными правилами будет иметь Первый. Позиция 24 – проигрышная, а значит, выигрышную стратегию в игре из этой позиции будет иметь Второй.

Ответ:

Кто из игроков имеет выигрышную стратегию в игре с такими правилами и начальной позицией 23 камешка?  ПЕРВЫЙ.

Кто из игроков имеет выигрышную стратегию в игре с такими правилами и начальной позицией 24 камешка?  ВТОРОЙ.

Задача 117. Трудность данной задачи состоит в ограничении количества букв в дереве – их должно быть не больше 21 (меньше и не получится). Поэтому буквы придётся «экономить». Для этого сначала нужно сгруппировать слова по одинаковому началу: 

ЩУП	ЩИ	ЩЕКА
ЩУКА	ЩИТОК	ЩЕПА
ЩУЧКА	ЩИТ	ЩЕПКА

После этого можно приступать к построению дерева, помня о том, что одна буква не может быть одновременно и листом, и не листом.

Вариант решения:

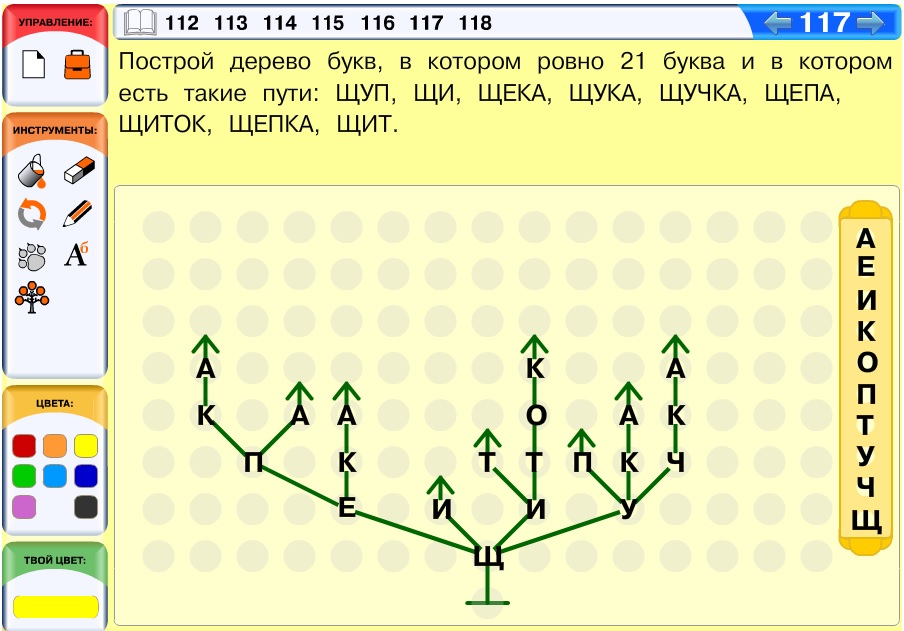
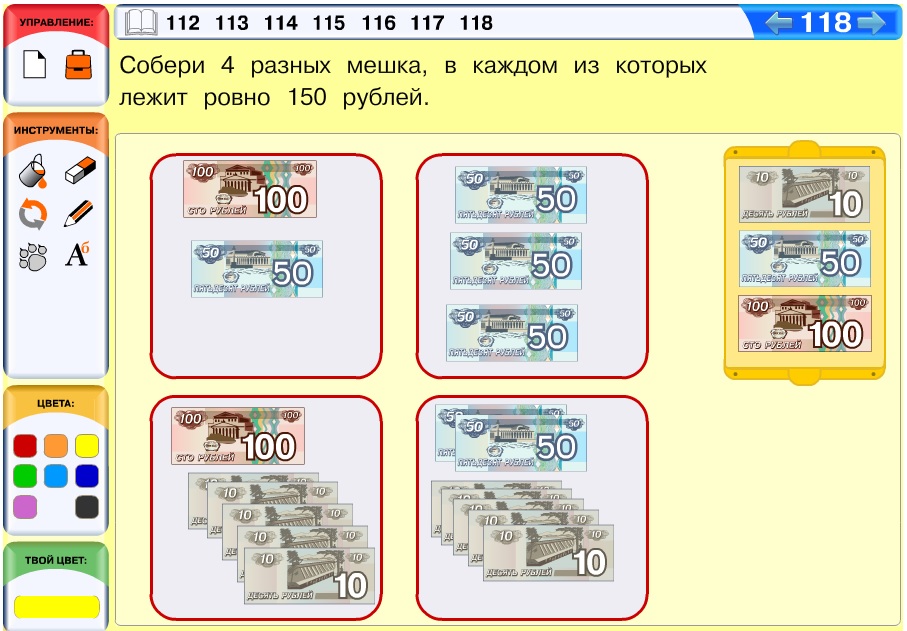
Задача 118. Задача более похожа на математическую и является в этом курсе скорее развлекательной. Вариантов решения может быть много. 

Вариант решения:

Компьютерный урок «Дерево выполнения программ», часть 2, задачи 119 – 125

Задача 119. Задача о построении дерева выполнения программ. Похожие задачи ребятам уже встречались (см. комментарии к задачам 112 и 113 этого курса).

Вариант решения:

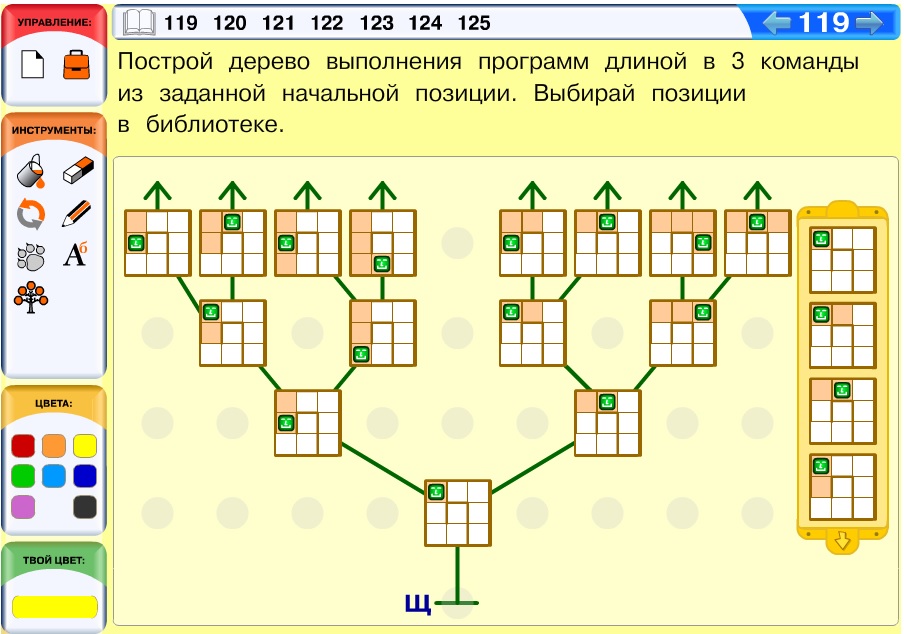
Задача 120. Задача о построении дерева выполнения программ, аналогичная задаче 115 этого курса.

Вариант решения:

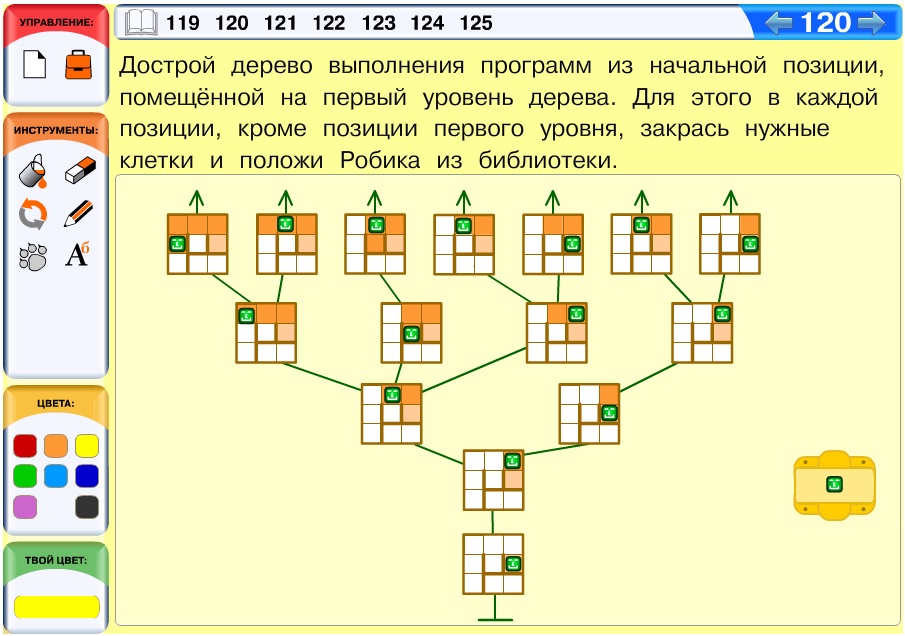
Задача 121. Как и в задаче 114 этого курса, в дереве вычисления здесь будет 5 уровней.

Вариант решения:

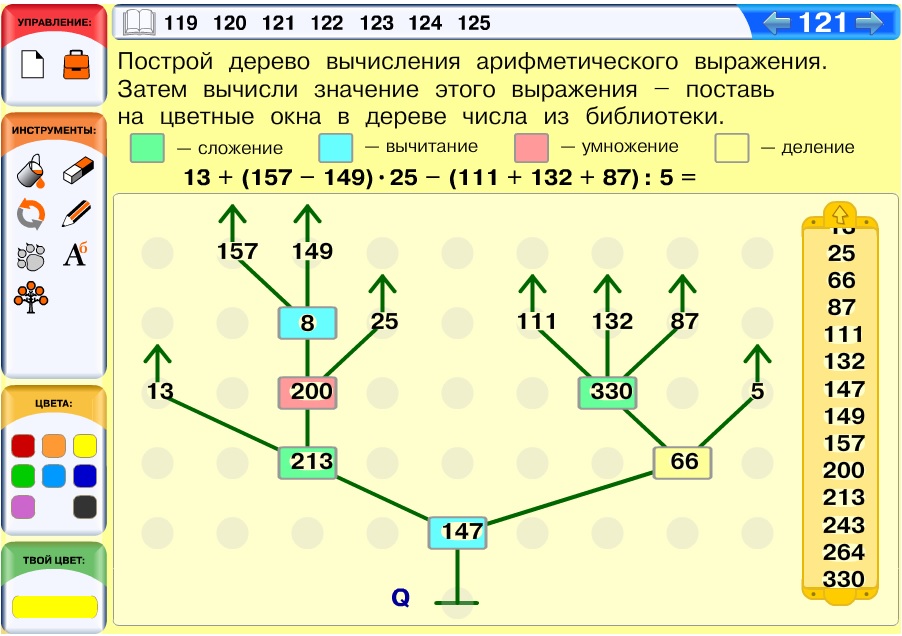
Задача 122. Задача о конструкции повторения в программе для Робика. Аналогичные задачи ребята уже решали.

Вариант решения:

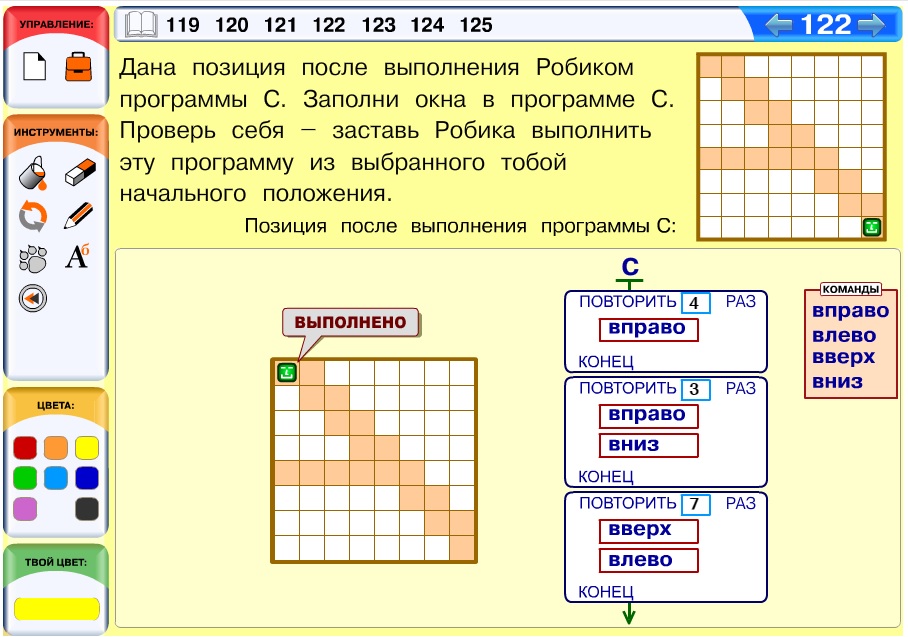
Задача 123. Повторение операции склеивания мешков цепочек. Всего в нашем распоряжении 8 цепочек. Существует лишь два варианта распределения цепочек: 2 • 2 = 4 и 0 • 8 = 0 (или 8 • 0 = 0). Второй вариант – «вырожденный» и скорее всего не придет в голову детям. Тем не менее он является верным: положить все 8 цепочек в один из мешков-аргументов. При умножении любого мешка на пустой мешок в результате получится пустой мешок. Таким образом, это верный вариант решения.

Рассмотрим первый вариант. Здесь 4 цепочки должны лежать в мешке-результате и по 2 цепочки надо разложить в мешки-аргументы. Ясно, что самые длинные цепочки (в нашем случае две цепочки длины 4) должны лежать в мешке-результате: 

Найдем цепочки, при склеивании которых получаются такие цепочки. Это цепочки     в первом мешке-аргументе и цепочка     во втором.

Разложим эти цепочки по мешкам:

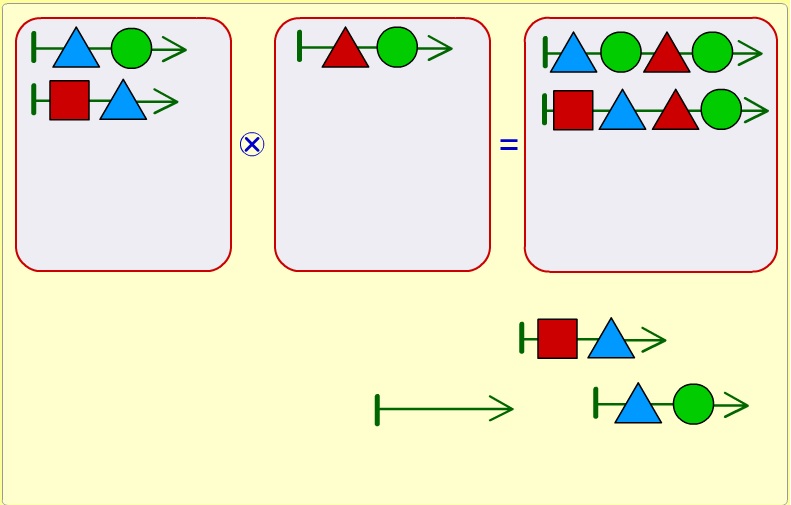
Осталась такая же пара цепочек, какую мы положили в первый мешок, и пустая цепочка. Кладём пустую цепочку во второй мешок, а две цепочки длины 2 – в мешок-результат. Сделав проверку, убеждаемся, что задача решена правильно:

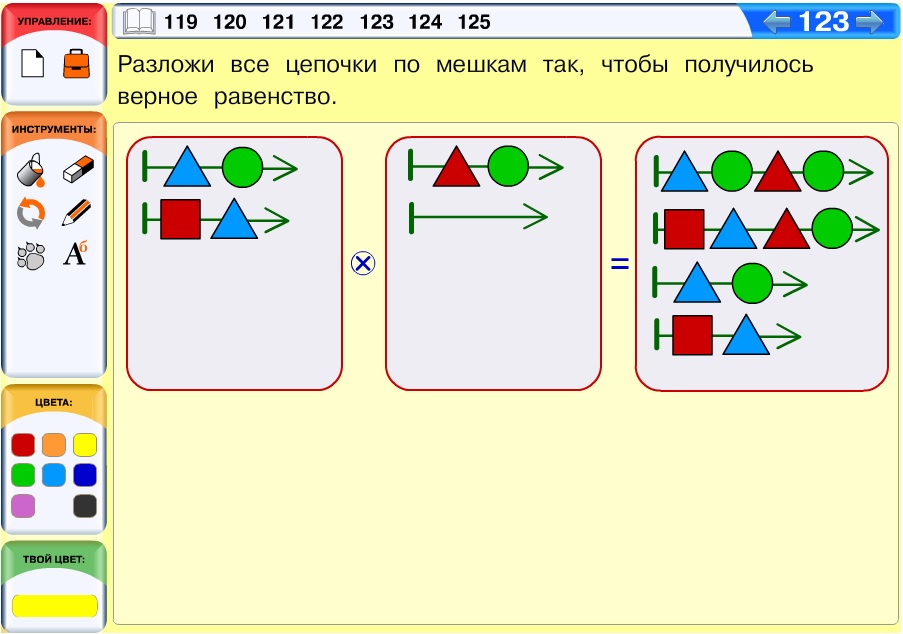
Задача 124. Сложность этой задачи состоит в том, что на позиции ровно 16 точек, а по условию партия должна закончиться на одиннадцатом ходу, то есть ползунок должен соединить всего 12 точек. Значит, через какие-то 4 точки отрезки проведены не будут. Если рассуждать подобным образом, то решение построить несложно.

Вариант решения:

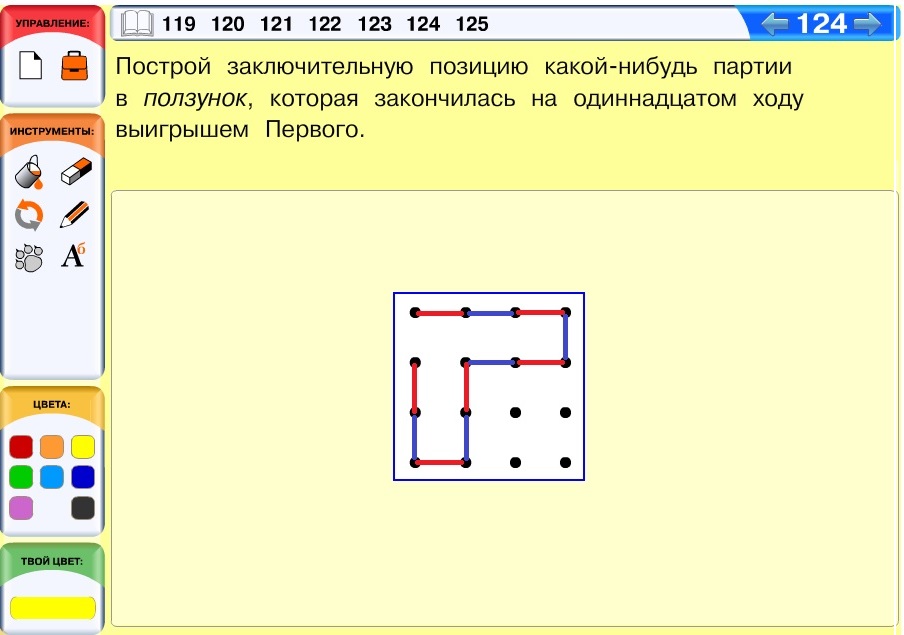
Задача 125. В случае возникновения затруднений стоит посоветовать учащемуся начать поиск пар одинаковых отрезков (сторон фигур) – отрезков, которые не просто одинаковой длины (это определить на глаз затруднительно), но которые расположены на сетке одинаково и при наложении совпадут. Фигуры с такими сторонами можно совместить без зазоров.

Ответ: