Информатика. 3–4 класс (часть 3) Демо+методичка

Уроки 9–10. «Выигрышные стратегии в игре камешки»

Работая с предыдущей темой, ребята анализировали в основном отдельные позиции игры камешки (и ходы, приводящие к ним). Теперь настало время проанализировать ход игры в целом. Перекидным мостиком между двумя этими темами является понятие разумной партии (и разумных ходов). Мы уже выяснили, что в разумной партии каждый игрок должен стараться следовать общему правилу – всегда оставлять противнику проигрышную позицию. В ходе решения задач ребята могли заметить, что в одной партии игры камешки только один из игроков может следовать этому правилу – тот, кто первым может занять выигрышную позицию. Теперь мы будем говорить, что такой игрок имеет выигрышную стратегию. Если он будет ей следовать, а, значит, делать только разумные ходы и оставлять противнику только проигрышные позиции, то выиграет при любой игре противника.

Итак, если игрок, имеющий выигрышную стратегию, будет ей следовать, то все возможные такие партии будут только разумными. Если начальная позиция выигрышная, то выигрышную стратегию имеет Первый, если проигрышная – Второй. Изложенное общее правило выигрыша – стараться оставлять противнику проигрышную позицию (оно верно для любой игры, где позиции можно разделить на выигрышные и проигрышные) в каждой игре камешки реализуется по-разному. Раскраска клеток числовой линейки определяет как игрока, обладающего выигрышной стратегией, так и его ходы (следование выигрышной стратегии). Правило выигрыша может быть сформулировано либо в виде последовательности ходов, которые должен делать игрок, либо в виде правила о том, какие позиции должен оставлять противнику данный игрок (если проигрышные позиции подчиняются некой общей закономерности). В следующих за данным листом определений задачах ребятам предстоит формулировать выигрышные стратегии в виде правила.

Решение задач из учебника

Задача 49. Первое, что ребята должны понять, изучая данный материал, что выигрышная стратегия действительно помогает выиграть одному из игроков и нужно научиться ей следовать. Именно поэтому мы начинаем серию задач на эту тему с маленького соревнования. Разрешенные ходы игры такие же, как на листе определений (1 и 2 камешка). Для следования выигрышной стратегии ребята используют раскрашенную числовую линейку с листа определений на с. 32, поэтому лучше посоветовать им не выбирать начальную позицию больше 10. Первое, что говорит о понимании ребятами материала листа определений: Первый выбирает в качестве начальной позиции выигрышную. В противном случае учащемуся надо посоветовать еще раз прочитать материал листа определений. Второе условие правильного выполнения задания – все сыгранные партии должны быть разумными, т. е. в цепочке партии все позиции, получающиеся после ходов Первого, – проигрышные. Чтобы вам легче было проверить соблюдение этих двух условий, попросите ребят записывать на черновике цепочки всех сыгранных партий. Если в каждой партии Первый действительно следует выигрышной стратегии, то оба утверждения в рамках должны быть истинными. С теми парами учащихся, у которых так не получилось, можно порассуждать вместе. На эту задачу не стоит жалеть времени, так как она является важным шагом при переходе от формального анализа отдельных позиций к содержательному анализу реальной игры.

Задача 50. В этой задаче проверяется понимание ребятами материала второй части листа определений – формулирования выигрышной стратегии в виде общего правила. Для начала стоит внимательно посмотреть на раскрашенную числовую линейку и выяснить, какой закономерности подчиняется размещение проигрышных позиций. Так видно, что на линейке существует четкое чередование позиций – проигрышная, две выигрышные, проигрышная, две выигрышные и т. д. Более того, все проигрышные позиции – числа, которые делятся на 3. Именно такие позиции должен оставлять противнику игрок, который первым сможет занять выигрышную позицию. В данном случае начальная позиция – число, которое делится на 3, она проигрышная, значит первым в выигрышной позиции окажется Второй и выигрышная стратегия имеется у него.

Задача 51. Здесь проверяется, может ли учащийся применить полученную в предыдущей задаче выигрышную стратегию для построения разумной партии игры. На предыдущем уроке ребята уже строили такие партии, но только с опорой на раскрашенную линейку. Здесь ребенок может использовать начало такой линейки и правило выигрышной стратегии. Так, в данной задаче начальная позиция на 3 не делится, значит она выигрышная и выигрышную стратегию имеет Первый. Первая ближайшая проигрышная позиция – 24 камешка, значит первый ход Первый должен сделать именно в нее. Дальше Первый продолжает делать ходы только в проигрышные позиции: 21, 18, 15 и т. д.

Задача 52. На листе определений данная игра камешки (с ходами 1, 2 и 3 и любой начальной позицией) обсуждена полностью и исчерпывающе – сформулировано правило выигрышной стратегии, которое позволяет для любой начальной позиции определить обладателя выигрышной стратегии и научить его обыгрывать своего соперника. В частности, это правило позволяет легко раскрасить числовую линейку, ответить на вопросы и построить разумные партии. Тем не менее, кто-то из ребят будет решать задачу так же, как на предыдущем уроке. Таких не надо останавливать, для них это дополнительная возможность повторить материал. Если вам важно, чтобы дети в этой задаче использовали сформулированную на листе определений выигрышную стратегию, предложите им по окончании решения большие начальные позиции, для которых раскрасить числовую линейку затруднительно.

Задача 53. Данная задача напоминает задачу 49. Разница в том, что здесь детям предлагается играть партии без опоры на числовую линейку, с использованием только правила выигрышной стратегии (сформулированного на листе определений), именно поэтому начальные позиции должны быть больше 20. Кому-то это может показаться сложным. Критерии правильности работы учащихся описаны в комментарии к задаче 49. Если вы видите, что Первый все же проигрывает, порассуждайте вместе с детьми, опираясь на материл уже решенных задач 49 – 52. Особенно стоит обратить внимание на построение разумной партии игры в задаче 51.

Задача 54. Здесь ребята вспоминают тему «Конструкция повторения» и ситуацию вложенного цикла.

Ответ:

Задача 55. Эта задача полностью аналогична тем, которые ребята решали на предыдущем уроке. Предоставьте учащимся достаточно времени, чтобы справиться с ней самостоятельно. Данную задачу удобно использовать для текущего контроля (предыдущей темы).

Задача 56. Задача на повторение лексики, относящейся к цепочкам, в частности, понятий «раньше/позже» и «перед каждой/после каждой». Первым можно использовать второе утверждение и найти место для буквы К. Эта буква будет первой в слове. Теперь попробуем найти место для трех букв О. У нас имеется 5 пустых окон. В одном из них (после буквы Ы) буква О стоять не может. Также две буквы О не могут идти подряд (иначе не будет истинным первое утверждение). Значит одна буква О стоит в последнем окне, а две другие – во втором и четвертом окне. Теперь используем последнее утверждение и получим слово КОРОМЫСЛО.

Задача 57. Эта задача уже на текущий (новый!) лист определений. Раскрасив (в задаче 55) числовую линейку, ребята замечают, что все позиции, делящиеся на 3, – проигрышные, а все остальные – выигрышные. Поэтому при начальной позиции 212 камешков выигрышную стратегию имеет Первый. Он должен всегда забирать столько камешков, чтобы Второму оставалось число камешков, кратное трем. Так на своем первом ходу Первый должен забрать 2 камешка и оставить Второму позицию 210 камешков.

Задача 58. Необязательная. Задача аналогичная задаче 53. Проведение соревнования, как обычно, потребует некоторого дополнительного времени. Поэтому при дефиците времени данную задачу можно пропустить.

Задача 59. Необязательная.  Здесь ребята повторяют лист определений «Перед каждой, после каждой», а также «Если бусины нет». Можно сразу отбросить (например, вычеркнуть) те цепочки, где круглая бусина – последняя (у нее «первой бусины после» вообще нет), таких цепочек оказывается 4. Из оставшихся 7 подходят лишь 5 цепочек, причем в четырех из них круглая бусина одна (возможно, кто-то из ребят забыл о том, что конструкцию «после каждой» можно употреблять и в этом случае).

Ответ:

Задача 60. Необязательная. Задача на повторение темы «Все пути дерева». Проверьте, что все помнят алгоритм построения всех путей дерева, который детально рассматривался во второй части курса. Лучше всего, если ученик использует при этом некоторую систему пометок. Мы советовали помечать каждый лист после того, как выписан ведущий в него путь. Хорошо также, если ученик имеет систему перебора листов (например, сверху вниз). Особое внимание необходимо обратить на детей, которые выписывают пути как попало и при этом делают ошибки. 

Ответ:

МЕЛ    МОЗГ СОМ
МЕЛЬ МОЛ   СОЛО
МЕХ   МОСТ СОЛЬ
МЕЧ   МОХ

Задача 61. Три команды, уже заданные в программе, дают ребятам ключ к решению, поскольку на поле имеется лишь одна клетка, из которой Робик, не выходя за пределы закрашенной фигуры, может выполнить серию команд вниз–вверх– вверх: это центральная клетка второй строки. Следующий вопрос, который нужно решить детям: из какой клетки Робик начинал свой путь, если он добрался до упомянутой выше клетки за 4 команды? При этом нужно учитывать фигуру, которую закрасил Робик в процессе выполнения программы – нельзя выходить за ее пределы. Клетку положения Робика на поле в начальной позиции можно искать перебором. Таких возможных клеток оказывается две – вторая и шестая клетки второй строки. Отсюда возможных программ Т тоже две.

Ответ:

Задача 62. Необязательная. Сложность данной задачи в том, что фигурки похожи между собой. Все они звезды, которые отличаются только числом лучей. Чтобы не сбиться, полезно считать число лучей. Можно использовать деление звезд на группы с одинаковым числом лучей по ходу решения. Например, в левом мешке всего две пятиконечные звезды – синяя и зеленая. Найдем пятиконечные звезды в правом мешке. Их две и обе нераскрашенные, значит раскрасим одну из них в синий цвет, а другую – в зеленый. Лучше сразу после этого соединить одинаковые пятиконечные звезды в пары. После этого можно перейти к шестиконечным звездам и т. д. 

Компьютерный урок «Выигрышные стратегии в игре камешки», 1 часть, задачи 50 – 56

Задача 50. Аналогично задаче 50 из учебника, в этой задаче проверяется понимание ребятами материала второй части листа определений – формулирования выигрышной стратегии в виде общего правила. Для начала нужно раскрасить числовую линейку: 

Видно, что на линейке существует чередование позиций – проигрышная, две выигрышные, проигрышная, две выигрышные и т. д. Все проигрышные позиции – числа, которые делятся на 3. Число 198 делится на 3. Значит, Первый будет начинать игру с проигрышной позиции, а Второй первым окажется в выигрышной позиции и выигрышная стратегия имеется именно у него. 

Ответ.
Выигрышная стратегия есть у Второго.
Он должен на каждом ходу забирать столько камешков, чтобы противнику оставалось ЧИСЛО (КАМЕШКОВ), КОТОРОЕ ДЕЛИТСЯ НА 3 (или КРАТНОЕ 3).

Задача 51. Сначала раскрашиваем числовую линейку:

Теперь видно, что проигрышные позиции в этой игре ‒ это числа, которые делятся на 4. Начальная позиция ‒ 32 камешка. Число 32 делится на 4. Значит, Первый будет начинать игру с проигрышной позиции, а выигрышная стратегия имеется у Второго.

Вот одно из возможных решений задачи:

Задача 52. В предыдущей задаче 51 ребята закрашивали числовую линейку до 15 для игры с такими правилами и выяснили, что проигрышные позиции в этой игре – числа, которые делятся на 4. Поэтому раскрасить числовую линейку до 23 будет совсем несложно:

Чтобы ответить на вопросы задачи, нужно проанализировать позиции 23 и 24. Позиция 23 – выигрышная, значит, выигрышную стратегию будет иметь Первый. Число 24 кратно четырём, значит, позиция 24 будет проигрышной, и выигрышную стратегию будет иметь Второй.

Кто из игроков имеет выигрышную стратегию в игре с такими правилами и начальной позицией 23 камешка?
Ответ: ПЕРВЫЙ.

Кто из игроков имеет выигрышную стратегию в игре с такими правилами и начальной позицией 24 камешка?
Ответ: ВТОРОЙ.

Задача 53. 

Как мы выяснили, решая задачи 51 и 52, проигрышными позициями в игре с такими правилами будут числа, которые делятся на 4. Число 234 не делится на 4, значит, позиция 234 – выигрышная.

Ответ.  Выигрышную стратегию имеет Первый. Стратегия заключается в том, что он должен на каждом ходу забирать столько камешков, чтобы противнику оставалось ЧИСЛО КАМЕШКОВ, ДЕЛЯЩЕЕСЯ НА 4.

Задача 54. Эта задача похожа на компьютерные задачи 10 и 32. Заключительная позиция уже задана, количество позиций в библиотеке ограничено, поэтому партию удобнее строить с конца. Сначала найдем в библиотеке позицию, предыдущую перед заключительной. Оказывается из четырех данных позиций нам подходит лишь одна. Так мы двигаемся от конца к началу цепочки, на каждом шаге позиция определяется однозначно.

Задача 55. Подходящих деревьев здесь довольно много. Уровней в дереве может быть от двух до четырех, поскольку подходящее дерево из одного уровня построить не удается (подумайте, почему!), а длина каждого пути меньше пяти. После того как мы определились с числом уровней, на каждый уровень можно сразу поместить по 7 бусин. При этом на последнем уровне будет 7 листьев. Значит, еще один лист (и только один!) дерева должен быть не на последнем уровне.

Задача 56. Начинать строить цепочку можно с любого слова. Возьмем, например, НОРИЛЬСК. После этого слова в цепочке могут стоять КОРОЛЁВ или КОВРОВ. Оба слова заканчиваются на одну букву, поэтому дальше выбираем между словами ВОРКУТА, ВИЛЬНЮС или ВЛАДИМИР. И так далее. В результате может получиться, что не все данные топонимы вошли в построенную цепочку. В этом случае цепочку можно подредактировать, благо при решении задачи на компьютере сделать это несложно. Например, поставить в начало цепочки (перед НОРИЛЬСКОМ) слово МАГАДАН. В результате проб и ошибок выяснится, что слово МАГАДАН может стоять только в начале цепочки (потому что в наборе нет слов, которые заканчиваются на М), а слово ВИЛЬНЮС – только в конце цепочки (потому что в наборе нет слов, которые начинаются с С).

Вот пример цепочки, в которой участвуют все данные топонимы:

Компьютерный урок «Выигрышные стратегии в игре камешки», 2 часть, задачи 57 – 63

Задача 57. Рассуждая так же, как при решении компьютерной задачи 44 или задачи 40 из учебника, раскрашиваем числовую линейку:

Теперь ответить на вопросы задачи будет несложно.

Кто из игроков имеет выигрышную стратегию в игре с такими правилами и начальной позицией 22 камешка?
Ответ: ПЕРВЫЙ.

Кто из игроков имеет выигрышную стратегию в игре с такими правилами и начальной позицией 21 камешек?
Ответ: ВТОРОЙ.

Задача 58. Анализируя числовую линейку, мы видим, что проигрышными являются все позиции, числа в которых кратны числу 7, а также позиции, которые на 2 больше каждой позиции, кратной семи: (7a+2). Поэтому для ответа на вопросы задачи нужно разделить 210 на 7.
210 : 7 = 30
Число 210 кратно 7, значит, позиция 210 ‒ проигрышная. 

Ответ.  Выигрышную  стратегию  имеет  ВТОРОЙ.  Стратегия  заключается  в  том,  что  он  должен  на  каждом  ходу  забирать  столько  камешков,  чтобы  противнику  оставалось ЧИСЛО КАМЕШКОВ, ДЕЛЯЩЕЕСЯ НА 7 или ДЕЛЯЩЕЕСЯ НА 7 ПЛЮС ЕЩЁ 2.

Задача 59. Используя рассуждения, проведенные при решении предыдущей задачи 58, сначала разделим число 211 на 7:
211 : 7 = 30 (остаток 1)
Число 211 не кратно семи, на числовой полоске число 211 ‒ следующее после числа 210. Значит, позиция 211 камешков – выигрышная.

Ответ.  Выигрышную  стратегию  имеет  ПЕРВЫЙ.  Стратегия  заключается  в  том,  что  он  на  первом  ходу  должен  взять  1  камешек,  а  затем  на  каждом  ходу  забирать  столько  камешков,  чтобы  противнику  оставалось  ЧИСЛО КАМЕШКОВ, ДЕЛЯЩЕЕСЯ НА 7 или ДЕЛЯЩЕЕСЯ НА 7 ПЛЮС ЕЩЁ 2.

Задача 60. Знакомая ребятам задача на построение партии игры в ползунок. Думаем, к настоящему моменту все ребята уже усвоили закономерности определения выигравшего игрока. Чтобы выиграл Второй, нужно чтобы ломаная состояла из четного числа звеньев. Соответственно нужно, чтобы она проходила через нечетное число точек поля. Например, можно построить ломаную, проходящую через 11 или 9 точек поля.  Конечно, эти рассуждения вам пригодятся для контроля правильности решения – дети наверняка будут строить ломаную, моделируя реальную игру, а не строя подобные рассуждения.

Вот одно из возможных решений:

Задача 61. В курсе 3 класса таких задач было довольно много. Как видим, при построении дерева мы должны «экономить» бусины и стараться не размещать несколько одинаковых бусин на одном уровне в том случае, если можно обойтись одной. В данном случае первые бусины всех путей одинаковые, но в одном пути эта же оранжевая треугольная бусина является последней – она должна быть листом в дереве. Поскольку бусина в дереве не может быть одновременно и листом, и не листом, то на первый уровень ставим две оранжевые треугольные бусины, одну из них помечаем стрелкой (она является листом).

На втором и третьем уровне ситуация будет аналогичной – мы опять размещаем по две одинаковые (синие круглые и красные квадратные) бусины (лист и не лист). На четвертом уровне будет одна (желтая) бусина. Осталось проверить, что в нашем дереве ровно 7 бусин.

Задача 62. Сложность этой задачи  заключается в том, что количество повторов в конструкции повторения не задано. Поэтому начинаем решение с анализа пути Робика – попробуем разбить рисунок, раскрашенный Робиком, на одинаковые части. Например, так:

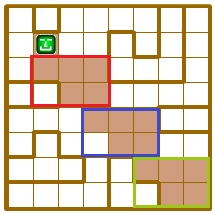
У нас получилось три повтора. Теперь нужно определить, из каких команд состоит конструкция повторения – как заставить Робика нарисовать один выделенный кусок и оказаться в его правом нижнем углу. Задача имеет несколько решений, но первые две команды цикла определяются однозначно ‒ вниз и вправо (Робик просто не может выполнить другие команды в начале пути).

Задача 63. Сложность этой задачи состоит в том, что не все заданные слова должны участвовать в нашей цепочке: во-первых, не все слова являются топонимами, а во-вторых, не все топонимы можно будет использовать в построенной цепочке – длина цепочки меньше числа топонимов.

Сначала надо отделить слова-топонимы от остальных (что само по себе может оказаться сложным для ребенка делом), а потом уже из слов-топонимов нужно выбрать подходящие для построения цепочки. Один из вариантов – строить цепочку из частичных решений, а затем попытаться составить их между собой.

Вот один из возможных вариантов решения задачи: