Информатика. 3–4 класс (часть 3) Демо+методичка

Урок 7. «Игра сим»

Эта игра, хотя и использует в качестве поля игры окружность, лишь в малой степени является геометрической (в отличие, например, от игры ползунок). Сим – игра, скорее, просто комбинаторная. Математики и другие профессионалы, использующие математический аппарат, имеют определенное представление о том, когда та или иная задача или метод ее решения являются геометрическими, алгебраическими, аналитическими, комбинаторными, вероятностными и т. д. В последнее время в математике часто говорят о «нелинейных» задачах. Вероятно, вырисовывается и некоторый класс алгоритмических, информатических задач. Хотя эти различия и не входят в школьный курс, но они могут оказаться вам полезными при анализе того стиля, в котором дети пытаются решать задачи, того, почему задачи одного типа получаются у одних детей, а другого – у других.

В отличие, например, от игры крестики-нолики, игра сим может для большинства ребят оказаться незнакомой. Кроме того, по сравнению со всеми предыдущими играми здесь сложнее определить заключительную позицию, особенно если одноцветный треугольник не возник. Действительно, в игре камешки заключительная позиция видна всегда, в игре крестики-нолики отсутствие ряда из трех одинаковых значков и наличие свободных клеток говорит о возможности продолжения игры. О том же в игре ползунок говорит наличие свободных точек, с которыми может быть соединен хотя бы один из концов ползунка. В игре сим, если точек на окружности много (больше четырех), дети могут легко не заметить того, что какие-то точки еще не соединены, и закончить игру преждевременно. Обратите на это внимание ваших учеников. Обсудите с ними, сколько всего отрезков может выходить из одной точки (на один меньше, чем всего точек). Таким образом, простой проверкой того, остались ли еще возможные ходы, является пересчет отрезков, выходящих из каждой точки.

Решение задач из учебника

Задача 34. Первая после листа определений задача, как обычно, предлагается детям для того, чтобы они освоились с новыми понятиями, в данном случае – с правилами игры сим. На начальном этапе ребятам наверняка потребуется некоторый контроль. Например, после того как учащиеся поработали с листом определений, есть смысл провести несколько партий игры сим на доске под контролем всего класса. При проведении кругового турнира в группах можно для каждой партии назначить одного-двух контролеров. Несмотря на то что при проведении двух партий одновременно турнир можно закончить гораздо быстрее, все-таки лучше, чтобы процесс игры многократно проверялся (не только игроками, но и контролерами). Чтобы контролерам в группах было проще проверять, является ли данная позиция заключительной, можно перед началом партий вместе обсудить, сколько всего должно быть проведено отрезков в случае ничьей (на окружности с пятью точками) и с какого хода могут появляться одноцветные треугольники. Конечно, на листе определений ребята уже читали, что в случае ничьей на окружности с пятью точками игроки делают по 5 ходов (проводят всего 10 отрезков), однако учащимся полезно убедиться в этом самим.

Надеемся, что с заполнением турнирной таблицы у ребят трудностей не возникнет: ведь подобные задания они уже выполняли для других игр.

Задача 35. В отличие от предыдущей задачи каждый учащийся здесь играет за Первого, за Второго и сам же является контролером. С одной стороны, это проще, ведь можно «подыгрывать». Например, если ребенок хочет закончить партию побыстрее, он может завершить цепочку партии уже на шестой позиции. С другой стороны, каждый ученик теперь должен сам следить за соблюдением правил игры, в частности, за соблюдением очередности хода, за тем, чтобы на каждом ходу появлялся только один отрезок, за тем, чтобы все ходы аккуратно переносились с предыдущей позиции на следующую.

Провести проверку поможет указание. Действительно, если некоторая позиция заключительная, то либо есть одноцветный треугольник, либо все точки на окружности соединены. Первое проверить достаточно просто. Если в предыдущей задаче вы обсуждали с ребятами, сколько отрезков на окружности с пятью точками должно выходить из каждой точки в случае ничьей, то достаточно просто посчитать это в заключительной позиции, если нет – можно обсудить вопрос о числе отрезков в этой задаче.

Мы приводим один пример цепочки игры с заданным началом, в которой каждый из игроков стремился к выигрышу:

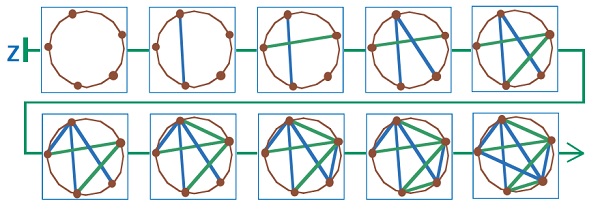
Задача 36. Эта задача сложнее, чем задача 35. Здесь нужно сначала спланировать решение на черновике (например, на пустом поле с листа вырезания) и только потом построить цепочку позиций, воспользовавшись заготовками с листа вырезания. Нужно вспомнить правила игры, понять, какая позиция будет выигрышной для Второго – это треугольник из синих отрезков (ведь Второй выигрывает, когда проигрывает Первый). Некоторые дети могут строить решение этой задачи довольно долго. Другие могут найти простое решение сразу. И тот и другой случай представляет определенный интерес.

Короткое решение основывается на том, что Первый может стремиться к проигрышу, а Второй просто не должен ему мешать. При таком подходе ясно, что очередной ход Второго может быть почти любым, а следующий ход Первого замыкает треугольник и немедленно приводит его к проигрышу:

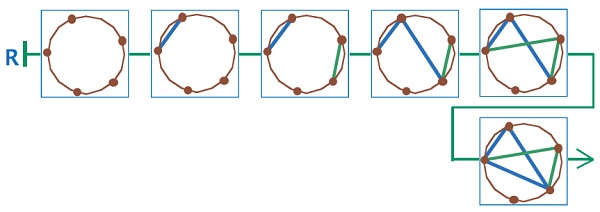
Это простое построение не смогут провести дети, которые захотят, чтобы Первый играл «правильно», «разумно», «не поддавался» и т. д. Таким образом, здесь есть, что обсудить и в чем разобраться. Если будет время, предложите детям самим поиграть в сим с данным началом игры (можно опять-таки использовать пустые поля с листа вырезания, которые мы специально заготовили с запасом). Затем можно собрать заключительные позиции разных партий, в которых выиграл Второй, и обсудить их.

Вот одна из цепочек игры с «разумной» игрой обоих игроков:

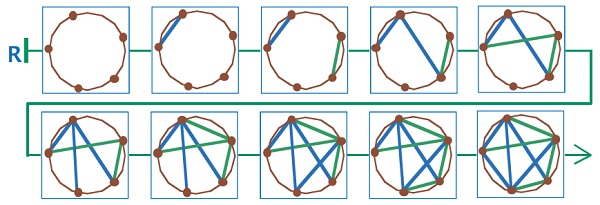
Задача 37. По содержанию эта задача наиболее близка к задаче 28, но в отличие от нее является обязательной. Вполне возможно, что некоторым учащимся понадобится ваша помощь. Большинство ребят, скорее всего, будут решать задачу методом проб и ошибок – строить ломаную ползунка как-нибудь. Лучше всего сначала делать это на запасных полях с листа вырезания.

Соображения, приведенные в задаче 28 о соотношении числа звеньев ломаной (т. е. числа ходов) и точек на поле, через которые прошел ползунок, позволяют сделать вывод, что в заключительной позиции цепочки W ползунок должен пройти через все 12 точек поля, а в заключительной позиции F – через 11 точек поля. Хорошо, если сильные ребята постепенно будут усваивать подобные закономерности. При этом всем ребятам необходимо понимание того, что число сделанных ходов определяет число звеньев ломаной ползунка. Таким образом, вам, проходя по классу, достаточно будет обратить внимание учащегося на то, что построенная им ломаная не соответствует требуемому числу ходов. Подходящих цепочек много. Мы приводим одну цепочку W и одну цепочку F.

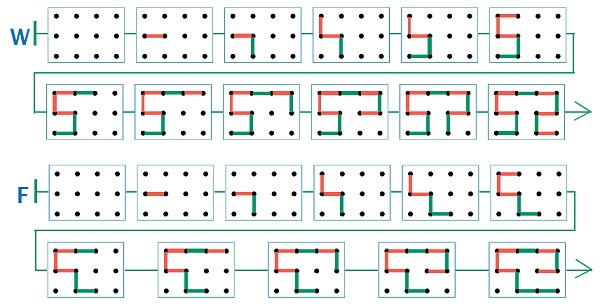
Задача 38. Необязательная. Если вы хотите предложить эту задачу средним или слабым учащимся, лучше заранее сделать несколько копий фигурок из этой задачи. Тогда можно посоветовать ребятам вырезать фигурки и составить цепочку на столе, передвигая фигурки. Строим сначала несколько фрагментов цепочки, например «крокодил – слон», «тигр – слон – жираф» (этот фрагмент строим с конца). Потом построенные фрагменты объединяем в одну цепочку.

Задача 39. Необязательная. Подобная задача ребятам уже встречалась (см. комментарий к задаче 29). Поэтому данную задачу можно использовать для повторения и обобщения на более высоком уровне. Например, если, решая задачу 29, ребята писали цепочки парий формально, попросите их здесь составлять цепочки «честной» игры, где ни один игрок не поддается и каждый пытается выиграть (впоследствии мы назовем такую парию разумной). Для этого лучше всего подойдет игровой вариант решения – сыграть с соседом несколько партий в камешки по данным в задаче правилам и обобщить закономерные игровые ситуации. Так, в ходе игр становится ясно, что если Первый на первом ходу взял 3 камешка, то Второй при «честной» игре на втором ходу возьмет 3 оставшихся камешка и выиграет. Если же Первый на первом ходу возьмет 4 камешка, то Второй проиграет в любом случае. Если же Первый на первом ходу берет 1 камешек, то игра может сложиться по-разному, в зависимости от следующего хода Второго. Можно проводить обобщение в другом направлении. Например, спросить у ребят, можно ли по длине цепочки партии сразу определить победителя. Да, если цепочка четной длины, то выигрывает Первый, если нечетной – Второй. Значит, задача сводится к тому, чтобы написать две цепочки игры – четной и нечетной длины.

Компьютерный урок «Игра сим», задачи 36 – 42

Задача 36. Задача на усвоение правил новой игры сим. Задача эта аналогична задачам на цепочку игр крестики-нолики или ползунок. Здесь правильный порядок позиций тоже можно установить формально, ориентируясь только на число отрезков в позиции, поскольку на каждом ходу игры на поле добавляется ровно 1 отрезок.

Задача 37. Эта задача сложнее похожей на нее задачи 35 из учебника, поскольку здесь задана длина цепочки. Всего на окружности с пятью точками можно построить 10 отрезков. Длина нашей цепочки 9, значит в игре было сделано 8 ходов. Таким образом, делаем вывод, что игра закончилась не вничью (когда все возможные отрезки нарисованы, а выигрыша не получилось), а закончилась раньше выигрышем одного из игроков. При этом последний ход сделал Второй (поскольку в игре было сделано 8 ходов) и он проиграл. Следовательно, на поле в заключительной позиции должно быть 8 отрезков и ровно один треугольник из синих отрезков. Треугольников из красных отрезков на поле быть не должно. Один из вариантов решения этой задачи – сначала построить заключительную позицию, удовлетворяющую всем описанным условиям, а потом построить какую-нибудь партию, приводящую к этой заключительной позиции. Можно делать и наоборот – строить игру от начала к концу, следя за выполнением всех условий и правил игры.

Задача 38. Ещё одна задача на усвоение правил игры сим. Наиболее простой способ решения этой задачи – сыграть с товарищем партию в сим на бумаге, а затем перенести заключительную позицию на экран. Или играть «самому с собой» и поочередно рисовать отрезки красным и синим. По окончании игры попросите ребят обязательно провести проверку выполнения всех правил игры.

Задача 39. Очередная задача на построение цепочки игры в камешки. На вопрос задачи можно ответить ещё до построения цепочки, так как четвёртый ход в игре делает Второй и тем самым выигрывает.

Задача 40. Продолжаем работу с игрой ползунок. Эта задача аналогична компьютерной задаче 30. Мы пока не обсуждали понятия «разные позиции». Если в беседе с кем-то из ребят такой вопрос возникнет, то можно определить разные позиции пока так же, как мы определяли разные фигурки. Подробнее мы обсудим это с ребятами в проекте «Стратегия победы».

Задача 41. Задача о порядке дней недели. В курсе 3 класса было много аналогичных задач, поэтому, скорее всего, все ребята справятся с ней самостоятельно.

Задача 42. Задача комбинаторного характера. Однако дети, как правило, решают такие задачи методом проб и ошибок, без всякого перебора. Даже если дети в таких задачах и проводят какие-то рассуждения, то больше из соображений здравого смысла, чем классической математики. Тем не менее, задача имеет вполне формальное решение. Улиток всего 9, в каждой по 2 области. Значит можно раскрасить одну из областей (например, раковину) у трёх улиток в красный цвет, у трёх – в синий, у трёх – в зелёный. Теперь у каждых трёх улиток, у которых раковина раскрашена одинаково, нужно тело раскрасить по-разному. Тогда все фигурки будут разными.