Информатика. 3–4 класс (часть 3) Демо+методичка

Урок 6. «Игра ползунок»

Эта игра интересна тем, что в ней место числовой интуиции занимает геометрическая. При этом геометрия здесь не обычная, которую учат в школе, а более современная – это, можно сказать, дискретная топология (дискретная потому, что в ней действие разворачивается в пространстве конечного числа точек, а топология потому, что для нас несущественно расстояние между этими точками, а существенно только их взаимное расположение – какая с какой является соседней).

Решение задач из учебника

Задача 25. При решении данной задачи ребятам предстоит освоить правила новой игры – игры ползунок. Поэтому, проходя по классу, постарайтесь проконтролировать соблюдение всеми игроками правил игры, при необходимости возвращайте ребят к листу определений. Возможно, стоит в первых партиях турнира в каждой группе назначить контролера (или двух), которые будут следить за соблюдением правил игры. Другой вариант – сыграть на доске несколько тренировочных партий.

Если вам приходилось играть в ползунок на поле 3×3, то вы, скорее всего, заметили, что Второй выигрывает здесь гораздо чаще, чем Первый. На самом деле Второй в этой игре имеет выигрышную стратегию, т. е., следуя определенным правилам, он может выиграть всегда, как бы ни играл Первый (мы еще будем много говорить о выигрышных стратегиях в дальнейшем, в частности, и в игре ползунок на поле 3×3). Если вы хотите, чтобы члены группы были в равном положении, то предложите ребятам перед началом каждой партии кидать жребий, кто будет Первым (с помощью кубиков, спичек, игры «Камень, ножницы, бумага» и пр.). Поскольку в игре ползунок ничьих не бывает, заполнять турнирную таблицу будет немного легче, чем для игры крестики-нолики, и победителя будет легко определить, даже если у двух игроков наберется одинаковое число очков. Если же число очков будет одинаковым сразу у троих игроков (в группе из трех человек или у троих из четырех), то для определения победителя придется проводить дополнительные партии.

Задача 26. Здесь от учащихся требуется лишь понимание правил игры ползунок. Напомните ребятам, что нужно каждый новый отрезок проводить красным или зеленым карандашом в зависимости от того, кто делает ход. Как и в аналогичных задачах с игрой крестики-нолики, необходимые поля ребята найдут на вкладыше.

Очень важно, чтобы решение задачи закончилось проверкой. Указание в конце задачи призвано облегчить ребятам процедуру проверки на первых порах. Главное условие – чтобы последняя позиция в цепочке действительно была заключительной. Для этого на поле должна получиться ломаная, которую уже нельзя продолжить. Также нужно проверить, чтобы при переходе от каждой позиции к следующей добавлялся ровно один отрезок. Наконец, стоит просмотреть всю цепочку, проверяя, соответствует ли очередность хода цвету появившегося отрезка (можно над каждой позицией пометить римскими I или II того, кто сделал данный ход) и соответствует ли следующая позиция предыдущей (все отрезки предыдущей позиции должны повториться и на следующей).

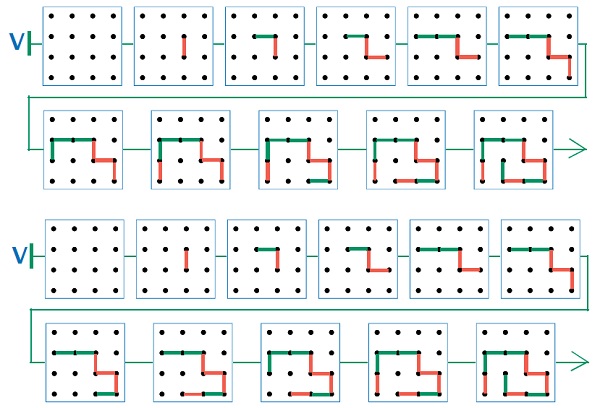
Задача 27. Здесь предстоит построить цепочку позиций игры ползунок с заданной заключительной позицией. Как и при решении задачи 7, учащийся может двигаться от начала к концу, следя за тем, чтобы на поле на каждом ходе появлялся только такой отрезок, который есть в заключительной позиции (учитывая и цвет), или от конца к началу, убирая по одному отрезку от одного из концов ломаной. В обоих случаях учащийся должен следить за соблюдением очередности хода, чтобы при каждом переходе от одной позиции к другой появлялся (или исчезал) отрезок соответствующего цвета. Несмотря на внешнюю однотипность задач 27 и 7, данная задача оказывается существенно сложнее. Это связано со спецификой игры ползунок. В отличие от игры крестики-нолики, где значки, которые игроки ставят на поле, не должны быть никак связаны между собой, в игре ползунок каждый следующий отрезок должен присоединяться к уже нарисованной ломаной. Учитывая, что отрезок должен быть еще и определенного цвета, мы приходим к тому, что в данной задаче в качестве первого хода Первого нельзя брать любой из красных отрезков в заключительной позиции. В противном случае мы сталкиваемся с тем, что цепочку игры в некоторый момент нельзя продолжить и привести к заключительной позиции. Перебирая все возможные первые ходы Первого (красные отрезки в заключительной позиции) и пытаясь строить с каждым из них цепочку партии игры, мы приходим к выводу, что цепочку V позволяет построить лишь один из них (вертикальный верхний). Далее вплоть до шестой позиции вариантов при выборе следующего хода ни у Второго, ни у Первого нет. Таким образом, в данной задаче (в отличие от задачи 7) существуют лишь две подходящие цепочки V (см. ответ).

Описанные выше особенности игры ползунок объясняют то, что данную задачу проще решать с конца, отбрасывая постепенно отрезки соответствующих цветов, ведь вариантов при выборе отрезка, который можно отбросить, существенно меньше.

Здесь мы уже не напоминаем учащемуся в условии о необходимости проверки, но это не значит, что она не нужна. Например, можно провести парную проверку, попросив ребят поменяться тетрадями. Полезно при этом предварительно спросить ребят, какие ошибки при решении могут быть допущены.

Ответ: вот два возможных варианта цепочки V:

Задача 28. Необязательная. В этой задаче наиболее естественный путь решения – экспериментальный. Надо предложить детям порисовать на черновике (например, на таком же поле с листа вырезания) несколько вариантов партий с заданным началом. Учащиеся, по сути дела, будут пользоваться методом случайного перебора вариантов. В этих попытках партии иногда будут заканчиваться, еще до одиннадцатого хода, иногда одиннадцатый ход может быть не последним – ведь останутся возможные ходы. В ходе таких экспериментов у детей возникнет ощущение того, «как все устроено», и требуемый ход игры будет найден. Учителю здесь, как обычно, отводится роль консультанта, проверяющего точность следования правилам игры ползунок.

Для того чтобы быстро проверить решение или подтолкнуть затрудняющегося в решении ученика, помогут некоторые математические (точнее, геометрические) соображения. Понятно, что, если отвлечься от раскрашивания отрезков в красный и зеленый цвета, то задача сводится к тому, чтобы дополнить имеющиеся 3 звена до ломаной из 11 звеньев, которую нельзя продолжить. Ломаная линия из 11 звеньев проходит через 12 точек. Это значит, что на нашем поле она не пройдет через какие-то 4 из 16 точек поля. Таким образом, задача сводится к тому, чтобы построить ломаную, включающую заданный отрезок из 3 звеньев, не проходящую через какие-нибудь 4 точки поля, и такую, что ее нельзя продолжить. Можно сделать это по-разному, например, так:

Такие рассуждения дают нам не только решение задачи, но и подход к более широкому кругу вопросов, возникающих вокруг данной задачи. Например, возможна ли такая партия игры ползунок на этом поле 4×4, в которой выигрывает Второй? Да, если мы сможем построить ломаную из четного числа звеньев. Сколько ходов вообще может быть в игре на поле 4×4, например, может ли быть 20 ходов? Нет, так как точек на поле всего 16, а значит, ломаная может состоять не более чем из 15 звеньев (ходов).

Вы можете обсуждать вышеперечисленные вопросы, а можете совсем их не касаться. Однако приведенные рассуждения могут вам помочь в тот момент, когда у ребенка работа над задачей застопорилась. Если вам хотелось бы не подсказывать ему решение, а лишь навести на мысль о том, «как все устроено», то достаточно будет замечаний типа: «Ты захватил в ползунок слишком много точек поля, поэтому ходов больше, чем требуется. Попробуй оставить в стороне какие-то точки», или что-то в этом роде в зависимости от ситуации.

Решений в данной задаче достаточно много. Поучительно сравнить решения, полученные разными ребятами, и выделить в них общее.

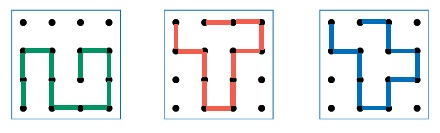
Ответ: приводим одну из цепочек возможных партий:

Задача 29. Возможных партий игры камешки по таким правилам не так уж и много, всего 6. В двух из них выигрывает Второй:

5–4–0 и 5–1–0

В остальных выигрывает Первый:

5–4–1–0; 5–4–3–0; 5–4–3–2–1–0; 5–2–1–0.

Для начала можно написать любую партию по таким правилам, затем определить в ней победителя и записать ее в соответствующее окно. Однако в отличие от подобной задачи 13 такую партию не всегда можно будет легко переделать так, чтобы изменился победитель, поэтому подумать ребятам все-таки придется. Один из вариантов решения – игровой: поиграть с соседом в подобную игру и экспериментальным путем составить партии. Этот вариант также хорош для тех ребят, которые любят составлять «честные» партии, в которых игроки не поддаются друг другу.

Другой вариант решения – метод перебора. Лучше всего начать такой перебор по первому ходу Первого и закончить его, как только найдутся две подходящие партии. Проще исследовать партии, где Первый берет сразу несколько камешков, например, 4. Тогда на втором ходу выигрывает Второй, цепочку получившейся партии можно записать во второе окно. Если Первый берет на первом ходу 3 камешка, то дальше игра также идет без вариантов и выигрывает Первый.

Задача 30. Сложность этой задачи в том, что ребятам необходимо учесть одновременно два условия. С одной стороны, выиграть должен Первый, с другой стороны, это должно произойти именно на седьмом ходу, поскольку длина цепочки задана. Хорошо, если ребята уже видят связи между длиной цепочки, числом ходов сделанных в партии и выигрышем определенного игрока. Действительно, в цепочке 8 позиций, значит, сделано 7 ходов, из них 4 крестика и 3 нолика. На последнем ходу, конечно, поставлен крестик. Как и в некоторых других задачах, здесь можно двигаться как от начала цепочки к концу, так и наоборот. Двигаясь с конца, ребята просто расставляют 4 крестика и 3 нолика в заключительной позиции так, чтобы было 3 крестика в ряд и не было других рядов из трех одинаковых значков (как крестиков, так и ноликов), а затем убирают по одному значку в соответствии с очередностью хода, но так, чтобы 3 крестика появились только на последнем ходу. Двигаться от начала здесь несколько сложнее, ведь придется постоянно следить, чтобы игра не закончилась раньше (или позже). Сложность подобной ситуации компенсируется лишь тем, что здесь Второй может подыгрывать Первому: поддаваться или просто плохо играть, не замечая своих выгодных ходов. Естественно ребятам, которые хотят во что бы то ни стало построить «честную» партию (в которой оба игрока стремятся выиграть), мешать не надо, но им будет несколько сложнее.

Задача 31. Необязательная. Во второй части курса («Информатике 3 – 4») таких задач было довольно много. В третьей части задача на поиск русского слова с таким же мешком букв встречается впервые, поэтому напомним особенности подобных задач. Эти задачи находятся на стыке информатики и русского языка. При этом формальное информатическое (или математическое) решение, состоящее в полном переборе всех слов, имеющих такой мешок букв, детям осуществить будет пока довольно сложно. Так, из 5 разных букв (как в слове ОТСЕВ, например) можно составить 120 разных цепочек букв. Поэтому решая такие задачи, дети все-таки больше угадывают слова, чем по-настоящему перебирают. При этом они интуитивно используют некоторые лингвистические соображения, например, какие сочетания букв более популярны в языке, а какие, наоборот, можно сразу отбрасывать. Поэтому вы, скорее всего, столкнетесь с тем, что кто-то из детей довольно легко решает такие задачи. Это как раз те дети, у которых языковая интуиция развита хорошо. А у кого-то из ребят такие задачи не пойдут. При этом навести их на решение, не подсказав нужного слова, будет довольно затруднительно. Один из вариантов – все-таки предложить полный перебор, но подсказав первую букву искомого слова (тогда перебор существенно уменьшится). Для этого можно использовать дерево. В корневой вершине будет первая буква, в вершинах второго уровня – все возможные варианты второй буквы и т. д. Решение таких задач перебором – пропедевтика темы «Дерево всех вариантов», которой дети будут заниматься немного позже. Другой вариант работы с подобной задачей – предложить подумать над ней дома или оставить ее на будущее. В любом случае такие задачи лучше предлагать по желанию, вполне допустимо, если ребенок решит ее частично (для каких-то слов).

Ответ:

ОТСЕВ – СОВЕТ
ТЯПКА – ПЯТКА
АДРЕС – СРЕДА
СМОЛА – МАСЛО

Задача 32. Здесь ребята вспоминают особенности работы с конструкцией повторения. Если кто-то запутался, посоветуйте ему отмечать, сколько раз выполнены внутренние команды каждой конструкции повторения, ставя пометку около соответствующей конструкции, каждый раз доходя до слова КОНЕЦ. Также можно попросить ребят в этой задаче ставить пометку на поле после выполнения каждой конструкции повторения. Тогда в случае ошибки вы сможете понять, при выполнении какой части программы она допущена. При правильном решении положение Робика на поле после выполнения программы совпадает с положением в начальной позиции.

Ответ: позиция после выполнения программы Ю.

Задача 33. Необязательная. Задача имеет много разных решений, но именно от этого многообразия ребенок и может растеряться. Первый вопрос – с какого условия начать. Наиболее конкретную информацию дает последнее утверждение, ставим пятой бусиной вопросительный знак. Теперь поищем другие утверждения, связанные с вопросительным знаком, их два: третье и предпоследнее. Ставим точку в любое окно, идущее раньше вопросительного знака, а тире – в любое окно, идущее позже. У нас есть утверждение, связанное с точкой, читаем его и ставим закрывающуюся скобку позже точки. Куда бы мы до этого ни поставили точку, место для закрывающейся скобки можно найти всегда. Оставшиеся утверждения никак не связаны с уже поставленными знаками, они не задают конкретных мест для оставшихся знаков, а говорят лишь о порядке между ними. Эти утверждения указывают на то, что двоеточие идет из оставшихся знаков позже всех, поэтому ставим его в последнем свободном окне, три оставшихся знака расставляем как угодно.

Компьютерный урок «Игра ползунок», задачи 29 – 35

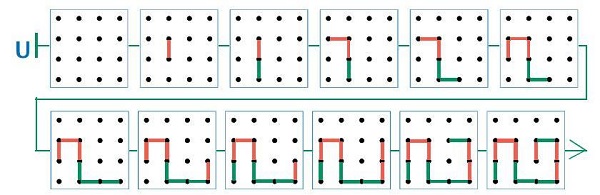
Задача 29. Задача на понимание правил игры ползунок. Для решения этой задачи будут очень полезны примеры с листа определений учебника (с. 18) ― какие ходы в этой игре разрешены, а какие нет. Ломаная на поле должна быть незамкнутой, без самопересечений, ее соседние отрезки могут располагаться либо под прямым углом, либо находиться на одной прямой. И (что важно помнить при решении этой задачи) ломаная на поле может быть только одна. Исходя из этих соображений, в данной задаче ребята и достраивают ходы Второго – они достраиваются однозначно. После того как партия достроена, можно определить победителя: выиграл тот из игроков, кто нарисовал последний отрезок. Но по виду ломаной это не всегда можно выяснить. В таком случае победителя можно выявить, сосчитав количество отрезков каждого цвета. В данном случае красных отрезков будет на один больше, значит, игра закончилась после хода Первого – в игре выиграл Первый.

В этой задаче ребята проводят отрезки Второго инструментом «карандаш». Скорее всего, отрезки не будут получаться у ребят идеально ровными, но это не страшно. Как обычно, любой неправильно проведённый ход можно стереть ластиком.

Задача 30. Ещё одна задача на усвоение правил игры ползунок. Наиболее простой способ решения этой задачи – сыграть с товарищем партию в ползунок на бумаге, а затем перенести заключительную позицию на экран. По окончании игры стоит попросить ребят провести проверку выполнения правил игры.

Задача 31. Задача, аналогичная компьютерной задаче 9. Как и в задаче 9, позиции можно расставить в цепочке и просто формально, ориентируясь только на число звеньев ползунка.

Задача 32. Аналогичную задачу ребята уже решали (см. комментарий к компьютерной задаче 10). Как и в задаче 10, здесь лучше всего начать строить цепочку с конца, начиная с заключительной позиции.

Задача 33. На первый взгляд эта задача может показаться не очень лёгкой, потому что придётся сопоставлять 4 утверждения и принимать во внимание, какие фигурки даны в библиотеке. Однако ситуация быстро прояснится, если учитывать условия утверждений в правильном порядке. Итак, все фигурки у нас разные, причём все бусины первого уровня — бабочки. В библиотеке всего две бабочки, значит на первом уровне дерева будут расположены либо две, либо одна бабочка. В нашем дереве должно быть три уровня вершин, и все рыбы ― листья. В дереве должно быть три уровня бусин, значит, по крайней мере одна фигурка на втором уровне не должна быть листом, а значит должна быть не рыбой, а бабочкой. Остальных рыб можно разместить как угодно на втором и третьем уровнях дерева, все они при этом должны быть листьями.

Задача 34. Аналогичные задачи ребятам уже встречались в прошлом учебном году. Решение здесь однозначное: недостающие в первой конструкции повторения команды «вправо—вверх—вверх», во второй — «вниз—вниз—вправо». Каждую конструкцию нужно повторить 3 раза.

Задача 35. Здесь на слова цепочки партии игры накладываются жесткие требования: все слова должны начинаться с согласной (а значит, все, кроме последнего, должны и заканчиваться на согласую) и должны быть длины 5. Если у ребят с этой задачей возникнут проблемы, можно решать её коллективно или по группам. Соберите вокруг себя всех ребят, которые не могут построить нужную цепочку, и попросите их для начала назвать как можно больше слов из пяти букв, которые начинаются и заканчиваются на согласную. После того как слов окажется больше 20, можно начинать выстраивать из них цепочку игры. По ходу этого построения можно придумывать слова-связки, которых недостаёт для соединения кусочков цепочки между собой. Вот пример подходящей цепочки: ЛЕСОК – КОВЁР – РОЖОК – КОТЁЛ – ЛАРЕЦ – ЦЫГАН – НАГАН – НИТКА.