Информатика. 3–4 класс (часть 3) Демо+методичка

Проект «Турниры и соревнования», 2 часть

Описание проекта

Во второй части курса («Информатике 3 – 4») состоялось первое знакомство ребят с круговым и кубковым турниром. Тогда детям предлагалась серия задач, посвященная правилам проведения турниров, подсчету очков и турнирной таблице. В качестве дополнительного задания (продолжения проекта) ребятам предлагалось провести турниры в классе, но вряд ли кто-то успел это сделать в рамках 1 часа, отведенного на проект. В третьей части курса («Информатике 4») мы предлагаем провести турниры в классе в обязательном порядке (в этом собственно и заключается данный проект).

Значительная часть материала учебника посвящена играм. В частности, в учебнике имеется большая серия задач на проведение турниров в группах по ходу изучения различных игр. Поэтому детям полезно в начале вспомнить правила проведения турниров и подсчета очков. В учебнике дети будут в основном знакомиться с играми с полной информацией, где от участников требуется следовать некоторой стратегии или хотя бы думать, делая ходы. В этом проекте мы, напротив, хотим, чтобы дети сосредоточились не на ходе игры, а на процессе проведения турнира. Поэтому советуем выбрать для проведения турнира совсем простую игру. Хорошо подойдет игра, где результат зависит от удачи, поэтому думать от игроков не требуется. Ну и конечно, в этом проекте нужно выбирать игры, в которые играют парами. Например, можно по очереди бросать кости (или обычный кубик), выигрывает тот, у кого выпало больше очков. Можно по очереди вытягивать карты из колоды, выигрывает тот, у кого старше карта (о старшинстве карт нужно заранее договориться со всем классом). Можно крутить волчок на поле, где по кругу размещены числа (по типу рулетки) и т. д. С точки зрения упрощения проведения кубкового турнира лучше выбирать такие игры, в которых невозможно или маловероятна ничья, либо заранее обговорить действия игроков по определению победителя в случае ничейной позиции в игре. Так в случае бросания костей можно договориться, что если у двух игроков выпало одинаковое число очков, они будут бросать кости до тех пор, пока число очков не станет разным.

Учителю нужно заранее для себя решить следующий вопрос – проводить этот проект всем классом или в подгруппе. С одной стороны, для ребят может оказаться важным определить победителя во всем классе. С другой стороны, чем больше число участников, тем сложнее организовать турнир, поэтому в подгруппе учителю будет работать проще. Мы предлагаем описание этого проекта для обоих случаев.

Проведение кубкового турнира

В первой части проекта проводится кубковый турнир в классе (или подгруппе) по игре «Кости» (или другой, которую вы выбрали). По правилам кубкового турнира участники турнира разбиваются на пары и играют друг с другом. Проигравшие выбывают из дальнейших соревнований, а победители делятся на пары и снова играют друг с другом и так до тех пор, пока не останется ровно один участник. Он и будет победителем турнира. Этот процесс можно изобразить в виде дерева. Листья такого дерева – все ученики своей первой по счету игры. Поскольку каждый ученик класса должен участвовать хотя бы в одной партии, то у дерева листьев должно быть столько, сколько человек участвует в турнире. Проще всего дерево будет выглядеть, если число участников турнира равно степени двойки (два, четыре, восемь и т. д.). У нас это будет 32 участника (если турнир проходит всем классом) или 16 участников (если турнир проходит в подгруппе). Все листья такого дереве расположены на последнем уровне и поэтому можно начать турнир одновременно со всем классом и дальше каждый тур турнира можно проводить одновременно со всеми оставшимися участниками. Чтобы получить такое дерево достаточно взять заготовки деревьев на страницах 14 – 15 или 16 – 17 и правильно соединить вершины трех последних уровней.

Если число участников турнира не равно степени двойки, то часть учеников начинает турнир в первом туре, а остальные присоединяются к ним во втором туре, играя друг с другом или с победителями первого тура. Это немного несправедливо с точки зрения игры, но учитывая случайность победы, это не столь важно. В этом проекте важно, чтобы каждый ученик поучаствовал хотя бы в одной партии турнира и чтобы он мог изобразить ход турнира в виде дерева. Чтобы не запутаться, советуем вам предварительно составить дерево турнира. Получить дерево для вашего числа участников можно также из заготовки на страницах 14 – 15 или из заготовки на страницах 16 – 17. Для этого, несколько пар участников нужно убрать с последнего уровня и поставить вместо каждой из них одного участника на предпоследний уровень. Пусть n – число участников турнира (большее 16, но меньшее 32). Тогда на заготовке дерева на стр. 14 – 15 нужно на последнем уровне зачеркнуть (32 – n) пар листьев, а на предпоследнем уровне (32 – n) вершин сделать листьями. В таком случае на предпоследнем уровне оказывается ровно 16 вершин-учеников, которые делятся на пары, играют между собой, после чего остается 8 учеников и т. д. Первые 4 уровня вершин на заготовке дерева уже прорисованы.

Вот пример такого дерева для 25 участников турнира.

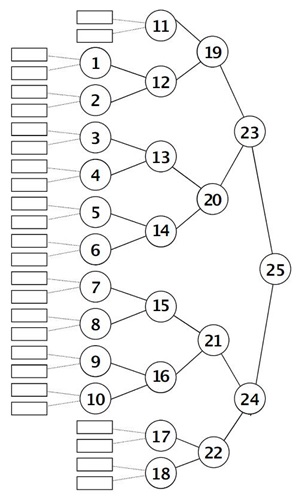
По ходу проведения турнира все дети в обязательном порядке должны построить дерево турнира. После того как структура дерева до конца прояснилась, в вершины-листья вписываются все участники турнира. Чтобы не было споров можно сделать это просто по алфавиту сверху вниз и по уровням слева направо. То есть в самой верхней (не зачеркнутой) вершине последнего уровня будет самый первый по списку ученик, за ним следующие по списку. Как только вершины на последнем уровне кончились, нужно распределить их парами и соединить каждую пару с вершиной предпоследнего уровня. Оставшиеся свободными вершины предпоследнего уровня надо пометить как листья. Следующий по списку ученик записывается в верхний лист предпоследнего уровня. Ниже записываются все следующие по списку ученики. В соответствии с получившимся деревом все ученики разбиваются на пары и начинается турнир. Чтобы не запутаться, лучше проводить турнир по турам, которые будут соответствовать уровням дерева. Партии не должны проводиться слишком быстро, чтобы все дети успели записать участников и результаты всех игр в дерево. По окончании первого тура каждая пара должна сообщить всему классу результат игры – фамилию победителя, которую дети должны записать на предпоследнем уровне перед соответствующей парой. После того как все вершины предпоследнего уровня окажутся заполненными, начинается второй тур. По ходу турнира все больше ребят становятся зрителями (они уже не участвуют в играх), которые только фиксируют результаты партий. Наконец, определяется победитель турнира. Заметим, что кубковый турнир практически не требует какого-то отдельного подсчета очков и подведения итогов, поэтому для оформления его результатов ничего кроме дерева не потребуется.

Проведение кругового турнира

Круговой турнир занимает значительно больше времени, чем кубковый. Так, круговой турнир с 32 участниками будет включать в себя 496 партий (а кубковый только 31 партию). Сэкономить время можно, если проводить турнир в два этапа. Поэтому вам нужно сразу определиться, сколько этапов (один или два) будет включать турнир. Так на целом классе мы бы рекомендовали проводить турнир в два этапа, а в подгруппе можно проводить турнир в один этап (но окончательный выбор, конечно, остается за вами.

Турнир в один этап

По правилам кругового турнира каждый участник в группе должен сыграть с каждым. Если круговой турнир проводится в один этап, группа состоит из всех учеников, присутствующих на уроке. В процессе проведения такого турнира каждый ученик должен поучаствовать в турнире и заполнить общую турнирную таблицу, включая и распределение мест. Для начала дети должны найти и подготовить к работе подходящую турнирную таблицу. Если турнир проводится на всем классе (участников от 17 до 32), нужно взять таблицу на страницах 18 – 19, а если на подгруппе (участников меньше 17), нужно взять таблицу на странице 20. В этой таблице нужно ограничить жирными линиями часть таблицы, которая понадобится для работы (рассчитанную на ваше число участников). Затем в шапке выделенной таблицы по горизонтали и вертикали нужно написать фамилии всех участников турнира, чтобы дети не запутались, лучше предложить им сделать это в алфавитном порядке.

Проведение турнира

Теперь каждый участник турнира берет свою таблицу и начинает играть по очереди с каждым из остальных участников турнира, по ходу заполняя свою строку в таблице, записывая в каждой клетке очки, которые он набрал в соответствующей партии. Поскольку в этом проекте мы предлагали использовать игры, в которых не бывает ничьих, за победу ученик будет ставить себе в соответствующей клетке 1 очко, за поражение – 0 очков. Лучше если оба играющих партию будут контролировать друг друга во время заполнения таблицы, иначе потом все ошибки в таблице найти будет сложно.

Проще всего организовать турнир, разделив сначала всех учеников пополам – одна часть сидит за партами, а другая – перемещается по кругу, играя партию с каждым из сидящих учеников. После того как пройден полный круг, нужно каждую половину учеников снова разделить пополам и опять обойти круг. После этого у каждого из детей останется совсем не много несыгранных партий и дети могут просто перемещаться по классу и играть с теми, с кем они еще не играли.

Обмен результатами партий

В некоторый момент у каждого ученика его строка в турнирной таблице окажется заполненной и нужно будет организовать обмен результатами партий. Для этого ученики по очереди могут выходить к доске и выписывать свою строку в таблице. После того как у всех учеников таблица окажется заполненной, нужно проверить правильность заполнения таблицы. Правильно заполненная таблица должна быть «обратно симметричной» относительно диагонального ряда из левого верхнего угла. Это значит, что если в клетке на пересечении строки а и столбца в стоит «1», значит в клетке на пересечении строки в и столбца а должно стоять «0» и наоборот.

Подведение итогов

После того как у всех учащихся в таблицах окажутся результаты всех партий, ребята начинают подсчитывать для каждого участника число очков, а затем расставлять места. Если при этом у двух учащихся число очков одинаковое, то выше место у того, кто победил в партии между ними. Однако может оказаться так, что сразу у нескольких учеников число очков одинаковое. Поэтому с детьми надо договориться заранее, как в таких случаях поступать. Вот несколько вариантов развития событий в таком случае:

• Всем ученикам с одним и тем же числом очков присудить одинаковое место. Это самый легкий вариант, но при таком варианте детям может показаться неестественным, что в классе, например, три первых места.
• Собрать всех учеников, набравших одинаковое число очков в одну группу. Вычленить из общего числа очков каждого члена группы очки, набранные в играх с участниками группы и распределить места членов группы в порядке убывания этих очков. Если и после этого в классе найдутся группы больше двух ребят с одинаковым числом очков, в таких группах можно провести дополнительные партии.

Турнир в два этапа

При проведении турнира в два этапа всех учащихся нужно разделить на 4 группы. Сначала круговые турниры проводятся в группах. При этом каждый член группы должен сыграть по одной партии с каждым членом своей группы. Для этого следует использовать турнирную таблицу на странице 21 (если в каждой группе больше 4 человек) или на странице 20 (если в группах меньше 5 человек). Проведение такого турнира в каждой группе будет проходить по той же схеме, что и турнир в одни этап (см. выше). После того как в каждой группе определился победитель, четверо победителей в группах играют круговой турнир между собой, используя турнирную таблицу со страницы 17. Турнирную таблицу этого турнира заполняют все, вне зависимости от того, играли ли они в этом турнире или нет.

Дополнительно

Довольно интересно строить турнирные деревья по таблице. В таблице имеются результаты игр каждого с каждым. Можно случайным образом расставить учеников в листья таблицы турниров и выявить победителя, не проводя реальных игр, а списывая результаты игр из турнирной таблицы. Потом расставить учеников иначе и снова попробовать выявить победителя. Если победитель кругового турнира не выиграл у всех своих конкурентов, то всегда можно так расставить учеников, что победитель кругового турнира вылетит из кубкового турнира уже на первом этапе. При проведении реального турнира результат, скорее всего, будет другим. Почему?

Обсудите с детьми, в чем состоит сходство выявления первого (победителя) в кубковом турнире с определением первого элемента в множестве методом пузырькового всплытия (см. проект «Сортировка», мини-проект 5). Принцип определения первого в обоих случаях одинаков, только в множестве чисел всегда 15 больше 9, слово ВОРОТА всегда в алфавитном порядке идет раньше слова МОЛОКО, а вот в футбол сборная России выигрывает у сборной Франции не всегда. В играх, как правило, результат заранее не известен. Иначе зачем проводить соревнования?