Информатика. 3–4 класс (часть 2) Демо+методичка

Уроки 27–28. Склеивание мешков цепочек

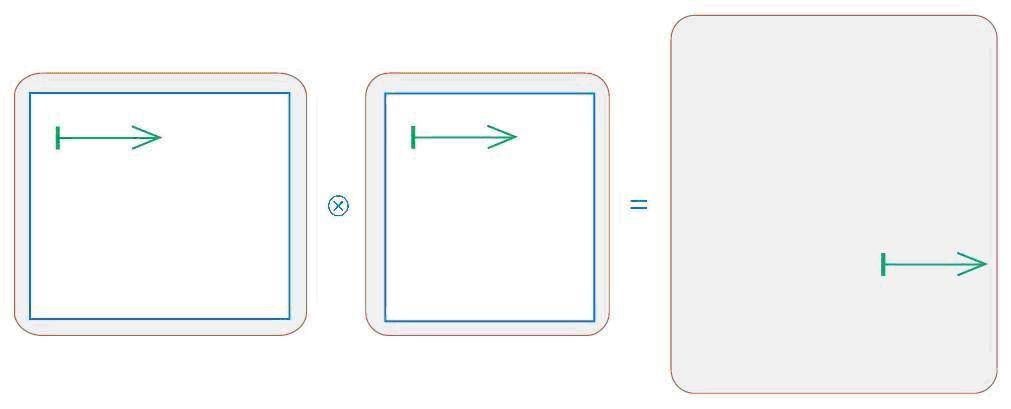
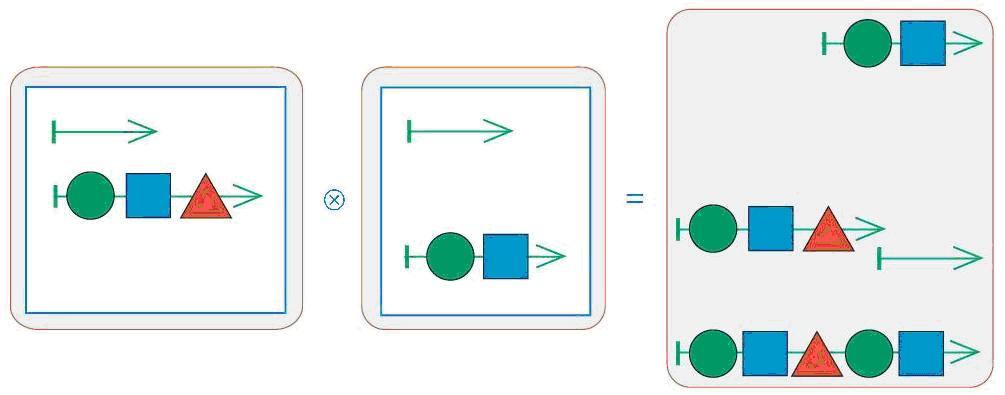
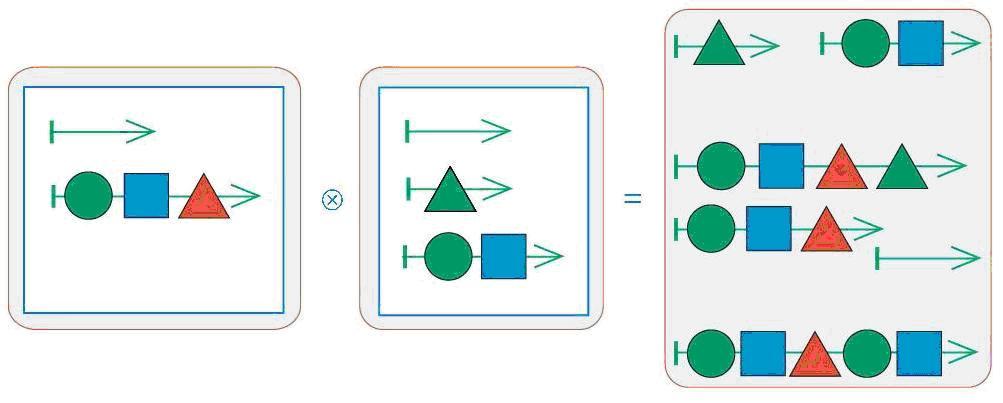
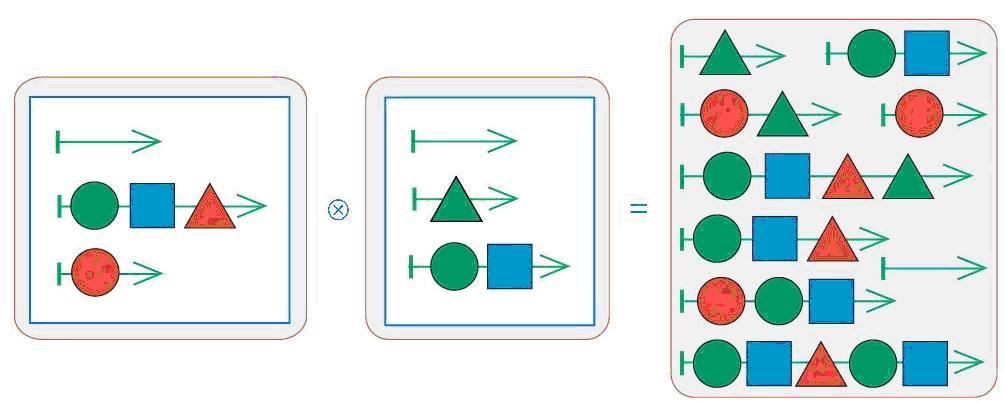
Дети уже знакомились в курсе с операцией над цепочками. Теперь им предстоит освоить еще одно действие, но теперь уже над мешками цепочек. Как видно из листа определений, в результате склеивания двух мешков цепочек получается снова мешок цепочек. В нем лежат все такие цепочки, начало которых – это цепочка из первого мешка, а конец – цепочка из второго мешка. Из этого следует сразу несколько важных свойств (отраженных на листе определений). Операция склеивания мешков не обладает переместительным свойством, т. е. от перемены мест аргументов результат меняется. Во многом (кроме переместительного свойства) эта операция напоминает умножение. Первое сходство – количество цепочек в мешке-результате. Нетрудно догадаться, что для подсчета достаточно перемножить число цепочек в первом и втором мешках. Второе сходство – наличие элементов, поведение которых сходно с поведением нуля и единицы при умножении. Пустой мешок при склеивании с любым мешком дает пустой мешок ровно также как ноль при умножении на любое число дает ноль. Мешок с одной пустой цепочкой в нем при склеивании с любым мешком дает тот же самый мешок, как единица при умножении на любое число дает то же число.

Операция склеивания мешков имеет комбинаторный характер: чтобы правильно ее выполнить, нужно построить все пары из цепочек первого мешка и цепочек второго мешка. Чтобы не забыть никаких цепочек и не написать лишних, удобно использовать дерево, таблицу или некоторую стратегию, позволяющую не сбиваться. Вот один из таких способов. Берем одну цепочку первого мешка (ставим около нее галочку) и начинаем по очереди приклеивать к ней цепочки второго мешка, перебирая их сверху вниз. Как только очередная цепочка второго мешка использована, ставим около нее галочку. Когда мы добрались до конца второго мешка и около каждой его цепочки стоит по одной галочке, берем вторую цепочку первого мешка и снова склеиваем ее с каждой цепочкой второго мешка и т. д. Нетрудно заметить, что процесс склеивания мешков напоминает процесс умножения многочлена на многочлен.

 

Решение задач из учебника

Задача 155. Для решения этой задачи достаточно понимания материала листа определений. Если кто-то из слабых детей запутался, можно предложить пользоваться пометками при переборе цепочек при склеивании, как описано выше.

Задача 156. Детям будет проще склеивать мешки слов, поскольку в результате получается мешок с осмысленными словами (по крайней мере, некоторыми). Так в первом примере на склеивание в мешке-результате получаются два русских слова (МАМА, ПАПА) и две бессмысленных с точки зрения русского языка цепочки букв (МАПА, ПАМА).

Во втором и третьем примерах наличие пустой цепочки в мешках может привести к потере цепочек в мешке-результате. Если кто-то из ребят допустит такую ошибку, вам снова поможет обсуждение с детьми использования пометок при переборе. Другой вариант – вернуть ребенка ко второму и третьему примерам на листе определений – там обсуждаются аналогичные случаи склеивания.

Задача 157. Как и в двух предыдущих задачах, здесь детям достаточно будет использовать информацию листа определений и быть внимательными. В третьем примере получается пустой мешок (как показано на листе определений). Во втором примере столько пустых цепочек, что кто-то наверняка запутается и потеряет часть решения. Это хороший повод поговорить о дополнительных способах проверки в задачах на склеивание мешков цепочек. К этому моменту дети уже имеют некоторый опыт выполнения этой новой операции, и сообразительные дети, скорее всего, готовы сделать из него некоторые выводы. Первый вывод должен касаться числа цепочек в мешке-результате. Так видно, что в большинстве примеров листа определений в каждом из двух мешков по две цепочки, а в мешке-результате их четыре. Это позволяет сделать первый вывод – количество цепочек в мешке-результате не зависит от того, какие именно цепочки лежат в мешках, а зависит только от их количества. Кто-то из детей может сказать, что количество цепочек в мешках-аргументах перемножается, кто-то – что складывается (для двух мешков из двух цепочек в обоих случаях получается четыре). Это легко проверить, используя другие примеры – где цепочек в мешках 2 и 3 или где цепочек в мешках 2 и 0. Так дети приходят к выводу, который позволяет выполнить первую (самую грубую) проверку в задачах на склеивание: если число цепочек в мешке не совпадает с предполагаемым, значит, в решении где-то есть ошибка. Если число цепочек правильное, это необязательно означает, что решение верное, просто здесь нужна уже более тонкая проверка. Например, хорошо подойдет парная проверка, в ходе которой ребята не меняются тетрадями, а просто показывают друг другу свои мешки-результаты и помечают все общие цепочки. Это позволяет локализовать ошибки и обсудить их.

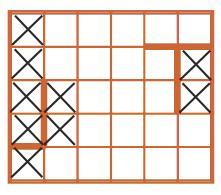
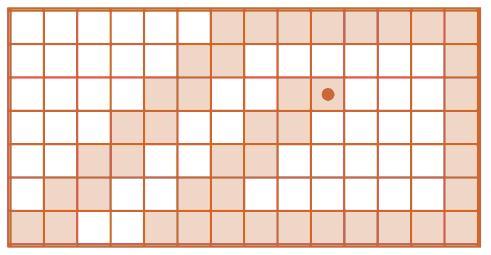
Задача 158. Необязательная. Это первая задача из новой серии задач про Робика. Даны только форма поля и программа, все остальное придется выяснить ребятам самим. Главный вопрос – где находился Робик в начальной позиции. Из условия задачи не ясно, сколько здесь возможных решений – одно или много. Эту задачу можно решать методом проб и ошибок: перебирать все возможные квадратики поля и ставить в них Робика в начальной позиции. Однако, как мы это неоднократно обсуждали, ценность метода проб и ошибок не только в том, что он позволяет случайно набрести на решение. Часто в ходе поиска человек накапливает опыт, начинает понимать, как все устроено. Кто-то, сделав несколько первых попыток, может понять, что из некоторых квадратов нельзя выполнить даже первую команду, почему ее выполнить нельзя и где находятся такие заведомо неподходящие клетки. Это наблюдение можно обобщить на два первых хода и т. д. Такие неподходящие квадратики надо каким-то образом помечать, но не так, как Робик закрашивает квадратики. Например, вычеркивая крест-накрест те клетки, из которых нельзя выполнить первую команду влево, получаем

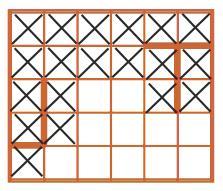
Последовательно добавляя каждую следующую команду, вычеркиваем все новые и новые клетки. Так, вторая команда – вправо – никакой новой информации не дает (никаких новых клеток вычеркнуть нельзя). Дальше Робик должен выполнить две команды вверх. Значит, он не может начинать свой путь ни в одной из клеток двух верхних рядов поля и двух первых клеток под горизонтальными стенками поля. Получаем такой рисунок:

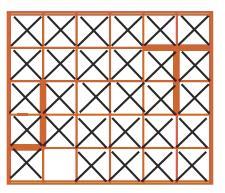
При решении задачи могут появиться новые обобщающие идеи. Например, можно заметить, что Робик, выполнив почти всю программу (кроме последней команды), выполнил лишь одну команду влево, но пять раз выполнил команду вправо. Поэтому можно зачеркнуть и еще клетки (все клетки четырех правых столбцов поля):

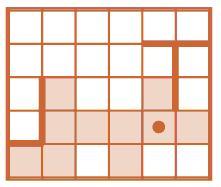
Остается одна незачеркнутая клетка; пробуем выполнить программу, начиная из этой клетки – все получилось (приводим на рисунке позицию после выполнения программы Щ):

Такая модификация метода проб и ошибок подразумевает существенный элемент прогнозирования, забегания вперед. Если этот метод будет трудным для ребят, можно предложить им другой подход – решение с конца. Он заключается в том, чтобы выполнить программу на листе клетчатой бумаги (на поле без границ) и получить рисунок закрашенных Робиком клеток. Теперь останется найти возможное положение этого рисунка на поле, данном в задаче. Это не просто и потребует других мыслительных навыков, скорее геометрических – необходимо учесть расположение не только границ поля, но и стенок внутри поля.

Задача 159. В формулировке задания имеется отрицание: «…нет мешка с двумя одинаковыми бусинами». Это вызовет дополнительные трудности при решении. Главное не спешить, все аккуратно отмечать и время от времени снова читать условие задачи.

Рекомендуем поставить прямо в задании рядом с каждым словом «мешок» пометку – внутренний или внешний. Получаем фразу: «Найди такой мешок (внешний), в котором нет мешка (внутреннего) с двумя одинаковыми бусинами». Проверяем выполнимость этого утверждения для каждого мешка. В мешке К есть мешок (второй) с двумя одинаковыми бусинами – значит, он не подходит. Аналогично проверяем утверждение для мешка Л. Убеждаемся, что в его третьем внутреннем мешке есть две одинаковые бусины; значит, он тоже не подходит. Продолжая перебор, выясняем, что условию удовлетворяет мешок М. Но нужно просмотреть и мешок Н – проверить, что он не удовлетворяет условию.

Задачи 160 и 161. Материал для этих примеров на склеивание мешков цепочек взят из курса русского языка. Однако склеивание мешков, как и во всех предыдущих задачах, выполняется формально, на основании листа определения. В отличие от предыдущих задач в мешках-результатах цепочек будет довольно много (в каждой из задач их будет 18). Еще одно отличие состоит в том, что в мешках-результатах окажутся среди прочих и одинаковые слова. Аналогичная ситуация пока встречалась детям лишь раз, причем тогда одинаковые цепочки были пустыми (см. задачу 157, второй пример). При решении задач 160 и 161 можно поговорить с ребятами о том, в каком случае в мешке-результате оказываются пустые цепочки, а в каком –  нет. Для ответа на этот вопрос ребятам можно предложить просмотреть все выполненные примеры на склеивание (как на листе определений, так и в задачах). При этом можно заметить важное отличие данных примеров – здесь во втором мешке лежат одинаковые цепочки. С точки зрения русского языка этот факт имеет простое объяснение: во втором мешке лежат окончания существительных для всех падежей, и эти окончания для разных падежей могут совпадать. В результате общего обсуждения ребята приходят к выводу: только в случае наличия в одном из мешков одинаковых цепочек в мешке-результате могут появиться одинаковые цепочки. Этот факт, как и вывод, приведенный в комментарии к задаче 157, можно использовать для первичной проверки правильности склеивания мешков.

Задача 162. Эта задача трудная. Во-первых, в ней есть толкования, похожие на толкования из словаря (второе и третье). На самом деле они означают совсем не то, что словарные (и они ложны), но чтобы в этом убедиться, нужно внимательно их прочитать от начала и до конца. Во-вторых, четвертое толкование является неполным по сравнению со словарным (но тем не менее, истинным). Такие ситуации обсуждались в комментариях к задачам 134 и 150.

Задача 163. Необязательная. Тем, у кого дело сразу не пойдет, посоветуйте сначала понять, где Робик мог стоять вначале, до выполнения программы. Ученик, скорее всего, быстро сообразит, что Робик должен находиться на одной из раскрашенных клеток и иметь возможность дважды сдвинуться вниз (это любая из трех «верхушек» буквы Ш). Остается только найти, какая именно «верхушка» подходит.

Ответ: пропущенные команды: влево, вверх, влево, вверх.

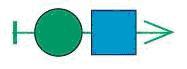
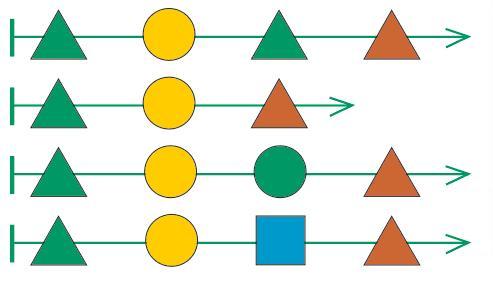
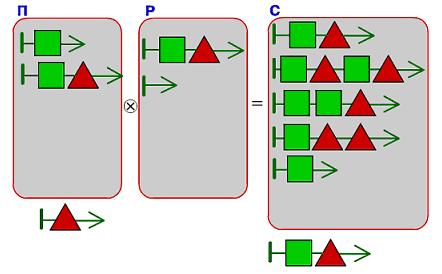
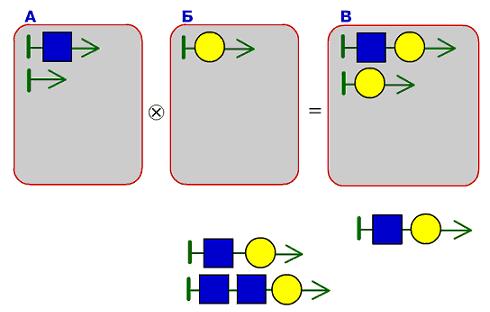
Задача 164. В этой задаче ребятам впервые предстоит выполнить операцию, обратную склеиванию мешков цепочек (условно можно называть ее разрезанием мешка цепочек). Очень хорошо, если к этому моменту ребята усвоили основные закономерности склеивания мешков цепочек. Так, в первом примере в мешке-результате лежит 6 разных цепочек, а первом мешке-аргументе – 3 цепочки. Значит, во втором мешке-аргументе должны лежать 2 разные цепочки. Также нетрудно по длине цепочек в мешках догадаться, что длина цепочек во втором мешке-аргументе не больше чем 2. Решение можно начинать и строить по-разному. Один из вариантов – начать строить цепочки мешка, ориентируясь на самую короткую цепочку в мешке-результате. Она имеет длину 2 и не совпадает ни с одной цепочкой длины 2 первого мешка, значит, она получилась в результате приклеивания к верхней цепочке первого мешка. Отсюда сразу следует, что одна из цепочек второго мешка состоит из одной зеленой квадратной бусины. Теперь можно выделить в мешке-результате все цепочки, которые получились после приклеивания этой цепочки к цепочкам первого мешка. Из оставшихся цепочек можно снова выделить самую короткую, которая получается в результате приклеивания к верхней цепочке первого мешка, и т. д.

Задача 165. Необязательная. Рисунок Робика состоит из пяти непересекающихся узоров, каждый из которых соответствует определенной конструкции повторения. Поэтому, проходя по классу, вы всегда сможете определить, в какой конструкции (или двух соседних) ученик допустил ошибку. В таком случае можно попросить его взять чистое поле с листа вырезания и выполнить программу еще раз.

Ответ:

Задача 166. В случае затруднения предложите начать с какого-нибудь одного слова, например со слова ДЫМ.
Правильных ответов здесь много, поскольку на дерево букв не накладывается никаких условий кроме того, что мешок его путей должен совпадать с мешком U. Конфигурация такого дерева может быть самая разная, в частности, подойдет и дерево, имеющее 9 корневых букв Д, где каждое слово расположено на отдельной «ветке». В таком случае дерево будет иметь 33 вершины.

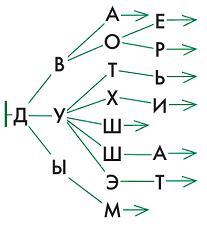
Кто-то захочет сэкономить, нарисовав на каждом уровне вместо нескольких одинаковых вершин одну, как на деревьях на листах определений. Самое экономное дерево будет иметь 18 вершин:

Обратите внимание, что на букве Ш нельзя сэкономить, придется поставить ее на третьем уровне дважды, поскольку в одном пути она является листом, а в другом пути имеет следующую букву.

Задача 167. В этой задаче склеивание мешков уже частично выполнено, надо вписать в мешок лишь недостающие слова. Для кого-то это может оказаться не так уж просто, учитывая наличие во втором мешке одинаковых цепочек. В случае затруднения посоветуйте учащемуся выполнить склеивание самому, а затем сравнить результат склеивания с мешком-результатом в задаче.

Задача 168. Это несколько более сложная задача на разрезание, чем задача 164. Для начала попробуем найти в мешке-результате все цепочки, начальный участок которых совпадает с данной цепочкой из первого мешка: они получились в результате приклеивания всех цепочек второго мешка к этой цепочке первого мешка. Так отыскиваются три цепочки, и они позволяют найти сразу все цепочки второго мешка. Одна из них – данная, вторая – пустая, а третья состоит из зеленой круглой и синей треугольной бусин. Теперь найдем в мешке-результате все цепочки, которые получились после приклеивания ко всем цепочкам первого мешка первой цепочки второго мешка (их конечный участок совпадает с первой цепочкой второго мешка). Таких оказывается две, значит, в первом мешке две цепочки: одна из них – данная, а вторая состоит из двух бусин – красной квадратной и синей треугольной. Теперь остается проверить, что при склеивании получившихся мешков цепочек действительно получается мешок-результат.

Задача 169. Необязательная. Несложная задача на повторение порядка бусин в цепочке. По окончании решения можно предложить ребятам посмотреть в толковом словаре, что означает получившееся слово и попробовать это нарисовать.

Ответ: КАРАКАТИЦА.

Задача 170. Необязательная.

Ответ: первое и последнее утверждения истинны, остальные – ложны.

Задача 171. Задача на повторение словарного порядка. В данном случае все слова начинаются на ША, значит, упорядочение слов можно начать с деления слов на группы по третьей букве. Часть слов упорядочивается по этой букве, а оставшиеся слова начинаются на ШАР. Ясно, что первое слово в этой группе будет ШАР, а все остальные слова можно разделить на группы по четвертой букве. В результате по четвертой букве упорядочиваются почти все оставшиеся слова, кроме ШАРИК и ШАРИКОВЫЙ.

Задача 172. Необязательная.

Наиболее сложная задача курса на разрезание мешка цепочек, предназначенная в основном для сильных учащихся.
Это обратная задача на склеивание мешков. Для того чтобы правильно заполнить мешки, сначала сосчитаем количество цепочек в мешке-результате – их 9.  Значит, возможны два варианта решения: либо одна цепочка в одном мешке и 9 цепочек в другом, либо по 3 цепочки в каждом мешке. Так как начало цепочек в мешке-результате разное и концы цепочек разные, то первый вариант возможен только с пустой цепочкой в том мешке, где одна цепочка. Но в условии указано, что в каждом мешке должна быть хотя бы одна непустая цепочка, значит, этот вариант не годится, и мы ищем решение с тремя цепочками в каждом мешке-аргументе.

В мешке-результате имеется пустая цепочка, значит, в каждом мешке должно быть, по крайней мере, по одной пустой цепочке:

Осталось найти две пары цепочек: по две цепочки в каждом мешке-аргументе, два начала и два конца тех цепочек, которые есть в заданном мешке-результате. При этом, так как в каждом из мешков-аргументов есть по пустой цепочке, то в мешке-результате должны лежать копии обеих оставшихся цепочек из первого мешка и копии обеих оставшихся цепочек из второго мешка. Значит, нужные нам цепочки надо искать среди цепочек мешка-результата и, значит, все искомые нами цепочки непустые – иначе в мешке-результате  было бы больше одной пустой цепочки.

Рассмотрим самую длинную цепочку в мешке-результате:

Эта цепочка точно получилась склеиванием двух непустых цепочек, иначе в мешке были бы и более длинные цепочки. Склеиванием каких двух непустых цепочек она получилась?

        1.  Предположим, что первая цепочка была длины 1 – состояла только из круглой зеленой бусины.

Но такой цепочки нет в мешке-результате (см. предыдущий абзац – все исходные цепочки должны быть и в мешке-результате). Значит, наше предположение неверно.

        2.  Предположим, что первая цепочка  была длины 2:

Такая цепочка есть в мешке-результате. Проверим это вариант: если такая цепочка лежит в первом мешке, то четвертая сверху слева цепочка получилась приклеиванием к ней цепочки из одной красной треугольной бусины:

Но такой цепочки (из одной красной треугольной бусины) нет в мешке-результате. Значит, наше предположение неверно.

        3.   Осталось два варианта: первая цепочка имела длину 3:

или длину 4:

Могла ли первая цепочка быть длиной 3? В принципе да, такая цепочка есть в мешке-результате. А вот цепочки длины 4 в мешке нет, поэтому, скорее всего, нужный нам вариант – это цепочка длины 3.

И тогда во втором мешке аргументе будет цепочка из круглой зелёной и квадратной синей бусины:

Опираясь на этот вариант, начнем строить другие цепочки в мешках-аргументах.

Судя по третьей сверху слева цепочке, во втором мешке должна быть цепочка из одной зеленой треугольной бусины:

Рассматривая оставшиеся цепочки в мешке-результате, видим, что в первом мешке-аргументе не хватает всего одной цепочки из красной круглой бусины:

В каждом мешке теперь три цепочки. Осталось проверить, что при склеивании этих мешков получится заданный мешок-результат.

Задача 173. Несложная задача на повторение листа определений «Перед каждой бусиной. После каждой бусины». После выполнения инструкции все бусины в цепочке должны оказаться раскрашенными – в цепочке должно быть пять желтых, пять красных и три синих бусины.

Задача 174. Необязательная. Скорее всего, вы уже обсуждали с детьми вопрос о том, как сосчитать число цепочек в мешке-результате при склеивании двух мешков (для этого надо перемножить число цепочек в мешках-аргументах). В этом случае задачу можно предлагать практически всем учащимся. Если же этот вопрос в классе не обсуждался, самое время обсудить его здесь. Для организации общего обсуждения с детьми вам помогут комментарии к задаче 157.

Задача 175. В этой задаче встречаются сложные случаи, когда «бусина не одна» и «бусины нет». Например, для всех путей, выходящих из корневой желтой круглой бусины, утверждение не имеет смысла, поскольку в четырех верхних путях желтая круглая бусина не одна, а в остальных – нет красной треугольной. Если вы видите, что ученик выписывает какой-то из этих путей, остановите его и вспомните вместе соответствующие листы определений. Также важно, чтобы каждый ребенок просмотрел все пути дерева, ведь в задании говорится, что необходимо выписать все цепочки, удовлетворяющие условию. Если вы видите, что ребенок потерял часть решений, попросите его изучить дерево еще раз, помечая листья, ведущие в уже просмотренные  им пути. Скорее всего, в процессе этой работы ученик сам найдет ошибку.

Ответ:

Задача 176. Необязательная.

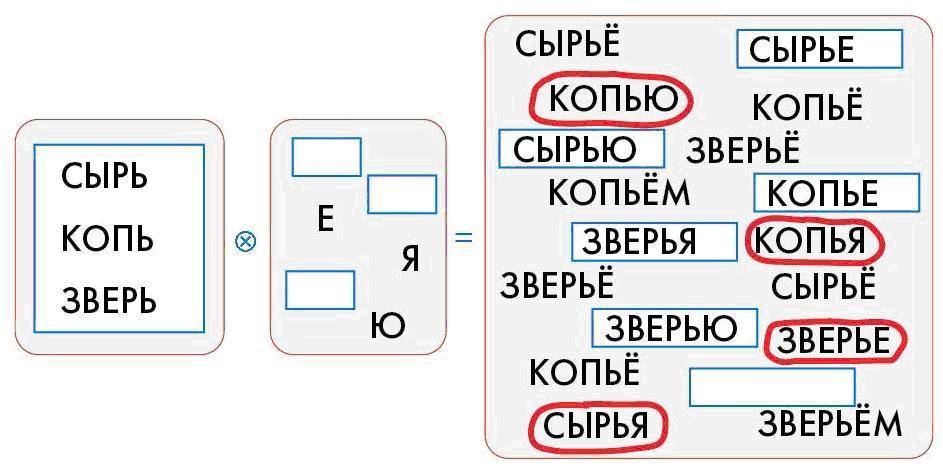
Очень интересная задача о склеивании мешков. Простой подсчет слов в мешке-результате (18 слов) и во втором мешке-аргументе (6 слов) говорит о том, что в первом мешке-аргументе  должно быть 3 слова.

Предположим, что слово ЗВЕРЬЕ получилось склеиванием ЗВЕРЬ-Е, слово КОПЬЮ – склеиванием КОПЬ-Ю, СЫРЬЯ – склеиванием СЫРЬ-Я. Вообще говоря, это не обязательно так, потому что некоторые слова в мешке-результате нам не известны, но пока сделаем такое предположение и попробуем решать задачу исходя из этого. Отсюда получаем все три слова в первом мешке: КОПЬ, СЫРЬ, ЗВЕРЬ. Отметим в мешке-результате те слова, которые получаются склеиванием известных частей из первого и второго мешков, запишем в окна те слова, которых не хватает в мешке-результате:

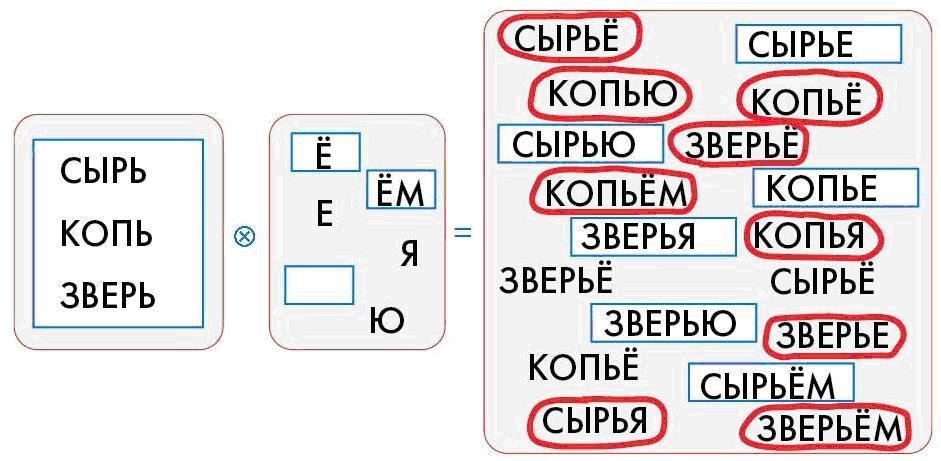
Теперь находим в мешке-результате слова, которые заканчиваются не теми словами, которые даны во втором мешке-аргументе: это Ё и ЁМ. Заполняем два окна во втором мешке, отмечаем слова, которые получаются склеиванием известных частей из первого и второго мешков:

Остается одно пустое окно во втором мешке и необведенные вторые экземпляры слов СЫРЬЁ, КОПЬЁ, ЗВЕРЬЁ в мешке-результате. Это означает, что во втором мешке есть два одинаковых слова Ё.

 

Вспомните, что мы в начале сделали предположение, и исходя из него получили решение. Наверное, если сделать другое предположение, можно получить и другое решение. Но проверять это слишком сложно и не обязательно – в этой задаче достаточно найти одно решение.

По окончании решения можно спросить детей, какие, с точки зрения курса русского языка, цепочки букв лежат в каждом из мешков. Оказывается, что в первом мешке лежат основы существительных русского языка, во втором мешке – окончания для всех падежей таких существительных, значит, в мешке-результате лежат все падежные окончания таких существительных среднего рода. 

Компьютерный урок  «Склеивание мешков цепочек», 1 часть, задачи 154 - 161

Задача 154. Задача не очень сложная, и здесь детям достаточно будет использовать информацию листа определений и быть внимательными. Это хороший повод поговорить о дополнительных способах проверки в задачах на склеивание мешков цепочек. К этому моменту дети уже имеют некоторый опыт выполнения этой новой операции, и сообразительные дети, скорее всего, готовы сделать из него некоторые выводы. Первый вывод должен касаться числа цепочек в мешке-результате. Так видно, что в большинстве примеров листа определений в каждом из двух мешков по две цепочки, а в мешке-результате их четыре. Это позволяет сделать первый вывод – количество цепочек в мешке-результате не зависит от того, какие именно цепочки лежат в мешках, а зависит только от их количества. Кто-то из детей может сказать, что количество цепочек в мешках-аргументах перемножается, кто-то – что складывается (для двух мешков из двух цепочек в обоих случаях получается четыре). Это легко проверить, так дети приходят к выводу, который позволяет выполнить первую (самую грубую) проверку в задачах на склеивание: если число цепочек в мешке не совпадает с предполагаемым, значит, в решении где-то есть ошибка. Если число цепочек правильное, это необязательно означает, что решение верное, просто здесь нужна уже более тонкая проверка. Например, хорошо подойдет парная проверка, в ходе которой ребята показывают друг другу свои мешки-результаты и замечают все общие цепочки. Это позволяет локализовать ошибки и обсудить их.

Задача 155. Это первая задача на склеивание цепочек букв. Детям такие задачи покажутся несложными, ведь в результате получаются осмысленные слова, которые можно быстро напечатать, а не перетаскивать бусины по одной, как с цепочками бусин. Для нас эти задания важны как связующие с курсом русского языка. Изучением частей слова занимается наука морфология. В примерах на склеивание мы тоже в основном стараемся составлять слово не из произвольных  частей, а осмысленно с точки зрения русского языка. Если у вас есть время и желание, на материале подобных задач можно сделать интегрированный урок «Русский язык – математика и информатика».

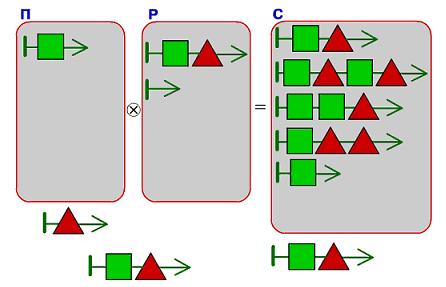
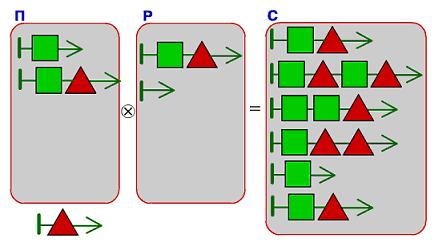
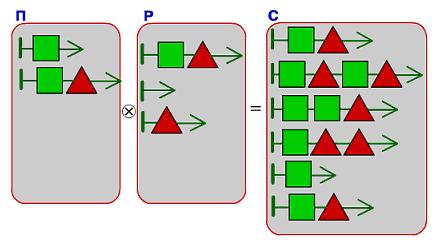
Задача 156. Это трудная задача на склеивание мешков цепочек – обратная задача. Для начала попробуем найти в мешке-результате цепочки, которые получились при склеивании цепочек, данных в мешках-аргументах: видим, что в мешок-результат нужно положить цепочку из одной зелёной квадратной бусины – кладём.

Первая цепочка в мешке-результате – такая же, как первая цепочка в мешке-аргументе Р. Это значит, что либо в мешке П должна лежать пустая цепочка, либо в мешке П должна лежать такая же цепочка, как первая цепочка мешка С. Пустой цепочки у нас в распоряжении нет, значит верен второй вариант – кладем такую же цепочку (цепочку длины 2) в мешок П.

Теперь проверяем, что в мешке С лежат результаты склеивания всех цепочек, которые теперь лежат в мешках П и Р: добавляем в мешок С вторую из имеющихся цепочек длины 2.

Теперь изучаем цепочки мешка-результата – какие из них не могут получиться склеиванием тех, которые уже лежат в мешках П и Р. Находим такую цепочку – четвертую. Судя по ней, в мешке Р должна лежать цепочка из одной красной треугольной бусины – она у нас как раз осталась последней из тех, что есть в нашем распоряжении. Кладем цепочку и  проверяем, что при склеивании получившихся мешков цепочек действительно получается мешок-результат. Это так.

Задача 157. В этой задаче в результате склеивания в мешке-результате получаются и слова, не имеющие смысла в русском языке, но это нестрашно. По имеющемуся в мешке-результате слову ПОРА делаем вывод, что в пустом окне второго мешка-аргумента должно быть слово РА, а по цепочке КОРА в мешке-результате  находим недостающее слово в первом мешке-аргументе – КО. Осталось проверить, что полученное равенство верно.

Задача 158. Аналогичные задачи ребятам уже встречались. В таких случаях каждую из пропущенных команд дети могут найти перебором возможных команд, учитывая клетки, закрашенные Робиком.

Ответ:

Программа Х:

ВЛЕВО
ВНИЗ
ВПРАВО
ВПРАВО
ВНИЗ
ВВЕРХ
ВВЕРХ
ВПРАВО
ВВЕРХ
ВЛЕВО
ВВЕРХ
ВНИЗ

Задача 159. Усложненная задача на расстановку слов в алфавитном порядке. Здесь встречаются наиболее сложные случаи расстановки слов. В частности, случаи: когда слова имеют общие начала, одно слово является частью другого, в слове имеется дефис. Тем не менее, в настоящее время все эти случаи должны быть ребятами усвоены, поэтому данную задачу можно предлагать почти всем учащимся (за исключением самых слабых).

Задача 160. Знакомая ребятам задача, которую они решают либо перебором, либо анализом программы. В данном случае в ходе выполнения программы Робик сдвигается на 4 шага вниз, поэтому нет смысла запускать его из клеток четырёх нижних строк поля. Кроме того, в процессе выполнения программы Робик сдвигается на 4 клетки вправо, поэтому нет смысла запускать его из четырёх крайних правых столбцов. Теперь перебор оказывается не слишком велик – нам подходит первая клетка третьей строки.

Задача 161. Необязательная. Задача ориентирована в основном на средних учеников. На первый взгляд задача кажется довольно затейливой, но при анализе утверждений ситуация быстро проясняется. Действительно, если отбросить все знаки, которые имеют красные элементы, у нас остается ровно 8 разных знаков – из них мы и будем строить нашу цепочку, поскольку ее длина как раз восемь. При этом условие, что в цепочке 3 круглых знака, выполняется автоматически. Остается расставить знаки в цепочку так, чтобы за каждым круглым знаком следовал квадратный.

Компьютерный урок  «Склеивание мешков цепочек», 2 часть, задачи 162 – 169

Задача 162. Задача на склеивание мешков букв. В данном случае во втором мешке-аргументе имеется пустая цепочка. Смысл склеивания должен  быть уже понятен ребятам – получаются цепочки точно такие же, как в первом мешке-аргументе, а говоря проще – слова из первого мешка. Приклеивая к каждой цепочке букву Ю, мы сознательно добиваемся того, что в мешке результате получаются и другие понятные слова из русского языка, имеющие окончание Ю.

Задача 163. Задача продолжает линию задач на склеивание мешков цепочек, но имеет усложненный вид. Важно, чтобы ребята не запутались, ведь зеленых треугольных бусин появляется слишком много. Как и прежде мы предлагаем осуществить взаимный контроль – пусть ребята поменяются местами и попытаются найти ошибки друг у друга.

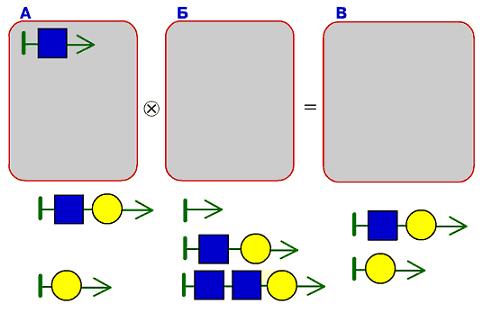
Задача 164. Задача на склеивание и разрезание цепочек бусин. Поскольку здесь в мешках-аргументах и мешке-результате не дано ни одной цепочки, детям необходимо провести некоторые рассуждения с опорой на полученный ими к этому моменту опыт.
Среди данных нам цепочек мы видим 5 цепочек с первой синей квадратной бусиной, среди них есть и цепочка из одной синей квадратной бусины. Это дает нам возможность предположить, что цепочка, состоящая из одной синей квадратной бусины, будет располагаться в мешке А.

Поскольку среди данных имеется всего одна пустая цепочка, то расположена она, несомненно, в мешке-аргументе, но в каком, пока не ясно.  Логично предположить, что наличие двух цепочек, состоящих из одной желтой круглой бусины, есть результат склеивания с пустой цепочкой, и если поставить  цепочку из одной жёлтой круглой бусины в мешок А, то в мешке-результате должны будут появиться цепочки, начинающиеся с круглой желтой бусины, но у нас остается всего одна такая цепочка. Значит, пустая цепочка несомненно содержится в мешке А, а цепочка из одной жёлтой круглой бусины – в мешке Б. Заполняем мешок-результат.

Теперь у нас остается всего 3 цепочки, две из них одинаковые. Пользуемся тем, что в мешке А есть пустая цепочка, кладем эти одинаковые цепочки в мешки Б и В.

Теперь видно, что в мешке-результате должна лежать цепочка из двух синих квадратных и желтой круглой бусин – именно она у нас и осталась. Проверяем результат – задача решена.

Задача 165. Задача на закрепление листа определений. Эта задача отличается от задачи 162 лишь объемом. Подсчитав количество склеиваемых цепочек в мешках-аргументах (2 и 6), делаем вывод, что в мешке результате будут заполнены все окна. Далее заполняем мешок-результат, используя по одной основе русских слов. Возможно часть ребят смутит повторение окончания Е, но ведь это не противоречит никаким условиям и в мешке результате получится по два слова ВОЛНЕ и два слова ПОБЕДЕ.

Задача 166. Задача аналогична компьютерной задаче 149. Как и в задаче 149, здесь полезно сначала выделить три участка рисунка Робика, соответствующие трём конструкциям повторения, – по сути, разбить задачу на подзадачи. После этого с каждой конструкцией повторения можно работать отдельно.

Задача 167. Конечно, эта задача давно уже стала для ребят знакомой и привычной, но это не значит, что всем будет решить ее очень легко. Как видите, китайские иероглифы довольно сложно различать и сравнивать между собой. Поэтому кому-то потребуется на эту задачу довольно много времени. Полный перебор оказывается здесь слишком большим, разделить фигурки на группы по некоторому признаку тоже не так-то просто, поскольку детям будет сложно выделить этот признак. Большинство ребят будут, рассчитывая на везенье, хаотично сравнивать различные пары фигурок между собой.

Задача 168. Эта задача знакома ребятам еще из курса 2 класса. В настоящий момент ее есть смысл предлагать в основном слабым (и некоторым средним) учащимся.

Задача 169. Данная задача более напоминает математическую, но определенный порядок наполнения кошельков все же есть. Например, удобнее сумму в 55 копеек набирать из двух монет – 50 и 5 копеек, хотя существует вариант, когда в кошельке окажется 5 - десятикопеечных монет, 1- пятикопеечная, 2 – десятирублевых, 1 – пятирублевая и 1 монета достоинством в  1 рубль. Словом ответов много и если на уроке осталось время, предложите ребятам собрать как можно больше вариантов решения.