Информатика. 3–4 класс (часть 2) Демо+методичка

Урок 17. «Выравнивание, решение необязательных и трудных задач»

Решение задач из учебника

Задача 90. Необязательная. Стратегии решения таких задач подробно описаны в комментарии к задаче 44.

Задача 91. Необязательная. Задача на повторение темы «Перед каждой бусиной. После каждой бусины». Особенность этой задачи состоит в том, что значки, которые в ней использованы, непривычны, и детям придется много раз обращаться к сноске, чтобы вспомнить, какой значок обозначает какой вид спорта.

Несложно заметить, что, во-первых, каждая фигурка в задаче представлена в трех экземплярах. Во-вторых, четыре фигурки различных видов можно сложить в один фрагмент цепочки так, что оба утверждения станут истинными. Дальше можно взять снова четыре разные фигурки и сложить их в том же порядке. После этого и последнюю четверку упорядочить так же. При этом утверждения подсказывают такой порядок следования значков в каждом из трех фрагментов: «велоспорт – фехтование – футбол – теннис» или «фехтование – велоспорт – теннис – футбол».

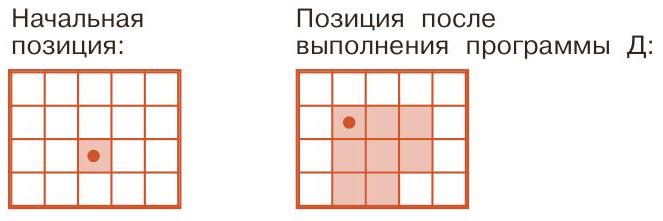
Задача 92. Необязательная. Имеется восемь (закрашенных) клеток, на каждой из которых Робик мог находиться перед выполнением программы. Здесь детям поможет метод перебора (полного или систематического). Чтобы осуществить полный перебор, необходимо поочередно выбирать каждую из закрашенных клеток в качестве начального положения Робика и пытаться из нее выполнить программу (можно использовать запасное поле с листа вырезания). Если при этом получается позиция, приведенная в задании, мы нашли начальное положение; если в какой-то момент Робик вышел за пределы закрашенных клеток, то предполагаемое начальное положение вычеркиваем и переходим к другой клетке. При этом, естественно, следует выполнять программу и вычеркивать клетки на разных полях, иначе легко запутаться.

Многие ученики догадаются, что из некоторых позиций запускать Робика просто нет смысла. Например, если поместить Робика в верхнюю закрашенную строку, он первым же ходом выскакивает в незакрашенную часть. Постепенно становится ясно, что Робик должен начинать выполнять программу из второй снизу строки. И действительно, анализ программы показывает, что в результате ее выполнения Робик сместился по вертикали сначала вверх на одну клетку, а затем на две клетки вниз (потом еще раз на две клетки вверх, но это уже не столь важно). Чтобы не выйти за пределы закрашенных клеток, ему надо стартовать в среднем ряду. Применяя то же рассуждение для перемещений по горизонтали, видим, что сначала Робик сдвинулся на одну клетку вправо, а затем – на две влево. Такое возможно только из средней клетки среднего ряда, она и дает положение Робика до выполнения программы. Осталось выполнить программу и отметить конечное положение Робика.

Есть и другой способ решения таких задач. Можно выполнить программу на клетчатой бумаге (на «поле без границ») и посмотреть, из какой клетки конечного рисунка Робик начал движение. Останется перенести результат на заданное поле для Робика. Этот способ, с одной стороны, облегчает работу, но с другой стороны, необходимое при этом способе перенесение результата может оказаться затруднительным. Поэтому мы бы предпочли, чтобы ребенок сам изобрел для себя такой способ: сделав интеллектуальное усилие, он наверняка будет способен довести решение до конца. Если же навязать такой способ решения, то продолжение работы может оказаться слишком сложным для ребенка.

Ответ:

Задача 93. Необязательная. Дети, скорее всего, будут решать эту задачу методом проб и ошибок, и не нужно им мешать. Если у кого-то дело совсем не идет, посоветуйте ему построить две какие-нибудь любые цепочки, для которых справедливо переместительное свойство. Так, если взять две цепочки длины 1, состоящие из разных бусин, переместительное свойство выполняться не будет, а если цепочки будут из одинаковых бусин – будет. Постепенно становится ясно, что переместительное свойство выполняется для пары одинаковых цепочек. Этот факт в данной задаче позволяет построить решение.

Задача 94. Необязательная. Задача на повторение лексики, связанной с деревьями, а также на работу с утверждениями, не имеющими смысла в какой-то ситуации. Здесь дети впервые сталкиваются с такими утверждениями для деревьев. На листах определений на с. 19 – 20 эта тема обсуждается, и приводятся утверждения, не имеющие смысла для данных деревьев. Напомните об этом тем детям, которые будут решать задачу.

Какие рассуждения могут помочь при решении задачи? Рассмотрим третье утверждение: «В этом дереве предыдущая буква перед Т – буква О». Для дерева L оно не имеет смысла, так как буква Т в нем не одна, а для деревьев R, S, Q оно не имеет смысла, так как буквы Т в них нет. В дереве N буква Т есть, причем одна. Кроме того, предыдущая бусина перед Т – буква О, поэтому для дерева N третье утверждение истинно. Аналогичные рассуждения подойдут и для четвертого утверждения.

Деревья устроены из знакомых учащимся слов, но значение некоторых слов они могут не знать. Если кто-то не знает значение слова, попросите найти это слово в толковом словаре.

Ответ:

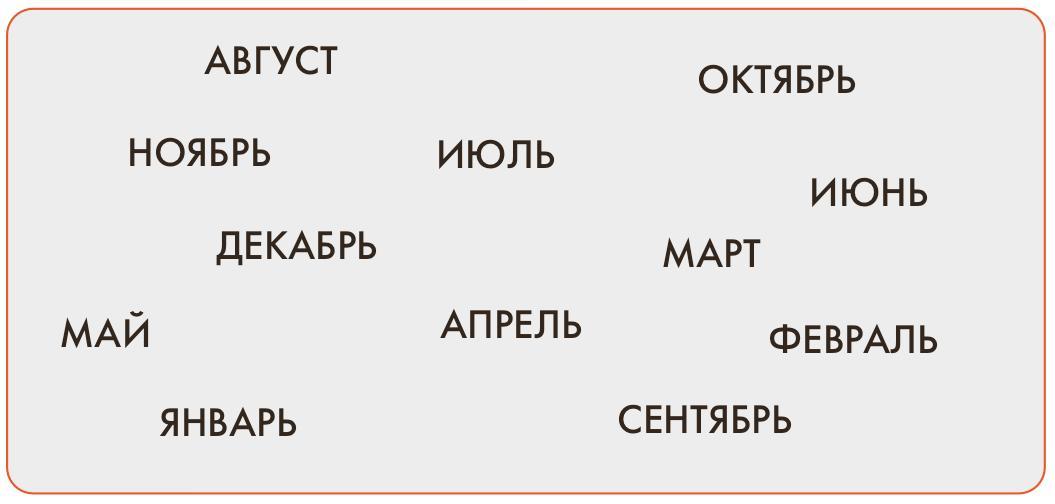
Задача 95. Необязательная. Задача довольно сложная. Однозначно по количеству букв определяются только слова МАЙ и СЕНТЯБРЬ, при заполнении других окон полной однозначности нет. Например, имеются три слова длины 4: ИЮНЬ, ИЮЛЬ и МАРТ. Если ученик не успел еще об этом подумать, то, увидев цепочку из четырех пустых окон, может написать туда, предположим, МАРТ – в этом случае довести до конца решение ему уже не удастся. Поэтому в данной задаче ребенок не сможет действовать чисто формально, ему каждый раз придется сопоставлять сразу несколько окон и слов. При этом возможны ошибки.

Ответ:

Задача 96. Необязательная. Задача напоминает задачу 93, но в отличие от нее здесь не удается построить решение из двух одинаковых цепочек. Детям снова поможет метод проб и ошибок. Постепенно в ходе этих проб становится ясно, что надо как-то использовать одинаковые бусины. Например, можно построить обе цепочки из бусин одинаковой формы и цвета. Тогда длина цепочек может быть любой, и можно обеспечить выполнение второго утверждения. Скорее всего, дети построят именно такое решение, но есть и другие варианты. Так, можно построить обе цепочки из одинаковых фрагментов любой длины. В цепочку А нужно взять столько фрагментов, чтобы выполнялось второе утверждение, а в цепочку Б – любое число. Вот пример цепочек А и Б, построенных из одинаковых фрагментов длины 3.

Задача 97. Необязательная. Подобные задачи дети уже решали (это задачи 32 и 43). В этой задаче мешков меньше, но различных предметов в мешках больше. Можно обсудить с детьми, которые решили все три задачи, какую задачу, по их мнению, проще решать и почему. Скорее всего, данная задача покажется ребятам сложнее, чем задачи 32 и 43.

Ответ: два одинаковых мешка – М и Н.

Задача 98. Необязательная. Больше других эта задача напоминает задачу 86, только здесь результат склеивания не задан явно, но известно, что должно получиться русское название животного. Как и в задаче 86, здесь предполагается перебор. Но он был бы очень большим, если бы детям по ходу дела не помогали лингвистические соображения. Так, для большинства цепочек в мешке сразу видно, может ли она быть началом или концом слова – названия животного. Это позволяет сократить перебор, а не сопоставлять каждое слово с каждым. Начало слова (первый аргумент), для которого не найдется окончание (второй аргумент), можно сразу вычеркивать. Так постепенно количество вариантов решения будет сужаться.

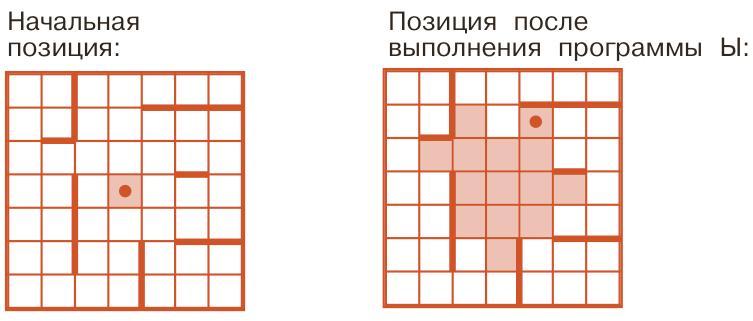
Задача 99. Необязательная. Положение Робика до выполнения программы не задано. Начальным положением для Робика может служить любая из закрашенных клеток, и в зависимости от выбора клетки возможные варианты программы Е могут быть самыми разными, в том числе и по длине. Естественно, чем больше Робик возвращается, т. е. чем больше клеток он посещает дважды, тем длиннее программа. При этом правильным ответом считается любая программа, в результате выполнения которой Робик закрашивает на поле данный рисунок. Ученики будут стремиться к простоте программы интуитивно, из соображений здравого смысла. Большинство ребят «запустят» Робика из конца верхней или нижней палочки буквы Е.

Задача 100. Необязательная. Эту задачу можно разделить на две части: сначала решить вопрос о цвете пропущенных бусин, а затем об их форме. Из первого утверждения следует, что пятая бусина синяя, из второго – что вторая бусина зеленая, из третьего – что шестая бусина красная. Не определился только цвет третьей бусины. Он может быть любым, в том числе и синим. Теперь начинаем разбираться с формой бусин. Самое простое решение одновременно и самое естественное – раскрасить окна в найденные цвета, т. е. сделать все бусины квадратными. Поскольку ни в одном утверждении про квадратные бусины не говорится, то на истинность утверждений квадратные бусины не повлияют. Таким образом, мы получили цепочку Г (на самом деле с учетом возможных цветов третьей бусины мы получили шесть разных вариантов цепочки Г). Возможно, кто-то захочет определить форму недостающих бусин «по-честному», т. е. провести полные рассуждения. В этом случае важно проследить выполнение условия, если какие-то бусины в окнах окажутся круглыми, треугольными или синими.

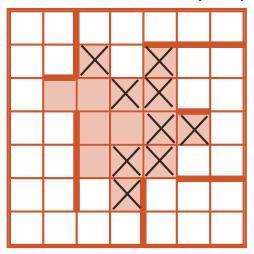
Задача 101. Необязательная. Подобную задачу дети уже решали (задача 92). Ребята, скорее всего, будут решать ее методом проб и ошибок и, возможно, найдут правильное начальное положение, но чтобы найти его наверняка, нужно воспользоваться методом перебора. Решение состоит в том, чтобы поочередно ставить Робика в закрашенные клетки и пытаться выполнить из них данную программу. Перебор можно существенно уменьшить, если внимательно посмотреть на команды программы. Сразу можно вычеркнуть клетки, из которых нельзя выполнить две первые команды вправо. Таких клеток оказывается довольно много. Остается проверить только пять оставшихся клеток:

Рисунок, который закрасил Робик в результате выполнения программы, довольно причудливый. Поэтому анализировать отдельно положение Робика на поле по горизонтали и по вертикали (как мы это делали в задаче 92) здесь сложно. Таким образом, попытки продолжения анализа программы с целью еще уменьшить перебор не дают большого эффекта. Здесь проще проверить все оставшиеся варианты.

Проверьте, что ребята не забыли отметить также и положение Робика после выполнения программы на соответствующем поле.

Ответ:

Задача 102. Необязательная. В первой части курса приводилось много примеров объектов и явлений, являющихся цепочками (последовательностями). Здесь детям предлагается поработать еще с одним таким примером. Обратите внимание, что направление цепочки противоположно направлению движения животных. Начало и конец цепочки задает условие: «Первым идет аист… Последним в цепочке идет жираф». В соответствии с этим нужно вписывать слова в утверждения. Для утверждений, где использованы понятия раньше/позже, есть несколько верных вариантов ответов.

Ответ:

Первым идёт аист.
Жираф идёт четвёртым после аиста.
Страус идёт позже аиста/жеребёнка.
Вторым с конца идёт слонёнок.
Жеребёнок идёт раньше страуса/слонёнка/жирафа.
Третьим идёт аист/жеребёнок/слонёнок/жираф.

Компьютерный урок «Выравнивание, решение необязательных и трудных задач», задачи 106 – 113

Задача 105. Задача на построение цепочки по описанию. Условий на цепочку накладывается совсем немного, поэтому подходящих решений имеется большое множество. В том числе можно собрать эту цепочку из частичных решений вида «оранжевая бусина – … – зеленая бусина».

Задача 106. Из условия нетрудно понять, что цепочка состоит из восьми круглых бусин разного цвета. После этого можно сразу поставить в цепочку оранжевую, красную и синюю бусины так, чтобы были истинны первое и третье утверждения. Затем оставшиеся бусины можно поставить в цепочку на любые места.

Задача 107. Задача на построение дерева по описанию. Сразу стоит разместить на каждом уровне по 2 листа. Теперь подумаем, сколько у нашего дерева может быть корневых бусин. Их должно быть больше пяти, но стоит заметить, что корневых бусин в дерева не может быть больше, чем листьев (подумайте, почему!). Значит в нашем дереве 6 корневых бусин – 2 листа и 4 не листа. При этом заметим, что на втором уровне не может быть больше 4 бусин, значит каждая корневая бусина, которая не является листом, имеет ровно одну следующую бусину. Таким образом, по структуре все решения ребят будут схожими, деревья будут отличаться только формой и цветом бусин, из которых они  состоят.

Задача 108.Задача аналогичная компьютерной задаче 102. Отличие данной задачи состоит в том, что на поле здесь есть внутренние стенки, поэтому и возможных программ не так много. Например, из начальной позиции Робик может выполнить только одну команду – «вверх».

Задача 109. Задача на повторение темы «Склеивание цепочек». Больше подойдет для средних и слабых учеников.

Задача 110. Задача на построение цепочки чисел. Из данной таблицы можно сделать вывод, что наша цепочка состоит из двузначных чисел, больших 95. Таких чисел всего четыре: 96, 97, 98, 99, а длина нашей цепочки – восемь. Поэтому числа в цепочке будут повторяться в любом случае, и третье утверждение будет ложно автоматически. Что касается расположения чисел в цепочке, об этом ничего в утверждениях не сказано, поэтому решений в данной задаче довольно много.

Задача 111. На  первый взгляд эта задача может показаться довольно затейливой, ведь придется сопоставлять 4 утверждения. Однако ситуация довольно быстро проясняется, если использовать утверждения в правильном порядке. Все фигурки у нас разные, причем все корневые вершины – бабочки. Бабочка в нашей библиотеке лишь одна, значит в дереве одна корневая вершина – бабочка. Все следующие вершины после бабочки – рыбы, но все рыбы у нас листья. Значит, все вершины второго уровня – это рыбы–листья. Таким образом выясняется, что наше дерево имеет 2 уровня вершин: на первом – одна корневая бабочка, на втором – рыбы-листья. Единственное, что не регламентировано условием – число рыб на втором уровне. Этим и будут отличаться решения детей – наименьшее число рыб две, наибольшее – семь (ведь все рыбы у нас должны быть разными).

Задача 112. Аналогичные задачи ребятам уже встречались. Решение здесь однозначное, недостающие в программе команды следующие: вверх, вверх, влево, влево.

Задача 113. Как видите, это довольно необычная задача. С одной стороны, это задача на повторение темы «Таблица для мешка». С другой стороны, это пограничная задача с курсом русского языка. В частности, она позволяет детям сделать несколько интересных языковых наблюдений. Так оказывается, что число гласных в слове не напрямую связано с числом букв. Тем не менее, многим детям может казаться, что чем больше в слове букв, тем больше там и гласных, но это не так. Например, в данной задаче дети могут найти примеры слов, в которых на 6 букв приходится лишь одна гласная или же наоборот – на три буквы приходятся две гласные.