Информатика. 3–4 класс (часть 2) Демо+методичка

Уроки 11-12. «Перед каждой бусиной. После каждой бусины»

Мы живем в мире постоянно повторяющихся событий и явлений. Периодические цепочки играют в нашей жизни достаточно важную роль: смена времен года, месяцев, дней недели, дня и ночи, часы, идущие по кругу, – примеры периодических цепочек, в основе которых лежит конструкция «после каждой»: после каждого дня идет ночь, после каждого вторника – среда, после каждого января – февраль и т. д. С периодическими цепочками мы пока работать не будем, а познакомим детей с понятиями после каждой и перед каждой. Как и раньше, на этом листе определений мы рассматриваем ситуации, в которых утверждения становятся бессмысленными.

Решение задач из учебника

Задача 65. Несмотря на то что это первая задача после листа определений, кто-то из ребят может сделать ошибку, поскольку цепочка Ц длинная, и красных треугольных бусин в ней довольно много. Поэтому обратите внимание на проверку в этой задаче. На первом этапе такой проверки можно предложить детям сравнить число красных треугольных бусин в цепочке Ц и число бусин обведенных зеленым. Тем ребятам, у кого эти числа совпали, можно предложить поменяться тетрадями и осуществить более подробную проверку в парах.

Задача 66. Дети наверняка легко справятся с этим заданием и получат в цепочке слово СКАКАЛКА. Обратите внимание на второе утверждение. Хотя дети, скорее всего, интуитивно поймут его правильно и без дополнительных рассуждений, это утверждение содержит «подводные камни». С точки зрения формальной логики (и предыдущих листов определений) утверждение «В этом слове буква С идет раньше буквы Л» означает, что в данном слове есть только одна буква С, есть только одна буква Л и при этом С идет раньше Л. Это хороший пример, который объясняет, зачем мы постоянно обсуждаем ситуации, в которых утверждения становятся бессмысленными. Если кто-то из учеников задавал вам подобный вопрос («Зачем все это?»), обсудите с ним индивидуально, что без этого было бы трудно коротко сформулировать такое задание, как в задаче 66.

Задача 67. Эта задача далеко не такая простая, как может показаться сначала. Во-первых, в самом утверждении: «...третья фигурка перед каждой морковкой – луковица» заложен принцип построения цепочки «от конца к началу», что для детей пока сложно. Во-вторых, чтобы это утверждение стало истинным, придется учесть целый ряд условий. Наш совет – поработать сначала с вырезанными фигурками с листа вырезания – будет здесь актуален не только для слабых детей, но практически для всего класса. Скорее всего, ребята будут решать методом проб и ошибок: складывать различные цепочки, проверять для них истинность утверждения и в случае неудачи возвращаться на шаг (или на несколько) назад. Большинству ребят проб потребуется достаточно много. Чтобы не тратить время на стирание и не разводить грязь в тетради, советуем производить все пробы на вырезанных фигурках. Возможность легко поменять фигурки местами, разобрать цепочку и собрать заново позволит ребятам в ходе проб и ошибок быстрее понять, «как все устроено»: как не надо строить цепочку и к чему необходимо стремиться.

После нескольких проб действия ученика становятся более осмысленными, и вот уже искомая цепочка выложена на столе. Теперь необходимо соединить в таком же порядке фигурки в тетради. Хорошо, если ребенок будет стремиться к тому, чтобы цепочка не пересекала себя и выглядела красиво. Возможно, кто-то догадается, что здесь цвет овоща не играет никакой роли, поэтому, например, две луковицы разного цвета можно легко поменять местами.

Задача 68. В данном случае сразу можно использовать только второе утверждение. Поэтому наиболее очевидное решение – нарисовать две квадратные бусины, а затем начать их «обстраивать». Слабым ученикам можно выдать полный набор бусин (он есть на листе вырезания), пусть попробуют сначала сложить такую цепочку на столе.

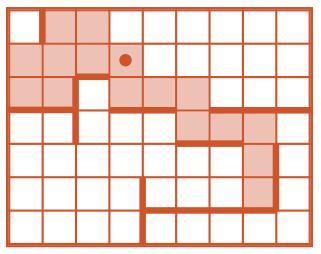
Задача 69. Необязательная. В процессе выполнения программы Робик как будто «обходит» стены, расставленные на поле (или ищет выход из лабиринта). Это в некотором смысле упрощает детям задачу, ведь при неправильном выполнении команды Робик во многих случаях просто упрется в стену, и придется решать задачу заново. Именно для таких случаев и приводятся дополнительные поля на листе вырезания.

Ответ:

Задача 70. Упражнение на проверку того, насколько качественно дети усвоили тему нового листа определений.

Задача 71. Это первая задача нового типа. Здесь впервые необходимо полностью написать программу для Робика, имея его начальную позицию и позицию после выполнения программы. Путь Робика достаточно прост, ему незачем возвращаться, проходить дважды по одним и тем же клеткам. Скорее всего, программа получится следующая:

Хотя это и не единственный вариант программы. В любом месте Робик может сделать шаг назад и потом опять пойти дальше по указанному пути. Такая программа не будет оптимальной, но мы вопрос оптимальности программ с детьми не обсуждаем.

На примере этой задачи ребята должны выработать определенный способ действий, который поможет при решении подобных задач в дальнейшем. Самый простой способ действий – пошаговое написание и параллельное выполнение программы. Можно использовать при этом запасное поле с листа вырезания. Начинаем с того, что переносим на новое поле начальное положение Робика. Затем, глядя на позицию Робика после выполнения программы, прогнозируем, куда должен двигаться Робик из начального положения. Записываем первую команду, выполняем ее и т. д. При таком способе действий выполнение программы играет роль обратной связи, которая, с одной стороны, дает возможность не отклоняться от данной траектории Робика, а с другой – не забыть, какая команда следующая.

Задача 72. Здесь детям предстоит сопоставить инструкцию с ее предполагаемыми результатами и среди них выбрать нужный. Какие стратегии решения здесь можно выбрать? Первая – поочередно брать каждую из цепочек и проверять для нее пункты инструкции. При этом, как только сталкиваемся с тем, что какой-то пункт инструкции не выполняется, останавливаемся и выбрасываем цепочку из дальнейшего рассмотрения (например, ставим около нее прочерк). Затем берем следующую цепочку и т. д. Такая стратегия подходит и для слабого ребенка (возможность запутаться здесь минимальна), однако времени на эту работу уйдет довольно много. Вторая стратегия – поочередно брать пункты инструкции и проверять их выполнимость для каждой цепочки. Если какой-то пункт для какой-то цепочки не выполняется, то ее сразу вычеркиваем и остальные пункты инструкции для нее уже не проверяем. За счет этого происходит экономия времени.

Ответ: Надя раскрасила цепочку Ц.

Задача 73. Некоторую трудность может вызвать применение понятия все для одного предмета. Такая ситуация уже встречалась в задаче 36. Из других утверждений ошибку по невнимательности может вызвать четвертое утверждение – ребята могут не заметить синий треугольный лист, который «прячется» на пятом уровне.

Ответ: первое, третье, шестое и седьмое утверждения истинны; остальные утверждения ложны.

Задача 74. Все учащиеся к моменту выполнения задачи должны понимать, что значит «Робик сможет выполнить программу»: они должны помнить, что Робик ломается, если программа заставляет его пройти через стену или через границу поля. Задача детей написать такую программу, чтобы Робик не «натыкался» на стены. При этом Робик может несколько раз проходить по одним и тем же клеткам, что облегчает задачу.

Проверку можно провести в парах: например, после того как оба ученика выполнили задание, попросить их поменяться тетрадями и выполнить программу соседа на таком же поле с листа вырезания. Другой способ парной проверки – попросить ребят только написать программу Т, а затем поменяться тетрадями. В этом случае каждый ученик выполняет не свою программу, а программу соседа. Если Робик ее смог выполнить, то в тетради появляется законченное задание, а если обнаруживается ошибка, то тетрадь возвращается автору и он переделывает программу.

Задача 75. Необязательная.

Ответ:

Задача 76. Необязательная. При внимательном прочтении второго утверждения становится понятно, что все листья дерева Т должны быть расположены на третьем уровне.

Задача 77. Необязательная. Главное в задаче – работа с утверждениями, которые не имеют смысла.

Напомним, что при определении истинности утверждений типа «В этом слове предыдущая буква перед А – буква З» мы предполагаем, что в слове имеется ровно одна буква А, а также в цепочке имеется предыдущая буква перед А. Только в этом случае можно достоверно сказать, что предыдущая перед буквой А буква З (тогда утверждение истинно) или не буква З (тогда утверждение ложно). В случае, если буквы А в слове нет, если букв А несколько (тогда непонятно, о какой из них идет речь) или буква А – первая в цепочке (нет буквы, предыдущей перед А), утверждение для данного слова не имеет смысла. Эта ситуация принципиально отличается от той, когда мы пишем «Н», говоря, что значение утверждения неизвестно. В таком случае мы не отрицаем возможности анализа утверждения с точки зрения его истинности или ложности, просто говорим, что информации, необходимой для этого анализа, у нас пока нет. Если же мы сталкиваемся с ситуацией, когда бусина не одна или ее нет, то мы вообще выбрасываем из рассмотрения такие утверждения как некорректные и поэтому не поддающиеся анализу.

Скорее всего, самое большое число ошибок вызовет третье утверждение для слова U. Ошибки эти связаны с тем, что ребята могут пытаться как-то домыслить и переформулировать (конечно, интуитивно) утверждения, которые сформулированы некорректно. Поэтому, видя, что одна буква Е в этом слове идет позже буквы В и другая буква Е идет позже буквы В, кто-то может сделать вывод об истинности утверждения. Однако мы с вами помним, что основная задача курса – привить ребятам навык мыслить в рамках формальной логики, научить их работать в рамках общих правил.

Ответ:

Компьютерный урок «Перед каждой бусиной. После каждой бусины», 1 часть, задачи 73 – 80

Задача 73. В этой задаче ребята закрепляют понятия «перед каждой» и «после каждой», в ходе работы используя компьютерный инструмент «галочка». Если кто-то из детей ошибется в одном из заданий, посоветуйте ему выделить в цепочке сначала каждое яблоко (или грушу), а потом уже пометить фигурку после каждого яблока (или перед каждой грушей).

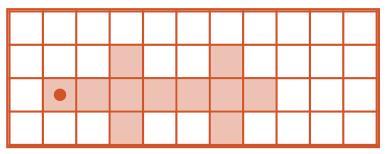
Задача 74. Для некоторых детей здесь сложность будет представлять длина цепочки А. Как видите, цепочка у нас длинная, на странице она изгибается, поэтому часть ее идет слева направо (как обычно), а другая часть справа налево. Это может вызвать ошибки в определении следующей бусины и второй бусины перед.

Задача 75. В этой задаче ребята строят цепочку по описанию, включающему новые понятия «перед каждой» и «после каждой». Из первого и третьего утверждения следует, что в цепочке есть ровно два фрагмента «кошка – курица». Если добавить к этому еще и второе утверждение, то получаются два фрагмента «мышка – кошка – курица». Поскольку цепочка имеет длину 7, остается добавить в нее еще одну фигурку. Чтобы утверждения остались истинными, это должна быть не курица и не кошка.

Задача 76. В этой задаче ребята могут понять на собственном опыте разницу между двумя утверждениями, которые на первый взгляд означают одной и то же: «Следующая буква после каждой К – буква А» и «Предыдущая буква перед каждой А – буква К». На самом деле эти утверждения имеют разное содержание. Они могут иметь для некоторых слов не только разные значения истинности, но одно из них может оказаться бессмысленным, в то время как другое имеет смысл. Так для слова КОШКА первое утверждение ложно, а второе – истинно. А для слова КАК первое утверждение бессмысленно, а второе – истинно. Надеемся, никого из ребят не смутит ситуация, когда в слове ровно одна буква А или одна буква К. Для таких случаев мы употребляем понятия «перед каждой/после каждой» как обычно.

В результате нам подходит всего 8 слов: КАПЕЛЬКА, МОРОШКА, КАРТОШКА, КАКАО, КАКАДУ, КАШКА, МОШКА, КАЛИТКА.

Задача 77. Здесь необходимо вставить слова в цепочку так, чтобы не нарушился словарный порядок слов. Конечно, вариантов для каждого пропущенного слова много. Единственная сложность данной задачи заключается лишь в том, что первые буквы всех слов находятся в той части алфавита, в которой дети чаще всего путаются (с буквы У до буквы Щ), да и слова на такие буквы детям тоже встречаются существенно реже, чем на «популярные» буквы алфавита.

Задача 78. Аналогичные обратные задачи на поиск начального положения Робика по выполненной им программе ребятам уже встречались в бумажном учебнике. Решать такие задачи на компьютере существенно проще, чем на бумаге – можно просто «запустить» Робика из каждой клетки поля и посмотреть, что получится. Это не займет много времени и не отнимет много сил. Как только ребёнку встретится клетка, из которой Робику удалось выполнить данную программу, перебор можно остановить и отметить найденную клетку крестиком.

Задача 79. Задача на повторение листов определений «Длина цепочки», «Цепочка цепочек». Аналогичные задачи дети решали уже не раз, поэтому с этой задачей все ребята должны справиться самостоятельно.

Задача 80. Необязательная. Несмотря на то что эта задача на построение дерева по описанию, нетрудно понять, что она в значительной степени математическая. Действительно, наиболее сложным шагом в этой задаче является определение того, сколько монет каждого достоинства должно быть в дереве. Само построение дерева после этого не будет представлять никаких проблем. Определить число монет каждого достоинства можно при помощи полного перебора. Ясно, что в любом дереве должна быть хотя бы одна корневая вершина и хотя бы два листа. Поэтому перебор можно вести по пятирублевым или по двухрублевым монетам. Мы выбираем пятирублевые монеты, поскольку перебор в этом случае будет меньше. Итак, пусть в дереве 2 пятирублевых монеты. Видим, что сумму в 43 рубля 10 монетами никак не наберешь. Даже если использовать монеты наибольшего достоинства (по 2 рубля), то их понадобиться не меньше 16. Значит, надо брать пятирублевых монет больше. Можно добавлять монеты по одной, а можно сразу по несколько и смотреть, что получится. В результате получаем, что в нашем дереве 8 пятирублевых монет, 1 двухрублевая и 1 рублевая. Подходящих деревьев в этой задаче оказывается довольно много. У всех таких деревьев одна корневая вершина (монета в 2 рубля) и пятирублевые листья (которых может быть от двух до восьми). Монета в 1 рубль не будет листом. Теоретически число уровней в этой задаче может быть от трех до девяти. Однако, у детей не получится в этой задаче (как и в большинстве компьютерных задач) сделать больше четырех уровней.

Компьютерный урок «Перед каждой бусиной. После каждой бусины», 2 часть, задачи 81 – 88

Задача 81. На прошлом компьютерном уроке ситуации бессмысленных утверждений возникали, но неявно. Здесь же необходимо выделить все цепочки, для которых данное утверждение не имеет смысла. Такая цепочка оказывается всего одна – третья, поскольку у последней треугольной бусины в цепочке нет второй после нее. Цепочка, для которой утверждение истинно, в этой задаче тоже оказывается одна. Такая ситуация еще раз напоминает ребятам о том, что с точки зрения формальной логики понятие «все» можно употреблять и для случая, когда объект всего один.

Задача 82. Из условия задачи следует, что в цепочке будут все фигурки из библиотеки, ведь в библиотеке их всего 7, а все фигурки в цепочке должны быть разными. Что касается желтых фигурок, то их можно ставить не раньше четвертой, иначе второе утверждение в задаче потеряет смысл. Как видите, решений в этой задаче довольно много.

Задача 83. Третье утверждение на первый взгляд кажется очень сложным, но остальные утверждения помогают быстро разобраться в ситуации. Действительно, используем сначала информацию более простых утверждений – раскрасим все корневые бусины оранжевым, а все листья – синим. После этого у нас остались нераскрашенными только бусины второго уровня, которые не являются листьями, они являются предыдущими перед листьями. Значит (исходя из третьего утверждения) все такие бусины нужно раскрасить в зеленый цвет.

Задача 84. Эта задача аналогична компьютерной задаче 68. Подходящих программ очень много, и вряд ли кто-то из ребят ошибётся в этой задаче. Проследите, что все выполнили проверку, заставив Робика выполнить свою программу.

Задача 85. Здесь у всех слов первые буквы одинаковые, и вторые буквы тоже одинаковые. Кроме того, все слова делятся на две группы – с третьей буквой Б и третьей буквой В. Чтобы упорядочить слова в каждой группе, приходится сравнивать четвертые буквы. Также среди данных слов имеются два слова, одно из которых является частью другого (ЛАВА и ЛАВАШ). Возможно, с кем-то из ребят придется вспомнить, что в этом случае раньше идет слово меньшей длины.

Задача 86. Это довольно сложная задача, поэтому мы предлагаем такую задачу в компьютерном варианте, ведь так проще экспериментировать, меняя бусины местами.  В ней «работает» одна идея, которая пригодится ребятам в дальнейшем при решении подобных задач. Сложность этой идеи для ребят в том, что они уже привыкли строить цепочки из частичных решений, то есть, если в условии написано «следующая после каждой квадратной бусины – синяя», ребята строят пары «квадратная – синяя», а затем составляют эти пары в одну цепочку. Здесь такой метод не подойдет. Действительно, у нас две квадратные бусины и две синие бусины, но одна бусина одновременно является и синей и квадратной. То есть бусин только три, из них не получится составить две отдельные пары. Поэтому мы вынуждены сразу расставлять бусины так, чтобы принимать во внимание это обстоятельство.  Таким образом, у нас выстраивается кусочек «квадратная желтая – квадратная синяя – треугольная синяя». В точности так же дело обстоит и со вторым условием. Желтых бусин у нас 5, а треугольных – 6, но две бусины оказываются желтыми треугольными. Облегчает решение лишь то обстоятельство, что подходящих решений здесь довольно много. Вот одно из таких решений:

Задача 87. Эта задача выглядит для ребенка непривычно и кого-то может поставить в тупик. Но все встает на свои места, как только мы начинаем анализировать данные утверждения, сопоставляя их друг с другом и рассуждать. Лучше всего начать с двух последних утверждений. В мешке больше 7 красных фигурок, значит их самое меньшее 8. В мешке больше 6 зеленых фигурок, значит их самое меньшее 7. У нас получается уже 15 фигурок. Это означает, что в мешке ровно 8 красных и 7 зеленых фигурок, желтых фигурок в мешке просто нет. Имея это в виду, мешок оказывается построить не сложно. Подходящих решений здесь довольно много. Нам даже подойдет мешок, в котором лежат вообще одни груши – 8 красных и 7 зеленых (ведь ноль меньше четырех и меньше пяти), хотя дети вряд ли будут строить такой мешок.

Задача 88. Необязательная. Сложности в таких задачах возникают обычно у тех детей, которые пытаются раскрашивать одновременно с разных концов картинки. Лучше всего начинать раскрашивать с одной области, которая граничит с тремя областями, и двигаться от нее ко всем другим областям. Например, мы раскрасили красным один из четырех треугольников в центре. Тогда три соседние области нужно раскрасить в три разных цвета: желтый, синий, зеленый. Дальше ученик раскрашивает соседние с уже раскрашенными области, на каждом шаге проверяя, не появились ли две соседние области, раскрашенные в один цвет. Если не появились – продолжает раскрашивать дальше. Если – появились, возвращается на шаг назад.