Информатика. 3–4 класс (часть 1) Демо+методичка

Урок 13. «Сколько всего областей»

Топология

Математику часто определяли как науку о числах и фигурах. В современной математике роль чисел существенно меньше, как и роль фигур в их классическом понимании. Эти изменения находят отражение в нашем курсе: в нем, в частности, появляются начала топологии - важной и интересной области современной математики. Особое значение топология приобретает в связи с развитием информатики, начиная с проблем топологии интегральных схем и кончая задачами распознавания изображений компьютером.
Чтобы пояснить, чем занимается топология, можно сказать, что она изучает свойства фигур в пространстве, которые сохраняются при непрерывных преобразованиях этого пространства. Но это лишь приблизительное описание, в частности, потому, что математическое понимание пространства тоже не совпадает с нашим обычным пониманием и требует особого пояснения. Покажем это на следующем примере.

Давайте выберем в качестве пространства воздушный шар, только абстрактный, математический: его можно как угодно растягивать, сжимать, деформировать без всякого сохранения размеров, но не прорывать. Нарисуем на шаре какую-нибудь кривую, опять-таки «абстрактным», математическим пером: у этой кривой нет никакой толщины. Может случиться, что она разобьет шар на две области так, что в каждой из этих областей можно будет перейти от одной произвольной точки к любой другой, не пересекая нашу кривую. Вот пример такой кривой на шаре:

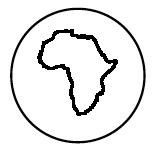
А вот примеры кривых на шаре, для которых рассматриваемое нами свойство не выполнено:

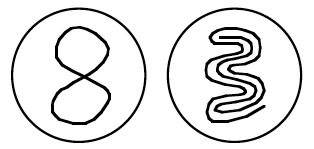
Итак, мы описали свойство кривой на шаре (точнее, на сфере, потому что для математиков шар - это заполненная сфера).
Вполне похоже, что обсуждаемое нами свойство является топологическим. Это значит, что если кривая разбивала сферу на две области и мы сферу как-то деформировали, то деформированная кривая будет опять разбивать деформированную сферу на две области.

И действительно, если соответствующим (и естественным) образом определить все используемые математические понятия, то получится математическое определение топологического свойства, отвечающее нашим интуитивным представлениям.
Многие понятия топологии, обладая формальными математическими определениями, имеют весьма ясное интуитивное содержание. Более того, это содержание иногда относится к базовым понятиям, описывающим окружающий нас мир. Поэтому некоторые из этих понятий довольно часто появляются в курсах разных авторов - в учебниках и рабочих тетрадях для 1 класса. Для нас задачи, включающие такой материал, являются частью начал образования, и заложенные в них идеи получают развитие на протяжении всего курса.

Кстати, приведем пример свойства, не являющегося топологическим: «Кривая ограничивает область, имеющую площадь 4 кв. см».

Число областей

Топология занимается фигурами и их свойствами, а не числами. Однако числа часто участвуют в определении тех или иных топологических свойств. Свойство, которое мы сейчас рассматриваем, тоже связано с числами. Это свойство - число областей в картинке. С самого начала при подсчете числа областей мы вводим цвет. На первый взгляд вам может показаться, что для подсчета числа областей вовсе не обязательно раскрашивать картинку. Но не спешите - так обстоит дело только в простейших случаях.
Как вы видите, при подсчете числа областей мы используем числовую линейку. Клетки линейки при этом раскрашены - мы так же раскрашиваем области картинки. При раскрашивании областей картинки (и клеток числовой линейки) мы используем все наши «рабочие» цвета, кроме черного. Черный цвет мы не используем из практических соображений - чтобы на клетках числовой линейки были виды все числа (черные), а на картинке - все черные внутренние линии.

Итак, на листе определений описывается довольно несложное чередование действий: пометка клетки числовой линейки - раскраска очередной области соответствующим цветом и т. д. Однако словесное описание этого несложного процесса ребенку порой понять нелегко. И дело не в том, что авторы не могут понятно описать простую вещь или специально хотят запутать непосвященных, - проблема здесь в объективной ситуации: точные словесные описания весьма простых действий иногда оказываются сложными, и проще объяснить их на конкретном примере, как мы часто и делаем в нашем курсе. Однако иногда другого способа, отличного от письменной коммуникации, нет. Поэтому наши дети должны уметь писать и понимать написанное. Описания имеют такие преимущества, как однозначность толкования и неизменность во времени (а что-то показанное или рассказанное можно забыть, или воспроизвести неточно).

Создание описания (программы) деятельности для компьютера называется программированием.

Решение задач из учебника

Итак, мы, как и раньше, начинаем решать задачи на данное определение. Мы постоянно сталкиваемся в классе с разным уровнем подготовленности учащихся к решению той или иной задачи. Естественная и продуктивная идея - работать с каждым учащимся в его «зоне ближайшего развития». Это означает, что, если у учащихся есть шанс самостоятельно разобраться в определении и решить задачу, нужно использовать эту возможность. Если необходимо помочь ребенку решить задачу, делайте это, по возможности не подталкивая его, а ожидая действий от него самого. Помните, в частности, что наша цель не только в том, чтобы учащийся решил конкретную задачу, но и в том, чтобы он научился разбираться в письменных определениях.

Обратите внимание, что цвета на числовой линейке повторяются. Это не должно вызывать недоразумений, если раскрашивание областей идет последовательно и аккуратно. По существу, при подсчете областей можно было бы обойтись даже одним цветом. Наличие нескольких цветов просто уменьшает возможные ошибки и позволяет допущенную ошибку исправить. Кроме того, раскрашивание разными цветами позволяет учащимся достигать эстетических эффектов.

Задача 63. Напомним еще раз, что картинка в данном случае - это все, что находится внутри рамки (если рамка есть). Обратите внимание на правую картинку. Чтобы не ставить в сложное положение детей с плохим зрением, глаза и нос кота мы предлагаем не считать. Интересно, что, хотя в изображении самого кота всего 2 области (голова и тело), в картинке в целом 5 областей. Найдите самостоятельно все 5 областей при подготовке к уроку.

Задача 64. Необязательная. Как видно из условия, в задаче использовано армянское слово. Конечно, то, как именно читается это слово по-армянски, совершенно необязательная информация для решения этой задачи. Но все-таки нам кажется, что такая задача может подтолкнуть любознательных детей к дальнейшим «лингвистическим исследованиям». Оказывается, непонятные буквы, с которыми они работают время от времени в учебнике, имеют собственные на звания, и с их помощью можно записывать слова! По возможности поддержите интерес таких детей.

Задача 65. Здесь (как и в правой картинке в задаче 63) снова создают некоторую сложность области фона. Детям довольно сложно привыкнуть, что единый элемент рисунка (фон) может состоять из нескольких областей. В данной картинке имеется 2 области фигурки (осьминога) и 3 области фона. Всего в картинке 5 областей.

Задача 66. Необязательная. Трудная задача. В ней мы сталкиваемся с конкретной ситуацией программирования, которую уже описывали. Выражение «Сделай... так, чтобы... » содержит описание класса действий (раскрась один квадратик) и класса ситуаций (среди фигурок есть две одинаковые). Понимание условия задачи начинается с представления о результате - одинаковость двух фигурок (из которых одна измененная). Затем следует случайный (или систематический) перебор пар, при котором возникает ощущение «близких» и «далеких» фигурок. Можно, используя это ощущение, продолжить поиски среди пар фигурок, кажущихся близкими. С точки зрения информатики речь здесь идет о создании программы по заданию (спецификации) результата ее работы (Сделай... так, чтобы...). Перебор можно существенно уменьшить, если заметить, что во всех фигурках, кроме одной, ровно один нераскрашенный квадратик. Если учесть требование условия (мы можем раскрасить лишь один квадратик в одной фигурке), то становится ясно: нужно из какой-то фигурки сделать такую же, как полностью раскрашенная (третья слева).

Задача 67. Несложная задача на текущий лист определений, которую можно использовать для промежуточного контроля или предложить ребятам на дом.

Трудные задачи

В учебнике имеется несколько задач, существенно более трудных, чем остальные. Они всегда необязательные. Какая же от них польза?
В классе наверняка найдутся дети, которые быстро решат все остальные задачи. Можно занять их решением трудной задачи. Некоторые дети могут обладать какими-то специфическими способностями и не так уж быстро решать задачи курса. Но как раз трудная задача у них получится. Это может послужить как основой для самоутверждения такого ученика, так и способом открытия в нем неординарных способностей.

Работая с якутскими учителями, мы обнаружили, что почти все они решают задачи графического характера значительно быстрее московских учителей, хотя в решении других задач находятся на обычном «московском» уровне. Потом оказалось, что аналогичные наблюдения уже были сделаны психологами до нас.

Неудавшаяся попытка решить трудную задачу может быть полезна для того, чтобы продемонстрировать ученику (и нам с вами), что, даже оперируя очень простыми базовыми понятиями, можно столкнуться с весьма сложными вопросами. Достаточно интересно каждый раз подумать, с чем же связана сложность.

Попробуйте заранее обдумать упрощенные варианты каждой из трудных задач; их вы сможете предложить тем ученикам, которые заинтересовались конкретной задачей, но не смогли ее решить самостоятельно. Желательно, чтобы ваша помощь не носила характера прямой подсказки - что именно нужно делать, а ограничивала задачу, давала только некоторые подходы к ее решению и т. д.

Мы бы очень хотели, чтобы задачи, которые мы даем детям в школе, в большей степени отражали те или иные стороны реальности, готовили их к встрече с ними в жизни. Понимание того, что бывают задачи, которые не сумеешь решить ты сам, может быть, и никто в классе, даже учитель и вообще никто, является важным жизненным знанием.

Компьютерный урок «Считаем области»

Решение задач

Задача 103. Это первая задача на подсчет областей картинки. Конечно, такие задачи в компьютерном виде решать гораздо проще, чем на бумаге. Действительно, «заливка» полностью берет на себя всю нагрузку по выделению областей, за один щелчок всегда раскрашивая целиком ровно одно область. Таким образом, от ребенка в этой задаче требуется только следование алгоритму, описанному на листе определений.

1 шаг. Раскрашиваем первую по счету нераскрашенную клетку числовой линейки любым цветом.

2 шаг. Раскрашиваем любую нераскрашенную область картинки тем же цветом.

3 шаг. Выбираем другой цвет.

4 шаг. Выполняем шаги 1 – 3.

Так действуем до тех пор, пока вся картинка не окажется раскрашенной.

Как видите, картинка для выделения областей довольно сложная, без поддержки «заливки» детям обойтись было бы затруднительно. Интересно, что, несмотря на большое число черных линий (границ областей), в этой картинке всего 4 области.

Задача 104. Это первая задача, в которой картинка нарисована в рамочке. В теме «Области» ребята уже работали с такими картинками. В частности, они должны были усвоить, что в картинку входят все области, находящиеся внутри прямоугольной рамочки (или круглой границы). Тем не менее, кто-то из учеников, возможно, это забыл. Если вы столкнетесь с ошибками такого типа, когда ребенок вообще не раскрашивает и не считает области фона, попросите ребенка вернуться к листу определений. Картинка с листа определений как раз в прямоугольной рамочке. Надо обратить внимание, что после подсчета областей на картинке не должно остаться ни одной нераскрашенной (белой) области.

В этой картинке 7 областей – 5 областей фона и 2 области фигурки кота. Сильным детям можно предложить решить данную задачу на бумаге, распечатав экран с задачей на принтере, а компьютерный вариант использовать в качестве проверки.

Задача 105. В этой задаче ребята повторяют сравнение наложением. Конечно, дети не будут сравнивать наложением каждую фигурку с каждой, ведь некоторые кружки отличаются по размеру настолько сильно, что это хорошо видно на глаз. Скорей всего, дети будут сравнивать наложением только близкие по размеру фигурки. Именно среди таких фигурок учащиеся постепенно найдут две одинаковые кружки.

Задача 106. Аналогичные задачи уже встречались ребятам. Решать ее наобум (методом проб и ошибок) оказывается довольно долго и затруднительно – необходим хотя бы минимальный анализ исходных фигур. Для начала есть смысл просмотреть исходные фигуры и понять, есть ли среди них хотя бы две одинаковые. Оказывается, есть, значит можно попробовать поискать нераскрашенную фигурку такой же формы и размера. Такая фигурка отыскивается, значит именно ее нужно раскрасить в тот же цвет, что и две одинаковые фигурки.

Задача 107. Объектов здесь довольно много – может понадобиться перебор. Конечно, в первом задании перебор нужно вести только по русским буквам, а во втором – только по цифрам. Умение выделять из совокупности русские буквы для решения этой задачи является ключевым, поскольку здесь в наборе имеются пары одинаковых латинских букв. Если ученик выделил пару латинских букв, необходимо вернуться вместе с ним к листу определений «Русские буквы и цифры» и попросить его найти помеченные им в задании буквы в русском алфавите.

Задача 108. Прежде всего, ребенок должен внимательно прочитать условие задачи и понять, что от него требуется. Как видно, требуется найти круглую и квадратную бусины одного цвета. Задача облегчается тем, что квадратных бусин у нас всего три и все они синие. Значит, соединять надо синюю круглую бусину с одной из синих квадратных.

Задача 109. Необязательная. Здесь детям предстоит работать с реальными объектами – рукавицами, на которых нарисованы снежинки. Задача оказывается не слишком простой, ведь надо просмотреть каждую рукавицу и сравнить в ней снежинки между собой. При этом некоторые снежинки очень похожи и для такого сравнения требуется некоторое время. Так дети будут перебирать рукавицы, пока не отыщут искомую. С точки зрения понятий нашего курса данные объекты представляют собой мешки снежинок. Таким образом, в этой задаче мы ведем пропедевтику понятий «мешок» и «есть».