Информатика. 3–4 класс (часть 1) Демо+методичка

Урок 6. «Одинаковые (такая же). Разные»

Новые ключевые слова и выражения: одинаковые фигурки, разные фигурки, такой же (такая же).

Фигуркой в нашем курсе будет называться любой одиночный рисованный объект, т. е. любое изображение животного, фрукта, знака и т. п. Ребенок это усвоит в ходе решения большого числа задач с фигурками. Из фигурок впоследствии будут строиться более сложные объекты (цепочки, мешки, деревья). На этом уроке дети впервые знакомятся с основным свойством фигурок. Фигурки, как и многие другие объекты, могут быть одинаковыми и разными.

Одинаковость в разных случаях называется также тождеством, равенством, идентичностью, эквивалентностью. Она является одним из самых важных понятий математики и информатики. С одинаковыми предметами дети работали и в детском саду, понятие одинаковые кажется совсем элементарным, но это только на первый взгляд.

В информатике различные виды одинаковости приобретают особое значение. Ситуации здесь могут быть достаточно сложными, начиная с одинаковости приближенных чисел и кончая одинаковостью программ как функций из исходных данных в результаты (известно, что такая одинаковость для всех программ не может быть проверена никаким компьютером).

Дальше в наших учебниках будет определяться одинаковость различных объектов курса, но сейчас мы говорим об одинаковости фигурок. Вообще определение понятия одинаковые для любых объектов зависит от свойств, которые являются для этих объектов важными и определяют их как объекты данного вида. Так, отрезок полностью задается (характеризуется) своей длиной, а сигнал светофора - цветом. Однако бывают и гораздо более сложные случаи. Например, фигурки, являясь одновременно самыми простыми объектами для восприятия детей, обладают достаточно большим набором характеризующих их свойств. В частности, понятие одинаковые для фигурок сложнее, чем для обычных геометрических фигур на плоскости. Геометрические фигуры одинаковы в том случае, если они при наложении совпадают, поэтому для геометрических фигур важна только форма и размер. Для наших фигурок важен еще и цвет (или внутренняя раскраска), и расположение на листе. Действительно, как объекты, взятые из окружающего мира, фигурки несут в себе множество разнообразной информации, передающейся, в частности, цветом. Так, флаги государств отличаются исключительно внутренней раскраской. Кроме того, для многих фигурок важна ориентация относительно листа. Это очень хорошо иллюстрирует приведенный на листе определений пример со знаками дорожного движения.

Мы не стали давать словесное определение одинаковых фигурок, оно было бы слишком сложным. Однако все важные для фигурок свойства показаны детям на примерах, и из этих «кирпичиков» само собой сложится понятие одинаковости. Поэтому, чтобы описать свойства, важные для определения одинаковости фигурок, мы привели на листе определений также примеры разных фигурок, различающихся важными свойствами: цветом (раскраской), расположением на листе (в том числе симметричные фигурки), формой, размером.

Последний пример на листе определений показывает, что понятие одинаковые можно определять для любого числа фигурок в точности так же, как для двух. На первый взгляд может показаться, что это вполне естественно и не требует дополнительных договоренностей. Однако такая ситуация у нас в курсе (как и в информатике или математике) возникает далеко не со всеми понятиями. Например, понятие разные определяется для двух фигур достаточно просто - как не одинаковые. В то же время уже для трех фигур возникают сложности: можно определять разные как все неодинаковые (нет двух одинаковых) или как не все одинаковые (есть две разные). Отметим, что обе эти логические конструкции достаточно сложны, поэтому мы везде говорим только о двух разных фигурках.

Такой же

Мы используем два термина - такой же и одинаковый для одного и того же понятия (одинаковости). Дело в том, что по-русски нельзя сказать: «Вот фигурка. Найди здесь одинаковую фигурку», поэтому нам и приходится использовать два синонима для обозначения одного свойства.

Дискретизация

Дальше у нас будет встречаться много задач на клетчатой бумаге. Такие задачи бывают связаны с одним из важных понятий информатики - дискретизацией. Это понятие описывает ситуацию, когда имеется какой-то объект, например геометрическая фигура, или изображение, или звук, а мы хотим его описать более или менее точно с помощью цепочки букв и знаков - текста. Делать это можно по-разному. Можно сказать: «Вот тут, в углу, квадрат, а рядом что-то похожее на ухо». А можно разбить изображение на квадратики и перечислить подряд цвета квадратиков. Конечно, на границе цветов возникнет проблема: какого цвета там квадратик? Придется тем не менее выбрать какой-нибудь один цвет. Поэтому-то описание и становится приближенным. В жизни мы сталкиваемся с такой ситуацией довольно часто; например, мы измеряем что-то сантиметром и говорим: длина стола 108 см, а на самом деле она чуть больше - 108,1429... см.
108 - это приближение, дискретизация длины стола. Мы вышиваем крестиком картинку, переведенную по клеткам. Это дискретизация, и картинка получается дискретной. На экране телевизора изображение создается дискретными элементами. Дискретное (иногда говорят: оцифрованное, цифровое) представление информации становится все более и более распространенным.

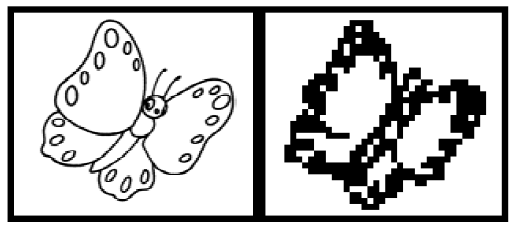
Вероятно, вы знаете, что любое изображение на экране компьютера именно такое - дискретное, составленное из мелких элементов. Эти элементы могут быть настолько мелкими, что человеческий глаз их не различает. Мы приводим здесь примеры компьютерных картинок - слева с совсем маленькими, а справа с довольно большими элементами. Посмотрите на правые картинки с расстояния 3 метров - дискретизация «исчезает»!

Решение задач из учебника

Задача 12 совсем простая: это проверка понимания определения. И в дальнейшем мы стараемся первую задачу после каждого листа определений сделать как можно более простой, чтобы ее решение просто показывало усвоение новой темы. С листом определений, который посвящен буквам, ребята знакомятся дальше, здесь же они оценивают одинаковость букв как фигурок. 

Задача 13. Здесь нужно преодолеть ступеньку, которая вам может показаться совсем незначительной: надо что-то сделать, построить, сконструировать. Интересно, что хотя можно описать раскраску с помощью номеров клеток: «Первую, третью, пятую клетку...», но и вы сами, и дети будут пользоваться другими терминами. Тем не менее задачу эту, скорее всего, решат все, кто разобрался с определением. Это надо тщательно проверить. Как и многие другие задачи в начале курса, она открывает серию задач, среди которых имеются важные и сложные.

Задача 14. Задача на повторение. Работа над ней поможет вам понять, как ребята усвоили, что такое область. Действительно, условие задачи содержит ловушку для тех учащихся, которые до сих пор выделяют области по смыслу, а не по договоренности, принятой на листе определений. Такие учащиеся увидят в картинке всего 2 области - звезду и фон, и вся картинка у них окажется раскрашенной. С такими учащимися придется вернуться к предыдущему листу определений, ведь на самом деле в данной картинке 8 областей.

Задача 15. Необязательная. Эта задача несколько сложнее, чем задача 12, так как требуется найти три одинаковые фигурки.

Компьютерный урок «Одинаковые (такая же), разные. Соедини»

Лист определений «Соединяем линией»

Как видите, на данном компьютерном уроке вводится действие «соедини», в то время как в учебнике оно вводится только на следующем уроке. Поэтому если обычно мы не настаиваем на просмотре компьютерных листов определений (поскольку дети могут знакомиться с ними по учебнику), то в этом компьютерном уроке изучение первого листа определений - обязательно для всех учащихся. Если при решении компьютерных задач учащийся будет нарушать правила игры, нужно посоветовать ему еще раз обратиться к компьютерному листу определений. Подробно о правилах действия «соедини» см. в комментарии к следующему уроку.

Решение задач

Задача 15. Цель этой задачи – познакомить ребят с новым инструментом. По содержанию задача совсем простая, но дети, возможно, потратят на нее достаточно много времени: редкий ребенок проводит нужную линию с первого раза. Наибольшие проблемы вызовет прерывистость линии. Карандаш начинает рисовать линию в месте первого нажатия кнопкой мыши и рисует ее до тех пор, пока ребенок не отпускает кнопку. Ребенку сложно одновременно смотреть на экран и следить за нажатием кнопки, поэтому он отпускает мышь преждевременно. При попытке продолжить дальше начатую линию со второго щелчка у детей редко получается аккуратно, но если линия не имеет разрывов, то это вполне допустимо. Приготовьтесь к тому, что ребятам понадобится не одна попытка, прежде чем им удастся выполнить задание. В этой задаче мы предлагаем ребятам удалять линию, используя кнопку отмены. Если у кого-то на рисунке оказалось несколько линий, посоветуйте ему воспользоваться кнопкой «сначала» или в индивидуальном порядке научите прицеливаться в линию ластиком.

Задача 16. Здесь надо не просто нарисовать линию, а соединить линией. Поэтому должны выполняться все договоренности компьютерного листа определений «Соединяем линией». Кроме того, желательно (хотя и необязательно), чтобы линия не пересекала другие фигурки на экране. Детей с хорошей координацией можно попросить об этом в индивидуальном порядке. Остальных ребят можно попросить об этом в следующих задачах, когда они лучше освоятся с новым инструментом.

Задача 17. Здесь фигурок на экране больше и они более мелкие, чем в предыдущей задаче. Поэтому от ребят потребуется несколько большее мастерство в использовании карандаша.

Задача 18. Данная задача как содержательно, так и инструментально сложнее трех предыдущий. Поскольку объектов в этой задаче много, от ребят требуется аккуратность, чтобы не перечеркивать своей линией данные в задаче объекты (это не обязательно, но желательно). С точки зрения содержания, данная задача поддерживает курс математики, поскольку в ней дети имеют возможность повторить названия и написание цифр. Если курс информатики ведет не основной учитель, желательно перед данным уроком уточнить у основного учителя, повторялись ли цифры, используемые в задаче в курсе математики.

Задача 19. В данной задаче дети повторяют понятие «область». Как уже говорилось, в компьютерных задачах выделение и заливка областей производится автоматически правильно. Если вы предлагали на предыдущем уроке детям кроме компьютерных и бумажные задачи на выделение областей, можно попросить ребят сначала решить эту задачу на бумаге (предварительно распечатав ее), а потом проверить свое решение на компьютере. В данной картинке всего три области и все они оказываются раскрашенными в результате решения задачи.

Задача 20. Эта задача немного сложнее предыдущей - в ней больше областей. Ее на бумаге можно предложить решать только наиболее подготовленным учащимся. В данном случае в картинке 8 областей, из которых в результате решения 2 останутся нераскрашенными.

Задача 21. Уровень сложности данной задачи обусловлен не только большим числом областей (здесь их 10, не считая маленьких областей глаз и носа), но и трудностью их выделения. Действительно, здесь области не везде соответствуют деталям рисунка. Кроме того, есть довольно большие области, которые трудно охватить взглядом и очень маленькие области, которые легко не заметить. Поэтому данную задачу можно предложить на бумаге только самым сильным ученикам.

Задача 22.. Областей в картинке много, эта задача потребует от ребенка терпения и аккуратности. Поскольку в задаче не накладывается никаких условий на раскрашивание, любое решение следует считать правильным. Но, скорее всего, вы встретите у ребят решения двух видов, назовем их «формальное» и «художественное». Формальное решение выполняется только в соответствии с правилом раскрашивания и допустимыми цветами. Поскольку обе договоренности в компьютерной задаче выполняются автоматически, такое решение будет для ребенка несложным. Так ребенок может раскрасить области в любые цвета, по типу мозаики. Художественное решение состоит в том, чтобы следовать не только нашим правилам, но и содержанию рисунка. Повторим, по нашим правилам это не требуется, но опять-таки в силу формулировки задания (раскрась какими хочешь цветами) мы не можем этого запрещать детям. Так многие дети захотят выделить на картинке слона и раскрасить все относящиеся к нему области одним цветом. Это потребует при решении дополнительного времени, поскольку в силу мозаичности картинки сделать это будет не так-то легко.

Задача 23. В этой задаче есть две разные кошки, отличающиеся только расположением на листе (они зеркально симметричны). Если кто-то из детей рассмотрел лист определения невнимательно, он может соединить именно этих кошек. Такого ребенка следует вернуть на второй экран листа определений (примеры в правой части).

Задача 24. Эта задача сложнее предыдущей. Первая сложность в том, что фигурок гораздо больше. Вторая - в том, что фигурки довольно похожие, причем не раскрашенные, поэтому при поиске никак не помогает цвет. Несмотря на использование букв русского языка, эта задача больше относится к информатике, поскольку предполагается, что дети будут анализировать буквы просто как фигурки. В данном случае дети должны раскрасить две одинаковые буквы Ч.

Задача 25. Правильных ответов (пар животных) здесь довольно много. Чаще всего ошибаются в таких задачах дети невнимательно прослушавшие задание или те, которые просто путают слова одинаковые/разные.

Задача 26. Эта задача начинает новую серию задач на построение фигурки такой же, как данная. Проще всего решать такие задачи, по очереди двигаясь по квадратикам обеих фигурок, раскрашивая квадратики нераскрашенной фигурки по образцу. Например, можно двигаться по квадратикам слева направо и сверху вниз. Конечно, это только одна из стратегий. Ребята могут придумать и другие, не столь формальные и поэтому не гарантирующие правильности решения. Поэтому в таких задачах особенно внимательно нужно отнестись к проверке – по окончании решения каждый ребенок должен убедиться в том, что построенные фигурки действительно одинаковые.