Информатика. 4 класс Демо+методичка

Уроки 19 – 20. «Робик. Цепочка выполнения  программы»

Элементы цепочки выполнения программы – позиции Робика. На самом деле это не такое уж существенное новшество. Дело в том, что, во-первых, мы и не говорили раньше, что что-то не может быть бусиной цепочки. Во-вторых, позиция – это фигурка, и она во многих случаях может считаться просто символом специального алфавита. В-третьих, и саму позицию нетрудно представить в виде цепочки. Например, в нашем случае можно выписывать последовательно все клетки в качестве бусин (эти бусины будут различаться окраской и наличием/отсутствием Робика). Последовательность бусин в этой цепочке можно фиксировать по-разному, например, как последовательность букв на странице книги.

Цепочка выполнения программы играет важную роль в самых разных конструкциях информатики и теоретической, и практической. Она представляет собой статический (неподвижный, неизменный) объект, являющийся как бы видеозаписью динамического процесса выполнения программы (как, например, раскадровка мультфильма). Переход к такому статическому объекту  помогает нам разобраться в работе программы. Часто рассматривается не одна цепочка выполнения команд, а множество таких объектов в случае, если ход выполнения программы не определен полностью исходными данными или если мы одновременно рассматриваем выполнение программы при различных исходных данных.

Цепочка выполнения программы напоминает цепочку позиций игры. Можно обсудить с детьми, какую они видят разницу и какое сходство в этих цепочках. В обсуждении может возникнуть вопрос о том, кто и на каком основании делает, т. е. выбирает, очередной ход (в случае цепочки позиций игры выбор делают  игроки на основании правил игры, а в цепочке выполнения команд «выбор» основан на последовательности команд программы).

Решение задач из учебника

Задача 105. Задача, которая поможет детям усвоить новый материал.

Ответ:

Задача 106. Задача, обратная предыдущей, помогающая усвоить материал листа определений.

Ответ:

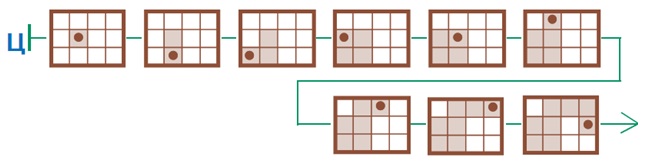
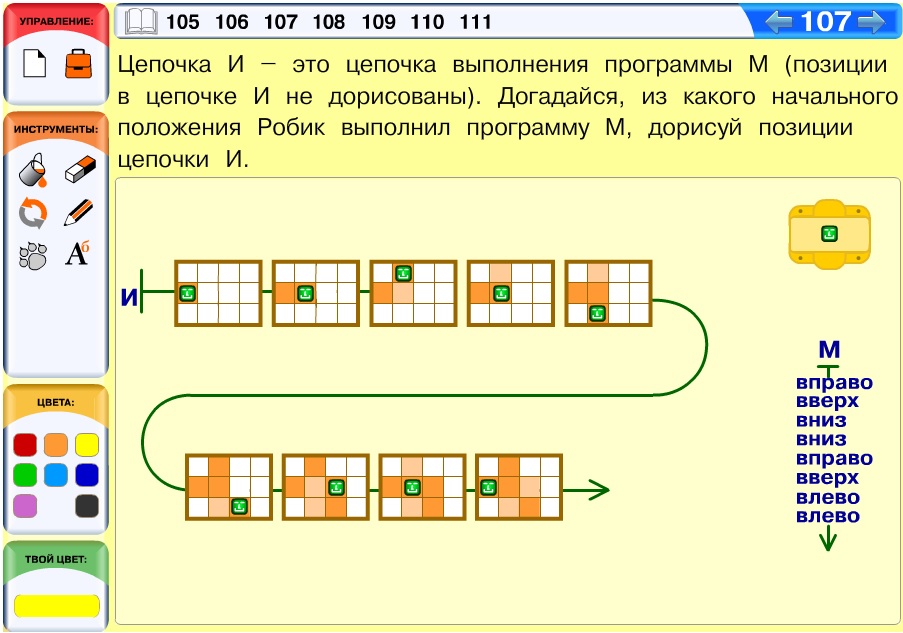
Задача 107. Это одновременно упражнение на закрепление нового листа определений и задание на выполнение программы для Робика с неизвестным начальным положением (подобные задачи уже были раньше). Главное здесь – определить, из какой клетки начал движение Робик. Для этого можно воспользоваться одним из подходов, знакомых детям еще из 2 части курса: либо последовательно проверять все клетки поля как возможные начальные положения, отбрасывая при этом неподходящие (например, вычеркивая их), либо выполнить программу на клетчатой основе и заштрихованную Робиком фигуру поместить в поле. Поскольку в данном случае поле – прямоугольник, то второй подход делает решение задачи совсем простым. Поэтому второй подход можно посоветовать слабому ученику, если он запутался. Остальных детей лучше, как всегда, «отпустить в самостоятельное плавание».

Особенностью данной задачи является прямоугольное поле, значит, возможность, например, горизонтального движения Робика не зависит от вертикального движения. Поэтому можно отдельно устанавливать начальное положение по командам вверх-вниз и вправо-влево. Например, цепочка команд по вертикали «вниз, …, вверх,…, вверх, ..., вниз» позволяет сделать вывод, что в начальный момент Робик находился на второй строке. А цепочка команд по горизонтали «..., влево, ..., вправо,…, вправо, вправо,…» говорит о том, что Робик начал движение в клетке второго столбца. Теперь задача становится совсем простой – надо вырезать из листа вырезания и наклеить в цепочку столько полей, сколько команд в программе (ведь одно поле для начальной позиции уже есть), и раскрасить клетки.

Ответ:

Задача 108. Эта задача «с подвохом». Поскольку начальная позиция нечетная и все разрешенные ходы нечетные, то после любого хода Первого позиция будет четной, после любого хода Второго – нечетной. Таким образом, в данной игре всегда будет выигрывать Первый. По сути дела, выигрышная стратегия Первому вообще не нужна, однако это не значит, что ее нельзя найти формально. Дети, скорее всего, не заметят необычности данной задачи и начнут решать ее по знакомому алгоритму:

1. Раскрасят числовую линейку:

2. Заметят, что все проигрышные позиции – четные числа, а выигрышные – нечетные числа.

3. Запишут выигрышную стратегию формально – Первый должен на каждом своем ходу забирать столько камешков, чтобы Второму досталось четное число.

Лишь некоторые учащиеся поймут, что в игре не может победить Второй. С такими ребятами по окончании решения мы советуем провести обсуждение этого вопроса. Следует обратить внимание на то, что существуют игры, когда у игроков просто нет выбора (например, игры камешки с ходом 1), в этом случае выигрышная стратегия не нужна. 

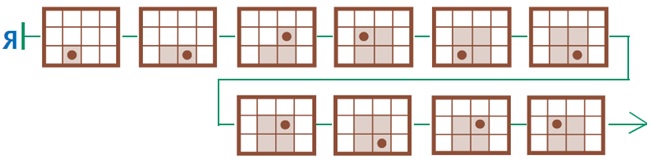
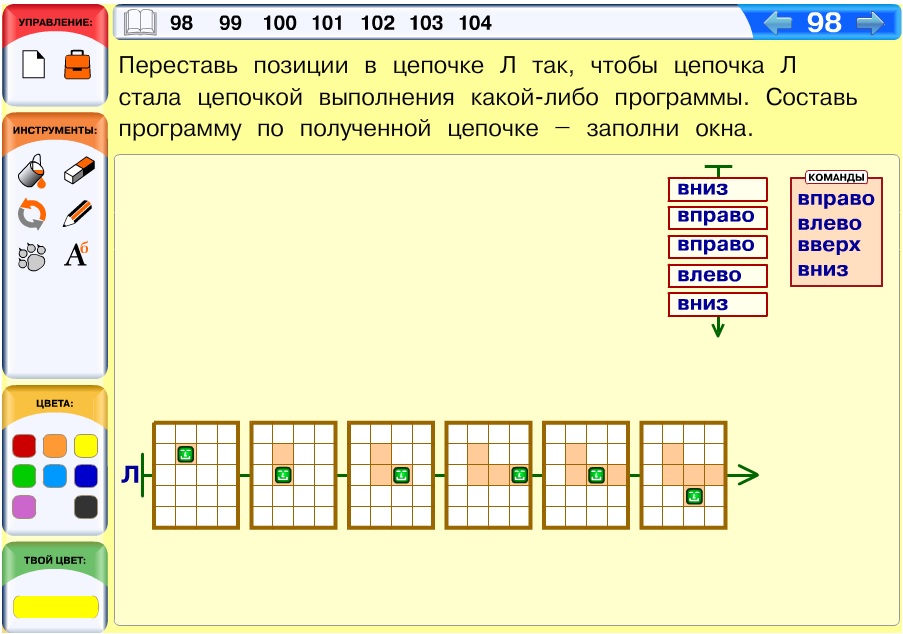
Задача 109. Эта задача по содержанию продолжает серию заданий про Робика, но ее формулировка будет для ребят новой. Поэтому кто-то из учеников может даже не разобраться, что здесь имеется в виду. Обсудите с ребятами, что цепочка Я пока не является цепочкой выполнения программы, и бусины цепочки Я пока нельзя назвать позициями Робика: в них раскрашены не все нужные клетки, нет жирной точки, указывающей, в какой клетке находится Робик. С другой стороны, некоторые клетки в бусинах цепочки все же раскрашены, и нужно это учесть – «стереть» раскраску мы не можем.

Во всех предыдущих задачах программа и поле Робика однозначно задавали начальную позицию. Самым главным было найти эту клетку. В данной задаче ситуация иная: Робик может выполнить программу Ю, стартуя из разных клеток поля. Поэтому для нахождения единственного решения требуется дополнительная информация. Эта информация заложена в раскрашенных клетках бусин цепочки Я.

Несмотря на новизну формулировки, одна из идей, помогавших при решении подобных задач ранее, может здесь пригодиться. Достаточно запустить Робика на любом листе клетчатой бумаги – и мы увидим, что он путешествует только по квадратику из четырех клеток. Цепочка Я легко позволяет найти эти четыре клетки. При этом Робик начинает выполнение программы из левого нижнего угла этого квадратика.

Теперь ребятам останется лишь аккуратно раскрасить каждую позицию в соответствии с командами программы.

Ответ:

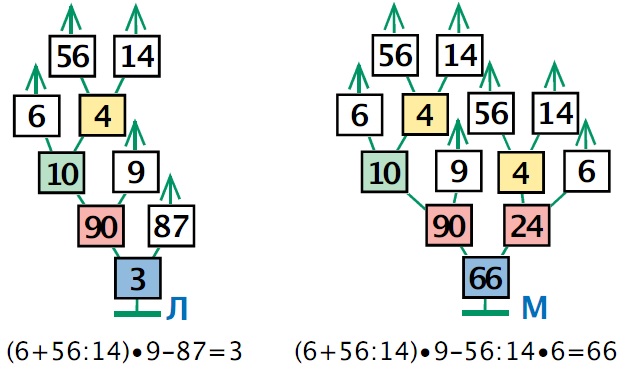
Задача 110. Эта задача того же типа, что и задачи 99, 100. С точки зрения арифметики, здесь ситуация даже несколько проще, ведь в задачах 99 и 100 встречаются двойные вложенные скобки. Но структура представленных в этой задаче деревьев сложнее – больше уровней, больше листьев на разных уровнях.

Ответ: 

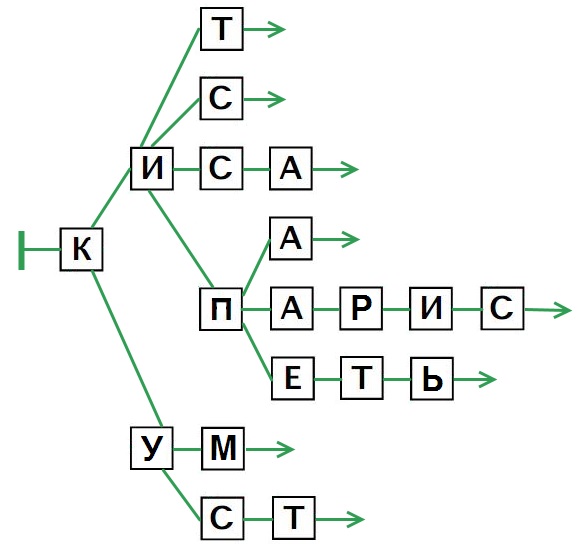
Задача 111. Ребятам уже встречалась подобная задача (см. комментарии к задаче 18). Здесь так же, как и в задаче 18 нужно экономить вершины, то есть не размещать на одном уровне две одинаковые вершины, имеющие общую предыдущую (или две одинаковые вершины первого уровня). Исключение из этого правила составляет лишь случай, когда одна из одинаковых вершин является листом, а другая – нет. Например, в мешке V есть слова КИС и КИСА. У этих путей будет две общие вершины – К и И. Однако бусины С этих путей будут разными вершинами дерева.

Вариант решения:

Задача 112. Эта задача продолжает серию задач на сочетание кванторов – все, каждый, есть. То, что в качестве простейших свойств объектов используются свойства, формулируемые с помощью наших понятий, относящихся к словам и буквам, не так уж важно. Важнее именно логическая структура предложения, представленная здесь мешками, словами каждый, найдется. Эта структура будет одной и той же независимо от того, работаем ли мы с числами, геометрическими фигурами, программами или словами.

При решении ребята могут столкнуться с двумя трудностями. Во-первых, в формулировке фигурируют два вида мешков: мешки мешков («внешние» мешки) и мешки со словами («внутренние» мешки), которые обозначены одним и тем же словом – мешок. Кто-то из ребят может запутаться, где какой мешок имеется в виду. В этом случае можно прямо в условии сделать пометки «внешний» и «внутренний» или «большой» и «маленький».

Во-вторых, достаточно сложной может оказаться логическая структура высказывания, поскольку содержит два квантора: для каждого (для любого) и есть (существует, найдется). Если кому-то из ребят трудно сразу понять эту структуру, то рассуждайте вместе с ними. Проще всего понять смысл условия, относящегося к отдельным словам мешков. Наверняка каждый ребенок вам скажет, что мы будем искать такие слова, первая и последняя буквы которых одинаковы. А теперь ваша задача – обратить внимание ребенка на главные слова высказывания: есть и каждый. Например, можно спросить: «Сколько таких слов мы должны найти в каждом внутреннем мешке?» Ответ на этот вопрос побудит ребенка обратиться к формулировке, выделить в ней слово есть – значит, найдется хотя бы одно. Итак, мы поняли, что нужно искать внутренний мешок, содержащий хотя бы одно слово, первая и последняя буквы которого одинаковые. Чтобы довести рассуждения до конца, спросите: «Сколько в большом мешке должно быть мешков с нужным нам словом: один, два или три?» Читая условие, ребенок обязательно обратит внимание на слово каждый. Это означает, что все три внутренних мешка должны содержать необходимые слова. После серии таких вопросов каждый ребенок будет знать, что делать, и без труда найдет мешок, в данном случае – мешок S.

Задача 113. Необязательная. В данной задаче ребятам необходимо помнить не только то, что такое путь дерева, но и то, какое число называется нечетным. Возможно, кому-то придется напомнить, что нечетным  мы называем число, которое не делится на 2. Если учесть число уровней дерева Y, подходящие нам пути могут иметь длину 1, 3 или 5. Путей длины 1 в дереве Y нет. При поиске путей длины 3 и 5 сильно помогает то, что дерево нарисовано по уровням. Поэтому можно просто пометить все листья, находящиеся на третьем и пятом уровнях (их 10), а затем выписать все пути, ведущие в эти листья. Это лишь один из способов решения задачи, ребята, скорее всего, будут использовать самые разные стратегии решения. Однако стоит обратить внимание на то, что в задаче необходимо выписать все пути, удовлетворяющие условию, поэтому какая-либо стратегия перебора нужна в любом случае.

Ответ:

Задача 114. Знакомое детям задание о заполнении двумерной таблицы для мешка. Особенностью данной задачи является ее геометрическое содержание, а именно форма фигурок. В мешке, кроме привычных круга, треугольника и квадрата, лежат еще правильные многоугольники: пяти-, шести-, семи- и восьмиугольники. Обсудите с учащимися, как отличить многоугольники друг от друга. Если ребенок запутался, попросите его посчитать и распределить по формам сначала все желтые фигуры, затем красные и т. д.

Заполнив таблицу, полезно убедиться в том, что общее число фигурок в таблице и в мешке одинаковое. Совпадение этих результатов, как известно, является необходимым, но не достаточным условием правильного решения. Эта процедура может послужить первым этапом проверки, выявляющим вычислительные ошибки или ошибки, сделанные из-за невнимательности. Вторым этапом является сравнение непосредственно результатов подсчета для каждой клетки в таблице. Проверку можно организовать как в парах, так и в группах. Ребятам, которые справились быстро, можно посоветовать самостоятельно проверить свои результаты, ориентируясь на столбцы (если считали по строкам), или наоборот.

Ответ: 

Задача 115. Попробуем собрать искомую цепочку из частичных решений (эта идея работала в аналогичных задачах раньше). Из первого утверждения становится ясно, что в искомой цепочке будет два кусочка А – З. Букв У в задаче три, значит из второго утверждения следует, что в цепочке должно быть три кусочка вида У – …  – Д. Для этого нужно 9 букв, а у нас осталось только 7, значит собрать эти кусочки независимо друг от друга не получится – частичные решения придется склеивать. Так рождается идея составить кусок УУДД, где соединены вместе два частичных решения. 

Задача 116. Необязательная. Аналогичные задачи ребятам уже встречались (см. комментарии к задаче 104). Разные ребята будут действовать в этой задаче по-разному. Одна из идей заключается в том, чтобы разбить слова на группы по наличию или отсутствию некоторой буквы. Если некоторая буква встречается только в одном из слов, его можно сразу вычеркнуть. Так можно сразу вычеркнуть слово КОФЕЙНИК, поскольку только в нем встречается буква «Й», слово ЖЕРЕБЧИК (из-за буквы Б), слово ВКЛАДЧИК (из-за буквы Д). Остальные слова можно разделить на две группы по наличию или отсутствию буквы «А». В одной из групп при этом остаются два слова с одинаковыми мешками букв – ИСТОПНИК и СИНОПТИК.

Компьютерный урок «Робик. Цепочка выполнения программы», часть 1, задачи 98 – 104

Задача 98. На первый взгляд задача очень похожа на аналогичные задачи про цепочку игры. Однако эта задача сложнее. Действительно, в задачах о цепочке игры в крестики-нолики несложно было ориентироваться по числу ходов на поле. В задачах же о цепочке выполнения программы Робик может неоднократно проходить по одним и тем же клеткам, поэтому в результате очередного хода число закрашенных клеток может и не увеличиться. Таким образом, здесь не получается решить задачу формально, нужен некоторый анализ программы.

В нашей цепочке есть ровно 1 позиция с одной закрашенной клеткой, 1 позиция – с двумя закрашенными клетками и 1 – с тремя. Они и будут соответственно первой, второй и третьей позицией нашей цепочки. Дальше дело обстоит сложнее – у нас есть две позиции с четырьмя закрашенными клетками. Какая из них будет четвертой, а какая – пятой позицией цепочки? Чтобы это выяснить, лучше начать составлять программу по первым трем уже известным позициям. После этого станет понятно, в какой клетке был Робик перед выполнением четвертой команды, и можно будет понять, какая команда (и позиция) четвертая, а какая – пятая. Оставшаяся позиция будет последней.

Ответ: 

Задача 99. Самый первый шаг в решении этой задачи – выяснить положение Робика в начальной позиции. Это не слишком сложно, поскольку среди закрашенных клеток имеется лишь одна, из которой можно выполнить две команды «вправо» (две первые команды программы Т). После того как нужная клетка найдена, построить решение уже просто.

Ответ: 

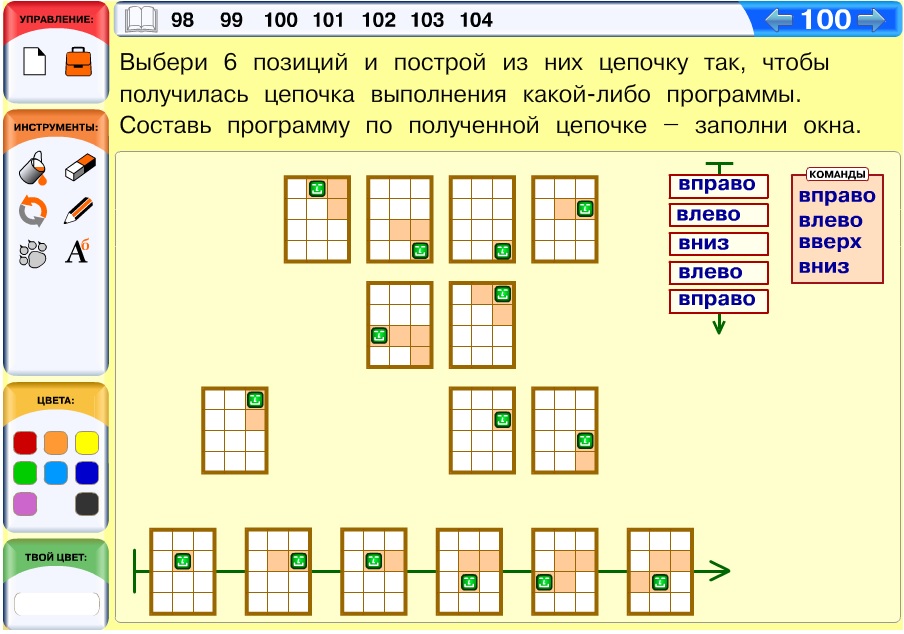
Задача 100. Сложная задача, предназначенная в основном для сильных учащихся. В отличие от аналогичных задач о построении цепочки игры (см. комментарии к компьютерным задачам 9, 10), здесь трудности возникают даже с определением заключительной позиции. Число закрашенных клеток в этом смысле нам не слишком помогает, ведь Робик может на протяжении всей программы двигаться с повторениями клеток. Поэтому здесь не удается оттолкнуться от заключительной позиции. Приходится начинать работать с начальными позициями и разбирать все возможные цепочки программ. В процессе перебора дети начнут улавливать закономерности и строить перебор более осознанно.

Ответ: 

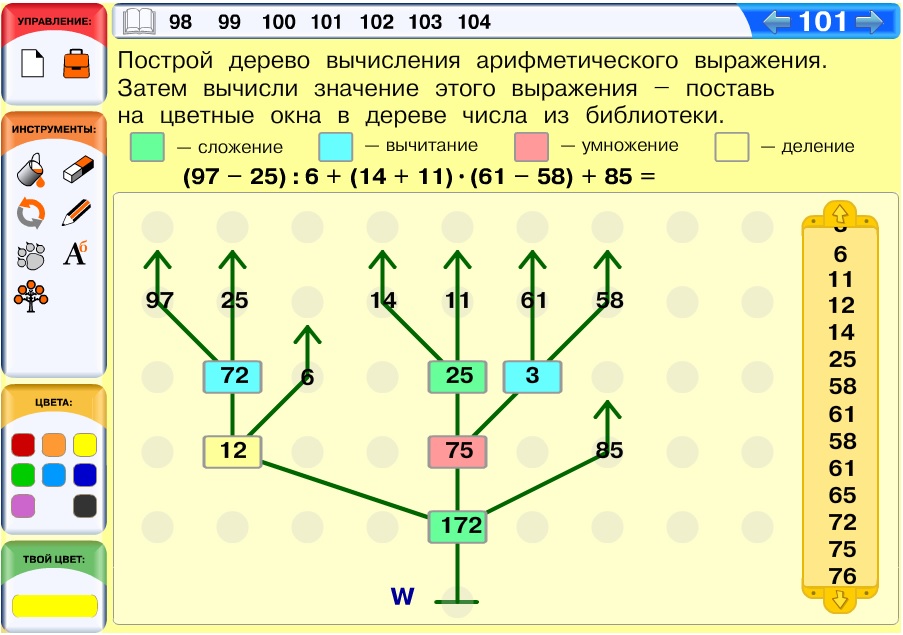
Задача 101. Задача о построении дерева арифметического выражения. Но в отличие от предыдущих аналогичных компьютерных задач, здесь нужно не только построить дерево, но и вычислить значение арифметического выражения с помощью этого дерева.

Вариант ответа: 

Задача 102. В этой задаче ребята повторяют упорядочивание слов в словарном порядке. Слова подобраны так, чтобы ребятам пришлось использовать правило упорядочивания слов с одинаковым началом – по 6–7 букве.

Ответ:

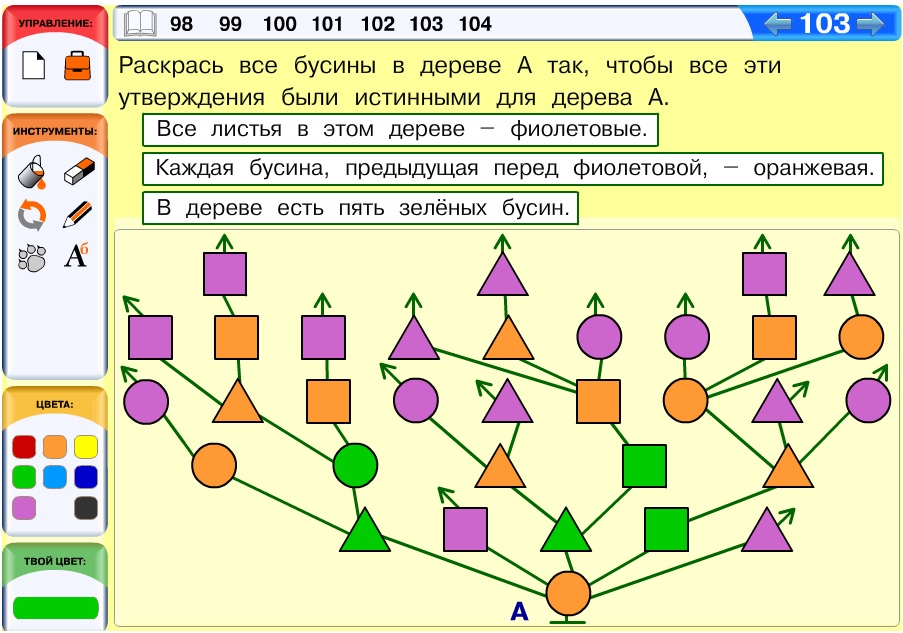
Задача 103. Повторение понятий все, каждый, есть – нет и применение их для бусин в дереве. После того как все листья будут раскрашены фиолетовым и все бусины перед листьями – оранжевым, в дереве останется 5 нераскрашенных бусин – эти бусины и нужно будет раскрасить зелёным.

Ответ: 

Задача 104. Сложности в таких задачах возникают обычно у тех детей, которые пытаются раскрашивать одновременно с разных концов картинки. Лучше всего начинать раскрашивать с одной области, которая граничит с тремя областями, и двигаться от нее ко всем другим областям. Например, мы раскрасили красным один из треугольников (или криволинейных треугольников) в центре. Тогда три соседние области нужно раскрасить в три разных цвета: желтый, синий, зеленый. Дальше раскрашиваем соседние с уже раскрашенными области, на каждом шаге проверяя, не появились ли две соседние области, раскрашенные в один цвет. Если не появились – продолжаем раскрашивать дальше. Если появились, возвращаемся на шаг назад.

Компьютерный урок «Робик. Цепочка выполнения программы», часть 2, задачи 105 – 111

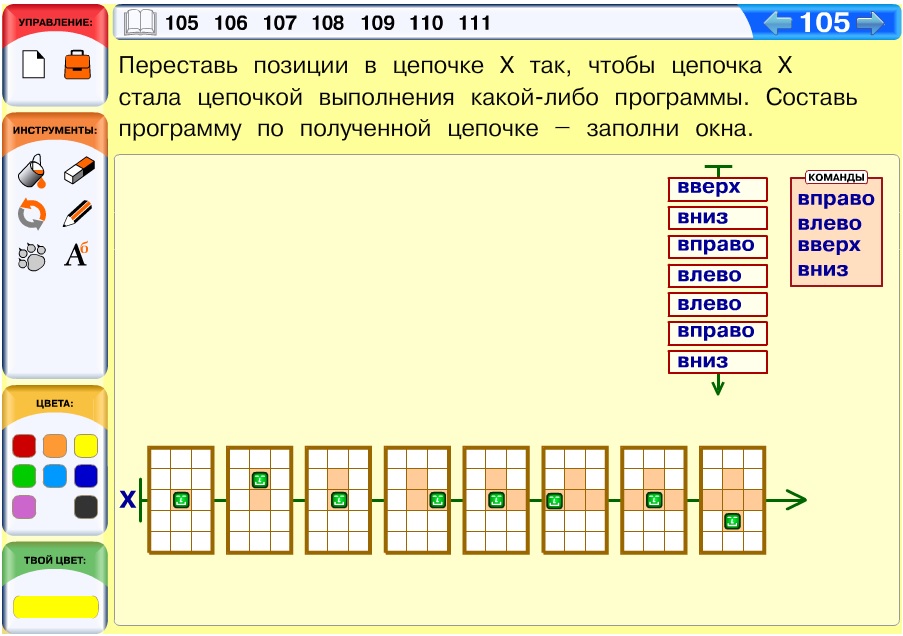
Задача 105. Как и задача 98, эта задача не очень простая.

Ответ: 

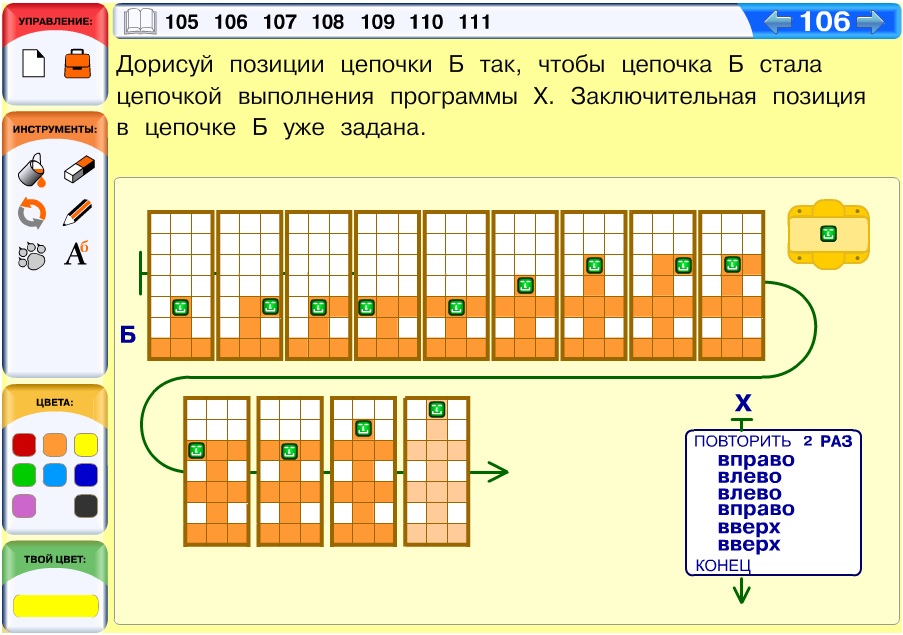
Задача 106. В этой задаче есть один нюанс, который может поставить некоторых детей в тупик. На первый взгляд все просто – по программе Робик должен всего выполнить 12 команд, в цепочке 13 позиций, а на поле 13 раскрашенных клеток. И сначала кажется, что Робик за каждую команду раскрашивал по одной клетке. На самом деле ситуация здесь обстоит совсем не так. Как только мы начинаем анализировать программу, мы понимаем, что Робик в процессе ее выполнения неоднократно проходил по одним и тем же клеткам. А поскольку всего на поле раскрашено 13 клеток, значит, в начальный момент некоторые клетки уже были раскрашены. Чтобы до этого догадаться, достаточно выполнить 1 раз все внутренние команды конструкции повторения и посмотреть, что за рисунок получится. Видим, что таких орнаментов в последней позиции три. Значит, два орнамента Робик нарисовал в процессе выполнения программы, а один на поле уже был в начальной позиции.

Ответ: 

Задача 107. Так же как и предыдущая задача, эта задача о построении цепочки выполнения программы, но только более сложная. Здесь не заданы начальная и заключительная позиции Робика, но закрашены некоторые клетки поля, в которых Робик обязательно должен «побывать» хотя бы один раз. Решение можно немного упростить, если предварительно собрать все заданные закрашенные клетки на одном поле:

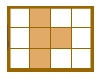
Сопоставив этот рисунок с программой, заметим, что при выполнении последовательности команд вверх – вниз – вниз – вправо – вверх Робик закрасит нужные клетки. Останется проверить, есть ли у Робика возможность выполнить остальные команды программы – первую команду вправо и две последние команды влево. Оказывается, такая возможность есть.

Ответ: 

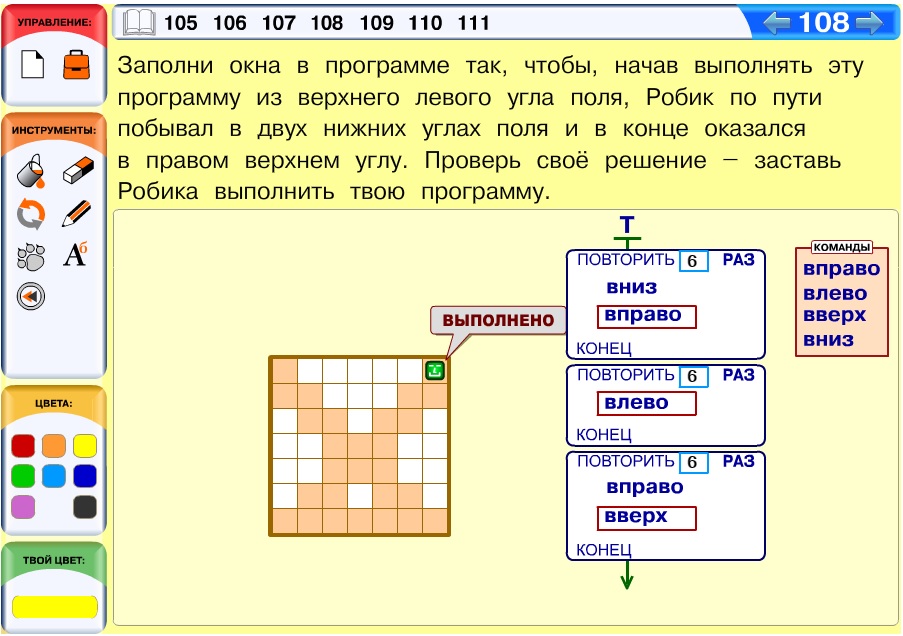
Задача 108. Если не обращать внимания на заготовку программы, для решения задачи Робику достаточно было бы пройти по границе поля до конца вниз, затем до конца вправо, затем до конца вверх. Но в программе в третьем цикле стоит команда «вправо». Это значит, что после выполнения первых двух циклов Робику необходимо оказаться как минимум не вплотную к правой границе поля. А лучше – в левом нижнем углу. Тогда недостающая команда в третьем цикле будет команда «вверх». Дальше уже все понятно: в результате выполнения первого цикла Робик должен оказаться в правом нижнем углу – команда в окне должна быть «вправо». А во втором цикле команда – «влево».

Ответ: 

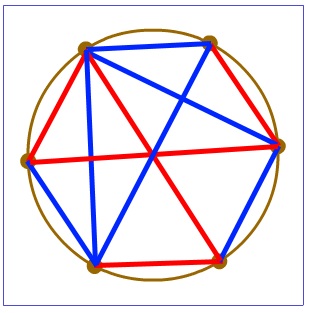
Задача 109. Повторение правил игры сим. Наиболее простой способ решения этой задачи – сыграть с товарищем партию в сим на бумаге, а затем перенести заключительную позицию на экран. Или играть «самому с собой» и поочередно рисовать отрезки синим и красным. По окончании игры попросите ребят обязательно провести проверку выполнения всех правил игры и того факта, что позиция получилась действительно заключительной.

Ответ: 

Задача 110. Хотя все объекты в задаче напоминают календарные даты, но не все являются таковыми. Для начала надо отобрать существующие даты. После этого задача становится несложной.

Задача 111. Эта задача больше развлекательная. Можно проверять все три условия для каждого гнома в отдельности. А можно пойти другим путём, например, вычёркивать сначала гномов в красной шапке, потом – в зелёных штанах, и наконец, тех гномов, у которых фиолетовая рубашка. Оставшихся гномов и нужно будет пометить синей галочкой.

Ответ: