Информатика. 4 класс Демо+методичка

Уроки 17 – 18. «Дерево вычисления»

Многие структуры, изучаемые в нашем курсе (например, цепочки или мешки), являются не чисто информатическими, а универсальными: эти понятия используются в других школьных предметах, в науке, применяются в производстве, встречаются в обыденной жизни. Понятие дерева в этом плане не является исключением. «Древесная» структура помогает в случае, когда объект (процесс, класс предметов и т. д.) на каждом шаге распадается на несколько объектов (возможностей, подвидов и т. д.). Поэтому с помощью дерева можно организовать эффективный перебор вариантов возможных партий игры (дерево игры), строить различные классификации и родословные (фамильные) деревья. На данном листе определений ребята знакомятся еще с одной областью применения деревьев. С помощью деревьев удобно изображать процесс вычисления значения арифметического выражения, ведь в результате каждого арифметического действия с двумя числами получается одно число, которое на следующем шаге также служит компонентом некоторого действия. Так постепенно можно двигаться от одной ступени действий к другой, руководствуясь правилами порядка действий, и дойти до результата. Естественно представить подобный процесс в виде дерева, где листья – числа, входящие в пример, а общая предыдущая вершина для двух листьев – результат выполнения некоторого действия. Далее с полученными результатами можно делать аналогичным образом следующие действия, постепенно доходя до корневой вершины – значения выражения.

Примерно так же в виде дерева можно представить процесс приготовления кулинарных блюд, где постепенное соединение ингредиентов по парам или группам (и их последующее смешивание, варка, жарка и пр.) приводит на каждом шаге к появлению одного полуфабриката, а в итоге к появлению некоторого блюда. Аналогично можно представить процесс сборки различных механизмов и т. п.

Дерево вычисления имеет и свои отличия от тех деревьев, с которыми ребятам приходилось работать раньше. Первое из них состоит в том, что обычно, работая с деревьями (строя или анализируя), ребята двигались от корневой вершины к листьям. Здесь же естественный порядок построения и исследования дерева обратный: от листьев к корню. Вторая особенность дерева вычислений состоит в том, что раньше ребятам чаще всего нужно было проследить по дереву только какой-то один путь (или несколько), теперь для вычисления значения выражения непременно надо «пройти» по всему дереву, не пропустив ни одной вершины.

Еще одна особенность дерева вычисления – необходимость дополнительной информации: для каждой пары чисел нужно указать, какую именно арифметическую операцию надо выполнить с этими числами, иначе дерево не будет содержать необходимую для вычисления значения выражения информацию. Эту дополнительную информацию по договоренности можно обозначить самыми разными способами. Мы выбрали, на наш взгляд, самый простой и однозначно воспринимаемый способ – раскраску вершины-результата в соответствующий цвет. Это вопрос общей договоренности, поэтому от ребят не требуется запоминания обозначений цветов действий. В задачах мы всегда будем использовать одну и ту же раскладку цветов (сложению будет соответствовать зеленый, вычитанию – синий, умножению – красный, делению – желтый цвет). Мы используем бледные оттенки этих цветов, чтобы числа, написанные в цветных окнах, выделялись четко. В каждой задаче, посвященной деревьям вычислений, будет помещена раскладка цветов (в задачах 92 – 95 дети будут пользоваться раскладкой, приведенной на листе определений). В дальнейшем появятся и задачи на самостоятельное построение дерева вычислений. В такой задаче учащемуся придется самостоятельно создать раскладку цветов, и такая раскладка совсем необязательно должна будет совпадать с той, которая приведена на листе определений.

До сих пор мы не упорядочивали вершины внутри уровня дерева – не говорили о первой, последней или левой–правой вершинах третьего уровня и т. п. Но в дереве вычислений мы будем по возможности следить за тем, чтобы общий «горизонтальный» порядок листьев был таким же, как в заданном арифметическом выражении: если какое-то число идет в выражении раньше другого, то и в дереве оно должно стоять левее (хотя, быть может, и на другом уровне). И это еще одна отличительная особенность дерева вычислений. Важно соблюдать это правило при работе с арифметическими действиями, не обладающими переместительным свойством, – вычитанием и делением. При обсуждении листа определений обязательно обратите на это внимание ребят. Чтобы не перегружать лист определений сложными текстами, мы не стали писать об этой договоренности вычитать и делить слева направо, просто именно так мы всегда будем поступать. 

Решение задач из учебника

Задачи 92 и 93. Впервые в курсе встречаются задания, которые несут вычислительную нагрузку. Естественно кому-то из ребят это понравится, кому-то нет. Для учителя такие задания могут стать хорошим поводом для организации интегрированных уроков с уроками математики – занятий на отработку вычислительных навыков. В дальнейшем подобные задания можно использовать на уроках математики для упражнения в устном счете. Мы старались, чтобы вычисления, необходимые при решении подобных задач, были нетрудными: ведь основная нагрузка задания состоит не в том, чтобы вычислить значение выражения, а в том, чтобы научиться правильно работать с деревом вычислений.

В данных задачах от ребят требуется только заполнить цветные окна дерева – вычислить и записать в соответствующие окна значения арифметических действий. Конечно, поначалу это будет не так просто, постарайтесь дать детям возможность разобраться самостоятельно. Потом можно обсудить решение всем вместе или индивидуально. Можно ли сразу найти корневую вершину или вершину второго уровня? Хорошо, если дети смогут сами ответить на этот и подобные вопросы. 

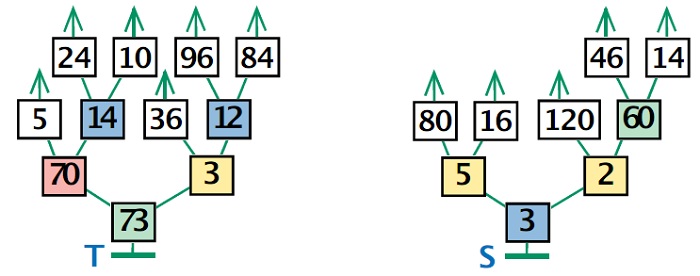
Заметим, что в вычислении значения выражения по дереву ошибиться в порядке действий гораздо сложнее, чем в примере. Действительно, ребенок просто не сможет по дереву начать с того действия, которое нужно делать позже, ведь в соответствующих вершинах пусто, а все те действия, которые можно выполнить сразу (в вершинах есть нужные числа), на самом деле допускают различный порядок выполнения. Так, например, в дереве Т можно сначала выполнить действия с числами 24 и 10, а затем 96 и 84, а можно поступить наоборот. В дереве S можно сначала выполнять действия с числами 46 и 14, а затем 80 и 16 либо наоборот. Если кто-то из ребят вас спросит, то обсуждать это лучше в индивидуальном порядке, в зависимости от уровня развития ребенка. С сильным ребенком можно обсудить общее правило порядка вычисления по дереву. Оно просто – сначала выполняются действия предпоследнего уровня (на последнем уровне всегда только листья и там ничего вычислять не нужно), затем предыдущего и т. д., пока мы не дойдем до корневой вершины. Причем если на одном уровне находится несколько действий, то порядок их выполнения может быть любым (порядок не влияет на результат). Для слабого ребенка при этом опора на правила порядка действий может оставаться единственной возможностью найти правильный ответ в примере, поэтому его не стоит запутывать. Если такой ребенок вас спросит, в какой последовательности надо выполнять действия на одном уровне, то можно сказать, что, как обычно, слева направо.

При выполнении подобных заданий ребята часто забывают перенести ответ из корневой вершины в окно в примере, на это нужно обратить внимание.

Ответ: 

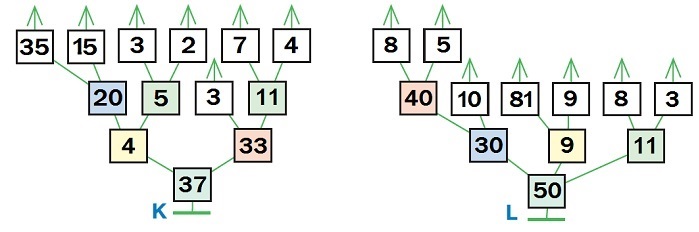
Задачи 94 и 95. Эти задачи сложнее задач 92 и 93, здесь надо заполнить не только цветные, но и белые окна дерева (листья), т. е. расставить числа, входящие в пример. Например, на предпоследнем уровне дерева К есть 2 зеленых окна, значит две следующие за каждым из них вершины должны участвовать в сложении. Но в примере два сложения в скобках. Чтобы разобраться, какие числа в какие белые окна нужно вписать, полезно посмотреть, что с результатами сложений будет происходить дальше, – обратить внимание на цвет окон второго уровня. Вы, наверное, увидите, что некоторые дети впишут числа в листья быстро, почти не задумываясь. Это не случайно, ведь мы стараемся выстраивать листья в дереве слева направо, так же как числа в записи примера.

После того как числа, встречающиеся в примере, правильно расставлены, задача становится аналогичной задачам 92 и 93. У дерева L есть одна особенность, которая еще нигде не встречалась и которую, возможно, заметят дети: одна из вершин дерева (корневая) имеет не две, а три следующих. Как известно, сложение обладает переместительным и сочетательным свойствами, в силу чего несколько чисел можно складывать в любом порядке и  даже одновременно. Поэтому, если в примере встречается сложение нескольких чисел подряд (без скобок между слагаемыми), мы будем рисовать в дереве три (или более) вершины, следующие за одной.

Ответ: 37 и 50.

Задача 96. Повторение операции склеивания мешков цепочек. В мешке-результате должно быть слово ПАРОВОЗ. Наиболее естественно предположить, что оно получается при склеивании цепочки ПАР из первого мешка, некоторой цепочки из второго мешка и цепочки ВОЗ из третьего мешка. Тогда во втором мешке должна лежать цепочка из одной буквы О. Поскольку в мешке-результате должно лежать 9 цепочек, а в одном из мешков-аргументов уже лежит 2 цепочки, значит, в третьем мешке должно быть 3 цепочки, в одном из оставшихся мешков – 3 цепочки, в другом – одна. Поскольку ни одна из цепочек: САМОЛЁТ и ТЕПЛОХОД не начинается на ПАР, скорее всего, в первом мешке должно лежать 3 цепочки, а во втором – одна (очевидно это и есть цепочка, состоящая из буквы О). Теперь ясно, что в первом мешке кроме цепочки ПАР должна лежать цепочка САМ, поскольку в слове САМОЛЁТ только одна буква О. Тогда в третьем мешке не хватает цепочки ЛЁТ. Третий и второй мешки достроены. Поскольку в третьем мешке лежит цепочка ХОД, а в мешке-результате должно лежать слово ТЕПЛОХОД, делаем вывод, что в первом мешке еще должна лежать цепочка ТЕПЛ. Теперь осталось выполнить склеивание мешков и убедиться, что в мешке-результате 9 цепочек и среди них есть 3 данных слова. 

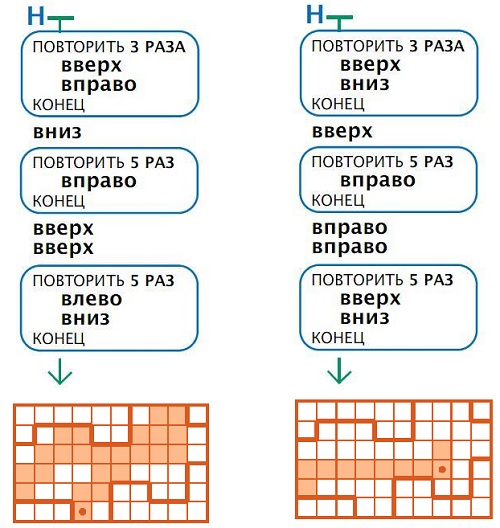
Задача 97. Ребенок будет действовать методом перебора: берем команду, получается – идем дальше, не получается – возвращаемся и берем другую. Несмотря на внешнюю сложность, программа составлена так, что ученику в любом случае не придется возвращаться больше, чем на шаг назад. Дайте ребятам побольше времени и они сами доберутся до ответа. Если ученик запутался, то начните рассуждать вместе с ним. Итак, какую команду вписать в первую конструкцию повторения? Сразу понятно, что не подойдут команды вверх и влево. Берем любую из оставшихся двух, например, вправо (на самом деле если взять команду вниз, то решение тоже можно достроить до конца). Выполняем первую конструкцию повторения. Робик оказывается в клетке, из которой невозможно движение ни вправо, ни вверх. Поставим в окно, например, команду влево и проанализируем следующую конструкцию повторения – не получается. Действительно, на данном поле ни из какой клетки не сделать 5 шагов ни вверх, ни вниз, а из той клетки, где очутился Робик, не сдвинуться на 5 шагов ни вправо, ни влево. Вывод – надо вернуться и поставить во второе пустое окно команду вниз, тогда в следующее пустое окно вполне можно написать – вправо. Аналогичные рассуждения можно продолжить, пусть ученик сделает это самостоятельно. Ниже приведены два варианта программы: первая – если вначале вписали команду вправо, вторая – если вначале вписали команду вниз, на самом деле их больше. Попробуйте найти хотя бы еще две возможные программы, тогда вам будет проще ориентироваться в решениях ребят.

 

Задача 98. Задача на повторение процедуры поиска выигрышной стратегии с опорой на раскрашенную числовую линейку. В игре камешки с ходами 1, 2 и 3 проигрышными являются все позиции, кратные четырем, поэтому для такой игры с начальной позицией 43 камешка выигрышной стратегией обладает Второй.

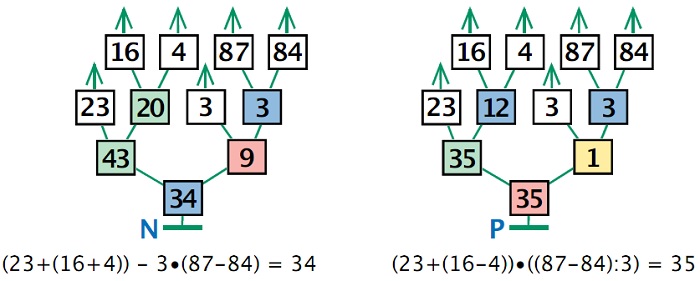
Задачи 99 и 100. Здесь ребятам необходимо не просто заполнить пустые окна дерева вычисления, но и написать выражение, для которого данное дерево было бы деревом его вычисления. Если при решении задач 92 – 95 ребята могли опираться на арифметические выражения, знакомые им из курса математики, то здесь полное и ясное понимание материала листа определения становится для решения задачи обязательным. Незаполненные деревья N и P отличаются только цветом окон. Значит, арифметические выражения будут составлены из одних и тех же чисел, но знаки между соответствующими числами будут различными.

В дереве N при сложении чисел 16, 4 и 23 задан определенный порядок (сначала складываются 16 и 4, затем к результату прибавляется 23), в то время как в задаче 95 три слагаемых складывались одновременно. Действительно, в данной теме будет встречаться и та и другая ситуация. В этой задаче, чтобы указать представленный в дереве порядок действий, лучше всего поставить скобки: 23+(16+4). Несколько хуже, если учащийся напишет 16+4+23, а например, вариант 23+4+16 в данном случае следует считать ошибочным, хотя на значение выражения порядок сложения не повлияет.

Работа с деревом Р – хороший повод повторить особенные случаи умножения и деления, ведь здесь встречается деление числа на себя и умножение на 1.

Ответ: 

Задача 101. Необязательная. Эта задача об установлении связи между древесной структурой и структурой арифметического выражения. В дереве порядок действий задается порядком уровней, т. е. сначала мы выполняем действия с числами, находящимися на предпоследнем уровне (если таких пар несколько, то установление порядка действий между ними несущественно), затем на втором с конца и т. д. В арифметическом выражении порядок действий устанавливается правилами очередности действий и скобками. В данной задаче ребятам необходимо расставить скобки так, чтобы порядок действий в примере стал таким же, как в дереве. Например, видно, что по дереву вычитание должно предшествовать умножению. Этого можно добиться, если в примере разность чисел 10 и 5 заключить в скобки. Впрочем, структура примера здесь не является особенно сложной, и мы надеемся, что ребятам не потребуется ваша помощь.

Ответ:

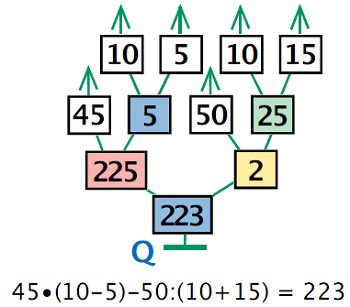
Задача 102. Необязательная. Задача аналогичная задаче 87. Технически эта задача проще, поскольку дерево здесь получится гораздо меньше. Поэтому данную задачу можно предлагать практически всем учащимся.

Задача 103. Многие дети догадаются начать решать задачу с самых простых требований к строящейся цепочке – первого и последнего. Когда будут построены фрагменты цепочки, отвечающие первому и последнему требованиям, достроить их до фрагментов, для которых выполнено второе условие, будет уже несложно, а сборка фрагментов в полную цепочку – дело уже совсем простое. Тем, кому трудно, можно посоветовать воспользоваться телесными объектами с листа вырезания, но от всех детей на данный момент этого требовать уже не стоит.

Задача 104. Необязательная. Стратегии в подобных задачах могут быть самые разные. Одна из них – по очереди брать слова и пытаться найти среди оставшихся два слова с таким же мешком букв. 

Компьютерный урок «Дерево вычисления», часть 1, задачи 84 – 90

Задача 84. Эта задача аналогична задачам 92 и 93 из учебника. От ребят требуется только заполнить цветные окна дерева – вычислить и впечатать значения арифметических действий.  

Ответ: 67.

Задача 85. Задача на построение дерева арифметического выражения. Подобных задач в курсе нет, поскольку на бумаге при решении такой задачи на ребенка ложится слишком много технической работы (рисование, раскрашивание и т. д.). Компьютерные возможности позволяют построить дерево вычисления относительно быстро, в результате ребенок может сосредоточиться на содержании задачи.

Лучше сначала спланировать общую структуру дерева. Так, в нашем примере есть три ступени действий, которые необходимо делать друг за другом. Первыми нужно выполнить действия в скобках, затем нужно выполнить умножение и в конце - сложение. Таким образом, числа, стоящие в скобках, будут находиться в листьях, результаты действий в скобках – в окнах предыдущего уровня, результат умножения – на один уровень раньше и результат сложения (значение выражения) – на первом уровне. Рассуждая так, получим, что наше дерево будет иметь 4 уровня: на первом уровне одна вершина, на втором – две, на третьем – две, на четвертом – четыре. После того как мы определились с общей структурой дерева, можно строить дерево (с помощью инструмента дерево), выбирая из библиотеки прямоугольники, соответствующие цветам действий, и нужные числа.

Ответ:

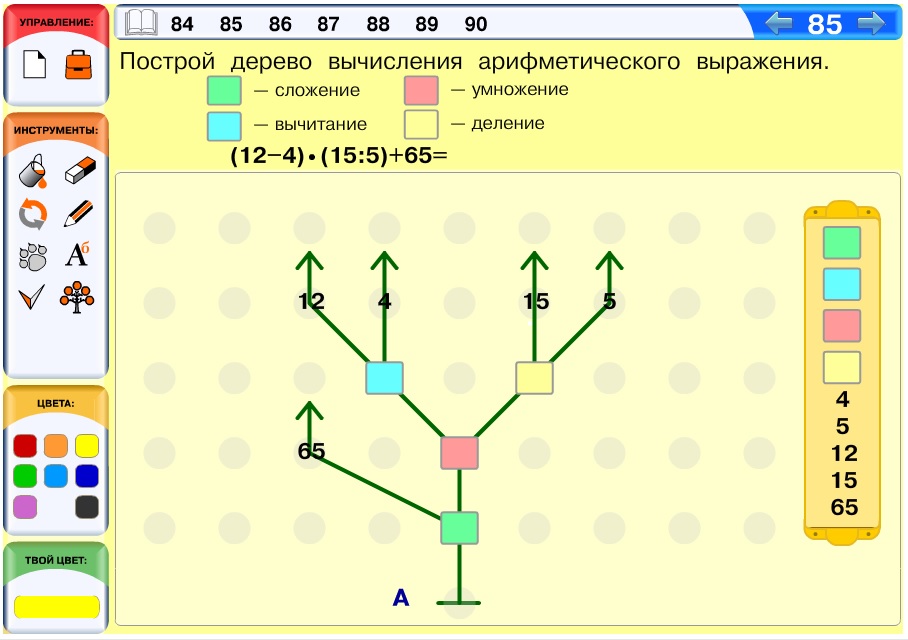
Задача 86. Задача, аналогичная компьютерной задаче 84.

Ответ: 486.

Задача 87. Построение дерева игры ползунок.

Один из вариантов ответа:

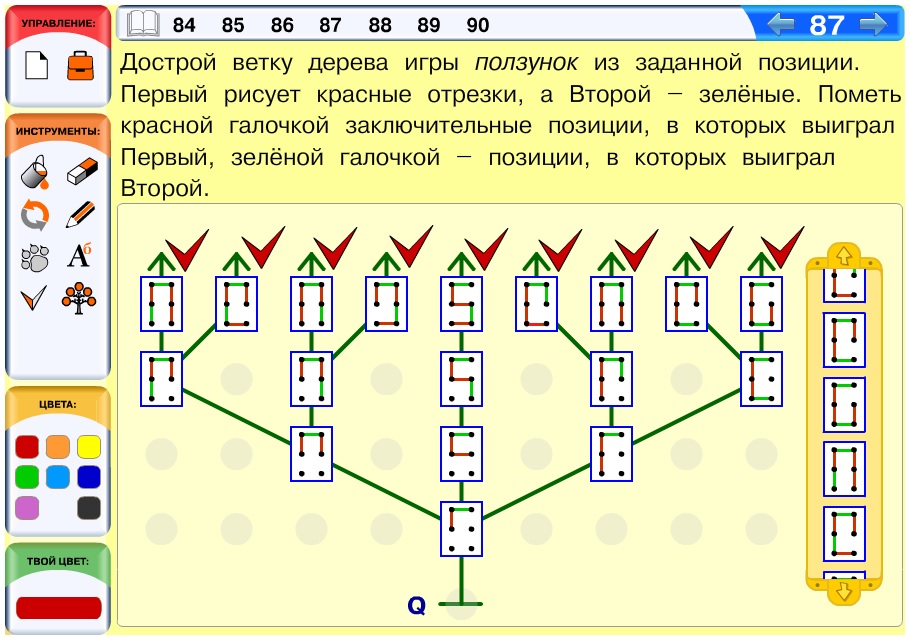
Задача 88. Вариант ответа:

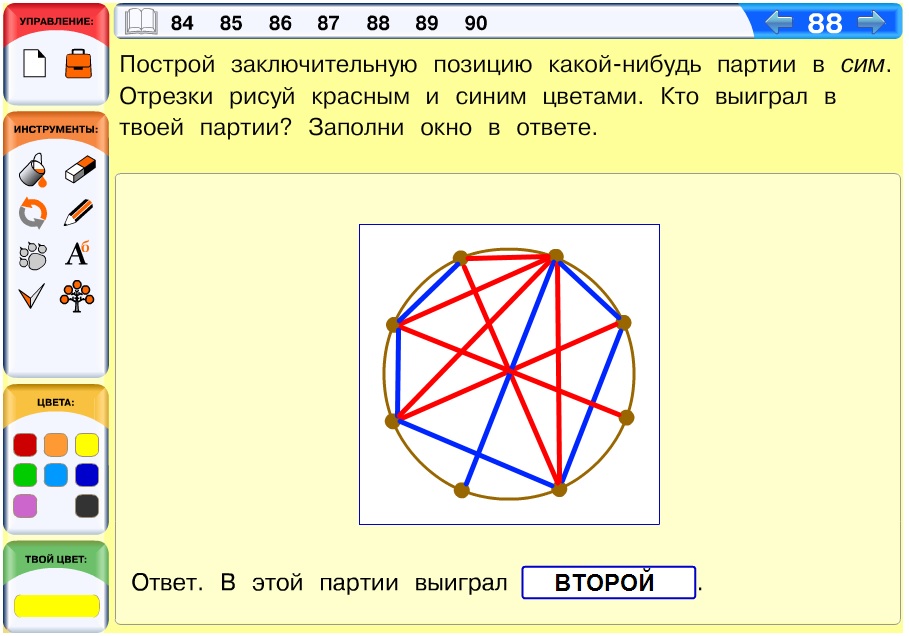
Задача 89. Раскрашиваем числовую линейку:

На первый вопрос задачи теперь ответить несложно – судя по последовательности раскрашенных клеток, клетка 24 будет красной, значит, выигрышную стратегию в игре с такими правилами и начальной позицией 24 камешка будет иметь Первый. Для ответа на второй вопрос ребята, вероятно, будут продолжать раскрашивать числовую линейку до позиции 27. Однако, можно заметить закономерность в чередовании выигрышных и проигрышных позиций: позиции 23, 24, 25 и 26 будет красными, а 27 – синей. Значит, в игре с начальной позиций 27 выигрышной стратегией обладает Второй. 

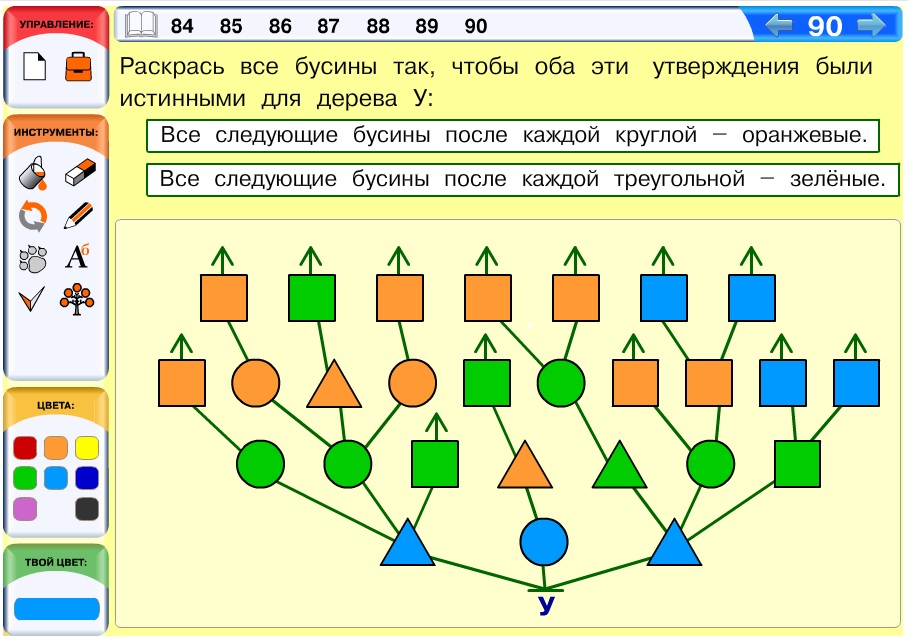
Задача 90. Задача на повторение конструкции после каждой и применение ее для бусин дерева. После того как будут раскрашены в нужный цвет все бусины, следующие после круглых, и все, следующие после треугольных, в дереве останется 7 нераскрашенных бусин – 4 следующих за квадратными и 3 корневых. Их нужно обязательно раскрасить, но выбор цвета здесь не ограничен – можно использовать и оранжевый с зеленым.

Вариант ответа:

Компьютерный урок «Дерево вычисления», часть 2, задачи 91 – 97

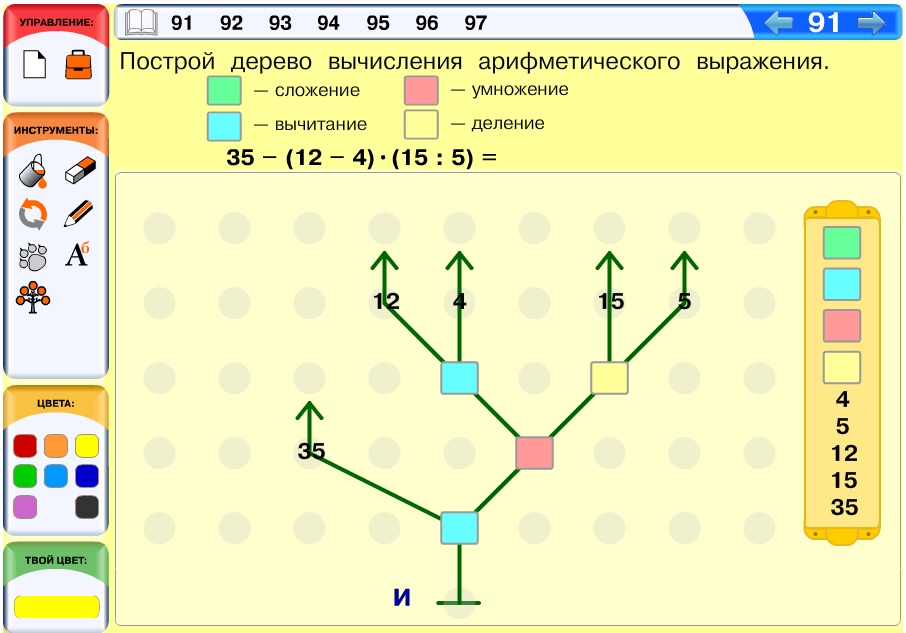
Задача 91. Продолжаем работать с деревьями вычисления (см. комментарии к задаче 85 этого курса).

Вариант ответа:

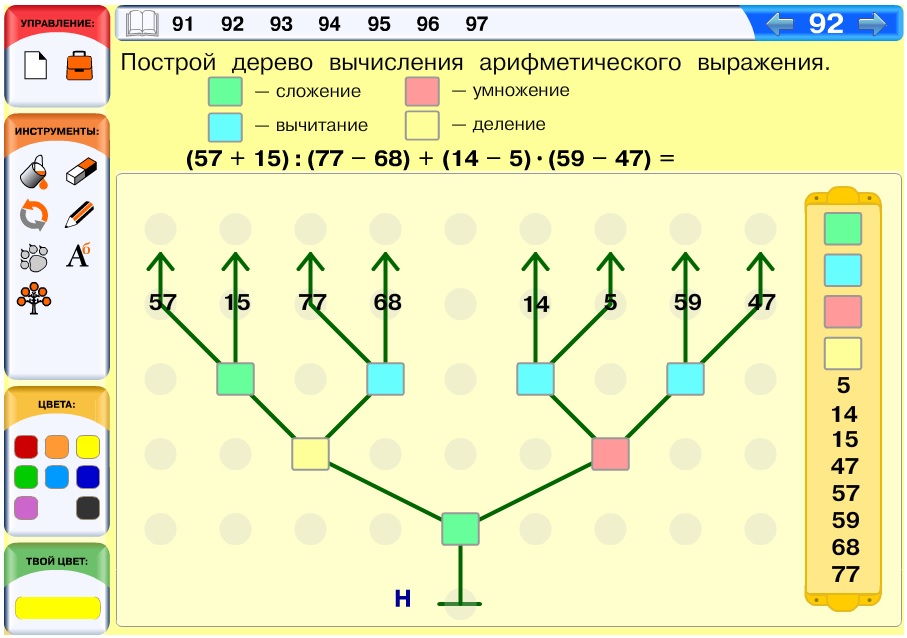
Задача 92. Эта задача аналогична предыдущей. Отличие – более сложное арифметическое выражение, соответственно и дерево будет иметь более сложную структуру.

Вариант ответа:

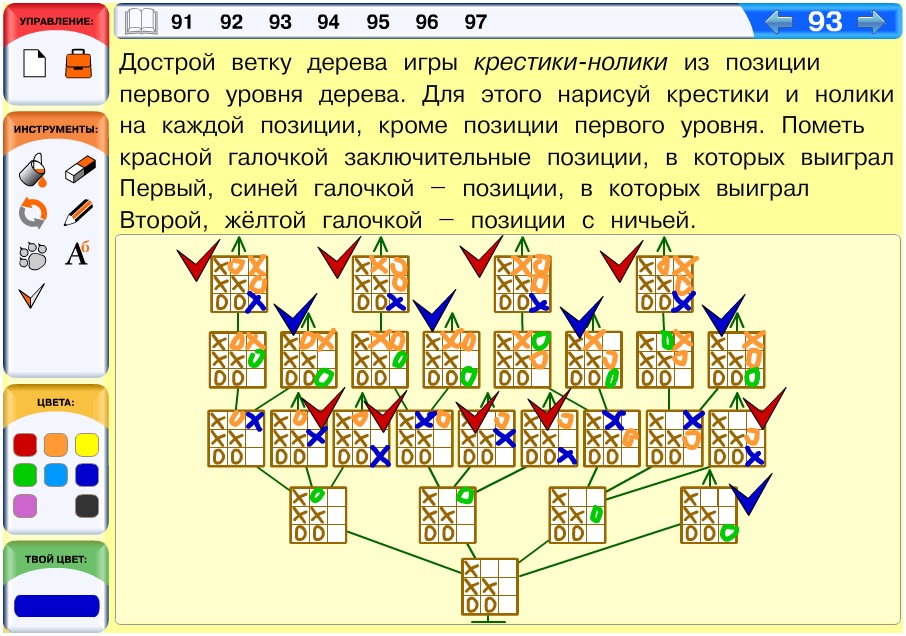
Задача 93. Эта задача технически отличается от других компьютерных задач о построении дерева игры крестики-нолики тем, что вместо выбора нужных полей из библиотеки здесь требуется дорисовать крестики и нолики на позициях в уже построенном дереве. Так как структура дерева задана, то в начале решения нужно провести небольшой анализ.

В позиции первого уровня ноликов меньше, чем крестиков, значит, очередь сделать ход – за ноликами. В данной задаче важно правильно определить, в какой клетке каждой из четырёх позиций второго уровня нужно поставить нолик.

На втором уровне в первой правой ветке стоит всего одна позиция-лист: эта позиция должна быть заключительной. Рисуем нолик в нижнем правом углу поля – и получаем, что Второй выигрывает. Структура двух веток слева одинакова – на третьем уровне есть два листа, т. е. первый нолик (на втором уровне) надо поставить так, чтобы на третьем уровне у Первого было две выигрышные позиции. Поэтому ставим нолики в двух верхних правых клетках. Соответственно на третьем уровне второй правой ветки ставим нолик в среднюю клетку правого ряда. Дальше решение строится стандартно.

Вариант ответа:

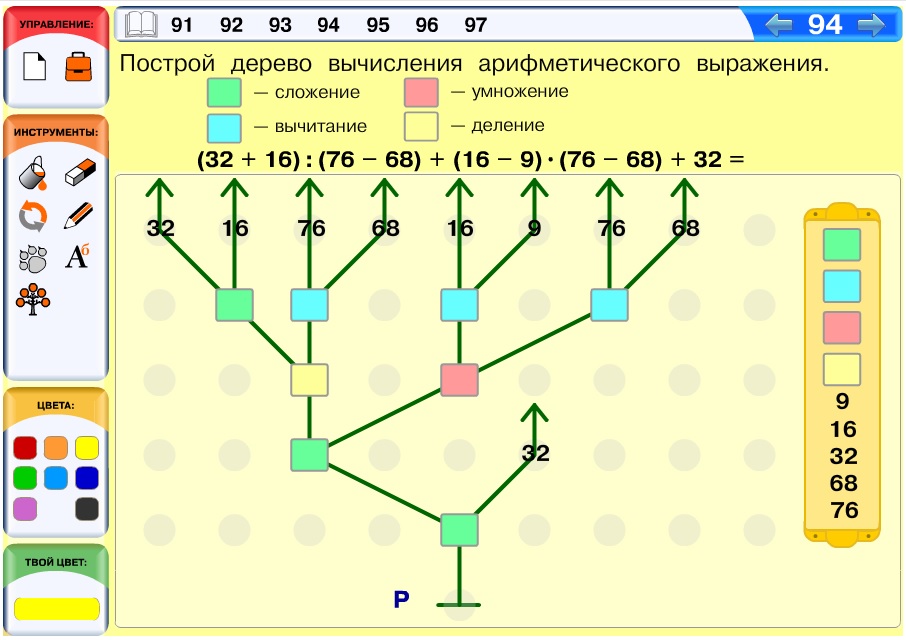
Задача 94. Задача, аналогичная задачам 91, 92. 

Вариант ответа:

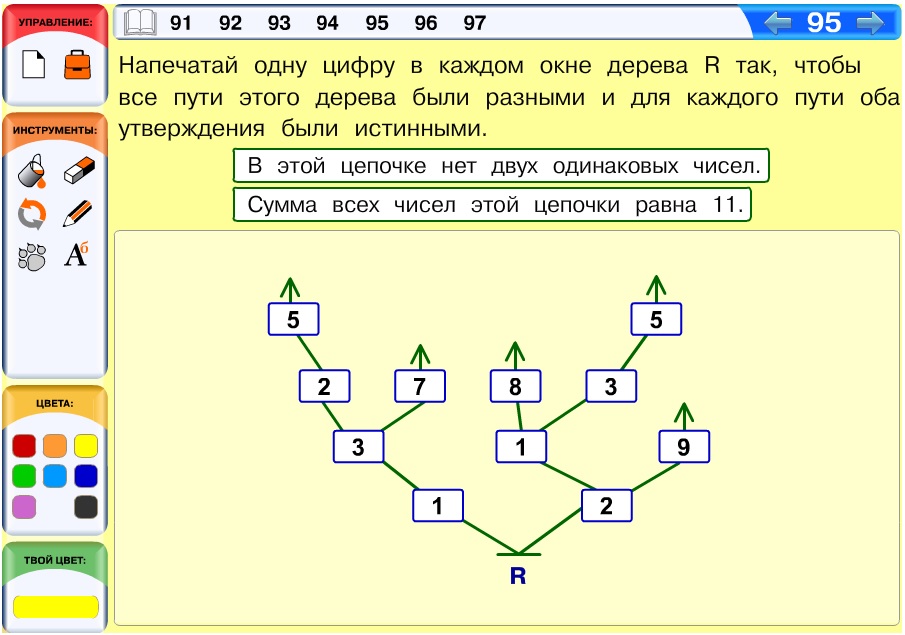
Задача 95. Усложненная задача, выходящая в курс математики. Многие дети, как всегда, будут пытаться построить решение методом проб и ошибок, но проб может потребоваться достаточно много. В выигрыше окажутся те дети, которые проведут некоторые предварительные рассуждения. Самое сложное – построить два самых длинных пути. Нужно представить число 11 в виде суммы четырех различных слагаемых. Если не использовать нуль, то получится ровно один вариант: 11 = 1 + 2 + 3 + 5. Если 0 использовать, то добавится еще много вариантов.

Разберем здесь только один вариант: 11 = 1 + 2 + 3 + 5. В бусинах первого уровня можно пробовать ставить два разных числа из набора: 1, 2, 3, 5. Например, поставим 1 и 2. Заметим, что в правой ветке нельзя поставить 1 (подумайте, почему). Поставим в правой ветке 2, а в левой 1. Дальше решение оказывается достроить несложно. Оно не единственное в этой задаче, но решений здесь немного и случайно наткнуться на него непросто.

Вариант ответа:

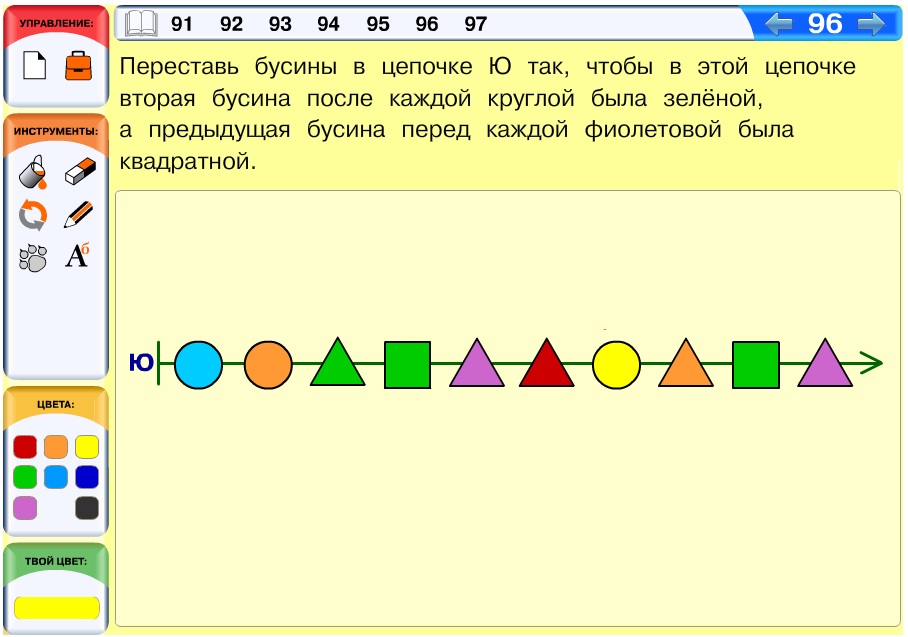
Задача 96. Задача повышенного уровня сложности, в которой повторяются понятия перед каждой/после каждой. Основная трудность здесь в том, что решение не удается составить из частичных решений вида «круглая – … – зеленая» и «квадратная фиолетовая» – здесь частичные решения приходится «сращивать» между собой.

Вариант ответа:

Задача 97. Если в курсах 2–3 классов вы не пропустили проект «Римские цифры», эту задачу можно предложить всем ребятам.