Информатика. 4 класс Демо+методичка

Уроки 4 – 5. «Игра камешки»

Игра камешки хороша тем, что в ней не так трудно провести полный анализ игры и понять, кто когда выигрывает. Эта игра является основой при изучении темы «Выигрышные стратегии». На данном листе определений дети пока просто знакомятся с формальными правилами данной игры.

Решение задач из учебника

Задача 11. Задача на понимание правил игры камешки. Посоветуйте ребятам помечать позиции, получающиеся после хода Первого, синим цветом, как это сделано на листе определений. При осознанном решении ребята должны отвечать на вопросы, кто из игроков сделал ход из той или иной позиции и кто выиграл в данной партии.

Задача 12. В процессе решения данной задачи все учащиеся должны освоить правила игры камешки. Для начала можно провести одну – две партии на доске и попросить ребят написать цепочки для проведенных партий. Заполнять таблицу, как и во всех задачах на проведение турниров в малых группах, лучше всего по ходу игры, т. е. заносить в нее результаты по окончании каждой партии. В пустых клетках заголовка таблицы нужно написать имена или фамилии игроков, но не номера, иначе дети будут путать их с Первым и Вторым. Как видите, в условии задачи определена очередность хода игроков, которая позволяет членам каждой пары одинаковое число раз побыть на месте Первого и на месте Второго. На самом деле Первый в этой игре обладает выигрышной стратегией, это ребятам еще предстоит узнать в дальнейшем. Возможно, кто-то из сильных учащихся в ходе игры и особенно ответов на вопросы обратит внимание на то, что Первый выигрывает чаще Второго. Такому ученику можно дать задание подумать, почему так получается и как именно должен играть Первый, чтобы выиграть наверняка (как бы ни играл Второй).

Задача 13. В отличие от задачи 11, здесь нужно написать не просто цепочку партии, а цепочку, удовлетворяющую определенному условию (выигрышу конкретного игрока). Эту задачу можно решать достаточно формально – сначала написать на листочке любую цепочку партии с разрешенными ходами и заданной начальной позицией. Далее нужно определить победителя в этой партии, а чтобы ребятам сделать это было проще, посоветуйте им помечать результаты ходов Первого своим цветом, как это сделано на листе определений. Если кто-то из ребят нарисовал все бусины цепочки одним цветом, то попросите его расставить над каждой бусиной, начиная со второй цифры, римские I или II в зависимости от того, кто из игроков привел игру к этой позиции. Итак, мы нарисовали произвольную цепочку игры, например:

Оказалось, что в данной партии выиграл Второй, значит, эту цепочку следует записать во второе окно. Чтобы получить теперь цепочку, в которой бы выиграл Первый, достаточно немного поправить уже составленную цепочку, сделав в ней на одну бусину больше или на одну бусину меньше. Оказывается, это можно сделать всегда. Действительно, в процессе игры кто-то из игроков сделает хотя бы один ход в 2 или 3 камешка либо все ходы будут по одному камешку. В первом случае мы сможем разделить ход на два (1 и 1 или 1 и 2), во втором – мы сможем сделать из двух ходов по одному камешку один ход. Например, нашу цепочку можно переделать так:

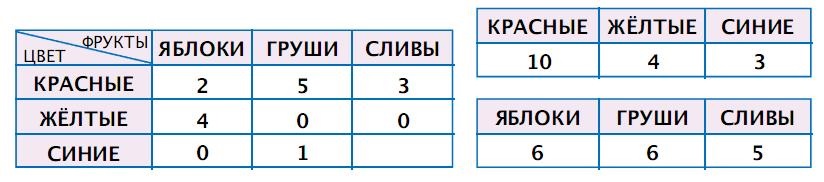
Задача 14. Данная задача на установление соотношений между одномерными и двумерной таблицами для одного мешка. Во 2 части курса («Информатике 3 – 4») ребятам уже приходилось встречаться с задачами, где требовалось заполнить для одного мешка и одномерные, и двумерную таблицы. Тогда мы советовали вам обратить внимание ребят на совпадение сумм по столбцам (или по строкам) двумерной таблицы с соответствующими числами одномерной таблицы и использовать полученную закономерность в ходе проверки. Впрочем, тогда без этого можно было обойтись. Здесь же для решения необходимо понимание характера связи чисел в разных таблицах. Например, учащиеся должны понимать, что общее число красных фруктов в двумерной таблице (сумма чисел второй строки) равняется числу в первом столбце первой одномерной таблицы (10). Исходя из этого, можно заполнить пустую клетку во второй строке двумерной таблицы. Аналогично можно заполнить пустую клетку в последнем столбце двумерной таблицы, используя число слив, содержащееся во второй одномерной таблице. Так продолжаем рассуждать до тех пор, пока вся двумерная таблица не будет заполнена. После этого можно будет заполнить пустую клетку в одномерной таблице.

Ответ:

Задача 15. Здесь можно играть за двоих, подыгрывая либо Первому, либо Второму. Однако можно попытаться объяснить ребятам и «честное» решение, в котором никто никому из игроков не подыгрывает. Проанализируем ситуацию, создавшуюся на поле. Учитывая очередность ходов, можно сделать вывод о более выгодном положении Второго игрока (его очередь делать ход). Среди всех возможных его ходов самый выгодный – поставить нолик в правый верхний угол.

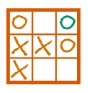
Этим Второй одновременно мешает Первому получить три крестика на диагонали и создает позицию, приводящую к собственной победе вне зависимости от следующего хода Первого. Действительно в сложившейся позиции Второй может получить три нолика либо на верхней горизонтали, либо на правой вертикали, а Первый при этом следующим ходом может помешать ему получить только одну из этих троек. Итак, если Второй играет «по-настоящему», то он наверняка сделает этот выигрышный ход, и мы достроим цепочку В (ведь именно партия с цепочкой В должна закончится выигрышем Второго!), например, так:

Теперь надо все-таки построить цепочку А игры, где выигрывает Первый. Для этого Второму придется «подыграть» Первому, не делать своего выигрышного хода и поставить нолик не в правую верхнюю клетку. Тогда партия сразу закончится выигрышем Первого, и мы достроим цепочку А, например, так:

Задача 16. Необязательная. Эта задача совсем простая, но она дает ребятам представление о том, что в некоторых партиях игры камешки у игрока просто нет выбора. Иногда это касается только одного игрока, т. е. он проигрывает при любых своих ходах. Гораздо реже такая ситуация касается обоих игроков, и партия предопределена с самого начала, как в данной задаче. Чтобы все учащиеся заметили это, в задаче приведено последнее задание, в котором ребята должны подумать, существует ли хотя бы одна другая цепочка партии по тем же правилам (конечно, такой цепочки не существует).

Задача 17. В задаче надо сопоставить множество возможных инструкций с результатом выполнения инструкции (раскрашенной цепочкой). Первое, что приходит в голову, – пытаться последовательно брать все инструкции и их применять. Сильные дети наверняка будут ставить лишь пометки, соответствующие цвету, под бусинами исходной цепочки. Слабым детям облегчите задачу, выдав нераскрашенные цепочки. Тогда ребята смогут просто раскрашивать эти цепочки по инструкциям, а затем результат сопоставлять с данной цепочкой. Обратите внимание, что данная цепочка могла получиться в результате выполнения разных инструкций. И вы, и ребята, скорее всего, сталкивались с тем, что в жизни совершенно разные действия приводят к одному и тому же результату. В условии задачи мы это подчеркиваем словом «могла». Однако из приведенных инструкций подходит только одна – третья.

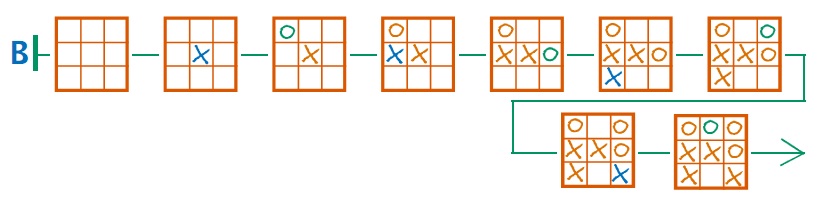
Задача 18. Задача на повторение темы «Все пути дерева», которая имеет несколько дополнительных сложностей. Во-первых, слова-пути включают внутрисловные знаки, следовательно, ребятам необходимо вспомнить, что дефис и апостроф – отдельные символы, требующие помещения в отдельные вершины. Во-вторых, дерево Q должно иметь определенное число вершин (23), а общее число знаков в словах мешка гораздо больше, значит, при построении дерева нужно экономить вершины. Например, все слова в мешке начинаются либо с буквы К, либо с буквы О, значит, в дереве Q можно поставить только две корневые вершины, а не 7 по числу слов в мешке. Теперь рассмотрим слова, начинающиеся с буквы К. Во всех этих словах следующая после буквы К – буква О, значит, в дереве у вершины К будет одна следующая вершина. В словах, начинающихся с О, встречаются две вторые бусины – буква Н и апостроф, значит, в дереве у корневой буквы О будет две следующие вершины. Так нужно стараться уменьшать число вершин в дереве, где это возможно. В конце, конечно, нужно проверить, что в дереве Q действительно 23 вершины.

Ответ:

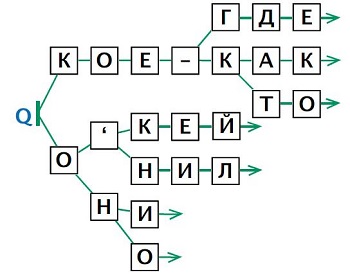
Задача 19. Обратите внимание, на поле Робика есть стены. Лабиринт очень полезен для освоения конструкций построения программ, где используются условия (в частности, конструкция «ЕСЛИ-ТО-ИНАЧЕ»), с которыми дети встретятся на уроках информатики в средней школе.

В ходе написания программы Р от ребят потребуется понимание того, как стенки ограничивают перемещения Робика. Например, Робик сломается, если из начального положения мы заставим его выполнить команду вправо или вверх, так как он не может проходить через стены. Первая команда по условию – вниз. Вторая команда опять не может быть вправо, зато подойдут все три оставшиеся команды. Аналогичным образом нужно и дальше учитывать положение стенок и границ поля при написании программы Р.

Вот позиция Робика после выполнения программы М:

Задача 20. Как и задача 10, данная задача на повторение темы «Склеивание цепочек», но здесь ребятам необходимо для решения вспомнить некоторые сведения из курса русского языка. Если вы опасаетесь, что ребята забыли, что такое основа слова, предварительно повторите данный материал на уроке русского языка.

Задача 21. Задача на повторение правил проведения кубкового турнира, которые дети повторяли в рамках проекта «Турниры и соревнования», 1–2 часть. Для решения этой задачи нужно хорошо понимать закономерности игры камешки и правила построения цепочек партий этой игры. Так по длине каждой партии нетрудно понять, какая пара ее провела. Например, в первой партии выиграл Первый (Оля), значит число ходов в ней нечетное. Значит, длина партии Оли и Лена три или пять ходов. Исходя из тех же соображений, длина партии Яна и Коли 4 хода. Значит длина последней партии турнира нечетная – выиграл Первый (Оля). Теперь в каждом из окон осталось написать цепочки партий заданной длины. Обратите внимание, длина партии и длина цепочки партии – разные числа. В цепочке партии бусин всегда на одну больше, чем в партии ходов.

Задача 22. Необязательная. При заполнении каждого окна возможны разные варианты. Тем не менее кто-то из учеников может затрудниться с решением этой задачи, поскольку все слова начинаются на «ША», а таких в русском языке сравнительно немного. Там, где между третьими буквами уже данных соседних слов, стоит несколько букв, слово найти проще. В некоторых данных соседних словах и третьи буквы одинаковы, в таких случаях искать слова сложнее. Где-то помогает правило словарного порядка для случая, когда одно слово является частью другого. Например, между словами ШАБЛОН и ШАГОМ можно поставить слово ШАГ, а между ШАЛУНЬЯ и ШАЛИТЬ – слово ШАЛИТ. Если нужного слова ребенку найти никак не удается, можно разрешить ему поискать слово в словаре.

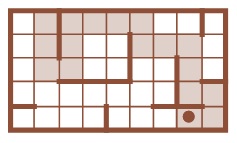
Задача 23. Необязательная. Во 2 части курса ребята уже встречались с подобными задачами. Их можно решать методом проб и ошибок или методом перебора, поочередно запуская Робика из каждой закрашенной клетки. Здесь поможет анализ программы и некоторые рассуждения, которые позволят уменьшить этот перебор. Так можно сразу отбросить все клетки, из которых нельзя выполнить первую команду влево (таких оказывается три), а затем из оставшихся исключить клетки, из которых нельзя выполнить первые две команды (таких оказывается еще две). Остальные пять закрашенных клеток можно проверить более внимательно. Другой вариант (для сильных учеников) – анализировать программу с конца. Так, клеток, из которых можно выполнить команду вправо 3 раза, среди закрашенных всего две, значит после выполнения первых 6 команд программы Робик может находиться в одной из них. А поскольку четвертая с конца команда – вверх, можно безошибочно указать единственную закрашенную клетку, в которой будет находиться Робик после выполнения первых 5 команд программы (первая клетка во второй закрашенной строке). Теперь осталось выполнить первые 5 команд программы в обратном порядке.

Ответ:

Задача 24. Необязательная. При решении задачи ребята могут столкнуться с двумя трудностями. Во-первых, в задании фигурируют два вида мешков: мешки мешков («внешние» мешки) и мешки бусин («внутренние» мешки), которые названы одним и тем же словом – мешок; кто-то может запутаться, где какой мешок имеется в виду. Можно прямо в условии сделать пометки – «внешний» и «внутренний» или «большой» и «маленький». Тогда условие приобретает вид: «Найди один мешок мешков (большой), в каждом мешке (маленьком) которого есть две одинаковые бусины».

Во-вторых, сложной может оказаться логическая структура высказывания, поскольку содержит два квантора: для каждого и есть. Если кому-то трудно сразу понять структуру текста задания, порассуждайте вместе. Нужно разобраться со всеми мешками: где есть две одинаковые бусины, а где их нет. Можно те мешки, где есть пара одинаковых бусин, как-то пометить (надо проследить, чтобы пометки отличались от галочек, которые нужно поставить в соответствии с заданием). Чтобы довести рассуждения до конца, спросите: «В большом мешке сколько должно быть мешков с двумя одинаковыми бусинами?» Читая условие, ребята обязательно обратят внимание на слово каждый. Это означает, что каждый из трех (или четырех) внутренних мешков должен содержать две одинаковые бусины. Теперь посмотрим, в каком «большом» мешке все «маленькие» мешки оказались помечены. Искомый мешок В.

Компьютерный урок «Игра камешки, часть 1», задачи 15 – 21

Задача 15. Данная задача аналогична задачам учебника о построении цепочки игры. Однако использование компьютера позволяет ребёнку легко создавать цепочки партий игры, не тратя на это много времени. В такой цепочке каждая позиция выглядит как кучка камешков, а не просто число – так нагляднее. Дети будут, скорее всего, строить партию методом проб и ошибок. Однако здесь удобно воспользоваться и полным перебором.

Итак, нам нужна партия, в которой было сделано ровно 5 ходов. Для этого (переводя задачу в математическую плоскость) нам необходимо представить число 11 в виде 5 слагаемых, каждое из которых может быть равно 1, 3 или 4. Перебор удобно вести начиная с наибольших слагаемых. Сколько в партии с такими правилами может быть сделано ходов по 4 камешка? Два, один или ноль. Допустим, таких ходов сделано два. Тогда число 11 представляется в виде пяти слагаемых так: 4+4+1+1+1. Теперь предположим, что в партии был сделан один ход в 4 камешка. Тогда ходов по 3 камешка могло быть два, один или ноль. Разберём каждый из этих случаев. Видим, что ни в одном из них решение не выстраивается.

Теперь допустим, что ходов в 4 камешка в партии сделано не было. Тогда ходов в 3 камешка могло быть сделано три, два, один, или ноль. Рассмотрим каждый из этих случаев. В одном из них выстраивается решение: 3+3+3+1+1. Таким образом, данная задача имеет ровно 2 решения. А учитывая, что сделано нечётное число ходов (при этом в цепочке игры чётное число позиций), в этой партии выиграл Первый.

Задача 16. Здесь проще всего использовать метод проб и ошибок. Для начала построим любую партию игры. Если в ней выиграл Первый, значит решение мы уже нашли. Если выиграл Второй, то партию всегда удастся перестроить так, чтобы она соответствовала условию: например, в такой партии всегда найдётся ход 4 камешка, который можно разделить на 3 и 1, либо ходы 3 и 1, которые можно объединить в один, либо 4 хода по 1 камешку, которые можно объединить в один.

Задача 17. Здесь, как и при решении предыдущей задачи, стоит просто начать играть – построить цепочку какой-нибудь партии. И затем постараться подредактировать полученную цепочку – удлинить ее, разделив какой-то ход в 4 камешка на два хода по 2 камешка. Или укоротить – объединить два хода по 2 камешка в один ход с 4 камешками.

Задача 18. Повторение лексики, связанной с цепочками, в частности понятий «перед каждой/после каждой» и «раньше/позже». Наибольшую сложность здесь представляет соблюдение третьего условия, кто-то из ребят может запутаться. Посоветуйте такому ребёнку начать с жёлтых треугольных бусин. В частности, спросите, какая бусина должна стоять перед первой по счёту жёлтой треугольной бусиной в цепочке. Ясно, что это жёлтая круглая бусина. Тогда какая бусина должна стоять перед второй по счёту жёлтой треугольной бусиной? Так постепенно в ходе последовательности вопросов выясняется, что в нашей цепочке обязательно должен быть кусочек «жёлтая круглая – жёлтая треугольная – жёлтая треугольная – красная треугольная». Положение остальных бусин в цепочке определяется не столь жёстко.

Задача 19. Знакомая детям задача на повторение темы «Мешок бусин цепочки» - игра в анаграммы.

Ответ (по одному из возможных вариантов): БОЧКА, СТАРИК, РУЧКА, ЛОДКА.

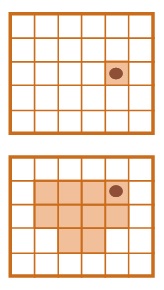
Задача 20. Повторение конструкции повторения. Конечно, для поиска решения здесь можно было бы провести полный перебор клеток поля, но это долго. Лучше этот перебор сократить, проанализировав заданную программу. В процессе выполнения программы Робик должен передвинуться на 6 клеток вверх, значит в начальной позиции он должен стоять в одном из трёх нижних рядов поля. Клетки трёх правых крайних столбцов этих рядов не подходят, потому что из этих клеток не удастся выполнить 3 команды «вправо». Таким образом, для перебора остается 15 клеток. Из семи из них нельзя выполнить две команды «вверх», поэтому мы их тоже отбрасываем. В результате у нас остается только 5 подходящих клеток, которые можно перебрать, «запустив» из них Робика, и найти единственное решение.

Задача 21. Предложите эту несложную задачу детям, у которых осталось время на уроке. Сильным учащимся лучше предложить одну из необязательных задач из учебника.

Компьютерный урок «Игра камешки, часть 2», задачи 22 – 28

Задача 22. По виду эта задача напоминает компьютерную задачу 16, однако по содержанию она ближе к задаче 15. Если перевести решение в математическую плоскость, то чтобы построить искомую партию, достаточно представить число 12 в виде четырёх слагаемых, каждое из которых равно 1, 2 или 3. В данном случае задача имеет одно решение – в искомой партии должно быть сделано 4 хода по 3 камешка. Отметим, что на вопрос задачи можно ответить ещё до построения цепочки, так как четвёртый ход в игре делает Второй.

Задача 23. Не слишком сложная задача на игру в камешки, но новая по формулировке. Здесь некоторые позиции партии построены, а остальные – нужно достроить самим ребятам. Ясно, что в цепочке, кроме двух заданных позиций в 9 и 2 камешка, определены ещё начальная (14 камешков) и заключительная (0 камешков) позиции. Поэтому, в сущности, ребятам необходимо достроить ровно 3 позиции. Все они определяются разницей в числе камешков двух соседних построенных позиций. Так в начальной позиции 14 камешков, а в третьей позиции – 9 камешков. Между этими позициями было сделано 2 хода и взято 5 камешков. Исходя из правил игры, это могли быть только ходы в 4 и 1 камешков (в любом порядке). Аналогично определяем, что между третьей и пятой позицией были сделаны ходы 3 и 4 камешка, а на предпоследнем и последнем ходу было взято по 1 камешку.

Задача 24. Повторение терминологии, относящейся к цепочкам – «после каждой». Для решения этой задачи важно внимательно отнестись к условию. Собственно вся сложность решения заключается именно в сложности формулировки, а сама задача – несложная. В цепочке Ф 5 птиц и 4 лягушки. Выполняя первое условие, расставляем фигурки через одну: птица – лягушка – птица – лягушка – … – птица. Теперь проверяем выполнение второго условия – оно оказывается выполненным.

Задача 25. Несложная задача на повторение правил игры крестики-нолики. Если кто-то из ребят допустил ошибку, стоит попросить его вернуться к тому месту листа определений «Игра крестики-нолики», где описываются возможные заключительные позиции в игре крестики-нолики.

Задача 26. Похожие задачи, но без конструкции повторения, ребята уже решали. Поэтому, надеемся, все ребята будут знать, с чего начать решение. Дети, скорее всего, будут перебирать все клетки поля, выбирая наугад. Но может быть, кто-то из детей будет готов сначала проанализировать ситуацию. При анализе программы становится ясно, что после выполнения конструкции повторения Робик должен оказаться во второй клетке справа второго ряда снизу. А при анализе конструкции повторения будет понятно, что выполнение команд конструкции «вправо―вправо―вниз―влево» равнозначно выполнению команд «вправо―вниз». Рассуждая таким образом, достаточно легко найти количество повторений конструкции ― их будет 4.

Задача 27. Задача на построение цепочки игры в слова. Если кто-то из детей не знает правил этой игры, обсудите их вместе в классе. Обратите внимание, что не все слова будут участвовать в нашей цепочке: слов 12, а окон цепочке 9, два слова останутся. Это может запутать кого-то из детей – обратите внимание такого ребенка, что в условии не сказано, что надо положить ВСЕ слова в окна. Два лишних слова будут давать тупиковые решения, тем самым делая поиск решения не слишком простым. Например, рассмотрим слово КУКУРУЗА. Слов с последней «К» среди данных нет, значит это слово либо первое, либо не участвует в построении цепочки. Поставим его в цепочку первым. Тогда дальше цепочка строится однозначно КУКУРУЗА – АСПИРИН – НАБАТ – ТРИКОТАЖ – ЖЕРЕБЕЦ – ЦЕЛЬ – ЛУКОШКО. Слов с первой «О» у нас нет, значит дальше цепочка не достраивается, а она должна быть длины 9. Таким образом, мы пришли к выводу, что слово КУКУРУЗА в цепочке не участвует. Попутно мы понимаем, что слово ЛУКОШКО или последнее в цепочке, или тоже в построении цепочки не участвует. Значит, можно попробовать построить цепочку с конца. Здесь нам сразу же везёт, и мы получаем решение: ПОКОС – СИРОП – ПОЗЁМКА – АСПИРИН – НАБАТ – ТРИКОТАЖ – ЖЕРЕБЕЦ – ЦЕЛЬ – ЛУКОШКО.

Задача 28. Задача на повторение алгоритма подсчета областей картинки. Областей в этой картинке довольно много, однако большинство из них легко выделяются, да и компьютерная заливка оказывает при решении существенную помощь.