Информатика. 4 класс Демо+методичка

Урок 3. «Правила игры. Цепочка позиций»

Правила игры

Оказывается, все игры, которыми предстоит заниматься детям, имеют много общего. У всех таких игр есть правила, которые определяют начальную позицию, ход игры, мешок всех возможных позиций, заключительную позицию и наконец, победителя игры (или ничью). На этом листе определений правила игры крестики-нолики сформулированы с использованием новых терминов. Это поможет ребятам быстрее усвоить понятия со с. 8. Поэтому лучше предложить ребятам изучить листы определений на страницах 8 и 9 не по отдельности, а один за другим и только после этого отвечать на вопросы детей.

Цепочка позиций

С введением понятия позиция игры у нас появляется возможность ввести понятие цепочка позиций (партии игры), которое дает ключ к более глубокому, содержательному анализу каждой партии. Понятия позиция игры и цепочка позиций позволят нам существенно расширить круг задач и таким образом подвести детей к выводу общих закономерностей в играх с полной информацией.

Решение задач из учебника

Задача 6 ― на понимание новых листов определений. Решений у этой задачи, конечно, много. Для некоторых детей может показаться непривычным, что им нужно играть одновременно за двоих, сложно будет стремиться к выигрышу и того и другого. Но этого здесь и не требуется. Тем, кто быстро решит задачу, можно предложить ее усложнение: как может выглядеть цепочка позиций партии, закончившийся выигрышем Первого, Второго, вничью (подобные задачи появятся в учебнике позднее).

Попросите детей отмечать вновь появляющийся крестик синим цветом, а нолик – зеленым, как это сделано в начальной части цепочки. Это заставит детей более тщательно переходить к каждой следующей позиции игры и делать меньше ошибок. Кроме того, это позволит детям лучше понять, какой из игроков делает ход в каждой позиции, а значит, поможет им избежать ошибок в дальнейших, более сложных задачах.

На вкладыше тетради проектов помещено достаточное количество заготовок полей для всех игр, которые рассматриваются в курсе. Как и с запасными полями для Робика, с полями для игр ребята могут поступать по своему усмотрению: использовать в задачах как подсобный или запасной материал или играть на этих полях в настоящие игры.

Мы хотим научить ребят заканчивать решение любой задачи проверкой, в том числе и задачи на построение цепочки игры. Поэтому в указании приведены подсказки – условия, которые должны выполняться для любой правильно составленной цепочки позиций игры крестики-нолики. Обратите внимание на то, чтобы все ребята выполнили эту последнюю часть задания. Важно, чтобы уже в этой задаче ребята обратили внимание на то, что позиций в цепочке всегда на одну больше, чем сделано ходов в партии и подумали, почему. Ответ прост – добавляется начальная позиция – «нулевой ход». Подобные детали ребятам придется иметь в виду в дальнейшем при решении более сложных задач.

Вот один из возможных вариантов цепочки Р:

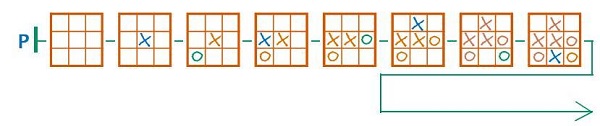
Задача 7. Здесь, в отличие от задачи 6, дан конец партии (а также, вторая позиция цепочки). Поэтому ребята могут двигаться либо от начала цепочки к концу, либо наоборот. В первом случае необходимо соблюдать правило – ставить только те знаки, которые есть в позиции, предшествующей заключительной (причем крестик, помеченный синим цветом использовать нельзя). Необходимо также следить за соблюдением очередности хода, за тем, чтобы на каждом ходу появлялся только один значок, и за тем, чтобы все значки аккуратно переносились с предыдущей позиции на следующую. Если кто-то из ребят решит двигаться от конца цепочки к началу, то он просто будет убирать по одному значку, учитывая очередность хода (конечно, не забывая о том, что один синий крестик должен быть убран первым, а другой – последним). В данном случае ответ на вопрос не зависит от того, как достроена цепочка, поэтому на него можно ответить сразу. В этой и последующих подобных задачах мы уже не напоминаем ребятам о том, что необходимые для решения поля можно найти на листе вырезания (оставляем лишь значок – ножницы).

Вот один из возможных вариантов цепочки H:

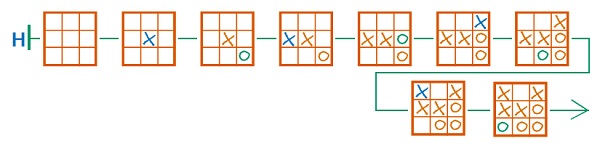
Задача 8. Необязательная. Здесь построение партии должно удовлетворять некоторому условию. Один из подходов состоит в том, чтобы решать задачу с конца: посмотреть, какой могла бы быть позиция в конце, а затем идти от этой позиции к начальной. Конечно, в последней позиции нельзя расставлять крестики и нолики как угодно. Какие имеются ограничения? Например, нельзя, чтобы ноликов было больше, чем крестиков, и чтобы их было на два меньше, чем крестиков, или еще меньше. Ясно, что поставленные уже в заданных позициях два крестика и нолик должны сохраниться. Ясно также, что в заключительной позиции не должно быть выигрышной комбинации для одного из игроков – ведь игра должна кончиться вничью.

Можно предложить и другой подход к решению такой задачи. Он будет естественным для ребят, которые достаточно много играли в крестики-нолики вне урока. Идея состоит в том, что если ход делает Первый, то «честно» играть за Первого, а если Второй – то за него. При этом главная задача – помешать выигрышу противника, а уж следующая – собственная победа. Ребята, знакомые с игрой, интуитивно понимают, что ничья получается именно так – когда противники «хорошо мешают друг другу». Отличие данной задачи от настоящей партии состоит в том, что даже если ученик случайно пропустит позицию, которая может привести к выигрышу Первого или Второго, то он всегда сможет вернуться обратно по цепочке позиций, найти свой ошибочный ход и начать «поправлять» игру с этого места. В настоящей же игре ребята видят свою ошибку только тогда, когда ее уже нельзя поправить: игра закончилась.

Обратите внимание всех ребят, что последним этапом решения является проверка того, нет ли в какой-нибудь позиции выигрышной комбинации для одного из игроков. На самом деле проверять нужно, начиная с шестой позиции, так как только в ней впервые появляется третий крестик и, соответственно, впервые может появиться выигрышная тройка крестиков.

Итак, при любом подходе ученику нужно сначала спланировать свое решение, нарисовать пробные позиции на черновике (например, на одном из пустых полей на листе вырезания), а затем уже начать вырезать, наклеивать и расставлять крестики и нолики. Как и раньше в подобных задачах, попросите детей ставить вновь появившийся крестик синим, а нолик зеленым.

Вот один из возможных вариантов цепочки M:

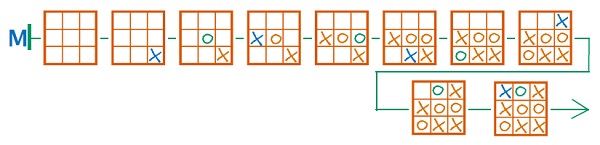
Задача 9. Повторение темы «Дерево». В задаче требуется внимательный анализ всех утверждений или большое число проб. Сопоставляя утверждения, убеждаемся, что на первом уровне не может быть ни круглых, ни треугольных бусин, иначе первое или второе утверждение не будет иметь смысла. На первом уровне должны быть только квадратные бусины, значит треугольные бусины могут быть не раньше второго уровня, а круглые – не раньше третьего. Следовательно, у искомого дерева не меньше трех уровней. При этом в мешке 8 бусин, а на каждом уровне дерева по 2 листа, значит уже для построения дерева из четырех уровней бусин не хватает. Вывод – в искомом дереве ровно три уровня бусин. Кроме того, в ходе этих рассуждений становится понятно, что вершины-бусины нужно экономить, иначе их не хватит для построения дерева. Поместим на первый уровень три квадратные бусины – два листа и один не лист, меньшим числом бусин на первом уровне не обойтись. Дальше дерево можно строить по-разному. Обязательно нужно поместить круглую бусину на третий уровень, перед ней – одну треугольную на второй. Напомните детям, что заканчиваться решение должно определением истинности всех утверждений для построенного дерева.

Задача 10. Не слишком сложная задача на повторение темы «Склеивание цепочек». Проверьте, все ли ребята помнят, что при склеивании с пустой цепочкой она просто пропадает. Так в третьем примере к слову приклеиваются две цепочки и получается то же самое слово. Значит, к слову приклеиваются две пустые цепочки.

Компьютерный урок «Цепочка позиций игры. Игра крестики-нолики», задачи 8 – 14

Задача 8. Несложная задача на усвоение правил игры в крестики-нолики. Для её решения достаточно сыграть на данном поле партию. Если кому-то покажется неправильным или неинтересным играть за двоих, можно предложить разбиться на пары и сыграть партии на бумаге, а затем перенести свои партии на экран. Конечно, проверить полностью соблюдение всех правил игры по заключительной позиции невозможно. В частности, сложно определить последовательность ходов и то, что ребёнок не продолжал играть, уже имея заключительную позицию на поле. Поэтому достаточно проверить выполнение следующих условий:

• На поле стоит поровну крестиков и ноликов, либо крестиков на один больше.
• На поле имеется ровно один ряд из трёх одинаковых значков, либо на поле ничья. Если на поле больше одного ряда из трёх одинаковых знаков, значит ребёнок в какой-то момент не заметил заключительную позицию и продолжал играть. Такие ситуации, конечно, могут быть и в реальной игре. Однако, поскольку эта задача учебная, нужно обязательно указать ребёнку на нарушение правил.

По окончании игры ребёнок должен обязательно проанализировать заключительную позицию, чтобы ответить на вопрос задачи.

Мы не предлагаем здесь детям никаких новых компьютерных инструментов – дети работают знакомым инструментом «карандаш».

Задача 9. Первая, несложная компьютерная задача о цепочке позиций игры в крестики-нолики. Конечно, первой позицией будет та, на которой не стоит ни одного значка – пустое поле. На второй позиции должен стоять один значок, на третьей – два и т. д. Таким образом решать задачу можно достаточно формально – переставлять позиции, опираясь лишь на число значков в них. Но не стоит это подсказывать детям – лучше, если они сами изобретут этот метод или какой-то другой.

После того как определилась заключительная позиция, можно отвечать на вопрос задачи. В данной партии выиграли нолики, то есть победил Второй игрок.

Ответ:

Задача 10. Эта задача гораздо сложнее предыдущей. Ребенку, которому будет трудно начать решение, посоветуйте начать с заключительной позиции цепочки. Нужно выбрать позиции, которые можно считать заключительными, и попытаться построить цепочку партии игры от конца к началу цепочки.

Вот два возможных варианта решения:

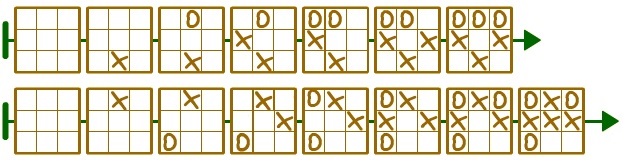
Задача 11. Повторяем терминологию, связанную с деревьями, вспоминаем, как пользоваться компьютерным инструментом «дерево».

Задача 12. Повторяем понятия «путь дерева» и «перед каждой/после каждой» для бусин дерева. Обратите внимание: для некоторых путей условие с понятиями «перед каждой/после каждой» не имеет смысла, поскольку либо круглой бусины в них нет, либо она является листом и не имеет следующей. В качестве ответа подходит ровно один путь – тот, который заканчивается жёлтым треугольным листом.

Задача 13. Повторение операции склеивания мешков цепочек. Нетрудно сосчитать, что в мешке-результате будет 2 • 6 = 12 цепочек, значит все окна должны быть заполнены. Важно не забыть, что склеивание с пустой цепочкой даёт в результате ту же цепочку (слово с пустым окончанием).

По окончании решения можно спросить детей с точки зрения курса русского языка: «Какие цепочки лежат в каждом из мешков?» В первом мешке лежат основы русских существительных мужского рода, во втором мешке — окончания таких существительных при изменении падежа. Таким образом, в мешке-результате лежат все формы этих двух существительных при склонении по падежам.

Задача 14. Повторение понятий «одинаковые мешки», «разные мешки» и повторение различия между количеством монет и количеством рублей. Дети обычно решают такие задачи методом проб и ошибок, пытаясь строить мешки без какой-либо системы и просто сравнивая после каждого шага новый мешок со всеми уже построенными. Взрослые же и наиболее сильные учащиеся обычно используют в таких задачах перебор, чтобы обеспечить условие того, что все мешки действительно разные. Учитывая имеющиеся в библиотеке этой задачи монеты, выясняем, что во всех трёх мешках будет присутствовать один и тот же набор монет, составляющих в сумме 11 рублей: 5 + 2 + 2 + 2. А варьировать можно только наборы монет, составляющих 10 рублей ― 1 десятирублёвая, 2 пятирублёвые, 5 двухрублёвых.