Информатика. 3 класс Демо+методичка

Урок 30. Проект «Турниры и соревнования», 1–2 часть

Материалы к проекту: задачи 2 – 5 на с. 6 – 9 тетради проектов, заготовки для турнирной таблицы и дерева турнира на с. 10 – 13 тетради проектов.

Общее обсуждение

Как и большинство проектов курса, данный проект стоит начать с общего обсуждения, в ходе которого дети должны получить представление о двух видах турниров (круговом и кубковом), их сходствах и различиях, основных правилах их проведения.

Весь мир постоянно соревнуется. Различным соревнованиям (спортивным и не только) отводится большое место в жизни людей. Спортивные соревнования проводятся по разным правилам, но мы не будем заниматься правилами конкретных видов спорта и игр (хоккей, бег или камешки), а обсудим, как выявляется победитель.

Существует много вариантов определения победителя в состязаниях. Попросите детей вспомнить или придумать правила выявления лучшего в различных состязаниях: бег, спортивные игры, прыжки в высоту, прыжки в длину.

Затем ограничьте задачу играми, в которых два человека или две команды встречаются между собой. Для начала лучше считать, что такие встречи заканчиваются обязательно победой одной или другой стороны. В паре всегда будут выигравший и проигравший. Но людей у нас не двое, а целый класс. Как определить лучшего?

Скорее всего, дети (особенно мальчики) знают, что на соревнованиях либо каждый участник встречается с каждым (как в первенстве страны по футболу), либо проигравший сразу выбывает (так разыгрывают кубок страны, так проходят соревнования по теннису).

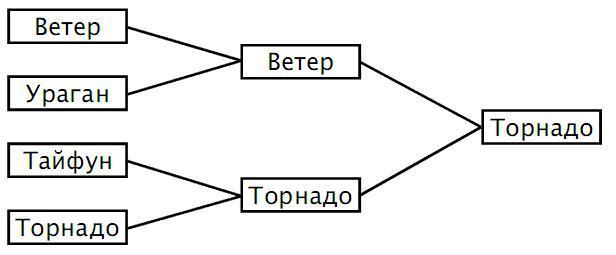
Круговой турнир, в котором все соперники встречаются между собой, изображается в виде таблицы. Кубковый турнир удобно наглядно представить в виде дерева:

Увлекающиеся спортивными зрелищами ребята могут сказать, что часто в соревнованиях сначала проводятся круговые турниры в группах, а затем победители или призеры групп играют кубковые матчи на выбывание. Такой вариант соревнования можно изобразить в виде дерева, листья которого содержат таблицы круговых турниров.

Выслушав все, что известно детям, обсудите, какие схемы они считают справедливыми, а какие нет. В этом обсуждении стоит отдельно рассмотреть два случая.

1. Более реальный – победитель игры в паре заранее неизвестен. Именно так обстоит дело в огромном большинстве игр и состязаний, поскольку все они имеют элемент случайности.
2. Менее реальный – силы соревнующихся очень разные, и мы заранее знаем, кто в какой паре победит.

Дети, скорее всего, скажут, что круговой турнир более справедливый, чем кубковый. Можно не выяснять сейчас, в чем справедливее и почему они так считают, а оставить это обсуждение до окончания проекта.

Решение задач из тетради проектов

Основным содержанием данного проекта является решение задач из тетради проектов. Именно в ходе этой работы ребята должны усвоить правила проведения турниров (кругового и кубкового) и научиться оформлять их результаты в виде турнирной таблицы или дерева.

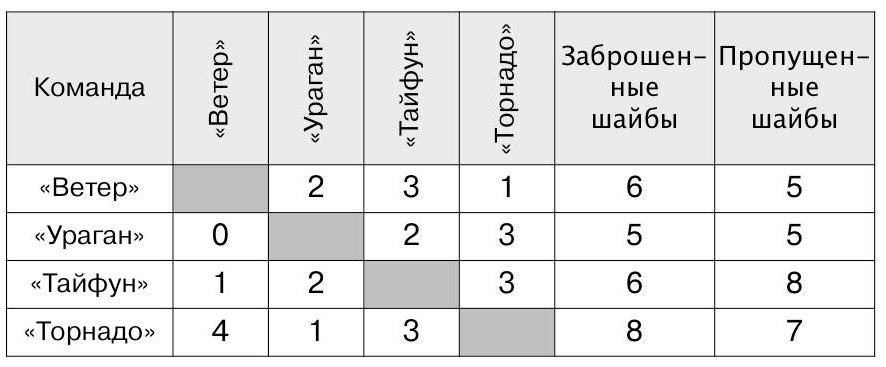
Задача 2. В этой задаче ребята увидят две таблицы для одного кругового турнира. Действительно, таблицу кругового турнира можно составлять по-разному. Так по таблице 1 проще подсчитывать заброшенные шайбы (сумма чисел в соответствующей строке) и пропущенные шайбы (сумма чисел в соответствующем столбце). По таблице 2 проще подсчитывать набранные очки и выяснять места для каждой команды. Вот заполненные таблицы 1 и 2:

Таблица 1.

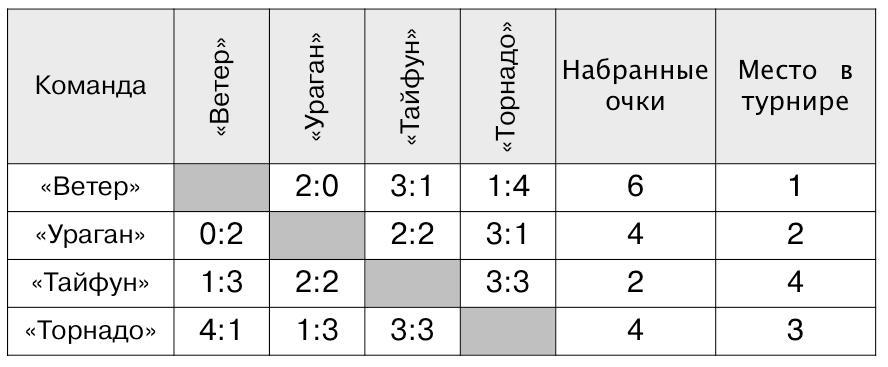
Таблица 2.

При заполнении таблицы 2 ребята столкнутся со сложным случаем распределения мест. Команды «Ураган» и «Торнадо» имеют по 4 очка. Команда «Ураган» при этом заняла более высокое (второе) место, поскольку выиграла во встрече с командой «Торнадо» (со счетом 3:1).

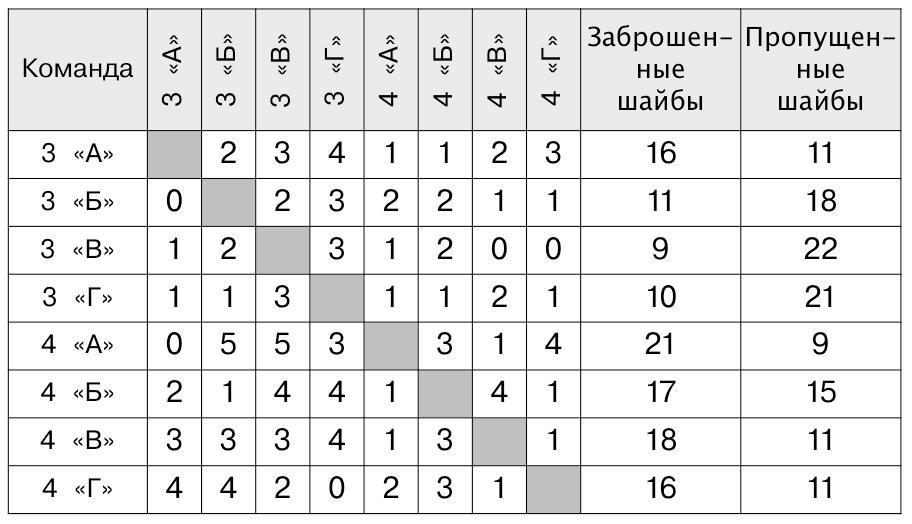
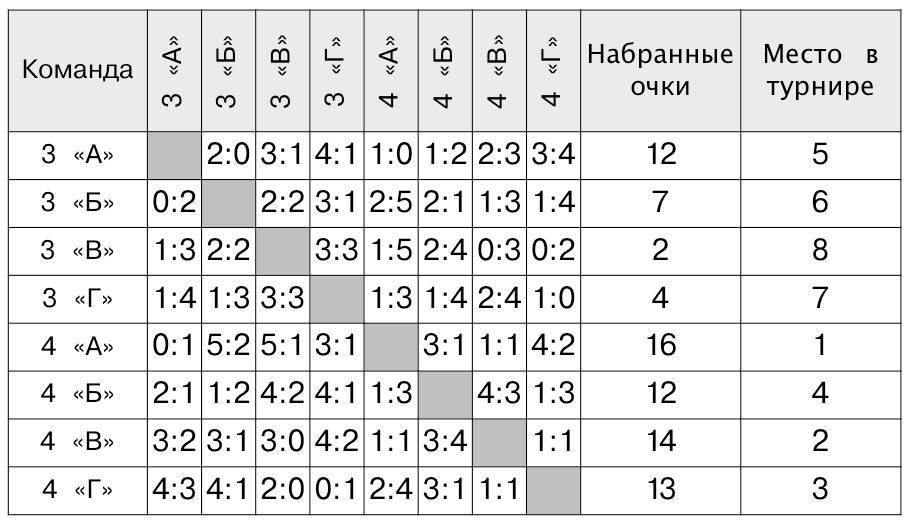
Задача 3. Эта задача снова посвящена круговому турниру, только команд в нем участвует гораздо больше и это затрудняет работу с турнирными таблицами. Эта задача сложнее предыдущей еще и тем, что придется использовать одновременно информацию из двух таблиц. Кроме того, для решения необходимо понимать взаимосвязь и правила построения обеих таблиц. Лучше начать с того, что в обеих таблицах заполнить первые 8 столбцов (со счетом). Например, первая строка таблицы 4 позволяет заполнить первую строку и первый столбец таблицы 3 – записать заброшенные и пропущенные шайбы командой 3 «А» класса. После этого можно заполнить все остальные пустые клетки в таблицах. Мы приводим здесь заполненные таблицы 3 и 4:

Таблица 3.

Таблица 4.

Кроме заполнения таблиц, ребята должны ответить на вопросы. Ответ на первый вопрос можно найти разными способами. Один из вариантов – вычислить при помощи рассуждений. Каждая из 8 команд играла с каждой из оставшихся 7 команд, значит, надо перемножить 7 и 8. Но при этом каждый матч был посчитан дважды, поэтому результат надо разделить на 2 и получится число игр. Другой вариант – просто сосчитать число клеток со счетом, которые располагаются выше диагонального ряда (или сосчитать все клетки со счетом, кроме диагональных, и разделить результат на 2).

Ответ на второй вопрос задачи можно найти в таблице 4, а на третий – в таблице 3.

Задача 4. Эта задача посвящена кубковому турниру. Здесь ребята смогут убедиться, насколько быстрее его проводить и легче подводить итоги. Фактически итоги подводятся автоматически, ведь итогом такого турнира является победа в самой последней игре. Результаты всех игр при решении этой задачи ребята будут брать из таблицы 4 (задачи 3). Например, в игре между командами 3 «А» и 4 «А» выиграл 3 «А», значит, команда этого класса и вышла в следующий тур, а в вершину дерева предыдущую перед парой 3 «А» и 4 «А» надо записать 3 «А».

Сравнивая результаты решения этой и предыдущей задач ребята могут убедиться, что в турнирах, проводимых по разным системам, могут быть разные победители – даже при одинаковых результатах игр. Так в кубковом турнире уже в первом круге выйдет из борьбы победитель кругового турнира – 4 «А» класс. В результате победителем кубкового турнира становится 4 «В» класс.

Задача 5. В этой задаче ребята могут увидеть, что при проведении кубкового турнира победа одного из участников в значительной степени зависит от распределения участников по парам. Так, даже при очень стабильной игре в каждой паре игроков (как в данном случае) победитель турнира меняется в зависимости от того, как игроки расставлены в пары.

Идея решения этой задачи довольно проста. Если необходимо, чтобы выиграл Володя, ни в каком туре не надо его ставить в пары с игроком, которому он проигрывает – Колей. В частности, надо позаботиться о том, чтобы Коля не вышел во второй тур и поставить его в первом туре играть с Петей. Аналогично ситуация будет складываться при выполнении второго задания. Что касается третьего задания, выполнить его невозможно, ведь Коля выигрывает только у одного игрока, а для победы ему надо сыграть две партии.

Продолжение проекта

Проведение турниров в классе

Данный проект запланирован в курсе 3 класса в рамках одного часа. Если у вас очень сильный класс, в конце урока может остаться 5 – 10 минут на проведение кругового или кубкового турнира в классе. Для это вы можете использовать турнирную таблицу на с. 10 – 11 и дерево турнира на с. 12 – 13. Если времени на это не останется – не страшно: в курсе 4 класса запланирована вторая часть проекта «Турниры и соревнования», которая как раз и будет состоять в проведении турниров в классе.

Ниже приводится описание нескольких игр, математическое содержание которых будет рассматриваться в курсе 4 класса. Можно предложить детям посоревноваться в умении играть в некоторые из этих игр или взять заведомо известные ребятам игры. Конечно, выбирать нужно такие игры, в которых не существует простого способа выигрыша или он не известен детям. Если в школе проводится какой-то спортивный турнир, можно использовать его результаты.

Кубковый турнир за 10 минут провести вполне реально. Если в классе меньше 32 учащихся (например, 25), проще всего выбрать 16 участников турнира, а остальных назначить контролерами. В этом случае последний уровень вершин дерева на странице 12 нужно аккуратно зачеркнуть.

Круговой турнир потребует значительно большего времени. Если в классе 30 человек, то по круговой системе надо будет проводить очень большое число игр – более 400. Если у вас нет возможности отвести на данный проект дополнительный урок, можно играть после уроков или на переменах, или разбиться на группы и устроить круговые турниры в группах, а среди победителей провести кубковый турнир для определения сильнейшего в классе. Можно придумать и другие варианты работы. Например, у вас в классе 23 человека. Можно 16 из них сделать участниками кубкового турнира, а остальные 7 учеников будут проводить круговой турнир в своей группе. Чтобы выяснить, кто победит в классе, два победителя турниров сыграют между собой.

Дополнение. Игра камешки

В эту игру часто играют дети, используется она и в различных соревнованиях на смекалку. Вы можете использовать эту игру при работе с проектом «Турниры и соревнования».

Правила игры такие. Перед двумя играющими кладется кучка камешков. Из этой кучки за один ход игрок берет не меньше одного, но не больше некоторого, заранее оговоренного числа камешков. Игроки делают ходы по очереди. Пропускать ход нельзя. Тот, кто сделает последний ход, выиграл. Игрок, которому при очередном ходе брать нечего, проиграл. Обычно разрешается брать 1, 2 или 3 камешка.

Вот еще три варианта игры.

1. Из кучи можно брать 1, 2 или 3 камешка. Выигрывает тот игрок, у которого в конце игры на руках оказывается четное число камешков.
2. Камешки лежат в двух кучках. За один ход можно брать любое число камешков, но только из одной кучки. Выигрывает тот, кто делает последний ход.
3. Камешки лежат рядами. В первом ряду 3 камешка, во втором ряду 5, а в третьем ряду 7 камешков. За один ход можно брать любое число камешков, но только из одного ряда. Выигрывает тот, кто делает последний ход.

Игре камешки будет посвящено много времени в курсе 4 класса.

Заключение

Умение правильно организовывать деятельность группы людей для решения общей задачи и точно выполнять отведенную тебе роль – важный для общества результат обучения. Развитие этих умений – еще одна педагогическая цель проектов.

В процессе выполнения проектов учащиеся выступают и как организаторы – в момент выработки стратегии сортировки или стратегий победы в игре, и как исполнители – занимаясь сортировкой по заранее придуманному алгоритму. Попеременное исполнение учеником этих ролей – организатора и исполнителя – очень полезно.