Информатика. 3 класс Демо+методичка

Урок 29. Таблица для склеивания мешков цепочек

К этому уроку у ребят имеется достаточно большой опыт склеивания мешков. В частности, дети уже убедились в том, что чем больше цепочек в мешках при склеивании, тем сложнее его осуществить, не сделав ошибок. Действительно, поскольку при склеивании каждая цепочка из первого мешка должна быть склеена с каждой цепочкой из второго мешка, то чем больше цепочек, тем больше комбинаций. В комментарии к предыдущему листу определений мы предлагали способ перебора цепочек в мешках, позволяющий не потерять решений и не добавить лишних. Но детям будет сложно его использовать, когда число цепочек в мешках будет больше трех, необходим более сильный инструмент. Для склеивания двух мешков таким инструментом является таблица. Ее применение делает процесс перебора цепочек и их попарного комбинирования максимально наглядным. В этом случае практически невозможно пропустить цепочку или написать лишнюю, поскольку цепочек в мешке-результате ровно столько, сколько клеток в таблице (не считая шапки, конечно). Таким образом, каждой клетке, находящейся на пересечении k-й строки и n-го столбца, соответствует ровно одна цепочка, которая является результатом приклеивания к цепочке, расположенной в k-й строке, и цепочки, расположенной в n-м столбце.

При использовании таблицы задачу на склеивание приходится решать немного дольше чем обычно, ведь цепочки приходится рисовать дважды – сначала в таблицу, а потом в мешок. Но это компенсируется тем, что долгая и тщательная проверка потом не потребуется.

Решение задач из учебника

Задача 177. Эта задача, по сути, повторяет лист определений и является наиболее важной на данном уроке. Дети должны сделать ее самостоятельно, даже если на это уйдет много времени. Вероятность неправильно заполнить таблицу минимальна, причем ошибку будет легко найти. Кто-то из детей может потерять решения при переписывании слов из таблицы в мешок. Чтобы этого избежать, можно соединять одинаковые слова в таблице и в мешке в пары или использовать пометки.

Задача 178. Если выписать все пути дерева F по порядку (по порядку следования листов в дереве сверху вниз), получится отрывок из стихотворения Д. Хармса и С. Маршака «Сорок четыре веселых чижа».

Задача 179. По содержанию задача аналогична задаче 176 – здесь тоже надо найти недостающие слова в мешках при склеивании. Эта задача наглядно показывает, насколько проще использовать в решении таблицу. Действительно, рассмотрим слова первой строки. Берем любое слово, для которого известно его окончание. Отсюда сразу находим основу. Аналогично можно найти все неизвестные цепочки первого мешка. Теперь рассмотрим четвертый столбец. Берем из него любое слово, отрезаем уже известную основу и получаем искомое окончание. Аналогично находим второе неизвестное окончание. Мешки Y и G теперь известны, и задача становится аналогична задаче 177.

Задача 180. Мы выяснили, что для склеивания двух мешков очень удобно использовать таблицу. Однако она не поможет, если взять три или более мешка. В таком случае удобно строить дерево (конечно, дерево можно было строить и для двух мешков). На первом уровне этого дерева располагаем все цепочки из первого мешка, за каждой вершиной первого уровня ставим все цепочки из второго мешка, за каждой вершиной второго уровня – все цепочки из третьего мешка. Теперь, чтобы выписать по этому дереву искомый мешок, нужно выписать все его пути, одновременно склеивая все вершины (цепочки букв) каждого пути. Например, первый путь дерева выглядит так: БЛИЗ–ЕНЬК–АЯ, когда мы выписываем этот путь, сразу склеиваем все вершины (в порядке их следования) и получаем слово БЛИЗЕНЬКАЯ.

Задача 181. Необязательная. Работая со вторым утверждением, ребята встретятся с новым для них типом толкований – избыточным толкованием. Такое утверждение добавляет к информации толкового словаря нечто от себя. Предположим, в словаре есть толкование: «Клест – небольшая лесная птица», а в задании приведено утверждение: «Клест – небольшая лесная птица с перекрещивающимися концами клюва». Такое толкование может быть и истинным, и ложным, в зависимости от того, соответствуют ли новые подробности действительности (в данном примере оно истинно). Часто мы никак не можем проверить эту новую информацию, поэтому не можем определить, истинно или ложно это утверждение. Можно просто написать в окне букву Н – нам это неизвестно. Вполне возможно, что некоторые ребята так и поступят.

Иногда избыточные толкования включением новых деталей отбрасывают часть объема понятия, которая к нему в действительности относится. В результате толкование становится ложным, поскольку оно уже не отражает все то понятие, которое описывает. Примером может служить утверждение в задаче: «Дефицит – это недостаток, нехватка лимонада». Сравнивая утверждение с толкованием слова «дефицит» в словаре, мы понимаем, что объем понятия стал слишком узким и не соответствует толкованию в словаре. Из него следует, что это понятие уже не применимо к колбасе, рабочей силе, времени и т. д. Но мы знаем, что на самом деле оно применимо и поэтому можем написать в окне букву Л.

Задача 182. Эта задача несложная, поскольку на самом деле неизвестным оказывается лишь первый мешок. Действительно, слова в мешке-результате можно написать сразу – известно, что это числительные от 11 до 19. После этого легко написать цепочки в первом мешке, если от каждого слова-числительного отрезать цепочки НА-ДЦАТЬ.

Задача 183. Необязательная.

Ответ: фигурки C и L одинаковые.

Компьютерный урок «Таблица для склеивания мешков цепочек», задачи 170-177

Задача 170. Эта задача, по сути, повторяет лист определений и является наиболее важной на данном уроке. Дети должны решить ее самостоятельно, даже если на это уйдет много времени. Вероятность неправильного заполнения таблицы минимальна, причем ошибку будет легко найти. Кто-то из детей может сделать ошибку при переносе бусин в таблицу, поскольку бусины нужного цвета придется искать прокруткой. Чтобы этого избежать, можно предложить детям останавливаться после каждого переноса и проверять себя.

Задача 171. Задача аналогичная задаче 170, но в данном случае используются не бусины, а основы русских слов в именах строк и окончания в именах столбцов, В результате склеивания получатся русские слова, точнее говоря прилагательные  различных родов. Скорее всего, задача также не вызовет затруднений и будет выполнена всеми учащимися.

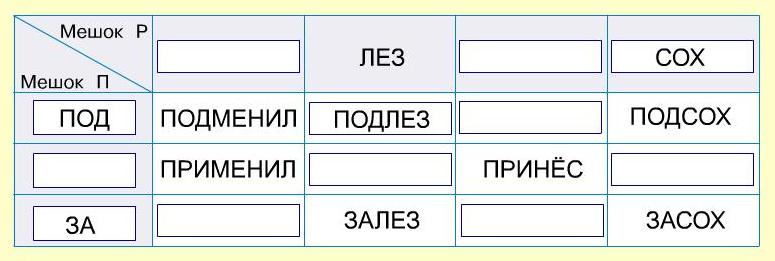
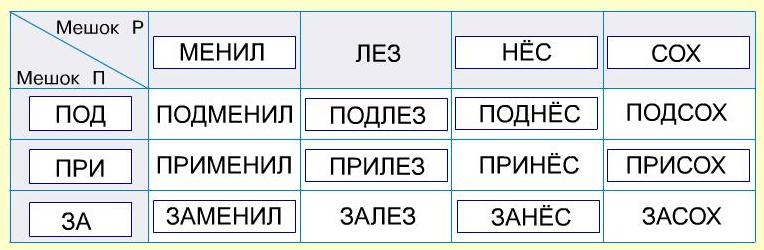
Задача 172.  По содержанию задача уже знакома ребятам, здесь надо найти недостающие слова в мешках при склеивании, а для этого сначала определить, какие части слов стоят в окнах в именах столбцов и именах строк. Будем опираться на те части, которые нам известны: из данных второго столбца (имя столбца ЛЕЗ, а слово ЗАЛЕЗ) делаем вывод, что имя третьей строки – ЗА. Теперь из данных третьей строки (имя строки ЗА, слово ЗАСОХ) находим имя четвертого столбца – СОХ. Теперь из данных четвертого столбца (имя столбца СОХ, слово ПОДСОХ) находим имя первой строки – ПОД и составляем слово ПОДЛЕЗ.

Из данных первой строки (имя строки ПОД, слово ПОДМЕНИЛ) находим имя первого столбца – МЕНИЛ и составляем слово ЗАМЕНИЛ. Из данных первого столбца (имя столбца МЕНИЛ, слово ПРИМЕНИЛ) находим имя второй строки – ПРИ, составляем слова ПРИЛЕЗ, ПРИСОХ. Из второй строки (имя ПРИ, слово ПРИНЁС) находим имя третьего столбца – НЁС, составляем слова ПОДНЁС и ЗАНЁС.

Задача 173.  Задача на повторение операции склеивания мешков цепочек. Ясно, что наиболее длинная цепочка (цепочка длины 3) должна лежать в мешке-результате. Теперь найдем две цепочки, при склеивании которых получается такая цепочка. Это цепочка из одной зеленой бусины и любая цепочка длины 2 (все они одинаковые). Положим цепочку из одной зеленой бусины в первый мешок, а одну цепочку длины 2 – во второй. Ясно, что цепочку из одной красной бусины нужно положить во второй мешок, ведь она во всех цепочках стоит на последнем месте. Так продолжаем рассуждать дальше, пока все цепочки не оказываются в мешках.

Задача 174. К настоящему моменту дети решили довольно много аналогичных задач. Однако не стоит предлагать её слабым детям, которые до сих пор решают подобные задачи простым перебором клеток поля – перебор здесь слишком велик, и ребёнок потеряет с этой задачей слишком много времени. При необходимости попытайтесь вместе с ребёнком проанализировать программу и порассуждать, как уменьшить перебор.

Задача 175.  Мы выяснили, что для склеивания двух мешков очень удобно использовать таблицу. Однако она не поможет, если взять три или более мешка. В таком случае удобно строить дерево (конечно, дерево можно было строить и для двух мешков). На первом уровне этого дерева располагаем все цепочки из первого мешка, за каждой вершиной первого уровня ставим все цепочки из второго мешка, за каждой вершиной второго уровня – все цепочки из третьего мешка. Теперь, чтобы выписать по этому дереву искомый мешок, нужно выписать все его пути, одновременно склеивая все вершины (цепочки букв) каждого пути. Например, первый путь дерева выглядит так: ВЕТ–К–И, когда мы выписываем этот путь, сразу склеиваем все вершины (в порядке их следования) и получаем слово ВЕТКИ.

Задача 176.  Задача на повторение листа определений «Перед каждой бусиной. После каждой бусины», аналогичная компьютерной задаче 129.

Задача 177. Необязательная.  Задача на нахождение трех одинаковых фигурок. Фигурки очень сложные, кроме того имеется большое количество парных повторений поэтому данное задание можно предложить ученикам в качестве дополнительного, если остается свободное время на уроке.