Информатика. 3 класс Демо+методичка

Уроки 25–26. Проект «Сортировка слиянием»

Материалы к проекту: по одному комплекту карточек на учащегося из вкладыша тетради проектов, с. I – XVI, XLI – LVI; зерна риса и гречки, горох и фасоль, бусины, детали ЛЕГО и т. п.

Несколько слов о сортировке информации

В информатике сортировкой называется наведение порядка в информации. Разберемся, какие виды сортировок нам могут понадобиться, и постараемся понять, что в них общего, а чем они различаются.

Рассмотрим это на примере списка учеников класса. В журнале список приводится в словарном порядке. Чтобы такой список появился, классный руководитель и секретарь школы проделали некоторые манипуляции: может быть, просто нажимали кнопки на компьютере, а возможно, раскладывали личные дела. На линейке 1 сентября и на уроках физкультуры во многих школах принято выстраивать детей по росту, а чтобы не забыть поздравить ребенка с днем рождения, удобно иметь список детей в порядке их дат рождения. Во всех приведенных случаях наводился определенный порядок по заранее выбранному правилу. Операцию по наведению порядка будем называть упорядочением. В терминологии курса можно говорить, что при упорядочении объекты выстраиваются в цепочку.

В процессе выполнения проектов мы постарались разобраться в способах упорядочения информации. При упорядочении все элементы списка выстраиваются в цепочку друг за другом в соответствии с заранее выбранным правилом. Но часто нужно не расставлять учеников в каком-то порядке, а объединить их в некоторые группы опять же по заранее установленным правилам (признакам): мальчики – девочки, отличники – хорошисты – троечники – двоечники, дети из полных семей – дети из неполных семей, общее любимое блюдо, близко живущие дети, болельщики одной команды и т. д. Операцию по объединению в группы будем называть группировкой. В терминологии курса можно говорить, что при группировке объекты раскладываются в мешки по определенным правилам.

На первый взгляд между упорядочением и группировкой мало общего, но на самом деле это не так. В большинстве случаев нас действительно не интересует порядок, в котором мы рассматриваем результаты группировки. Не имеет значения, кто стоит впереди – мальчики или девочки – и в каком порядке рассматривать отличников, троечников и хорошистов. Важно только, что они объединены в группы. Но попробуем проследить, как мы группируем учеников. Мы обязательно вырабатываем для себя некоторый порядок. Например, в левый столбик выписываем фамилии отличников, правее – хорошистов, еще правее – учеников с одной тройкой и т. д. Затем начинаем в столбики вписывать фамилии. Зрительно у нас снова получаются цепочки (ведь в каждом столбике слова идут друг за другом), но здесь порядок слов нам неважен.

При упорядочении учеников у нас тоже могло получиться так, что два или более  учеников имеют одинаковые фамилии, имена и отчества или совпадающий день рождения. В этом случае согласно установленным правилам упорядочения из них нельзя выбрать идущего раньше, поэтому получится маленький мешок с фамилиями нескольких учеников. Мы, конечно, впишем их в цепочку в произвольном порядке.

Из приведенных примеров понятно, что процессы упорядочения и группировки имеют очень много общего. Отличаться будет отношение к результату. При группировке существенно только, в какой мешок (группу) попала фамилия, а при упорядочении важна последовательность. Упорядочение часто является способом (элементом) сортировки. Так, в списке, упорядоченном по датам рождения, легко выделить группы учеников, родившихся в разные времена года. Или наоборот, проводя упорядочение по алфавиту, часто бывает удобно сначала сгруппировать фамилии по первым буквам, а затем уже упорядочивать их в группах.

В математике понятие сортировка объединяет понятия упорядочение и группировка. Мы также используем только термин сортировка, иногда уточняя: «Сортировать в алфавитном порядке».

Описание проекта

Умение ориентироваться в больших массивах информации является важнейшим в век информационных технологий. Прежде всего нужно иметь возможность легко находить информацию, соответствующую определенным критериям, сортировать и группировать ее по определенным правилам. В современной повседневной жизни основную черновую работу по обработке больших массивов информации проводят компьютеры. Выполнять ее вместо компьютера в реальной жизни нам не надо, но чтобы правильно интерпретировать результаты работы компьютеров и должным образом подготовить запрос для компьютера (правильно поставить задачу поиска и обработки информации), важно понимать, как они это делают. Знакомству с алгоритмом сортировки и посвящен настоящий проект. Часто в жизни бывают моменты, когда требуется расставить или разложить в заданном порядке различные предметы (книги, тетрадки). Такую работу не удастся передать компьютеру.

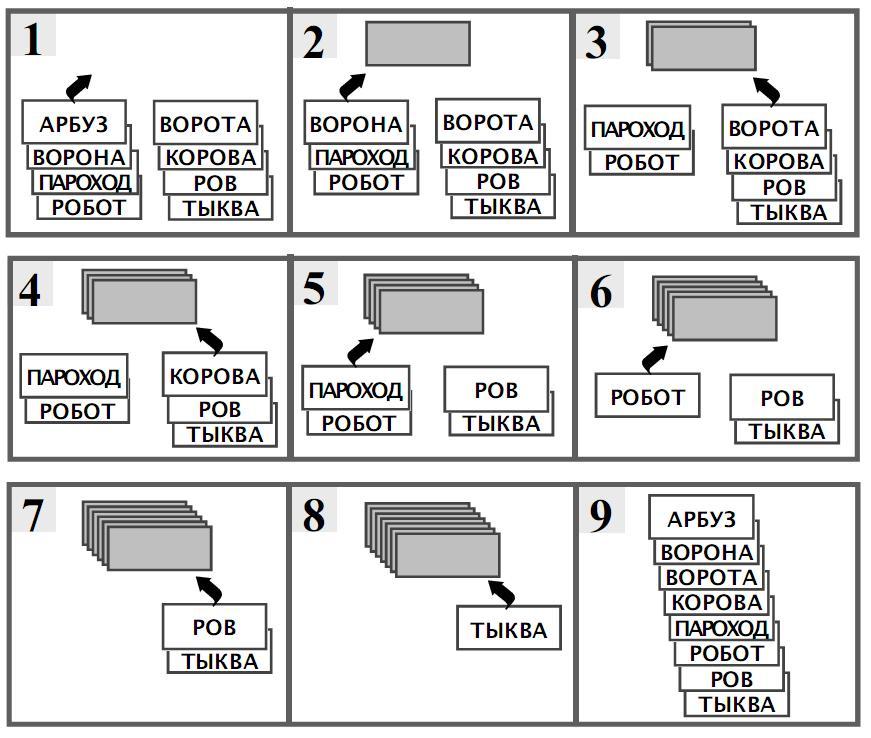
При выполнении предыдущего проекта учащиеся познакомились с устройством «настоящих» словарей, иначе говоря – с сущностью словарного (лексикографического) порядка. Дети уже умеют расставить в алфавитном порядке небольшое количество слов и объяснить, почему слово арбуз идет перед словом ворота, а слово ворота идет после слова ворона. Вы с детьми, скорее всего, еще не обсуждали стратегию, используя которую можно быстро и безошибочно расположить все слова в словарном порядке. Обычно достаточно просто просмотреть все слова, выбрать первое по алфавиту, из оставшихся слов выбрать второе и т. д. Способ, каким выбирается очередное слово, тоже как правило раньше не обсуждался, потому что для маленького списка слов не возникало такой проблемы. Обычно дети, проговаривая про себя или тихо вслух алфавит (а может быть, и со зрительной опорой на напечатанный алфавит), пробегают глазами все слова и ищут, нет ли среди них слова на очередную букву. Если такое слово есть, его ставят в цепочку. Постепенно формируется упорядоченная по алфавиту цепочка слов. Если на очередную букву будет больше одного слова, начинают разбираться с ними по второй букве.

Теперь усложним задачу. Попросим расположить в алфавитном порядке весьма значительный массив слов: 16 листов по 24 карточки – это 384 слова. Количественное увеличение слов в данном случае приводит к качественным изменениям (попробуйте подумать, к каким именно, прежде чем продолжите читать текст). Из 384 слов уже нельзя увидеть сразу все и даже найти первое из них – не простая задача. Методика, интуитивно используемая детьми при сортировке небольшого числа слов, здесь неприменима.

Приступая к выполнению проекта, выньте листы вкладыша из одной тетради проектов и вырежьте из них отдельные карточки. Каждый ребенок имеет в тетради проектов полный список всех слов, что позволит ему заняться их сортировкой и дома вместе с родителями; в классе же на первых порах рекомендуется использовать только один набор слов. Можно попробовать поставить задачу сортировки, не давая сначала никаких руководящих указаний, и понаблюдать, что и как ребята будут делать.

Даже если дети организованные и рабочее место в классе позволяет всем собраться вокруг одного стола, дело будет продвигаться медленно. И главное здесь, что увеличение объема работы приводит к необходимости изменить способы ее выполнения. В большой куче не удастся увидеть сразу все слова, поэтому нельзя, просто просматривая их, найти первое из них. Надо придумать способ, который позволит отыскать такое слово, про которое мы сможем уверенно сказать, что оно первое. Для этого следует обсудить с детьми, что они делают, разыскивая первое слово среди небольшого массива слов. Проговаривая, как они ищут слово, одновременно с перекладыванием и передвижением карточек, дети убеждаются в том, что они наводят при этом определенный порядок и действуют по конкретному алгоритму.

При сортировке большого массива возникают два вопроса:

1. Какую выбрать стратегию сортировки? Существует много разных алгоритмов сортировки различной информации при создании компьютерных программ. Работая в проекте, учащиеся проведут сортировку разными способами и попробуют понять их преимущества и недостатки.
2. Как правильно распределить работу? Когда на долю человека выпадает очень много работы, он зовет себе на помощь других людей и они делают ее вместе. Но, работая вместе, нужно уметь договориться о том, кто что будет делать. Ведь может получиться так, что люди будут не помогать, а только мешать друг другу. Не исключено, что работать будут только один или два человека, а остальные – наблюдать. Обучаясь в этом проекте организации совместной параллельной работы людей над общей задачей (что само по себе очень важно), мы познаем и то, как это делают компьютеры.

Прежде чем приступить собственно к выполнению проекта, следует провести подготовительную работу:

1. Повторить с детьми алфавит.
2. Поиграть всем классом в игру со словами, например в такую: узнать, какое слово из пары идет раньше в словаре: ворота или собака, ворота или ворона, чашка или шапка. Наибольшие затруднения у детей обычно вызывают буквы второй половины алфавита.
3. Нарезать карточки со словами из тетради проектов (1 экземпляр). С карточками можно будет провести несколько разных проектов. Можно дополнительно самим изготовить и другие наборы карточек, например со словарными словами или словами на различные правила. Их можно будет использовать не только при сортировке, но и при повторении различных тем по русскому языку.

Повторение алфавита

Фронтальная работа. На доске написан русский алфавит, но некоторые буквы пропущены. Пропуск обозначен многоточием, причем число пропущенных букв соответствует числу многоточий. Нужно назвать пропущенные буквы (надпись на доске вначале закрыта, учитель открывает ее в нужный момент).

А ... ... Г... Е Ё ... ... И Й ...  Л ...  Н ... П Р ... ... У ... Х Ц Ч ... Щ Ъ ... ... Э ... Я

Учитель. Закройте глаза и представьте расположение букв в алфавите. Может быть, кто-то из вас про себя проговорит, как расположены буквы в алфавите. Откройте глаза и посмотрите на доску. Что вы видите?

Дети. Буквы русского алфавита. Они стоят в алфавитном порядке, но некоторые буквы пропущены.

(На самом деле дети видят часть алфавита, а что пропущено – это удел фантазии. На этом этапе любая фантазия детей будет правильным ответом. Например, могут быть пропущены картинки. Хорошо, если дети предложат какие-то варианты, отличные от стандартного, – не буквы алфавита. Любое предложение детей следует принять.)

Учитель. Я написал алфавит, а затем часть букв стер. От каждой стертой буквы остались только точки. Кто может назвать пропущенные буквы в том порядке, в котором они должны идти в алфавите?

Дети. Б, В, Д, Ж, З, К, М, О, С, Т, Ф, Щ, Ы, Ь, Ю.
(По мере того как дети называют буквы, учитель вписывает их в алфавит на доске. В другом варианте вызванный к доске ученик вписывает буквы, а дети класса проверяют запись.)

Следующий, более сложный этап состоит в том, что на доске предлагается запись алфавита с пропущенными буквами, но пропуски не обозначены, так что неизвестно, сколько букв пропущено:

Б       Д       Ж       З       К       М       О       С       Т       Ф       Ш       Ы       Ю

Учитель. Посоветуйтесь с соседом и примите решение, какие буквы пропущены.

(Дети вслух обсуждают между собой и восстанавливают цепочку алфавита. Затем один человек – по выбору учителя из всех желающих – выходит к доске и вносит изменения, дописывая ниже цепочку пропущенных букв. Остальные внимательно следят и при необходимости вносят коррективы.)

Индивидуальная работа. Учащимся раздают листы бумаги, на которых они по памяти пишут русский алфавит, затем проверяют свою работу по настенной таблице, либо по записи на доске, либо по словарю и т. п. (особенность состоит в том, что ребенок работает совершенно самостоятельно, углубившись в собственные воспоминания и самопроверку). Если не все сразу получится, следует внести изменения и повторить упражнение еще раз.

Работа в группах. Перемешанные буквы (из магнитной азбуки, из конструктора, вырезанные из картона) раскладываются в алфавитном порядке. Делается это так. Учитель высыпает в беспорядке буквы алфавита (по одному экземпляру каждой буквы). Каждый ребенок в группе из 12 – 15 детей берет себе по 2 – 3 буквы (в произвольном порядке). Затем по команде учителя дети в каждой группе начинают раскладывать все буквы в алфавитном порядке. В этой игре дети должны одновременно решать несколько важных задач как содержательного (повторение алфавита), так и коммуникативного характера (умение услышать друг друга и договориться). Проверять данную работу может либо учитель, либо другая группа детей.

Задача окажется более сложной, если учитель положит на столе некоторые буквы не в одном экземпляре. Сложной не столько по содержанию (с этим дети справятся быстро), сколько в коммуникативном плане: при обнаружении повторяющейся буквы чью букву оставить, а чью убрать.

Повторить расположение букв в алфавитном порядке обязательно следует перед началом выполнения проекта по сортировке массивов слов. Объем и количество упражнений, связанных с повторением, зависят от подготовленности класса и желания учителя. Эту деятельность можно либо оформить как мини-проект в один-два урока, либо разбить на серию упражнений и включать фрагментами в различные по тематике уроки.

Еще раз необходимо подчеркнуть, что автоматизированный навык построения алфавитной цепочки поможет в дальнейшем успешному осуществлению проекта.

Основной проект

Разобьем наш большой проект «Сортировка слиянием» на шесть более мелких мини-проектов, каждый из которых имеет свою содержательную цель. Эти мини-проекты выстроены в цепочку, каждый последующий элемент в ней продолжает предыдущий. Их обязательно надо выполнять по порядку. Правильнее считать все мини-проекты частями одного большого проекта. Мы выделяем их, так как каждый из них, являясь частью целого, имеет и свою законченную цель.

Мини-проект 1: найти слово, которое идет раньше всех из небольшого массива слов. Выполнять этот мини-проект лучше всего в небольших группах по 2 – 4 человека. Возьмите один комплект карточек (16 листов по 24 карточки). Раздайте каждой группе по одному листу с карточками (24 слова), лучше предварительно разрезав его на карточки. Каждую группу попросите из своих слов найти первое слово – слово, идущее раньше всех других. В процессе поиска учащиеся должны постараться объяснить друг другу, как и что они делают. Им надо ответить на два вопроса:

1. Как они нашли это слово?
2. Почему они уверены, что это слово первое?

Чтобы быть уверенным, что выбранное слово первое, надо сравнить его с каждым из остальных в своей кучке слов и убедиться, что оно идет раньше всех. Самым простым способом действия (при условии, что заняты один или несколько человек, которые не разделяют работу между собой) будет следующий:

1. Взять два первых попавшихся слова.
2. Из них выбрать то, которое стоит раньше, а второе отложить в сторону.
3. Выбрать из кучки карточек новое слово вместо отложенного и вернуться ко второму пункту алгоритма – снова выбрать первое из двух, а ненужное отложить.
4. Когда в исходной кучке карточек не останется слов, у нас в руках будет самое первое слово.

Дети могут предложить много различных способов действия, и необходимо только отследить их правильность – выбранное слово надо обязательно сравнить (прямо или косвенно) со всеми остальными. На этом этапе особенно важно, чтобы дети проговаривали то, что они делают.

Мини-проект 2: найти слово, идущее раньше всех из нескольких массивов слов. Этот проект очень короткий, но его выполнение и последующее обсуждение имеют большое значение для понимания оптимального, наиболее быстро приводящего к достижению результата алгоритма слияния нескольких массивов слов. После завершения мини-проекта 1 обычно кто-то довольно быстро догадывается, что первое из всех слов надо искать среди первых слов каждой группы. Поскольку таких слов немного, то нужное слово увидеть нетрудно – так же как в мини-проекте 1, даже еще быстрее. Но стоит проговорить еще раз необходимость сравнения выбранного слова со всеми остальными первыми словами из групп и косвенного (по транзитивности) сравнения со всеми 384 словами.

Можно предложить такой порядок действий:

1. Все группы поднимают свое первое слово на всеобщее обозрение. Теперь каждая группа имеет возможность сравнить свое первое слово с первыми словами остальных групп.
2. Далее все, считающие, что их слово не первое, опускают его. Через некоторое время поднятым останется одно слово, которое и будет самым первым среди всех. Дети могут ошибаться, поэтому надо попросить каждого опускающего слово объяснить, почему он это делает. Например: «У нас слово ворота, а у Саши – барабан. Слово барабан стоит раньше, чем ворота, значит, мы можем опустить свое слово». Не сразу все понимают, что они могут опустить свое слово, если увидели хотя бы одно слово, которое стоит раньше него.

Стоит задать вопрос и о том, как можно найти второе слово. Эта задача значительно более трудная для понимания. Скорее всего, дети предложат искать второе слово среди оставшихся первых слов. На самом деле выбранное таким способом слово совсем не обязательно будет вторым из всех слов. Постарайтесь при раздаче карточек группам предусмотреть, чтобы первые два слова оказались у одной группы (это необходимо сделать для того, чтобы дети смогли понять, как происходит поиск второго, третьего слова и т. д.).

Несколько слов о параллельной организации работы

В первой части проекта учащиеся научились находить первое слово из 24 слов. Это задача, скорее всего, не была для них сложной. Обсуждая правила нахождения первого слова, мы выяснили, что при самом быстром способе нахождения для 24 слов необходимо сделать 23 сравнения. Если на каждое сравнение уходило приблизительно 20 секунд, то на отыскание первого слова у группы ушло чуть менее 8 минут (на практике в такое время укладываются все группы; столько же времени потребовалось бы и одному человеку).

Теперь подумаем, сколько времени израсходует один человек на нахождение первого из 384 слов (при применении такого же алгоритма понадобится уже 383 сравнения). Если бы на каждое сравнение уходило опять 20 секунд, то вся работа заняла бы уже

383 × 20 : 60 ≈ 128 минут (2 часа 8 минут).

Причем совершенно неважно, работает по этому алгоритму один человек или сразу весь класс, – дело будет продвигаться одинаково медленно. А нам вместе с детьми в первом и втором мини-проектах удалось найти первое слово из 384 гораздо быстрее. Почему? Давайте обсудим это с ними.

У детей появятся различные версии. Важно выделить главную: на первом этапе проекта все группы работали одновременно и каждая группа делала свою часть работы параллельно с другими. Во второй части мини-проекта учащиеся для выполнения общей задачи использовали результаты работы групп. На первый мини-проект ушло около 8 минут, на второй – еще около 8 минут. Время значительно отличается от 2 часов 8 минут!

Если удастся разделить работу на части и каждую из частей поручить отдельной группе, то выигрыш во времени при ее выполнении будет значительным. Правда, это достигается только в том случае, если группы работают одновременно. Действительно, если 384 слова разделить на 12 групп, то каждой достанется 32 слова и потребуется сделать 31 сравнение (всего 31 × 12 = 372), а затем для поиска первого слова из 12 первых всему классу придется выполнить еще 11 сравнений. В сумме получаются все те же 383 сравнения. Если бы группы работали друг за другом, то времени понадобилось бы больше трех уроков. Но группы действовали одновременно, и можно считать, что времени было затрачено всего на 33 + 11 = 34 сравнения – чуть больше 11 минут. Таким образом удалось значительно сэкономить время, правда, в данном случае за счет увеличения числа работников (ресурсов). Реально из-за временных затрат на объяснения и обсуждения мини-проекты оказываются, конечно, более продолжительными.

Интересно измерить чистое время, необходимое для выполнения работы. Засекать начальный момент следует всегда после окончания объяснений и обсуждений по команде «начали». Хорошо, если в классе будут большие часы с секундной стрелкой или спортивный секундомер (лучше иметь и то и другое).

Мини-проект 3: сортировка слов в небольших группах. Теперь попросим каждую группу упорядочить все свои 24 слова.

Можно вначале обсудить, какие варианты организации работы существуют, но лучше просто предложить упорядочить слова и понаблюдать, как каждая группа будет это делать. Если какая-то группа справилась со своей работой быстрее, можно попросить этих ребят помочь другой, лучше всего самой медлительной группе. Помогать можно по-разному, но разумнее всего порекомендовать взять у отстающей группы несколько слов и разместить их в своей упорядоченной цепочке.

После того как все мешки слов будут превращены в цепочки расставленных в алфавитном порядке слов, попросите детей каждой группы рассказать о том, как они это делали. Не исключено, что какая-то группа действовала неправильно; в таком случае будет хорошо, если другие дети заметят это. Можно предварительно попросить группы проверить правильность расстановки слов одна у другой.

Скорее всего, учащиеся не станут делить свою работу в группах на части, а просто будут действовать вместе, как делал бы это один человек, только контролируя друг друга. Часто получается так, что по существу все выполняет один – лидер, а другие лишь помогают ему двигать карточки. Впрочем, здесь самоорганизация детей обычно не отличается от организации любой другой групповой деятельности.

В этом проекте для нас важнее не организация взаимодействия в группе, а те правила, по которым упорядочиваются слова. Детям, которые быстро и правильно справились с задачей, бывает трудно рассказать о том, как они это сделали.

Обсуждая результаты, полученные группами, надо отличать неправильно выполненную работу (в результате которой слова были неправильно упорядочены) от нерациональной (порядок слов оказался правильным, но выполнялось много лишних действий). Не стоит оценивать, кто работал рациональней: детям понять это будет пока трудно, даже если учителю все ясно. Важно, чтобы дети проговаривали свои действия.

Мини-проект 4: слияние упорядоченных массивов. Теперь настало время объединить работу групп и создать один  упорядоченный массив слов.

После постановки задачи надо обсудить с детьми их предложения по дальнейшей организации работы. Учащиеся обычно сразу отметают предложение все опять смешать и начать заново. Всегда побеждает идея воспользоваться уже наведенным порядком. Дети вспоминают второй мини-проект, когда при поиске первого слова использовался результат, полученный группами.

Сначала предложим детям объединить только две цепочки слов. Правильным будет такой порядок действий, который позволит сливать два упорядоченных массива, сразу создавая порядок.

Например, так. Перед учениками лежат две упорядоченные стопки карточек, причем сверху находятся те, что идут в словаре раньше. Сравниваем две верхние карточки в стопках и первую из них (в словарном порядке) кладем в третью (вновь созданную) словом вниз.

Дальше сравниваем оставшиеся верхние карточки и снова первую из них кладем в третью стопку на первую карточку словом вниз. И так продолжаем до тех пор, пока все карточки не будут переложены в новую стопку.

Например, пусть у нас есть две упорядоченные стопки, каждая из четырех слов. Вот последовательность действий:

Этот способ должен появиться при обсуждении у доски порядка слияния цепочек двух групп. Тут не следует торопиться, надо фиксировать и обсуждать все выполняемые шаги. Желательно, чтобы каждый шаг возникал как результат обсуждения предложений учащихся.

После того как всем станет понятна последовательность действий, предложите группам объединиться по две и слить свои цепочки. Учителю необходимо внимательно следить за организацией работы и в случае нарушения правил слияния вмешиваться. В отличие от предыдущих мини-проектов здесь нам важно усвоение выработанного способа слияния цепочек. Отклонений от правил слияния бывает меньше, если слова у каждой группы лежат не рядом друг с другом, а одно поверх другого, в стопке, карточка на карточке. Очень существенно, чтобы у детей сформировалось (пусть не сразу) понимание того, что при слиянии достаточно видеть только первое слово в стопке и быть уверенными, что все слова в этой стопке упорядочены. Нет необходимости заглядывать в остальные слова. Такая работа будет выполнена довольно быстро, и число цепочек слов уменьшится в два раза, но эти цепочки окажутся в два раза длиннее.

Как продолжить работу дальше, детям обычно бывает понятно. Надо объединять новые цепочки в еще более длинные. Замешательство обычно возникает тогда, когда число групп становится нечетным. В этом случае возможны два варианта. В первом варианте одна группа дожидается следующего этапа слияния, а во втором – одновременно сливаются слова сразу трех групп. Второй вариант является более сложным, и его можно предложить при наличии в этих группах сильных учащихся.

Нужно выполнить еще несколько этапов и последовательно слить все стопки слов в одну. Основная проблема – постепенное увеличение числа незадействованных в работе учеников по мере уменьшения числа групп. А сливать две цепочки по приведенному в этом мини-проекте правилу может и один человек. Удобно это делать и вдвоем, но больше людей не нужно.

Необходимо придумать, чем в это время будут заниматься остальные. Иначе в конце проекта получится, что «один с сошкой, а семеро с ложкой». На последнем этапе особенно много времени потребуется для слияния всех слов в единую цепочку. К тому же на этом этапе окажется больше всего не участвующих в работе детей. Поручите последнее слияние выполнить одному ученику у доски под контролем всего класса.

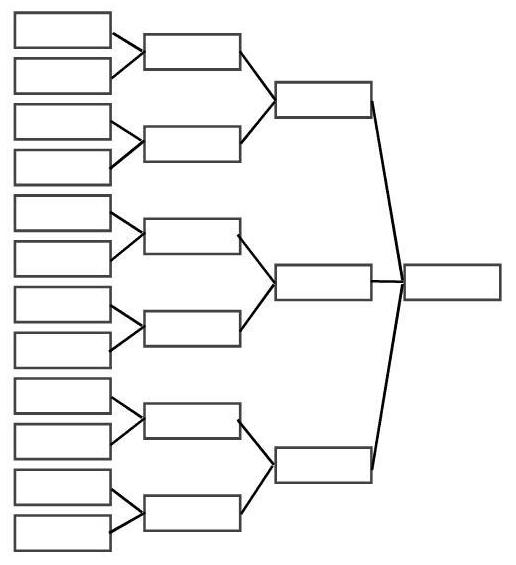
Проделанную работу надо зарисовать в виде дерева слияний (см. рисунок). Ваше дерево будет отличаться от приведенного на рисунке, его вид зависит от количества стопок слов на первом этапе сортировки.

Еще несколько слов о параллельной работе

Способ слияния двух упорядоченных массивов информации очень важен. Учащиеся осваивают его в ходе практической деятельности. Можно обсудить, сколько времени потребовалось бы одному человеку для того, чтобы упорядочить все 384 слова. Мы уже определили, что для нахождения только одного первого слова может понадобиться больше трех уроков; значит, на упорядочение всех слов, если второе и все остальные слова искать по тем же правилам, что и первое, уйдет больше учебной четверти. Нам же удалось методом слияния упорядоченных массивов и с использованием параллельной работы групп выполнить задачу гораздо быстрее. При поиске первого слова выигрыш во времени получался только благодаря параллельной работе многих учащихся. Попросите детей подумать, что происходит в случае упорядочения. Получится ли быстрее, если один человек будет упорядочивать не сразу все 384 слова, а попытается в одиночку повторить способ работы, объединяющий третий и четвертый мини-проекты. Попробуйте сами ответить на этот вопрос.

Предложите учащимся провести эксперимент. Пусть один ученик упорядочивает 24 слова, находя сначала первое слово, затем второе, затем третье и т. д., а другой, разбив их на четыре кучки, упорядочивает каждую кучку, а затем сливает полученные цепочки слов по уже выработанным в проекте правилам. Интересно сравнить время выполнения работы и занести результаты в таблицу. Затем стоит поменяться стратегиями и заполнить таблицу еще раз. 

В силу разных случайностей у каждого конкретного ученика могут иногда получиться и результаты, не соответствующие эффективности выбранного способа сортировки, но в большинстве случаев все должно быть правильно. Суммарное время будет больше при использовании первого способа.

Важно понять в процессе работы, что ускорение происходит не только за счет правильного объединения усилий большого коллектива, но и благодаря выбору эффективного алгоритма. Даже если будет работать один человек (одна вычислительная машина), сортировка слиянием (разбиение мешка на части с последующей сортировкой и слиянием упорядоченных частей) окажется самой быстрой.

Мини-проект 5: сортировочное дерево. В предыдущем мини-проекте дети научились сливать упорядоченные массивы. Мы справились с задачей довольно быстро, но от этапа к этапу оставалось все больше не участвующих в деле детей. Попробуем поставить дело так, чтобы возможности каждого в сортировке использовались наиболее эффективно. Дети уже при выполнении четвертого мини-проекта могли заметить, что для продолжения слияния более длинных цепочек необязательно дожидаться окончания слияния ее более коротких составных частей. Ведь слияние мы начинаем сверху, и к нему можно приступать, даже если работа «внизу» еще не завершена. Давайте для решения задачи упорядочения всего мешка слов организуем деятельность так, чтобы каждый ученик выполнял свою часть задачи.

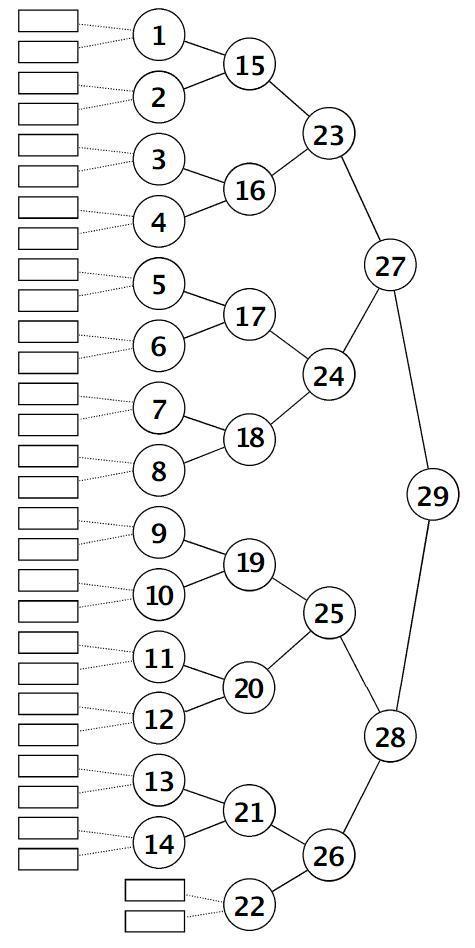
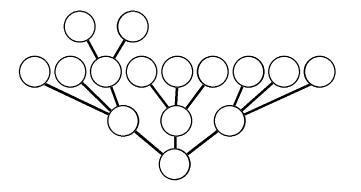
Попробуем нарисовать дерево слияний. Каждый ученик может сливать два массива, поэтому у каждой вершины (кроме листьев, конечно) будут ровно две следующие. Листьями этого дерева будут стопки слов. Число всех остальных вершин в этом дереве должно равняться числу учеников. Для 29 учеников дерево приведено на рисунке.

Каждая круглая бусина обозначает одного ученика, поэтому можно их подписать или пронумеровать (как это сделано на нашем дереве), а рядом записать, какой ученик относится к какому номеру. Следует обсудить, на чью долю в этой схеме выпадает больше всего работы. Исходя из опыта предыдущего мини-проекта, дети сообразят, что основная часть работы достанется тому, кто стоит в корне дерева. Поэтому лучше, если это будет наиболее сильный ученик, а возможно, и сам учитель.

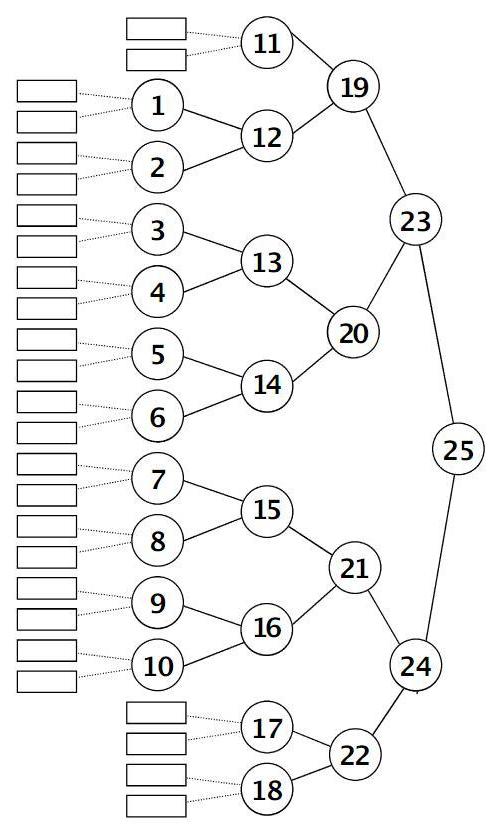
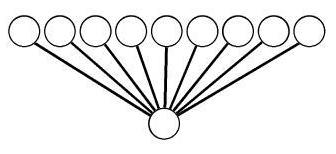
Приведенное дерево достаточно просто перестроить для любого нечетного числа учеников от 15 до 31. Для 31 ученика можно добавить две вершины на пятый уровень так, чтобы нижняя ветка дерева стала точно такой же, как верхняя. Если учеников в классе больше 31, то можно оставшихся детей назначить контролерами на разные уровни. Они будут следить за правильным выполнением алгоритма. Кроме того, «корневому» ученику возможно просто понадобится помощь. Чтобы построить дерево для нечетного числа учеников, меньшего чем 29, можно убирать с пятого уровня по две вершины, следующие за некоторой вершиной четвертого уровня, до тех пор, пока нужное число вершин не будет достигнуто. При этом следующие за убранными вершинами-учениками вершины-стопки, конечно, тоже убираются, а затем за каждой вновь появившейся вершиной-листом четвертого уровня ставим по две вершины-стопки. Например, дерево для 25 учащихся приведено на следующем рисунке.

Если в классе число учеников четное, можете либо сами поучаствовать в сортировочном дереве, либо одного ученика направить помощником к «корневому». 

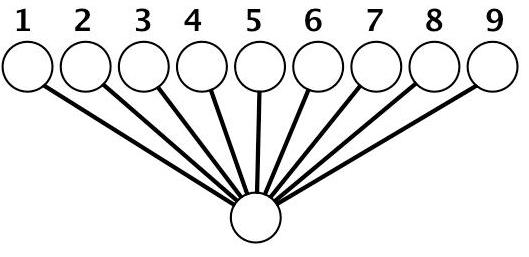
На первом этапе разобьем все слова на кучки по числу участвующих в мини-проекте учеников и попросим всех упорядочить свои слова в словарном порядке. Слов у каждого ученика будет немного, и такая задача не должна вызвать у учащихся затруднения – она знакома всем. Чтобы каждый ученик сливал ровно два массива, число стопок должно быть четным. Поэтому если число учащихся в классе нечетное, то стопок следует заготовить на одну больше. Одну дополнительную кучку может упорядочить учитель.

Теперь надо придумать, как организовать работу. Возможен следующий вариант.

На столах выложены в ряд все упорядоченные массивы. Перед ними встает в два раза меньшее (чем число массивов) число учащихся. Далее учащиеся выстраиваются в соответствии с сортировочным деревом для вашего класса. Правила взаимодействия могут быть различными.

1. Каждый ученик занимается слиянием двух массивов (массива у левой руки и массива у правой руки), но складывает карточки со словами в стопку только «корневой» ученик, а остальные отдают первую из своих двух карточек ученику, стоящему у них за спиной, причем только после того, как этот ученик попросит (например, прикоснувшись к плечу).
2. У ученика в руках две карточки. Он выбирает из них первую и отдает ее ученику, который стоит у него за спиной. Если первой была карточка в левой руке, то новую карточку надо попросить у ученика, который стоит слева (для ученика из первого ряда – взять карточку из левой кучки), а в противном случае – у ученика, который стоит справа.

Ускорение упорядочения происходит за счет параллельности работы. Хотя при такой схеме, как мы уже выяснили с детьми, не все одинаково загружены работой, эффективность может быть очень высокой. Если «корневой» ученик (или учитель) работает быстро, а дети хорошо читают или быстро узнают слова, то процесс сортировки 384 слов потребует 15 – 25 минут. После окончания сортировки нужно еще раз обсудить, кто больше был загружен и во сколько раз. Можно подсчитать, сколько сравнений сделал каждый ученик.

Алгоритм, описанный в данном мини-проекте, называется «алгоритмом пузырькового всплытия».

Мини-проект 6: сортировка через классификацию. Мини-проект дает третий алгоритм выполнения той же задачи – сортировки большого массива слов (16 × 24 слов) силами всего класса.

1. Разделите все карточки поровну на всех учащихся и попросите рассортировать их по мешкам (коробочкам, столам) так, чтобы в каждом мешке оказались слова на одну букву. При этом мы предварительно распределяем столы под мешки и подписываем эти столы с помощью большой таблички с буквой. Раскладывать слова могут все одновременно, перемещаясь по классу.
2. Затем каждый ученик садится за один стол (или берет один ящик) со словами на определенную букву и наводит порядок в данных карточках. О том, кому какая буква достанется, вам надо подумать заранее. Количество слов в наборе на разные буквы различно. Есть очень «популярные» буквы, слов на которые больше 20 (В, К, Л, М, Н, П, С, Т). Ящики с такими буквами лучше поручить сильным учащимся. Есть буквы, на которые в наборе слов меньше 10 (А, Г, Е, Ё, З, И, Ф, Х, Ц, Э, Ю, Я). В соответствующих этим буквам ящиках смогут разобраться даже слабые и медлительные дети. При этом кому-то из ребят придется заниматься сразу двумя ящиками. Все эти детали лучше продумать при подготовке к уроку.
3. Работы всех учеников собираются в алфавитном порядке первых букв. Обсудите с учениками, как проходила работа, и спросите, как они думают – всегда ли будет получаться так удачно? Они должны понять, что такой способ хорош лишь в определенных случаях. Продемонстрируйте это, предложив массив слов, у которых первые 2 – 3 буквы будут одинаковыми. В этом случае придется по ходу действия менять алгоритм работы. Хорошо, если в результате последующих обсуждений дети усвоят, что данный алгоритм сортировки не универсальный (эффективность алгоритма зависит от конкретного набора слов), в отличие от универсального алгоритма сортировки слиянием упорядоченных массивов (эффективность не зависит от конкретного набора слов).
4. Стоит обсудить, нужны ли не универсальные алгоритмы. Если не возникнет никаких побочных проблем (например, неудобно стоящие столы), то при «хорошем» наборе слов (на каждую букву слов приблизительно одинаково) задача сортировки массива с помощью алгоритма упорядочения через классификацию будет выполнена значительно быстрее, чем посредством алгоритма пузырькового всплытия.
 
5. Важно обговорить роль каждого человека – маленького процессора, и координатора их работы – главного процессора (учителя или сильного ученика).

Список всех слов (в словарном порядке)

Дополнительные мини-проекты: сортировка без обязательного упорядочения

Часть 1. Сортировка большого количества объектов, различающихся по одному признаку. Часто в жизни приходится раскладывать по коробочкам и ящичкам какие-то предметы (по тем или иным обстоятельствам сваленные в одну общую кучу) так, чтобы в каждом ящичке оказались только одинаковые.

Например, в шкафу на кухне порвались два пакета с крупой – один с гречкой, другой с рисом. Когда крупу собрали с полки, получился один мешок, в котором смешаны рис и гречка. Теперь надо рассортировать этот мешок. Одному человеку это сделать сложно. Даже Золушка смогла быстро выполнить порученную ей работу только с помощью большого числа ловких помощников. Попробуем решить задачу сортировки в классе. Задача на всех одна, поэтому надо найти способ объединить усилия. Собраться всем вокруг одного мешка и начать раскладывать крупу в два других мешка очень неудобно. 30 человек начнут просто толкаться, и дело будет продвигаться медленно. Давайте попробуем распределить работу между всеми учащимися в классе равномерно. Для этого разделим мешок смеси на маленькие кучки по числу детей в классе и попросим заняться сортировкой своей маленькой кучки каждого ученика самостоятельно. В этом случае каждый работает в своем собственном темпе и ему никто не мешает. Если кто-то успел выполнить сортировку своей кучки быстрее других, он может помочь товарищам, забрав у них часть смеси.

Дальше все просто. Надо лишь объединить все кучки с рисом в один мешок, а все кучки с гречкой в другой. Работа будет выполнена очень быстро. Затем следует обсудить, почему всем классом удалось рассортировать рис и гречку так быстро: 30 человек должны справиться с задачей в 30 раз быстрее, чем 1 человек, если они будут работать одновременно.

В данном случае разделение задачи на подзадачи принесло нам выигрыш во времени только потому, что все подзадачи выполнялись одновременно разными исполнителями. На самом деле во многих случаях и один человек будет выполнять задачу быстрее, если правильно разделит ее на подзадачи. Мы убедились в этом при рассмотрении проекта сортировки слов методом слияния.

Необязательно сортировать такие мелкие предметы, как рис и гречка. Можно взять любые объекты: горох и фасоль, пуговицы, винты и гайки из железного конструктора и т. д. Хорошо, если удастся найти что-то такое, что действительно надо рассортировать для дальнейшего использования в классе. Главное, чтобы куча объектов была достаточно большой, а различных типов объектов в ней было не больше четырех.

В сортировке надо выделить два случая: а) количество типов разных бусин заранее известно; б) количество типов бусин заранее неизвестно.

Часть 2. Сортировка большого количества объектов, различающихся по нескольким признакам. Для сортировки подойдут детали ЛЕГО, бусины из учебника или что-то подобное. Главное, чтобы различных типов объектов было немного (до 10), а самих объектов было достаточно много.

Предложите детям в небольших группах рассортировать все объекты, придумав самостоятельно, как это сделать. У детей обычно появляется два способа.

1. Сначала объекты группируются по одному признаку, затем каждую группу делят на части по другому признаку:

1. Каждому новому виду объектов сразу отводится новый мешок. Сортировка производится в один этап:

Обсудите с учащимися преимущества первого способа (легче разделить задачу на части, на каждом этапе появляется небольшое число групп).

Если предварительно известно, какие мешки надо завести, то сортировка по второму способу тоже будет не сложной. Хотя дети, скорее всего, все равно будут размещать квадраты с одной стороны, а треугольники с другой. Так проще.

Обсуждая второй вариант классификации, необходимо заострить внимание на основной проблеме: если неизвестно, сколько всего типов предметов существует (мешки заранее не приготовлены), то надо знать, есть ли уже для каждого очередного предмета мешок (такой же предмет уже был) или надо заводить новый. Если мешков мало, то можно обойтись без всякой системы, но с увеличением их числа при отсутствии системы сложно быть уверенным, что в разных углах комнаты не лежат совершенно одинаковые кубики.

Часть 3. Сортировка большого числа разнородных объектов. Для сортировки лучше всего подойдут детали ЛЕГО из различных наборов, особенно технологических. Если таких или других подходящих объектов нет, то можно специально для проекта изготовить набор плоских картонных фигурок разных форм и цветов или воспользоваться рисунками лиц людей (например, несколькими копиями соответствующей задачи из учебника для третьего класса). Главное, чтобы различных типов объектов было много (не меньше 50) и каждый объект встречался несколько раз.

В процессе работы учащиеся довольно быстро придут к выводу, что во избежание ошибок необходимо навести в процессе сортировки определенный порядок: выстроить мешки в цепочку и каждую новую бусину (или любой другой объект) проводить по этой цепочке. Если при продвижении по цепочке не удастся найти подходящий мешок для очередной бусины, то ее надо будет положить в конце цепочки, тем самым заведя новый мешок. На рисунке дерева сортировки ветки дерева можно обходить слева направо, ища подходящую ветку (см. рисунок). Каждая бусина дерева сортировки – мешок с определенным критерием.

Заключение

Умение сортировать (группировать и упорядочивать) различные массивы информации очень важно. Поэтому сортировке следует уделить достаточно много времени, благо материал для этого в школе всегда под рукой.

Вот несколько примеров:

• книги (сортируются по различным признакам: по авторам, по названиям, по темам, по жанрам, по наличию/отсутствию иллюстраций);
• детали различных конструкторов;
• карточки с названиями городов и числами (сортируются, например, по дате основания города, по числу жителей и т. п.);
• карточки с названиями стран и их столиц (можно сортировать по алфавитному порядку стран или столиц либо раскладывать по материкам и частям света).

Богатые возможности предоставляют карточки с фамилиями учеников, раскладываемые по адресам: большие мешки – улицы, мешки поменьше – дома; следующие уровни – подъезд, этаж, квартира. Можно нарисовать дерево сортировки.

Предложите детям построиться по дням рождения в календарном порядке, чтобы найти самого старшего в группе или самого младшего (для этого у каждого ребенка должна быть заготовка в виде небольшого плакатика с датой рождения – год, месяц, день):

– сначала дети выясняют, одного ли они года рождения;– если год совпадает, то смотрят на месяц и выстраиваются в порядке возрастания;– в группе одного года и одного месяца дети разбираются с днями рождения и снова строятся в порядке возрастания.