Информатика. 3 класс Демо+методичка

Уроки 23–24. Робик. Конструкция повторения

Важнейшим моментом в формировании человеческого мышления, языка, деятельности было выделение в окружающем мире и самом себе отдельных объектов, событий и действий и присвоение им имен. Объекты, предметы оказываются расположенными в пространстве, события и действия – во времени. В частности, возникает представление о событиях, следующих одно за другим, и о причинно-следственной связи. То же происходит и в процессе развития ребенка.

Циклическое повторение событий или действий является одним из основных образцов, выделяемых человеком в окружающем мире и своей деятельности. Природа задает цикличность событий, человек, подчиняясь событийным циклам, циклично организует свои действия. Цикличность стала основой измерения времени, музыки, многих ритуалов и игр, организации производственных процессов.

В попытке выделить основные модели организации алгоритмических процессов, выполняемых по определенным правилам человеком или машиной, люди (прежде всего математики) также выделили определенные, часто встречающиеся образцы. Среди них имеется и цикл.

Решение задач из учебника

Задача 139. Ученики впервые встречаются с конструкцией повторения, поэтому необходимо проследить, все ли правильно понимают ее смысл. Например, стоит обсудить, зачем в конструкции нужно слово КОНЕЦ или зачем конструкция заключена в отдельную оболочку. Если у ребят возникнет затруднение, попросите записать программу Т без оболочек и слова КОНЕЦ и поинтересуйтесь, какие команды будет повторять Робик и сколько раз: Робик повторит все команды, следующие за строкой ПОВТОРИТЬ 4 РАЗА, и результат выполнения программы будет совершенно иным, нежели при выполнении исходной программы Т. Слово КОНЕЦ указывает, что команды, которые нужно повторять, закончились. Заключение конструкции в отдельную оболочку-бусину, с одной стороны, подчеркивает целостность операции повторения (от слов ПОВТОРИТЬ ... РАЗ до слова КОНЕЦ). С другой стороны, такая оболочка оставляет программу, содержащую конструкцию повторения, по-прежнему цепочкой – на этот раз бусинами цепочки являются как отдельные команды, так и целые конструкции. Выделение служебных слов конструкции (ПОВТОРИТЬ, КОНЕЦ) другим шрифтом несет важную смысловую нагрузку. Цель – отделить эти служебные слова от собственно команд исполнителя. Все эти вопросы необязательно сразу обсуждать со всем классом. Возможно, кто-то из самых любопытных учеников задаст вопросы – вам нужно быть к ним готовым.

Ученикам, которые запутались, предложите обводить на поле повторяющиеся рисунки, получаемые при выполнении конструкции повторения: так будет несложно проверить, во-первых, что они получаются одинаковыми, а во-вторых, что их получилось именно 4.

Ответ:

Задача 140. Чтобы избежать ошибок при выполнении программы с конструкцией повторения, можно не только обводить повторяющиеся рисунки на поле. Можно ставить пометки и в программе: например, ставить галочку около слова КОНЕЦ в тот момент, когда очередное выполнение внутренних команд цикла закончено. Как только галочек станет столько, сколько указано после слова ПОВТОРИТЬ, выполнение этой конструкции повторения нужно закончить.

Ответ:

Задача 141. Дети начинают учиться писать программы с новой конструкцией. В этой задаче они опираются на готовую структуру и лишь вписывают команды в окна, но и этого вполне достаточно, чтобы почувствовать себя соавторами программы О. Результаты выполнения программы будут совершенно разными, в зависимости от того, какие именно команды впишет учащийся. Размеры поля позволяют выполнить любую из возможных программ. Однако такая свобода для ребенка будет сильно осложнять вам этап проверки. Можно попробовать осуществить парную проверку, когда после окончания решения ученики меняются решениями и выполняют программы друг друга на запасном поле со вкладыша тетради проектов, а потом сопоставляют результаты.

Задача 142. Чтобы быстро и аккуратно просматривать слова в столбике и фиксировать наличие в них двух одинаковых букв, нужно придумать какой-то способ. Например, помогут пометки: можно ставить точку около уже просмотренного слова и даже отмечать в нем две одинаковые буквы. Некоторая логическая тонкость может состоять в том, чтобы прекращать просмотр столбца, как только в нем найдется слово, в котором нет двух одинаковых букв.

Слова, находящиеся в мешках, знакомы детям, но кто-то может не знать или неправильно понимать значения слов «фуфайка», «деверь», «касторка». Хорошо бы найти непонятные слова в словаре и вообще приучить ребят не пропускать в речи или тексте непонятные слова.

Ответ: условию задачи удовлетворяет мешок Q.

Задача 143. В задаче впервые встречается то, что в программировании называется вложенным циклом, – мы несколько раз выполняем программу, а сама эта программа содержит участки, выполняемые по несколько раз. Надеемся, что задача не вызовет трудностей у детей, ведь они уже видели и цепочки внутри цепочки, и мешки внутри мешка, и (в математике) скобки внутри скобок.

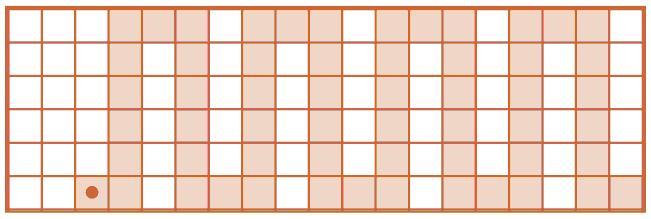
Начать решение нужно с выполнения программы Ж. Позиция после выполнения программы Ж показана на рисунке:

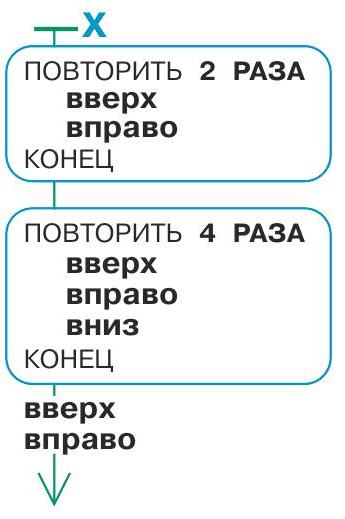
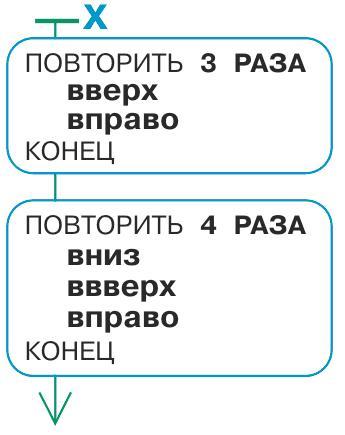
Дальнейшее решение состоит из двух этапов. Первый – убедиться с помощью рассуждений, что при выполнении программы Р Робик проходит тот же путь, что и при выполнении программы Ж. Второй – еще раз убедиться в этом, выполнив программу Р. Возможно, интереснее попросить ребят сначала выполнить программу Р, поскольку некоторым ученикам может быть скучно выполнять программу с заранее известным результатом и они отнесутся к заданию формально. Приготовьтесь к тому, что при всей простоте выполнение программы Р может вызвать вопросы из-за новой конструкции вложенного цикла. Интересно и необходимо выслушать рассуждения ребят, почему результаты выполнения программ получились одинаковыми. После того как задача решена, можно спросить ребят, какую из программ легче читать, понимать и выполнять.

Задача 144. Некоторые дети нарисуют бусины первого уровня, потом к ним присоединят заданные бусины второго уровня, а к ним приделают листья. Таким детям нужно предложить снова вернуться к условию – в дереве должно быть ровно два уровня бусин.

Если ребенок любит рассуждать, то он, скорее всего, использует следующие соображения. Так как дерево имеет два уровня, то все бусины второго уровня – листья. Однако не все листья – бусины второго уровня, значит, остальные листья – бусины первого уровня. В данном случае корневая желтая круглая бусина – лист, а синяя квадратная – не лист.

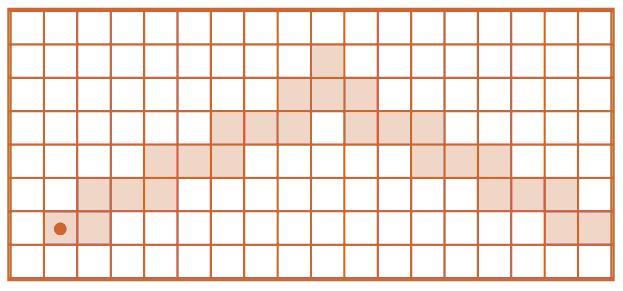
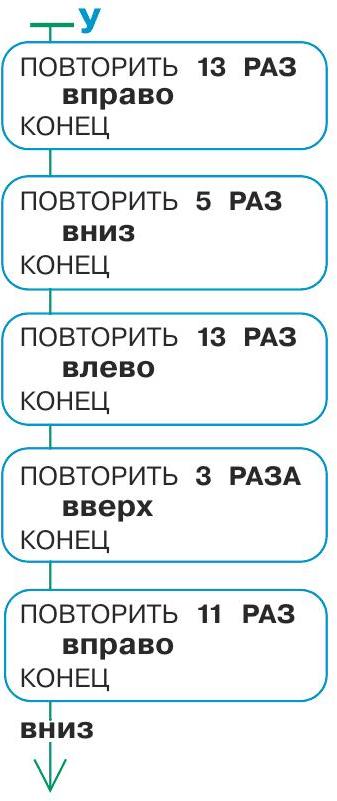
Задача 145. Заготовка для программы задает число конструкций повторения: их должно быть пять. Поскольку узор тоже состоит из пяти прямых участков, по содержанию задача не слишком сложная. Здесь важно только не сбиться и правильно подсчитать число выполнений того или иного повторяющегося участка. Для этого, во-первых, нужно правильно подсчитать число клеток на поле по вертикали и по горизонтали, а во-вторых, сообразить, что на первую клетку каждого отрезка пути Робику не надо шагать – он на ней уже стоит. Для проверки предлагается выполнить написанную программу на запасном поле и сравнить результаты. Главное, чтобы учащиеся не отнеслись к заданию формально, просто подогнав результат под данную в условии позицию.

Ответ:

Задача 146. Место для буквы В найдется быстро. Дальше ребята начнут действовать каждый по-своему. После того, как получится ответ – слово ТЕТЕРЕВ, можно спросить, что оно означает, попросите найти это слово в большом толковом словаре.

Задача 147. Эта задача на толкование слов из числа несложных. Все толкования в ней либо совпадают со словарными, либо полностью им противоречат. Поэтому данную задачу можно использовать для текущей проверки темы «Толкования слов» –  к настоящему моменту с подобными задачами должны справляться все учащиеся.

Ответ: предпоследнее и последнее утверждения истинные, а остальные – ложные.

Задача 148. В задаче требуется преобразовать программу, найдя в ней повторяющиеся участки и переписав их с использованием конструкции повторения. Кто-то может отметить, что при этом программа не стала короче, она занимает столько же, или почти столько, или даже больше места. Спросите, стала ли программа понятнее, легче ли ее читать. Постарайтесь добиться понимания того, что программа стала лучше восприниматься человеком и что такую программу проще выполнять и машине.

Дети могут по-разному выделить циклические участки. Здесь не ставится задача достичь полной оптимальности, важны лишь правильность преобразования, эквивалентность исходной программы и полученной. Например, условию удовлетворяет следующая программа:

Вопрос об оптимальности программы, пожалуй, слишком сложный, чтобы мы могли его на этом этапе обсудить со всеми детьми – дать лист определений, достичь общей договоренности. Мы можем сравнивать две программы, дающие один результат, только как цепочки – по их длине. При этом каждая конструкция повторения считается одной бусиной. Но такое сравнение похоже на сравнение программ по оптимальности только в случае, если все конструкции в них одинарные, т. е. внутри конструкции повторения нет других конструкций, как, например, в программе Р задачи 143.

В связи с этим в курсе нет заданий на создание минимальной или оптимальной программы. Вы можете попросить сильных учеников написать другую, более короткую программу. Для работы со всем классом задачу можно использовать как повод дополнительно поиграть или порассуждать с учащимися. Например, можно попросить ребят выписать все различные варианты своих программ на доске, затем выбрать экспертов (которые будут в роли Робиков) и попросить выбрать на их взгляд наиболее понятную и простую для исполнения программу. В данном случае наиболее простой, понятной и одновременно наиболее короткой будет программа, данная на следующем рисунке:

Задача 149. Задача на повторение листа определения «Склеивание цепочек», использующая русские слова. Обратите внимание, что разбиение слова здесь происходит не по правилам русской морфологии.

Задача 150. В этой задаче стоит уделить внимание первому утверждению: «Антрацит – это каменный уголь». Как видите, здесь предложено неполное толкование, дети уже встречали такие неполные толкования в задаче 134. В словаре написано: «Антрацит – лучший сорт каменного угля» (это истинное утверждение). Верно ли, что «антрацит – это каменный уголь»? Да, верно. Значит, наше утверждение тоже истинно. С определением истинности остальных утверждений ученики вполне справятся самостоятельно.

Ответ: первое, третье и пятое утверждения истинны, остальные – ложны.

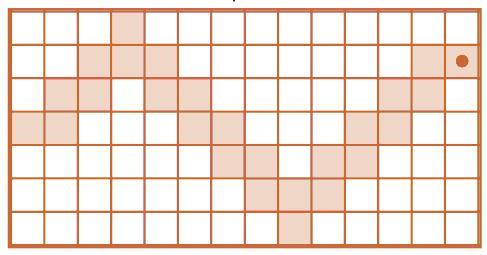
Задача 151. Необходимо выполнить программу с вложенным циклом, но в отличие от задачи 144 результат неизвестен и его нельзя предугадать. Дети должны аккуратно выполнить программу. Трудности возникнут у ребят, которые попытаются одновременно считать количество повторений внешнего и внутреннего циклов. Посоветуйте им обводить на поле рисунок после выполнения всех команд, начиная от записи ПОВТОРИТЬ 4 РАЗА и до записи КОНЕЦ. Это поможет не допустить ошибок при переходе от одной такой части к следующей. Кроме того, можно ставить пометку около слова КОНЕЦ всякий раз после выполнения всех команд, находящихся после записи ПОВТОРИТЬ 4 РАЗА и до записи КОНЕЦ. Как только наберется четыре пометки, нужно остановиться. Для быстрой проверки спросите, где теперь находится Робик.

Ответ:

Задача 152 и задача 153 (необязательная). В отличие от предыдущих подобных задач на склеивание/разрезание слов для решения этих задач необходимо использовать информацию из курса русского языка. Если в вашей школе есть возможность проведения интегрированных уроков, эту и подобные задачи (которые встречаются и дальше) можно выбрать для решения на таких уроках.

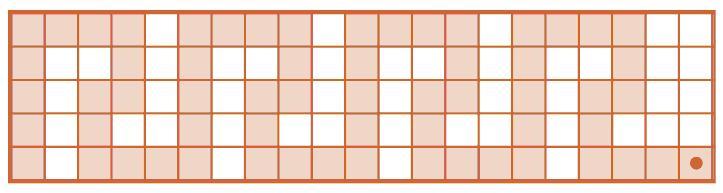
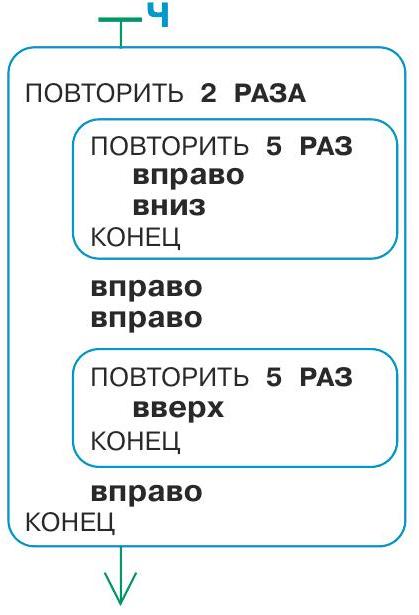
Задача 154. Эта задача напоминает задачу 145. Но здесь заготовка программы вынуждает ребенка использовать конструкцию вложенного цикла. Это означает, что рисунок, закрашенный Робиком, должен состоять из нескольких одинаковых частей (и в каждой части есть еще мини-циклы). Сначала надо выделить в узоре такие части и сосчитать их число (2). Одна такая часть – рисунок, который закрашивает Робик, выполняя внутренние команды большого (внешнего) цикла 1 раз. Осталось написать эти команды – теперь задача стала аналогична задаче 145.

Ответ:

Компьютерный урок «Робик. Конструкция повторения», 1 часть, задачи 138 - 145

Задача 138. Это первый урок, где ученики встречаются с конструкцией повторения, поэтому необходимо проследить, все ли правильно понимают её смысл. Например, стоит обсудить, зачем в конструкции нужно слово КОНЕЦ или зачем конструкция заключена в отдельную оболочку. Если у ребят возникнет затруднение, попросите записать программу А без оболочки и слова КОНЕЦ и поинтересуйтесь, какие команды будет повторять Робик и сколько раз. Слово КОНЕЦ указывает, что команды, которые нужно повторять, закончились. Заключение конструкции в отдельную оболочку-бусину, с одной стороны, подчёркивает целостность операции повторения (от слов ПОВТОРИТЬ ... РАЗ до слова КОНЕЦ). С другой стороны, такая оболочка оставляет программу, содержащую конструкцию повторения, по-прежнему цепочкой – на этот раз бусинами цепочки являются отдельные команды и конструкции повторения. Все эти вопросы необязательно сразу обсуждать со всем классом. Возможно, кто-то из самых любопытных учеников задаст вопросы – вам нужно быть к ним готовым.

Задача 139. Скорее всего, эту задачу дети будут решать методом проб и ошибок, ставя в конструкцию повторения разные числа и заставляя Робика выполнить разные программы. Впрочем, здесь возможно и решение рассуждением. Достаточно сосчитать, сколько шагов нужно пройти Робику вниз из начальной позиции до нижнего левого угла – четыре шага. Значит, ставим 4 в программу и проверяем, что Робик действительно пришёл в нужную клетку.

Задача 140. Похожие задачи, но без конструкции повторения, ребята уже решали. Поэтому, надеемся, все дети будут знать, с чего начать решение. Дети, скорее всего, будут перебирать все клетки поля, выбирая наугад. Но может быть, кто-то из детей будет готов сначала проанализировать ситуацию. При анализе программы становится ясно, что в ходе её выполнения Робику придётся подняться на 4 шага вверх. Поэтому выбирать начальную позицию для Робика имеет смысл только в последней или предпоследней строчках поля. Рассуждая аналогично, можно сделать вывод, что Робик должен начинать свой путь из крайнего левого столбца поля. Поле этого у нас осталось лишь две возможные клетки поля, одна из которых (крайняя левая в нижней строке) нам подходит.

Задача 141. Задача на повторение темы «Все пути дерева». Аналогичные задачи детям уже встречались (см. комментарий к компьютерной задаче 132). Как и в задаче 132, здесь нужно построить по мешку путей дерево с минимальным числом бусин. Для этого бусины придется экономить, то есть не ставить на один уровень несколько одинаковых бусин, если их можно заменить одной. Например, в данном случае первые бусины всех путей одинаковые – красные круглые. Кто-то из детей сделает из этого вывод, что в дереве должна быть всего одна корневая бусина – красная круглая, но это не так. Действительно, в силу наших договоренностей одна и та же бусина не может быть одновременно и листом и не листом. Здесь же мы видим, что в одном из путей мешка Т красная круглая бусина является листом, а в остальных – нет. Это означает, что на первый уровень придется поставить две одинаковые красные круглые бусины – лист и не лист. Аналогичная ситуация встречается на втором и третьем уровнях.

Задача 142. Похожие задачи ребята уже решали не раз, поэтому предоставьте им полную свободу. В крайнем случае, застопорившемуся ребенку можно предложить метод полного перебора. По ходу перебора те слова, для которых нашлась пара, нужно соединять, а те, для которых не нашлась – помечать (например, галочкой). В результате получается три искомых пары слов: ГЛАВА и ВЛАГА, КАПЛИ и ЛИПКА, РОЖКИ и ЖИРОК.

Задача 143. Задача напоминает компьютерную задачу 139, только здесь в программе пропущено не число повторений, а команда. Конечно, все 4 возможные команды можно просто перебрать и попробовать – заставить Робика выполнить такую программу. Однако и здесь могут помочь рассуждения: если из данного положения Робик должен попасть в нижний правый угол, значит, он не должен в конце концов сдвинуться по горизонтали. То есть каждый его сдвиг вправо должен «компенсироваться» обратным сдвигом влево. Значит недостающая команда в программе – «влево».

Задача 144. Аналогичные задачи на построение цепочек ребятам уже попадались. Сложность подобных задач в том, что не удается механически сложить решение из частичных решений. Например, здесь не получается сложить решения из трех кусочков вида «баклажан - … - желтый фрукт», поскольку в цепочке должно быть ровно 7 фигурок. Поэтому приходится «сращивать» частичные решения между собой. Если «срастить» два частичных решения, то у нас получается кусочек «баклажан – баклажан – желтый фрукт – желтый фрукт». Теперь третье частичное решение к этому кусочку можно просто присоединить, и в цепочке окажется как раз 7 фигурок.

Задача 145. Сначала можно сгруппировать пары бусин по второй части задания: «квадратная – зеленая» – таких пар будет две.

Теперь будем собирать цепочки для первой части задания: «круглая – любая – синяя», при этом не разъединяя пары, полученные на предыдущем этапе. В цепочке 3 круглые бусины и 3 синие бусины, значит, нам нужно собрать три части «круглая – любая – синяя». Попробуем сделать просто: поставим по круглой бусине за одну бусину перед каждой парой «квадратная – зеленая», а третью круглую бусину поставим за одну перед синей треугольной, например так:

Как видим, на простое решение бусины в цепочке не хватит – не хватает одной бусины, чтобы поставить её после третьей круглой перед синей треугольной. Значит, придется комбинировать, накладывать наши части друг на друга, поставив две круглые бусины одну за другой.

Вариант решения:

Компьютерный урок «Робик. Конструкция повторения», 2 часть, задачи 146 - 153

Задача 146. Задача, аналогичная компьютерной задаче 140, но здесь стенки на поле задают более сложную форму доступной части поля, да и программа посложнее.

Задача 147. Задача похожа на компьютерную задачу 139, но программа состоит из четырёх конструкций повторения, число повторов в которых неизвестно. Решать эту задачу простым перебором будет довольно сложно. Лучше сначала подумать, порассуждать. Например, можно сосчитать число клеток, которые Робику необходимо пройти (и закрасить) в каждой строке, и вписывать числа в окна наверняка. Конечно, это не полностью исключит ошибки (например, вычислительные), но существенно сократит процесс перебора.

Задача 148. Несложная задача, подходящая практически любому ученику. К настоящему моменту ребята должны понимать, что наличие в дереве двух путей длины 1 означает наличие двух листьев первого уровня. Таким образом, используя условие задачи, можно сначала расставить на все уровни все листья, а затем уже соединить их в дерево с помощью бусин – не листьев.

Задача 149. Для начала необходимо выделить в рисунке, который закрасил Робик, три элемента, которые соответствуют трём циклам программы. Это лесенка «вниз»-«вправо», нижний ряд поля «влево» и лесенка «вправо»-«вверх». Теперь для каждого участка осталось сосчитать число клеток и вписать числа в окна программы.

Задача 150. Усложненная задача, требующая некоторых рассуждений. Для начала необходимо внимательно прочитать условие задачи. Подобные формулировки мы с вами уже обсуждали. Здесь все пути дерева должны быть словами из словарика, но не все слова из словарика должны быть путями дерева. Поэтому в ходе решения необходимо выбрать именно те слова, которые подойдут по структуре данного дерева. Например, в нашем дереве есть путь длины два, а в словарике два подходящих слова – НА и ЩИ. Какое из них нам подойдет? Как видим, первая буква этого слова – первая буква трех слов (путей) в дереве. В словаре слов на Щ два, а на Н – три. Значит, нам подходит слово НА. Теперь размещаем в этой же ветке слова НАС и НАСТ. Аналогично, ориентируясь на число путей во второй ветке, выбираем из словаря подходящие слова на одинаковую первую букву.

Задача 151. Аналогичные задачи ребятам уже встречались. Наиболее естественный совет для большинства ребят (за исключением самых сильных) – вначале выписать числа на листок, перевести их в арабскую форму записи, упорядочить полученные числа, а затем уже упорядочивать исходные числа.

Задача 152. Необязательная. Конечно, подобную задачу можно решить перебором клеток поля, запуская Робика из каждой клетки по очереди. Однако лучше этот перебор сразу сузить, чтобы не делать слишком много напрасной работы. При анализе программы становится ясно, что Робик не может выполнить даже первые две команды из клеток левого столбца поля. Кроме того, Робик не сможет выполнить первые три команды из двух нижних строк поля. Таким образом, сразу отбрасываем довольно много вариантов, и остаётся проверить лишь 7 клеток поля. Конечно, анализ программы можно продолжать и отбросить ещё часть клеток, но и такой перебор выполнить уже вполне реально.

Задача 153. Аналогичные задачи мы в своих комментариях обычно относим к разряду комбинаторных, хотя дети к настоящему моменту обладают совсем небольшим опытом в области комбинаторики. В данном случае речь, по сути, идет о составлении упорядоченных пар, выбираемых из трех элементов. В качестве пары выбирается два цвета из трех допустимых. При этом цвета в паре могут быть и одинаковыми, в комбинаторике это называется «выбор элементов с возвращениями». Важность порядка цветов в паре объясняется просто – один цвет относится к штанишкам, а другой – к колпачку. Менять их местами нельзя – получатся разные фигурки. Сколько же существует таких пар? Каждая деталь одежды может быть раскрашена в один из трех цветов и детали могут как угодно комбинироваться между собой, значит получается 3 • 3 = 9 пар. Как видим, фигурок здесь всего 18, значит, детям придется не просто искать комбинации, но найти все возможные комбинации. Случайным перебором (как обычно делают дети) сделать это оказывается не так-то легко. Поэтому лучше предлагать эту задачу сильным и средним учащимся.