Информатика. 3 класс Демо+методичка

Урок 22. Деревья потомков

Родословные деревья в генеалогии выглядят несколько иначе, чем деревья в нашем курсе. Различают деревья предков и деревья потомков. Корневой вершиной дерева предков является самый младший из родственников, представленных в дереве, каждый следующий уровень такого дерева — это предыдущее поколение родственников. Корневой вершиной дерева потомков является старейший представитель рода, каждый следующий уровень такого дерева — это следующее поколение потомков.

В отличие от наших деревьев, в генеалогическом дереве возможны связи между вершинами одного уровня: между мужем и женой. Дети при этом (например, следующие вершины в дереве предков) являются следующими вершинами сразу для пары (мужа и жены). Кроме того, родственные связи могут быть довольно запутанными, и часто в генеалогическом дереве для некоторых вершин нельзя точно определить их уровень (к какому именно поколению этот человек принадлежит): тётка может быть младше племянника, супруги могут быть троюродными родственниками и т. п.

Поэтому для работы в нашем курсе лучше всего подходят деревья наследования власти (специальный вид деревьев потомков). В них наследование идёт по мужской линии, поэтому в таком дереве у каждой вершины имеется не более одной предыдущей вершины, что соответствует договорённостям в нашем курсе о построении деревьев.

Цель листа определений на с. 66 учебника — дать ответы на вопросы детей, которые могут возникнуть при работе с деревьями наследования власти. Так, например, кого-то из ребят может заинтересовать вопрос, почему ни в одном дереве потомков не указаны матери.

Решение задач 132 – 138 из учебника

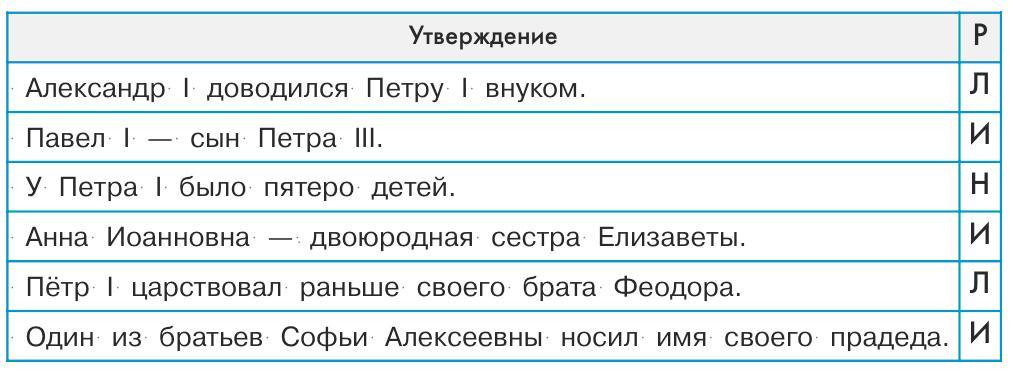
Задача 132. Поскольку дерево в задаче довольно необычное, меняется и терминология. Вершины — это потомки, следующие вершины — дети, вторая вершина перед данной — дедушка, третья вершина перед данной — прадедушка, одинаковые вершины в дереве обозначают двух потомков, названных одинаково, и т. д. Такая терминология для ребят является привычной и вполне естественной, но интересно сопоставить знакомые слова с графической иллюстрацией, со структурой дерева. Несмотря на знакомые понятия, некоторые из утверждений являются довольно затейливыми. Например, седьмое утверждение, вполне возможно, придётся обсуждать вместе — кто кому и кем приходился и кто чьё имя носил.

Ответ: второе и восьмое утверждения ложны, остальные истинны.

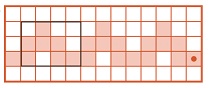
Задача 133. адача является пропедевтической (подготовительной) для восприятия темы следующего листа определений — «Робик. Конструкция повторения». Надеемся, что к настоящему моменту ребята уверенно работают даже с длинными и сложными программами для Робика. Здесь важно другое: мы обращаем внимание ребёнка на то, что получающийся в ходе выполнения программы П рисунок состоит из трёх одинаковых фрагментов. Эти фрагменты, в свою очередь, соответствуют трём одинаковым частям программы.

Решение задачи:

Задача 134. На эту задачу стоит обратить особое внимание. До настоящего момента дети встречали толкования двух типов — либо полностью совпадающие с толкованиями словаря, либо полностью им противоречащие (хотя внешне похожие). Здесь же впервые встречается неполное толкование. Речь идёт о втором и третьем утверждениях. Как видите, здесь предложено недостаточное, неполное толкование, оно содержит лишь часть информации, имеющейся в определении в словаре. Как же определить истинность такого утверждения? Например, в толковании в задаче написано, что «гонг — это ударный музыкальный инструмент». Верно ли это? Да, верно, это соответствует толкованию словаря, которое является лишь более полным, содержащим новые детали. Но эти детали не противоречат нашему толкованию, поэтому утверждение истинно. Аналогично ситуация обстоит и со вторым утверждением. Остальные утверждения ложны — они противоречат толкованиям словаря.

Задача 135. Здесь снова предстоит работа с частью дерева потомков. Надеемся, что дети оценят удобство работы с деревом: ведь на нём наглядно представлены все родственные отношения, даже самые сложные. Но, кроме вопросов о степени родства, в таблице (в этой и следующей задачах) содержатся вопросы, касающиеся дат царствования. Обратите внимание на третье утверждение: «У Петра I было пятеро детей». В условии задачи сказано, что дерево Р — часть родословного дерева, поэтому необязательно в нём должны быть все дети Петра I (так же как и всех остальных). По дереву Р можно сделать вывод о том, что у данного царя было не меньше пяти детей, но сказать что-то более определённое на основании этой части полного генеалогического дерева нельзя. Поэтому правильнее всего в соответствующей клетке таблицы поставить «Н», т. е. нам это точно неизвестно. Нужно ли обсуждать эту деталь с ребятами, решите сами, в зависимости от уровня подготовки детей в классе.

Решение задачи:

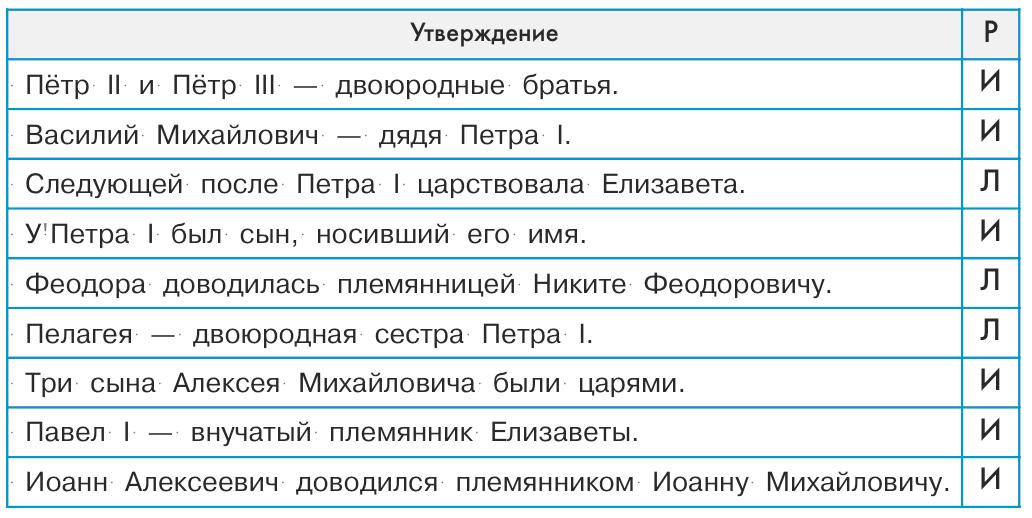
Задача 136. Необязательная. Задача несколько объёмней, чем предыдущая. Кроме привычных слов, обозначающих родственные отношения, — сын, дедушка, внук, утверждения содержат и более сложные: двоюродная сестра, племянник, внучатый племянник. Перед решением задачи следует выяснить, все ли слова в таблице понятны детям, лучше всего попросить их самих объяснить степень родства. Это может стать началом интересного разговора о том, кто знает ещё какие-либо термины, относящиеся к степени родства (тёща, невестка, шурин, деверь, сноха и др.).

Решение задачи:

Задача 137. Необязательная. Задача, аналогичная задаче 133.

Задача 138. Необязательная. Аналогичные задачи ребята уже решали (см. комментарии к задачам 82 и 121).

Ответ: ПОПОНА.

Дополнительные задачи для проекта

Материалы: лист определений, задачи 1—7 и словарь терминов родства в формате ПДФ. (Задачи 1 и 2 полностью повторяют задачи 132,135 и 136 из учебника.)

Решение задач проекта

Задача 1. Поскольку дерево в задаче довольно необычное, меняется и терминология. Вершины – это потомки, следующие вершины – дети, вторая вершина перед данной – дедушка, третья вершина перед данной – прадедушка, одинаковые вершины в дереве обозначают двух потомков, названных одинаково, и т. д. Такая терминология для ребят является привычной и вполне естественной, но интересно сопоставить знакомые слова с графической иллюстрацией, со структурой дерева. Несмотря на знакомые понятия, некоторые из утверждений являются довольно затейливыми. Например, седьмое утверждение, вполне возможно, придется обсуждать вместе – кто кому и кем приходился и кто чье имя носил.

Ответ: второе, пятое и восьмое утверждения – ложны, остальные – истинны.

Задача 2. Здесь снова предстоит работа с частью дерева потомков. Надеемся, что дети оценят удобство работы с деревом: ведь на нем наглядно представлены все родственные отношения, даже самые сложные. Но кроме вопросов о степени родства, в таблице содержатся вопросы, касающиеся дат царствования. Обратите внимание на третье утверждение – «У Петра I было пятеро детей». В условии задачи сказано, что дерево Р – часть родословного дерева, поэтому необязательно в нем должны быть все дети Петра I (так же как и всех остальных). По дереву Р можно сделать вывод о том, что у данного царя было не меньше пяти детей, но сказать что-то более определенное на основании этой части полного генеалогического дерева нельзя. Поэтому правильнее всего в соответствующей клетке таблицы поставить «Н», т. е. нам это точно неизвестно. Нужно ли обсуждать эту деталь с ребятами, решите сами, в зависимости от уровня подготовки детей в классе.

Ответ к первой части задачи:

Во второй части кроме привычных слов, обозначающих родственные отношения – сын, дедушка, внук, – утверждения содержат и более сложные: двоюродная сестра, племянник, внучатый племянник. Перед решением задачи хорошо бы выяснить, все ли слова в таблице понятны детям, лучше всего попросить их самих объяснить степень родства. Это может стать началом интересного разговора о том, кто знает еще какие-либо термины, относящиеся к степени родства (теща, невестка, шурин, деверь, сноха и др.). Если возникнут вопросы и недоумения, можно вместе обратиться к словарю терминов родства.

Ответ ко второй части задачи:

Задача 3. Если в предыдущей задаче нужно было оценить истинность предложенных утверждений, то в этой задаче нужно самим определить степень родства по предложенному дереву потомков Юрия Долгорукого.

При необходимости детям предлагается использовать словарь терминов родства.

Ответы:

1. Юрьевич.
2. Братом.
3. Отцом.
4. Племянником.
5. Внуком.
6. Правнуком.
7. Семеро.
8. Шестеро.
9. Ярослав.
10. Михаил, Святослав или Василий.
11. Дядей.
12. Племянником.
13. Даниил.
14. Двоюродными братьями.

Задача 4.  Задачи этого проекта, кроме всего прочего, помогут детям расширить свой кругозор и словарный запас. В предыдущих задачах ребята  уже встречались со степенями родства и могли проследить родственные связи по дереву. Здесь ребятам придется самостоятельно сформулировать определения, пользуясь накопленным практическим опытом. Даже тех из них, кто сразу не сможет дать точное определение, стоит попросить попытаться написать хотя бы свою гипотезу (карандашом), а уже потом заглядывать в словарь.

Задача 5. Необязательная. Определение степени родства можно сформулировать по-разному. Например, можно сказать, что прабабушка – это бабушка матери или отца, а можно –  что это мать бабушки или дедушки. Именно об этом ребятам придется задуматься в ходе решения данной задачи.

Задача 6. Необязательная. Важная задача, для решения которой может потребоваться много времени. Она помечена необязательной, потому что наверняка на нее не хватит времени на уроке проекта. Если у вас найдется возможность, возьмите час другого предмета (технологии, естествознания и пр.) и проведите второй урок по этому проекту, чтобы решить задачи 6 и 7.

Чтобы построить дерево, придется обработать большой объём информации. При этом в тексте много сведений, не нужных для решения данной задачи, однако важных для общего развития детей. Облегчает задачу лишь то, что аналогичное дерево учащиеся уже видели в задачах 1, 2 и 3. В корневой вершине дерева стоит имя Дмитрия Донского, в вершинах второго уровня – все его сыновья. Поскольку дерево должно отражать наследование власти, надо из всех сыновей Дмитрия Донского выделить наследника престола – Василия I Дмитриевича – и поместить его имя в ту вершину второго уровня, которая не является листом. На третьем уровне расположатся все сыновья Василия I. Заметим, что в тексте о Василии II наследник не указан явно. Чтобы найти среди его сыновей наследника, ребятам придется заглянуть в следующий текст. Текст о сыновьях Василия II Васильевича может вызвать вопрос у некоторых детей. Дело в том, что у князя Василия II Васильевича действительно было два сына Юрия: один умер в детстве, а потом родился другой, которого тоже назвали Юрием.

Задача 7. Необязательная. Еще одна сложная задача о степенях родства. Отец супруги Дмитрия Донского есть в дереве потомков Юрия Долгорукого. Получается, что Дмитрий Донской и его супруга Евдокия – родственники. Попросите детей найти ближайшего общего предка Дмитрия Донского и его супруги и подумать, как называется степень их родства и кем они приходятся друг другу. Ближайший общий предок Дмитрия Донского и Евдокии – Ярослав Всеволодович, который обоим приходится прапрапрадедом. Сыновья Ярослава Александр  и Андрей были родными братьями. Их сыновья Даниил и Василий были двоюродными братьями. Их сыновья Иоанн Калита и Константин были троюродными братьями. Их сыновья Иоанн Красный и Дмитрий были четвероюродными братьями. Значит, Дмитрий Донской и Евдокия были пятиюродными братом и сестрой.