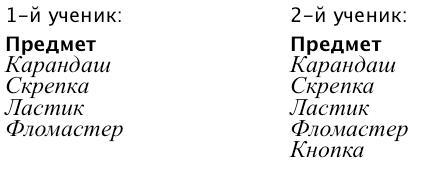Информатика. 3 класс Демо+методичка

Урок 8. Проект «Одинаковые мешки»

Перед тем как комментировать первый проект в курсе 3 класса, вспомним несколько основных положений о работе с проектами. Работа с проектом требует другой организации, чем работа с учебником. Проекты предполагают комплексную деятельность в реальном мире, не всегда полностью формализованную и опирающуюся на большой объем информации. Основная цель проектов – применение приобретенных знаний к жизненным ситуациям. Тем самым мотивируется изучение сложных вопросов информатики. Важнейшая задача проектов – показать, что информатика не только учебный предмет, но что она позволяет правильно решать многие жизненные проблемы.

В отличие от работы с учебником, почти всегда индивидуальной как на уроках, так и дома, реализация проектов включает большой объем групповой работы как на уроках, так и вне уроков, дома и на переменах. При правильной мотивации каждый проект может на некоторое время «поглотить» детей и способствовать приобретению ими важных информатических знаний в процессе совместной деятельности.

Работу над проектами можно проводить несколькими способами.

Способ 1. Погружение в материал. Урок целиком (или даже несколько уроков подряд) посвящается одному проекту. При такой организации от ребенка требуется длительное интеллектуальное напряжение, понимание объяснений и инструкций, высокий уровень заинтересованности в получении результата и во взаимодействии с другими участниками (в том числе и взрослым – организатором этой деятельности). Важно, чтобы ребенок постоянно получал естественную целостную мотивацию: «Я хочу выиграть! Я хочу успеть раньше всех! Я хочу первым узнать, что получится!»

Способ 2. Деление деятельности на фрагменты. Такой вариант предполагает дробление проекта на мелкие части с их реализацией на нескольких уроках. Каждый кусочек, «мини-проект», решает определенные задачи и подготавливает учеников к следующему этапу. Происходит многократное возвращение к материалу каждый раз на более высоком уровне сложности через определенные промежутки времени.

Мы считаем, что при работе над проектами наиболее правильным является сочетание этих двух способов. На уроке ставятся основные задачи проекта и рассматриваются простейшие случаи, формулируется задание для домашнего исследования. После нескольких подобных проектных включений и домашних исследований проводятся один или два урока-погружения в проект. При погружении без такой предварительной подготовки ребенок может не понять чего-то важного и в результате потерять интерес ко всей деятельности. В случае же организации предварительной фрагментарной деятельности вы всегда будете иметь возможность вернуться на шаг назад – так исчезнет опасность, что кто-то потеряет нить рассуждений где-то в середине пути.

Материалы к проекту: задача 1 на с. 3 – 5 Тетради проектов, вкладыши Тетради проектов: «Таблица для задачи 1» на с. XXХIХ, «Таблицы для телесных мешков» на с. XVII, «Общая таблица для телесных мешков» на с. XVIII.

Первый этап проекта

Учащиеся самостоятельно работают с задачей 1, а также участвуют в общем обсуждении того, что и как делать дальше.

Сначала ребятам предлагается придумать, как (быстрее) отыскать одинаковые мешки в задаче 1. Для этого учащиеся обычно начинают беспорядочно сравнивать пары (ведь именно так они находили одинаковые мешки в задачах учебника). Надо сразу договориться: тот, кто считает, что получил ответ, показывает его только учителю, чтобы не лишать товарищей радости самостоятельного поиска. Кто-то, выбирая пары случайно, найдет два одинаковых мешка. В этом случае надо попросить удачливого ученика проверить, нет ли еще здесь пар одинаковых мешков.

В процессе обсуждения способов сравнения мешков обязательно должен прозвучать вариант составления таблиц мешков. Действительно, сравнить две колонки чисел гораздо легче, чем два беспорядочно уложенных мешка. Каждый мешок нужно представить в виде колонки чисел – какие фигурки и в каком количестве в нем лежат. Но состав фигурок в каждом мешке свой. Можно для начала взять два мешка, скажем мешки А и С (пара А и В не годится, потому что эти мешки вообще не пересекаются), и попытаться сравнить их с помощью составления таблиц. Предложите детям подумать, как составить таблицы для мешков так, чтобы их впоследствии было удобно сравнивать. Если составлять таблицы для А и С по отдельности (дети уже делали это в задачах), то сравнивать их потом будет не намного проще, чем сами мешки. Так постепенно рождается мысль о том, что таблицы мешков должны быть «унифицированы», т. е. список и порядок фигурок для заполнения таблицы каждого мешка должны быть одинаковыми. В таком случае таблицы мешков могут быть колонками одной таблицы, и эти колонки будет легко сравнивать. Самый левый столбец в таблице (шапка) – список всех фигурок, встречающихся в мешках, а в следующих столбцах мы сможем записать, сколько каких фигурок в мешках, т. е. заполнить таблицы для мешков А и С. Если какой-то фигурки в одном из мешков нет, то в соответствующей клетке просто ставим ноль. В ходе разговора на доске появится таблица, похожая на таблицу к задаче 1, но только меньше. Левый столбец таблицы заполняется тоже в ходе просмотра мешков А и С: берем мешок А, выписываем названия всех фигурок, которые там встречаются, затем берем мешок С и дописываем ниже названия тех фигурок, которых в первом столбце таблицы еще нет (их не было в мешке А). При этом напротив этих новых названий в столбце для мешка А можно сразу проставить нули.

Главная проблема при выполнении этой работы – не записать в список дважды одну и ту же фигурку (и не назвать одну и ту же фигурку разными именами). После того как общий список готов, можно заполнить колонки (таблицы мешков) для А и С. По окончании работы учащиеся не только убеждаются в том, что мешки А и С разные, но и получают алгоритм (способ) для дальнейшей работы. Точно также можно поступить и с остальными мешками. Составив один общий список всех фигурок, которые встречаются в мешках хотя бы один раз, можно заполнить таблицу для каждого мешка и потом сравнить колонки чисел.

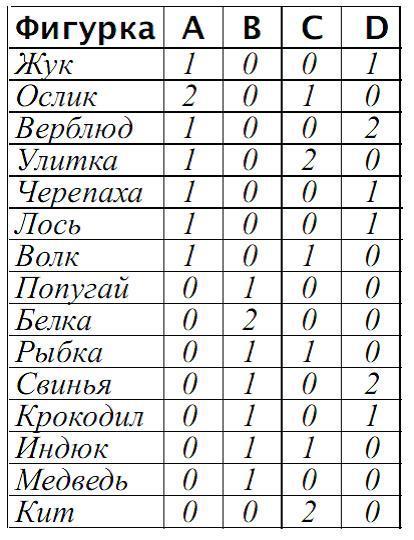
По окончании общего обсуждения каждому учащемуся предлагается самостоятельно поработать со сводной таблицей (с. XXХIХ вкладыша). В первом столбце должен содержаться общий список всех фигурок, встречающихся в мешках. Ребенок может составить его сразу целиком или по ходу просмотра мешков добавлять названия животных, которые еще не встречались. На самом деле полный список фигурок появится после просмотра первых трех мешков (А, В, С). Затем учащийся заполняет таблицу, имея в виду, что таблица каждого мешка – это колонка в сводной таблице, т. е. в столбце под именем каждого мешка.

Ниже приведен один из возможных вариантов заполнения таблицы для четырех первых мешков.

После заполнения всей таблицы (а точнее, таблиц для всех мешков) нужно найти два одинаковых столбца. Можно выявить пару одинаковых столбцов, проглядывая таблицу глазами, но лучше отсортировать таблицы мешков (мы составили мешки так, чтобы, просматривая глазами, найти два одинаковых столбца было трудно). Предложите детям следующий способ: разрезать заполненную большую таблицу на столбцы – отдельные таблицы мешков. Теперь разделим их на кучки с одинаковыми цифрами в первой строке. Затем каждую кучку делим на меньшие кучки, выбирая таблицы с одинаковыми цифрами во втором ряду, и так далее, пока не просмотрим все ряды. Постепенно число кучек будет увеличиваться, а число таблиц в кучках – уменьшаться. Кучки с одной таблицей (одиночные таблицы) можно сразу откладывать в сторону. Возвращаться к ним не придется. В результате останется одна кучка, содержащая две таблицы. Это и будут таблицы искомых одинаковых мешков.

Второй этап проекта

Для работы понадобятся настоящие мешки (например, полиэтиленовые пакетики) и телесные предметы (детали конструктора ЛЕГО или разнообразные мелкие канцелярские принадлежности). Мешки надо подготовить заранее по числу учеников, не больше 26 штук (из расчета один мешок на одного-двух учащихся), не забыв при этом изготовить ровно два одинаковых. Лучше сразу наклеить на каждый мешок имя (букву латинского алфавита). Различных предметов, которые вы положите в эти мешки, должно быть не более 20 – тогда список предметов поместится в заготовленные таблицы.

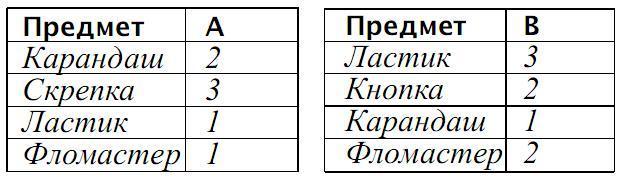
Каждый учащийся получает свой мешок (пакетик) и составляет таблицу этого мешка (три бланка таких таблиц помещены на с. XVII вкладыша). Для заполнения таблицы ребенку придется составить список названий предметов мешка. Можно посоветовать детям вынимать предметы из мешка, одновременно дописывая в левый столбец таблицы названия тех предметов, которые ему еще не встречались. После этого останется подсчитать, сколько раз каждый из предметов встретился в мешке, и заполнить таблицу.

Затем работа ведется всем классом. Нужно составить один общий список всех предметов, которые есть в мешке хотя бы у одного ученика в классе. Для этого первый ученик выписывает на доске названия всех предметов из своего мешка. Затем второй ученик дописывает названия тех предметов, которые есть в его мешке, но еще не внесены в список. Все остальные ученики контролируют ход работы.

Продолжает запись следующий ученик. Постепенно в списке оказываются все предметы.

Далее можно организовать два варианта работы: индивидуальный и групповой. В первом случае каждый ученик работает с этой задачей так же, как он работал с задачей 1. Он заполняет сводную таблицу на с. XVIII, разрезает ее на отдельные столбцы и находит два одинаковых. Единственное отличие от задачи 1 состоит в том, что у каждого ученика имеется только одна таблица для своего мешка. Чтобы дети могли заполнить сводную таблицу, необходимо организовать обмен информацией. На доске записан общий список предметов. Попросите всех по очереди выйти к доске и выписать столбец для своего мешка. Так каждый ученик сможет заполнить сводную таблицу (переписав с доски) и самостоятельно найти два одинаковых столбца.

Для другого варианта работы – группового – каждый ученик должен заполнить таблицу для своего мешка на с. XVII еще раз, но уже с новым списком предметов. Перечень и порядок предметов в таблице должны теперь быть в точности такими же, как в общем списке на доске. Напротив названий тех предметов из списка, которых в мешке у учащегося нет, ставится ноль. Далее происходит поиск одинаковых таблиц. При этом если раньше мы делили на кучки столбцы таблицы, то теперь на группы делятся дети. Например, первый ученик говорит: «У меня в первой строчке единица, у кого тоже?» Все дети, у кого в первой строчке 1, подходят к нему. Учитель спрашивает у одного из оставшихся сидеть, какое у него число в первой строчке. Ученик отвечает, и к нему подходят все, у кого в первой строчке такое же число. Образуется несколько довольно больших групп учеников. Каждая из этих групп должна теперь разделиться на несколько подгрупп с одинаковыми числами во второй строке и т. д.

Постепенно групп становится все больше, а детей в группах все меньше. В конце концов совпадающие таблицы будут найдены и останется только проверить результат, достав элементы из мешков. Не исключено, что при этом дети обнаружат ошибки.

Ошибки могут быть двух типов:

1. Ученик неправильно составил таблицу мешка.
2. Два разных предмета были названы одинаково. Например, дети считали карандаши, а после проверки оказалось, что у одного карандаш красный, а у другого синий. Скрепки могут оказаться разного размера.

В этом случае необходимо довести работу по сравнению мешков до конца, внеся изменения в таблицы. Обязательно надо обсудить, можно ли было из-за этой ошибки пропустить одинаковые мешки.

Можно организовать и телесное составление таблиц мешков. Для этого понадобится горизонтальная поверхность, на которой следует нарисовать таблицу такого размера, чтобы в любой ее клеточке можно было положить все одинаковые элементы одного мешка. Еще лучше сделать каждый столбец таблицы в виде отдельной картонки, фанерки или полоски лоточков. Такая конструкция таблицы позволит сортировать ее столбцы с разложенными на них предметами.

Рассмотрим пример организации работы с телесной таблицей. Сначала каждому мешку присваивается номер или имя (скажем, имя держащего его ученика). Если в классе несколько учеников с одинаковыми именами, то придется использовать и имя, и фамилию. Затем каждый подписывает один столбец таблицы именем своего мешка. После этого начинается заполнение таблицы элементами мешка. Один ученик достает из своего мешка первый попавшийся ему элемент, называет его и кладет в верхнюю ячейку таблицы. Например: «В верхнюю ячейку таблицы я положу скрепку». Слово «скрепка» записывается на доске, и все ученики, которые находят в своих мешках скрепки, кладут их в свою верхнюю ячейку. Затем тот же или любой другой ученик достает из мешка следующий предмет, называет его и кладет во вторую сверху ячейку. Постепенно все предметы из всех мешков оказываются выложенными в таблицы, причем у всех учеников в одинаковых строчках лежат одинаковые предметы. По завершении первого этапа работы следует приступить к сортировке таблиц. Ее можно проводить так же, как и описанную выше сортировку обычных таблиц. Во время сортировки иногда выясняется, что при заполнении таблиц разные предметы были названы одинаково. Например, в первую строчку решили поместить карандаши, а когда таблицы положили рядом, выяснилось, что в одном мешке карандаши синие, а в другом – красные. Придется заполнить в таблице новую строчку, написав в ней, скажем, «карандаши красные», а старую строчку «карандаши» исправить на «карандаши синие».

Выполнив проект, дети получают инструмент нахождения одинаковых мешков, одинаковых массивов, независимо от количества элементов в мешках и числа мешков. Главное, что должно остаться у детей, – это ощущение могущества придуманного ими способа решения задачи о нахождении одинаковых мешков; возможно, работа будет долгой, но она обязательно приведет к результату.