Информатика. 3 класс Демо+методичка

Урок 3. «Таблица для мешка (по двум признакам)»

Мешки-векторы

Ребята уже знакомы с мешками и одномерными таблицами для мешков. Надеемся, что работа с данными математическими объектами не вызовет у учащихся особых трудностей. Однако для математики введение этих объектов оказалось достаточно важным шагом. Дело в том, что числа, прежде всего натуральные, очень удобны для измерений, например, времени (скажем, в секундах), или веса (в граммах), или пройденного расстояния (в метрах). Но если мы хотим указать, не сколько мы прошли, а куда пришли, то ситуация становится сложнее. Нам приходится указывать два «измерения» – два числа или два символа. Это похоже на то, как мы указываем положение в городе (например, говорим: «угол Ленина и Розы Люксембург») или положение фигуры на шахматной доске (например, e2). Самый распространенный в математике способ состоит в том, что на поверхность наносится сетка, как на бумаге в клетку. Если взять лист клетчатой бумаги, то с каждой клеткой на нем можно сопоставить два натуральных числа. Одно из этих чисел означает, сколько шагов надо сделать из нашей клетки, чтобы оказаться у левого края листа, а другое – сколько шагов надо сделать, чтобы добраться до нижнего края. Два таких числа называют координатами квадратика, их нельзя поменять местами – это не просто мешок, в котором лежат два числа, но упорядоченная пара (цепочка!), о которой мы договорились, что первое число – всегда расстояние до левого края листа, а второе – расстояние до нижнего края.

Тем не менее координаты можно сложить в мешок. Для этого понадобятся бусины двух типов: бусина одного типа будет обозначать один шаг влево, а бусина другого – один шаг вниз. Какими именно будут бусины – вопрос договоренности. Например, квадратными и круглыми или синими и зелеными. А могут быть карточки, на которых написано «влево» и «вниз». Таким образом, каждой клетке на листе можно сопоставить мешок, в котором будет сколько-то бусин «влево» и сколько-то бусин «вниз».

Построив одномерную таблицу такого мешка, получим пару чисел, аналогичную координатам: ведь в таблице для каждого числа ясно, число каких именно карточек оно обозначает. Получится так называемый вектор. Конечно, вектор может иметь не только два, но и больше параметров (соответствующая цепочка чисел может быть длиннее). И в нашем мешке могут тоже лежать бусины многих типов. В отличие от множества в мешке (мультимножестве) может быть несколько объектов одного типа. Значит, в таблице для мешка будут не только единицы и нули.

С понятия вектор начинается изучение науки, которую называют аналитической геометрией. Данное понятие лежит в фундаменте всей физики и многих разделов математики.

Тема нового урока – двумерные таблицы для мешков. С научной точки зрения двумерные таблицы – это следующая по сложности структура, набор векторов. Конечно, мы не будем наших детей сейчас нагружать этой сложной терминологией. Достаточно того, что они научатся сортировать и классифицировать элементы мешка по двум признакам и аккуратно заполнять таблицу.

Решение задач из учебника

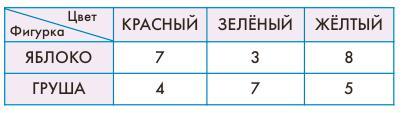
Задача 14. В мешке G довольно много фруктов. Если кто-то из детей запутается, посоветуйте ему как-то помечать посчитанные фигурки. Именно для этого мы поместили в рабочую тетрадь копию мешка. Итак, выберем некоторую клетку в таблице и будем искать в мешке все фрукты соответствующего вида и цвета. При этом будем помечать посчитанные фрукты в мешке – обводить, вычеркивать и т. п. Если по окончании заполнения таблицы не все фигурки окажутся помеченными, можно будет легко найти, какая клетка в таблице заполнена неверно, и исправить ошибку. Возможно, дети в ходе решения будут использовать и другие стратегии. Например, будут считать сначала все желтые фрукты – яблоки, а потом – груши.

Ответ:

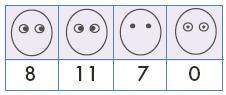
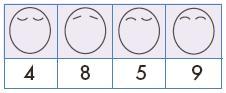
Задача 15. Сначала требуется заполнить четыре (одномерные) таблицы, т. е. классифицировать лица поочередно по четырем различным признакам – виду носа, виду рта, виду глаз и виду бровей. Перед сильным ребенком можно поставить вопрос, как проверить правильность заполнения этих четырех таблиц: сумма чисел в каждой таблице должна быть одной и той же. Попросите ученика объяснить, почему так получается. Действительно, по какому бы (одному) признаку мы ни классифицировали лица, в сумме мы должны получить то количество фигурок, которое лежит в мешке.

Ответ (одномерные таблицы):

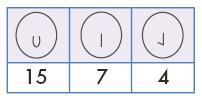
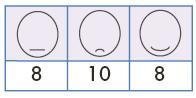
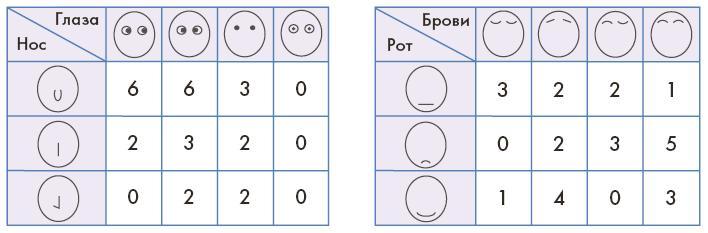
Вторая часть задачи – заполнение двумерных таблиц – технически более сложная. Трудность, во-первых, состоит в том, что дети должны помнить одновременно два признака и полностью отключиться от остальных. Во-вторых, признаки хотя и осмысленные, но однотипные (палочки и закорючки), поэтому легко путаются, а предметы в мешке при этом не различаются ни формой, ни размером, ни цветом. В-третьих, одновременно с поиском лиц ученик должен их еще и считать. Задание специально составлено таким образом, чтобы каждый ребенок почувствовал необходимость выработки собственной системы работы. Если кто-то начал запутываться, стоит помочь ему – обсудить, какую именно систему ребенок использует для работы, или выработать такую систему в совместном обсуждении. В зависимости от того, к чему будет склоняться ученик, мы предлагаем вам один из трех возможных подходов.

Первый подход состоит в том, чтобы заполнять клетки таблицы поочередно, т. е. искать каждый раз все те лица, в которых присутствуют два признака, соответствующие этой клетке. Основные проблемы при такой работе:

1. Соскальзывание с эталона – при переводе внимания с таблицы на объекты мешка ребенок может забывать, какие именно признаки он ищет в данный момент, и переключаться на другие.
2. Сложность одновременно искать лица и считать их, даже пользуясь различными пометками.

Для устранения первой проблемы можно использовать шаблон: нарисовать на черновике глаза и нос, которые он ищет, и периодически поглядывать на этот образец. Для устранения второй проблемы можно использовать пометки: сначала найти и пометить все лица, а потом их сосчитать. Необходимо только помнить – пометки должны быть такие, чтобы дети не путали лица, помеченные на текущем и предыдущих этапах. Для этого можно использовать разные цвета пометок, или, наоборот, работать простым карандашом и стирать пометки после каждого этапа работы.

Второй подход состоит в том, чтобы поочередно брать лица из мешка и соотносить их с определенной клеткой в таблице. Например, лицо в левом нижнем углу имеет рот прямой черточкой и нахмуренные брови, значит, оно должно находиться в верхней клетке самого левого столбца второй таблицы. Ставим в этой клетке палочку карандашом и соответствующее лицо в мешке тоже помечаем карандашом (например, обводим). Когда все лица в мешке окажутся помеченными, подсчитаем палочки в каждой клетке таблицы и заменим их на полученные числа.

Третий подход – скопировать страничку учебника, вырезать все фигурки из мешка и рассортировать их на столе по необходимым признакам. Подсчитав, сколько фигурок оказалось в каждой кучке, заполнить таблицу. Этот способ самый простой. Не стоит его предлагать детям, которые хоть как-то справляются без него. Но если вы видите, что ребенок никак не может сосредоточиться (внимание рассеивается), предложите ему этот способ и выдайте копию странички.

Выработав вместе с ребенком систему работы, подходите к нему время от времени и обсуждайте снова, что он делает. После того как все дети определились со стратегией и начали  работать, возможно, ребят начнут посещать идеи о соотношении одномерных и двумерных таблиц и о том, как это можно использовать при решении и проверке. Например, многие ребята заметят, что лиц с одним из видов глаз в мешке нет. Кто-то сделает совершенно справедливый вывод, что комбинации этого вида глаз со всеми формами носа тем более отсутствуют, поэтому во всех строках последнего столбца левой двумерной таблицы можно сразу написать нули. Можно и дальше продолжить обсуждение соотношения одномерных и двумерных таблиц в ходе проверки. Например, спросить ребят: «Где в левой двумерной таблице находятся все лица с округлым носом?» (Ясное дело, в верхней строке.) «А сколько у нас всего лиц с круглым носом?» Эту информацию можно найти в первой одномерной таблице – таких лиц всего 15. Вывод: сумма всех чисел в верхней строке должна быть равна 15. Если у ученика это условие выполняется, он может переходить ко второй строке, если нет, пусть ищет ошибку в клетках верхней строки. После проверки по строкам можно провести проверку по столбцам на основании информации третьей одномерной таблицы. Если все сходится, это гарантирует правильность заполнения двумерной таблицы (конечно, при условии, что одномерные таблицы перед этим были заполнены верно). Таким образом, отпадает необходимость фронтальной проверки. Напоминаем, что самая полезная проверка – это проверка, в ходе которой ребенок самостоятельно нашел свои ошибки.

Ответ (двумерные таблицы):

Задача 16. Наверняка наибольшее число ошибок при решении этой задачи будет связано с заливкой «фона», который на нашей картинке состоит из трех областей, две из которых относительно небольшие, а третья занимает весь оставшийся «фон».

Обсудите с ребятами, где они могли видеть этот знак. Можно дать задание поискать дома упаковки с таким экологическим знаком и принести их на следующий урок. Можно также попросить ребят подумать дома, зачем на товарах рисуют подобный знак, хорошо это или плохо, что товар помечен этим знаком, и т. п.

Ответ: в этой картинке девять областей (каждая из трех стрелок содержит две области и еще три области «фона»).

Задача 17. Необязательная. Структуры, аналогичные цепочкам и мешкам, можно встретить где угодно, и в том числе, конечно, в сказках. Даже житейских знаний ребят окажется достаточно, чтобы выполнить данную задачу. Тем не менее перед решением задачи каждый из детей должен уяснить для себя, что ряд домочадцев, тянущих репку, – это цепочка, первая бусина которой – дедка, а последняя – мышка. В этой задаче дети повторяют все понятия, связанные с порядком бусин в цепочке, в том числе понятия, касающиеся частичного порядка (например, «вторая перед Жучкой»). Обратите внимание, что в утверждениях, использующих понятия раньше/позже, может быть несколько верных решений.

Ответ:

Дедка тянет из земли репку.
Следующая после бабки – внучка.
Предыдущая перед мышкой – кошка.
Последней тянет мышка.
Вторая перед Жучкой – бабка.
Третья после внучки – мышка.
Жучка тянет репку раньше кошки/мышки.
Мышка тянет репку позже кошки/Жучки/внучки/бабки/дедки.

Задача 18. Необязательная. Различные пары слов в мешках не связаны между собой, поэтому, начав с любой пары слов, ученик дойдет до правильного решения. Любое частичное решение может быть продолжено до полного, любая пара сопоставленных слов является частью окончательного решения. При таком произвольном построении не возникает «тупиков». Далеко не все задачи курса обладают таким свойством автономности каждой части решения. Задачи бывают и более запутанными, при сопоставлении слов мы могли бы отождествить два слова, заполнив пробелы, а потом оказалось бы, что это отождествление не удается продолжить до решения всей задачи, потому что другое слово с пробелами «осталось безработным». Задачи с подобными «тупиками» появятся в курсе позднее.

Ответ: слова МОЛОТОК и МОЛОКО.

Компьютерный урок «Таблица для мешка», задачи 17 – 24

Задача 17. Эта задача полностью аналогична задачам на заполнение двумерной таблицы из учебника. Как и в задачах учебника, здесь можно посоветовать запутавшемуся ученику использовать пометки, например, помечать галочками сосчитанные фигурки. Также удобно использовать клетки таблицы слева направо и сверху вниз.

Задача 18. Здесь, как и в предыдущей задаче, клетки таблицы стоит использовать в некотором порядке, например, слева направо и сверху вниз. При этом полезно помечать клетки таблицы, которые уже использованы.

Задача 19. Как видите, эта задача сложней и интересней предыдущей. Здесь необходимо соблюсти сразу 3 условия – показания двух одномерных таблиц и то, что все фигурки должны быть разными. Это накладывает серьезные ограничения на искомый мешок. Для начала замечаем, что каждая фигурка в библиотеке трех цветов. Значит, надо начать с фигурок, которых во второй таблице по три. У нас в библиотеке имеется ровно 3 разные груши и 3 разные сливы, поэтому кладем их в мешок, ведь других вариантов у нас нет. После этого обратимся к первой таблице. Мы уже положили в мешок по две фигурки каждого цвета, значит, осталось положить одну красную, одну зеленую и две желтые. При этом среди них должно быть два яблока и два банана. Сделать это можно по-разному, поэтому решений в этой задаче несколько.

Задача 20. В этой задаче ребята повторяют понятие «цепочка цепочек». В данном случае ребята работают с цепочкой цепочек, длина которой равна 4. Из истинности последнего утверждения вытекает и истинность предыдущего, поскольку все пустые цепочки одинаковы. Таким образом, из данных утверждений ровно 3 истинны, а остальные – ложны.

Задача 21. Задача на повторение лексики, отражающей частичный порядок бусин в цепочке. Заметим, что среди данных слов имеются такие, для которых данное утверждение не имеет смысла – это слова, в которых две буквы А, и слова, в которых нет второй после А буквы. В результате мы находим 6 подходящих слов: БАЛКОН, БАНКЕТ, БАНК, БАНКИР, БАШКИР, БАСКЕТБОЛ.

Задача 22. Задача на повторение календарного порядка. Поскольку здесь все даты принадлежат к разным месяцам, то для решения достаточно перебирать месяцы, начиная с октября (первой даты цепочки) и до сентября (последней даты в цепочке).

Задача 23. В этой задаче речь идет о цепочке дней недели. Эта цепочка не представлена явно, но детям она хорошо известна. Отличие ее от наших цепочек в том, что она не имеет фиксированного начала и конца. Мы, конечно, можем рассмотреть цепочку дней одной недели, но при этом хорошо понимаем, что перед понедельником было воскресенье, а после воскресенья опять будет понедельник. То есть, по сути, структура у нас не линейная, а циклическая. При этом структура направленная, поскольку для дней недели можно четко определить следующий и предыдущий день. Именно поэтому среди утверждений нет ни одного, касающегося общего порядка дней недели, то есть порядка относительно начала или конца цепочки. Все утверждения относятся к частичному порядку – порядку бусин друг относительно друга. При этом ясно, что понятие «завтра» аналогично нашему понятию «следующий», а понятие «вчера» – понятию предыдущий. Что касается понятий «позавчера» и «послезавтра», то они аналогичны понятиям «второй перед» и «второй после».

Задача 24. Необязательная. Как видите, эта задача – типичная практическая информационная задача. Подобные задачи (в отличие от традиционных задач нашего курса) характеризуются тем, что кроме информации, изложенной на листах определений учебника, нужно привлекать информацию из окружающего мира. В нашем курсе обычно используются общеизвестные факты или же те, о которых ребенок может легко догадаться. Так, в данном случае даже далекий от музыки ребенок в состоянии догадаться, что струнными называются инструменты, в которых имеются струны, а клавишными – в которых имеются клавиши. Также дети смогут сообразить, что понятие «духовые» – от слова «дуть», а «ударные» –  от слова «ударять».