Информатика. 2 класс Демо+методичка

Урок 33. «Выравнивание, решение необязательных задач», 2 полугодие

Если у вас есть возможность, мы советуем вам после второй контрольной работы, как и после первой, провести урок выравнивания (подробней об уроках выравнивания см. в комментарий к уроку «Выравнивание, решение необязательных задач, 1 полугодие»).

Решение задач из учебника

Задача 212. Решений здесь имеется два. Поскольку условием не определяется только место совы в цепочке – она может быть первой или последней. Оставшаяся часть цепочки определяется однозначно: синица – попугай – орел – курица – петух – сорока.

Задача 213. Здесь мы предлагаем детям решить задачу, аналогичную задаче 208 из учебника, только не о днях недели, а о месяцах. Это практическая задача, поскольку она использует разговорную лексику, однако эта лексика имеет аналоги в нашем курсе. Так языковое выражение «через месяц» аналогично понятию «следующий месяц» в нашем курсе, а выражение «месяц назад» аналогично понятию «предыдущий месяц».

Задача 214. Здесь поиск приходится вести среди всех слов нашего Словаря. Первое утверждение проверять проще, чем второе. Поэтому стоит вести поиск всех слов с последней буквой А. Среди таких стоит выделять слова, в которых есть буква Я и для них внимательно проверять второе утверждение. Итак, начинаем перебор с первого слова. Первое слово с последней А – АНГИНА, но в нем нет Я, поэтому пропускаем его. Точно такая же ситуация со словами: АПТЕКА, БЕЛКА, БУКВА, БУТЫЛКА и т. д. Первое по счету слово с последней А, в котором есть буква Я – слово НЯНЬКА. Для него проверяем второе утверждение, видим, что оно истинно. Значит, мы уже нашли нужное слово. Заметим, что в Словаре такое слово единственно.

Задача 215. Необязательная. Конечно, эта задача имеет ровно одно решение. Поскольку в русском языке всего 10 гласных букв, именно они и должны лежать в искомом мешке.

Задача 216. Необязательная. Эта довольно сложная задача взята из обыденной жизни, окружающей второклассника. Для детей, в большей степени включенных в реальную жизнь (благодаря самостоятельности или своевременной помощи родителей), задача может оказаться совсем простой. Детей с «чисто академическими» знаниями (таблица умножения и куча стихов наизусть) эта задача может поставить в тупик. Вероятно, некоторые дети не поймут смысл вывески универмага. Объясните им, что квадратики справа означают дни недели: синие соответствуют рабочим дням, красный – выходному. Если ребенок не может догадаться сразу, какой день выходной, пусть сосчитает синие квадратики и дни недели.

Ответ: первое, третье и последнее утверждение истинные, остальные – ложные.

Задача 217. Необязательная. В целом эта задача сложная – окон много, а информации в обрез; кроме того, есть несколько ловушек. Для начала нужно выделить утверждения, которые можно использовать сразу (то есть те, в которых речь идет о станциях, уже помеченных на схеме). Здесь ребята сталкиваются с первой интересной особенностью задачи – в условии есть утверждения, которые уже истинны, поэтому их нужно сразу пометить (они нам не пригодятся) – это четвертое и седьмое утверждения. Теперь найдем условия, которые можно использовать сразу – это третье, предпоследнее и последнее утверждения. В результате мы поместили в схему станции: Тверская, Театральная и Коломенская (заметим, что шестое утверждение при этом становится истинным автоматически). Теперь прочтем первое, второе и пятое утверждения. Конструкции «вторая после» и «вторая перед» говорят о том, что станции: Аэропорт, Сокол, Войковская и Динамо, мы должны поставить в 4 подряд идущих пустых окна. Правильную последовательность учащийся может получить в ходе проб и ошибок, в ходе сопоставления двух фрагментов (Войковская – Аэропорт, Сокол – Динамо)  или в ходе одновременного анализа трех утверждений. Главное, чтобы, обнаружив ошибку, ребенок терпеливо вернулся к началу этого фрагмента и попробовал другой вариант. Наконец, у нас осталось одно пустое окно и одно утверждение, которое дает нам название недостающей станции. Несмотря на то, что решение этой задачи вы, наверняка доверите сильным ученикам, они вряд ли будут рассуждать столь четко, да и не надо этого от них требовать. Однако, приведенные здесь рассуждения помогут вам сдвинуть учащегося с мертвой точки, не подсказывая ему решения. Посоветуйте детям сначала писать простым карандашом. И конечно, недопустимо, чтобы дети просто списывали решение со схемы линий метро.

Задача 218. Необязательная. Это не очень сложная задача и многие дети решат ее быстро. При этом большинство ребят слово просто угадают. Слабым учащимся можно подсказать, что это слово обозначает день недели. Вообще слов обозначающих дни недели из 11 букв всего два, поэтому перебор будет совсем не большим.

Задача 219. Необязательная. Утверждений в описании здесь достаточно много, но шаблоны для слов в цепочке однозначно определяют каждое слово, поэтому здесь невозможно зайти в тупик. Это означает, что если ребенок смог (по окнам и буквам) вписать одно из слов, упоминаемых в утверждении, в цепочку, то сделал это правильно. Поэтому содержание данных утверждений можно было бы вообще не анализировать, а вписывать каждое слово просто туда, куда оно подойдет. Но дети, конечно, заметят эту особенность не сразу, поэтому будут использовать утверждения достаточно активно.

Задача 220. Необязательная. Задача на повторение алгоритма подсчета областей картинки. Как видите, эта задача не слишком сложная, ее можно предложить практически любому ученику в классе.

Ответ: в этой картинке 6 областей.

Задача 221. Необязательная. Аналогичные задачи детям уже встречались (см. комментарии к задаче 207 из учебника).

Ответ: слово НАЧАЛО идет в Словаре раньше слова НЕДЕЛЯ.

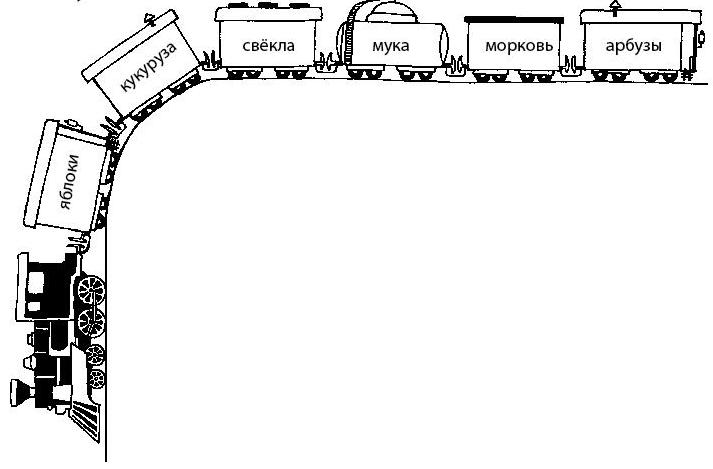
Задача 222. Необязательная. Естественно, начать решение учащийся должен с определения начала и конца цепочки. Затем стоит выделить и использовать те утверждения, которые определяют положение вагонов однозначно, так мы находим положение вагонов с мукой, а затем – с морковью. Далее ребята могут пробовать разные варианты, имея в виду, что для свеклы и кукурузы необходимо найти два подряд идущих вагона.

Ответ:

Задача 223. Необязательная. В этой задаче дети повторяют понятие «каждый» и заодно вспоминают, что две симметричные фигурки в нашем курсе считаются разными.

Компьютерный урок «Выравнивание, решение необязательных задач»

Решение задач 225 – 232

Задача 225. В силу первого и второго утверждений первая бусина в цепочке – красная круглая, а последняя – синяя квадратная. В силу последнего утверждения вторая бусина в цепочке – оранжевая круглая, а предпоследняя – зеленая треугольная. Наконец, учитывая третье утверждение на третье место в цепочке нужно поставить фиолетовую бусину (любой формы), а на четвертое – голубую (также любой формы).

Задача 226. Вначале здесь стоит определиться, в каком порядке использовать утверждения. Лучше всего начать с последнего утверждения и поставить буквы О на второе и пятое место. Теперь попробуем найти место для буквы Т. Поскольку третье и четвертое утверждения должны иметь смысл, то в цепочке должна существовать как третья буква перед Т, так и третья буква после Т. Оказывается, что буква Т может стоять только на четвертом месте. Дальше решение достроить совсем не сложно. Получаем слово ВОСТОРГ.

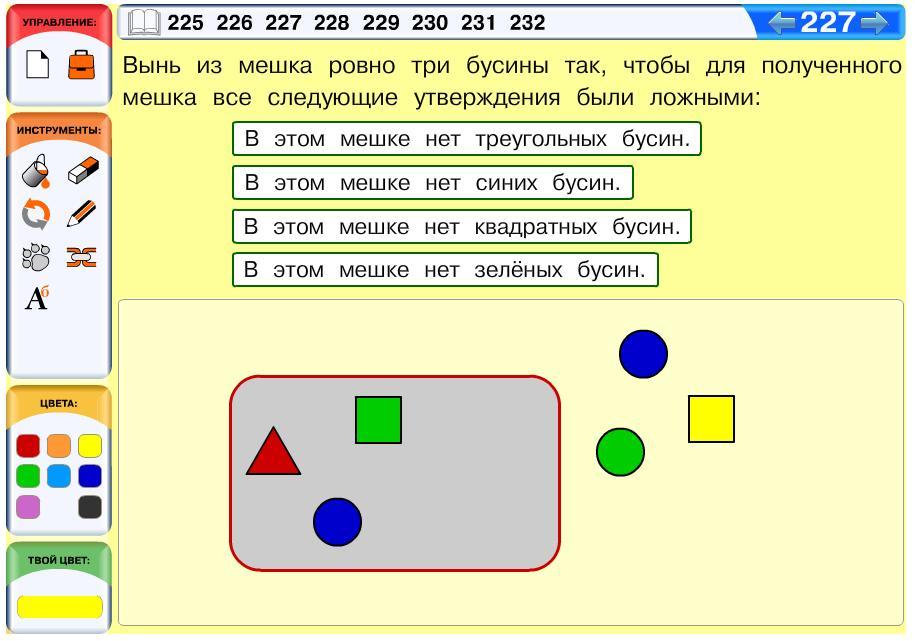
Задача 227. Здесь нам нужно достроить мешок, чтобы он соответствовал системе ложных утверждений. Конечно, хорошо бы сразу переформулировать описание в виде совокупности истинных утверждений. Получаем следующее:

В мешке есть треугольные бусины.

В мешке есть синие бусины.

В мешке есть квадратные бусины.

В мешке есть зеленые бусины.

Конечно, исходный мешок соответствует этому описанию. Но нам надо вынуть из него три бусины так, чтобы полученный мешок также соответствовал этому описанию. Треугольная бусина в мешке одна, значит, ее вынимать нельзя. Квадратных бусин в мешке две, причем одна из них зеленая, значит, пока на всякий случай вынем другую (про цвет которой в условии не сказано ничего). Круглых бусин у нас три, причем две – синие и больше синих бусин в мешке нет. Значит обе синие бусины вынимать нельзя, вынимаем одну синюю. Видим, что также можно вынуть из мешка и круглую зеленую, ведь в мешке есть еще одна зеленая бусина (квадратная). Теперь мы вынули из мешка три бусины. Проверяем, что для получившегося мешка все исходные утверждения ложны.

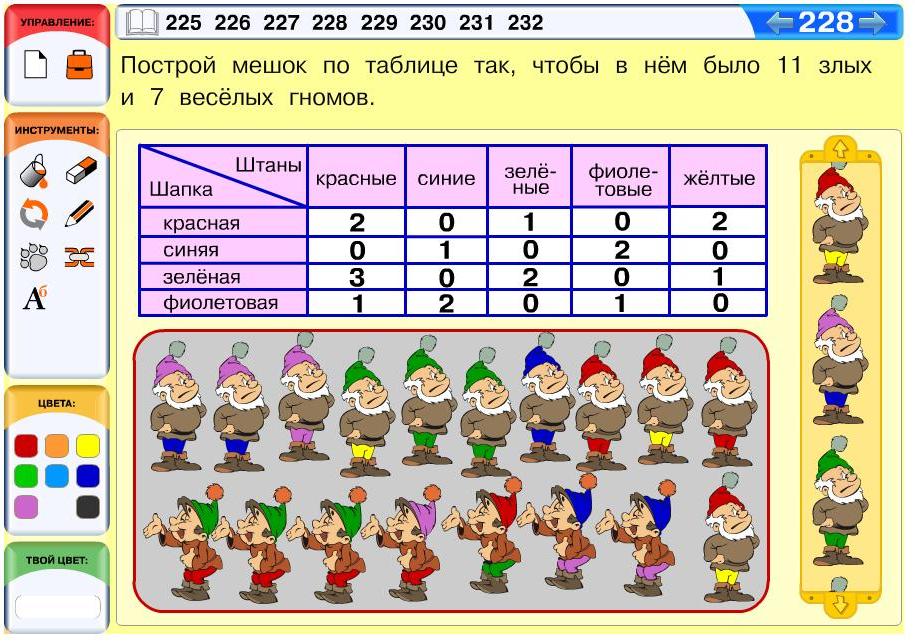
Задача 228. Сложная задача, предназначенная для средних и сильных учащихся. Эта задача на построение мешка по двумерной таблице, но при этом надо соблюсти дополнительное условие (в мешке должно быть 7 веселых и 11 злых гномов). Несколько упрощает решение набор фигурок в библиотеке, главное – выбрать, с какой клетки таблицы лучше начать. Так, видим, что веселых гномов в желтых штанах, в таблице просто нет, значит, придется выбирать злых. По таблице берем двух таких в красной шапке и одного в зеленой шапке. Также однозначно определяются многие клетки таблицы. Например, гномы в красных штанах и красной шапке есть тоже только среди злых гномов, а вот гномы в зеленых штанах и красной шапке – только среди веселых гномов. После того как мы используем все клетки таблицы, которые дают однозначную информацию о мешке, посчитаем число злых  и веселых гномов. У нас оказалось 9 злых гномов и 4 веселых. Теперь добавим в мешок 2 злых и 3 веселых гномов так, чтобы среди них были 3 гнома в зеленой шапке и красных штанах и 2 гнома – в фиолетовой шапке и синих штанах (это можно сделать по-разному).

Задача 229. Аналогичная задача ребятам уже встречалась (см. комментарии к компьютерной задаче 202). В данном случае в окнах следует написать слова: ВЫХОД, ПАЛКА, СОЛЬ, САЛАТ (или ЛАСТА).

Задача 230. Достаточно интересная задача, которая подходит практически для всех учащихся. Для начала у нее не совсем обычная формулировка. На первый взгляд все эти сочетания чисел и слов похожи на календарные даты. Однако, при более внимательном рассмотрении видим, что это не так. В одной из дат использован несуществующий месяц, а в других – числа, которых в соответствующем месяце нет, например, 30 февраля, 31 сентября, 31 апреля. После того, как дети отобрали из данных все календарные даты, задачи становится стандартной.

Задача 231. Здесь одновременно придется соблюсти несколько условий, строя мешок по описанию. В таких случаях наиболее актуальным является вопрос, с какого утверждения лучше начать. Как обычно, мы советуем начать с того условия, которое дает однозначную информацию о мешке. В данном случае это последнее условие, ведь знаков с изображениями людей в нашей библиотеке всего 5 (все фигурки в мешке должны быть разными). Такие знаки можно сразу положить в мешок. Теперь в мешок осталось положить 7 знаков, таких, чтобы: 5 знаков было со стрелками, 3 с красной рамкой и 4 с синей рамкой. Поскольку знаков со стрелками нам нужно положить 5, а знаков с синей рамкой 4, нужно обязательно взять знак со стрелкой с красной рамкой и все знаки в синей рамке нужно обязательно взять со стрелками.

Задача 232. Несмотря на то что эта задача из разряда лингвистических, для ее решения достаточно знания кириллического и латинского алфавита (по сути, она на повторение латинского алфавита). Обратите внимание, все слова здесь написаны строчными буквами. Об этом можно судить, глядя на буквы, которые в строчном и заглавном вариантах пишутся по-разному. В данном случае в каждом слове имеется хотя бы одна буква, которая позволяет однозначно отнести слово к одному из языков. Например, в слове «cable» есть латинская буква «b», а в слове «сунар» кириллическая буква «н».