Информатика. 2 класс Демо+методичка

Уроки 30–31. «Круговая цепочка. Календарь»

К настоящему моменту дети хорошо знакомы с цепочками разных объектов. Ребятам приходилось выбирать, достраивать и строить цепочки по описанию, использовать цепочки для решения задач. Кроме того, учащиеся научились оперировать многими понятиями, относящимися к порядку элементов в цепочке: первый, второй, третий, последний, следующий/предыдущий, второй после/третий перед, раньше/позже и т.д. Наверняка многие из ребят уже могут выделить цепочки в окружающем мире. Вот только некоторые из таких примеров: очередь в магазине, радиальная ветка метро, цепочка букв в слове, цепочка цифр в натуральном числе, цепочка слов в предложении, цепочка дней одной недели, расписание уроков на один учебный день, цепочка месяцев одного года, список учеников класса и проч.

Однако, перечисляя примеры цепочек из окружающего мира, трудно не заметить, что некоторые процессы в природе имеют циклический характер, то есть элементы в них идут друг за другом по кругу и, по сути, не имеют четких начала и конца. Этот круг при желании можно разорвать, выделив цепочку, если нужно. Так мы поступаем, говоря о цепочке дней одной недели. Но при этом мы понимаем, что после воскресенья одной недели идет понедельник другой недели, поэтому чередование дней недели на самом деле идет по кругу. Аналогично дело обстоит с чередованием: времен года, времени суток, месяцев. Все эти явления окружающего мира чрезвычайно важны для детей начальной школы. Поэтому было бы странным избегать их рассмотрения. Не совсем правильно было бы рассматривать их и как обычные цепочки, ведь ребенок должен знать, что после декабря идет январь, а после воскресенья – понедельник. Поэтому в курсе мы выделяем такие циклические объекты в отдельный класс и называем их «круговые цепочки». Ясно, почему на листе определений употребляется слово «круговые» – все объекты в таких цепочках идут как бы по кругу. Если кто-то из ребят спросит, почему такие объекты называются «цепочками» и вообще причем здесь цепочки, можно поговорить с ребятами о сходствах и различиях обычных цепочек и круговых цепочек. Как и в обычных цепочках, в круговых цепочках элементы идут друг за другом в определенном порядке. Это означает, что, как и обычная, круговая цепочка имеет направление и частичный порядок. Например, мы знаем, что после марта всегда идет апрель, а не наоборот. Поэтому мы можем употреблять по отношению к элементам круговой цепочки все понятия, связанные с частичным порядком элементов, например: следующий (предыдущий) или второй после (третий перед). Отличие круговой цепочки в том, что в ней нет начала и конца и, соответственно, первого, второго, третьего, последнего элемента. Таким образом, по отношению к элементам круговой цепочки нельзя употреблять все понятия, характеризующие общий порядок элементов и связанные с ними понятия «раньше» (ближе к началу) и «позже» (ближе к концу). Видим, что обычная и круговая цепочки имеют как сходства, так и различия. Употребление слова «цепочка» здесь связано с тем, что так дети скорее перенесут свои знания о цепочках на новые объекты. Чтобы дети осуществляли перенос правильно, на листе определений явно перечислены отличия круговой цепочки.

Заметим, что построение из одних и тех же объектов обычной и круговой цепочки не несет в себе никаких логических или практических противоречий и не должно смущать детей – мы в курсе будем делать это регулярно. Дело в том, что при построении обычной цепочки для циклического чередования теряются некоторые связи, не отражается всего количества порядков. Но, с другой стороны, человеку свойственно вычленять из времени некоторые конечные отрезки определенной протяженности, например при планировании своей деятельности. Поэтому человеку часто удобнее работать с конечными цепочками, чем с круговыми. Таким образом, как обычно, мы выбираем то или иное представление информации, исходя из конкретной задачи – так и в данной теме мы выбираем представление объектов в виде обычной или круговой цепочки в зависимости от поставленной задачи. В учебных задачах всегда будет указано явно, какую цепочку необходимо построить, поэтому никакой путаницы у ребят быть не должно.

На данном листе определений рассмотрен пример одной из наиболее распространенных круговых цепочек – цепочки дней недели. Остальные наиболее важные для первоклассников круговые цепочки будут подробно рассматриваться в задачах. Поэтому все обязательные задачи данного урока необходимо решить всем учащимся.

Решение задач из учебника

Задача 200. В этой задаче ребята продолжают работать с круговой цепочкой дней недели, рассмотренной на листе определений. Предполагается, что они будут отвечать на вопросы с опорой на построенную цепочку. Конечно, дети могут назвать следующий день после четверга, исходя из практических знаний о чередовании дней недели. Однако им трудно будет мысленно отыскать десятый день после воскресенья – в этом случае дни недели лучше отсчитывать непосредственно. Правописание названий дней недели дети также уточняют в цепочке, приведенной на листе определений.

Задача 201. Месяцы одного года образуют обычную цепочку, поскольку любой год начинается с января (это первый месяц года) и заканчивается декабрем (это последний месяц года). Такая цепочка детям должна быть хорошо известна. Однако если обсуждать чередование месяцев вообще, без учета года, то получается уже круговая цепочка, поскольку после декабря одного года идет январь следующего года. Такое представление о чередовании месяцев детям тоже полезно иметь. В данной задаче, как и в предыдущей, дети работают по готовой, построенной цепочке – отвечают на вопросы, касающиеся частичного порядка месяцев (то есть порядка друг относительно друга). На первые 3 вопроса многие дети смогут ответить вообще без опоры, исходя из практических знаний о чередовании месяцев. На остальные вопросы большинство ребят будут отвечать, отсчитывая месяцы в цепочке. Поскольку месяцев в году всего 12, двенадцатый месяц после данного или перед ним – это тот же самый месяц. Некоторые дети поймут это сразу, некоторые – в процессе ответа на четвертый вопрос.

Задача 202. Как уже говорилось, человеку в процессе планирования своей деятельности часто удобней работать не с круговыми, а с обычными временными цепочками, поскольку он планирует свою деятельность, ориентируясь на некоторый конечный временной отрезок. Кроме цепочки месяцев календарного года, которая используется часто, человек использует в практике и другие конечные цепочки месяцев. Так при планировании учебного процесса обычно используется цепочка месяцев учебного года (с сентября одного календарного года до мая следующего года). Некоторые учреждения составляют планы работы на полугодия, поквартально и проч., поэтому для решения разных практических задач иногда выделяются самые разные конечные цепочки из круговой цепочки месяцев. Таким образом, данная задача имеет не только учебную, но и практическую цель – научить ребят выделять разные конечные цепочки из круговой цепочки месяцев.

Задача 203. Эту задачу мы предлагаем детям для того, чтобы они освоились с календарем, и научились в нем быстро ориентироваться. Лексика в этой задаче почти не включает понятий нашего курса, все эти вопросы имеют практическую направленность (именно на такие вопросы детям чаще придется отвечать в жизни). Конечно, ответ на третий вопрос зависит от ответа на второй вопрос. Если в текущем феврале 28 дней, то в текущем года 365 дней. Если в текущем феврале 29 дней, то в текущем году 366 дней. Надеемся, в вашем классе не найдутся дети, которые начнут непосредственно пересчитывать дни в календаре или складывать число дней в месяцах. Хотя это тоже полезный опыт, продумайте сами, как работать с такими учащимися. Выражения типа «последняя среда марта» или «последнее воскресенье мая» тоже взяты из окружающей действительности. Например, на некоторых учреждениях можно увидеть надпись «Последнюю пятницу каждого месяца – санитарный день». Лучше если дети будут здесь работать с календарем, который они получили в процессе выполнения проекта «Мой календарь».

Задача 204. Необязательная. В отличие от задачи 203, здесь важно иметь представление о календаре, как о цепочке дней года. Соответственно к этой цепочке применима вся лексика, относящаяся к цепочкам, которая в этой задаче и закрепляется. Как видите, все эти утверждения не содержат информации о днях недели, они относятся только к порядку дней в году. Поэтому их значения не зависят от года (в отличие, например от задачи 203). Таким образом, при решении этой задачи дети могут использовать любой календарь, который есть под рукой, в том числе, конечно, и тот, который был выполнен в проекте «Мой календарь».

Задача 205. Необязательная. Ребятам уже приходилось решать аналогичные задачи про метро городов. Поэтому надеемся, вопросов эта задача не вызовет. Среди данных утверждений имеется одно, которое содержит информацию, истинность которой данная схема не позволяет проверить (пятое утверждение). Поэтому дети наверняка поставят против третьего утверждения значение «Н» (если конечно ваши дети не являются жителями Санкт-Петербурга). Среди остальных утверждений имеется лишь одно ложное, все остальные утверждения – истинны.

Задача 206. Первое утверждение задачи позволяет нам обозначить круг (точнее цепочку) слов из Словаря, среди которой есть смысл вести поиск. Это все слова от начала Словаря (слова АВАРИЯ) до слова ЙОТА. Однако  первой буквой искомого слова может быть только одна из слов из мешка Х, значит, для поиска нашего слова достаточно перебрать все слова на букву Д и на букву Е. Так мы находим слово ДЕСЯТЬ.

Задача 207. Необязательная. В процессе перебора всех слов с первой буквой  Щ, а второй Е, мы ищем два слова из четырех букв. Таких слов оказывается всего два и естественно одно из них идет раньше другого.

Ответ: в Словаре слово ЩЕКА идет раньше слова ЩЕЛЬ.

Задача 208. Это первая задача из новой серии. Детям она покажется, скорее всего,  совершенно естественной, как и многие практические информационные задачи, для решения которых не нужно обладать никакими специальными знаниями. Тем не менее, мы хотим обратить ваше внимание на важные стороны этой задачи. Во-первых, здесь используются понятия «вчера/сегодня», которые являются разговорными аналогами понятий нашего курса «предыдущий/следующий». Стоит обратить на это внимание ребят. Во-вторых, здесь впервые дети определяют истинность составных утверждений, типа «если – то». Это учит ребят видеть и анализировать причинно-следственные связи, а также учит ребят строить сложные рассуждения, что очень пригодится в старших классах (особенно на уроках геометрии). Наконец, некоторые утверждения в этой задаче касаются не двух (как мы привыкли в задачах на цепочки), а трех объектов «вчера – сегодня – завтра». Например, рассмотрим третье с конца утверждение. Здесь связь между «завтра» и «вчера» должна быть опосредована понятием «сегодня». Например, «Завтра будет воскресенье, значит сегодня суббота. Тогда вчера была пятница».

Задача 209. Знакомая ребятам задача на поиск одинаковых мешков, в которой дети могут использовать разные стратегии, например, перебор или деление мешков на группы по некоторым признакам.

Задача 210. Здесь на первый взгляд таблица похожа на двумерную таблицу для мешка, но, конечно, это не так. По сути, это несколько одномерных таблиц для мешков, соединенных в одну. В точки зрения целей и задач нашего курса, такой поворот совершенно естественен. Одна из задач нашего курса – научить детей работать с информацией, представленной различными способами, в том числе таблицей. Таблицы мы рассматриваем в основном на примере таблиц для мешка (одномерной и двумерной), но периодически мы предлагаем детям поработать и с другими таблицами, чтобы они учились осуществлять перенос знаний о таблицах на новое содержание. Последнее задание, как вы понимаете, мы даем для самопроверки.

Задача 211. Необязательная. В этой задаче дети строят классификацию чисел по количеству разрядов. При возникновении ошибок стоит: а) проверить, что каждое число каждого из мешков А, V и R соответствует описанию; б) соединить все числа из мешка W с числами из оставшихся мешков, чтобы убедиться, что все числа из мешка W попали в один из мешков и что они взяты ровно 1 раз.

Компьютерный урок «Круговая цепочка. Календарный порядок», 1 часть

Решение задач 211 – 218

Задача 211. В этой задаче ребятам самим нужно построить круговую цепочку – цепочку месяцев года. Для этого многие учащиеся вслух или про себя будут называть месяцы в их естественном (календарном) порядке и в таком же порядке выкладывать названия месяцев в окна цепочки. Названия месяцев в библиотеке идут в словарном порядке. Учащийся, который заметит это, поймет, что слово «ДЕКАБРЬ» стоит искать ближе к началу цепочки, а слово «ФЕВРАЛЬ» – ближе к концу. Дети, которые не обратят внимания на словарный порядок слов в библиотеке, чтобы найти каждое слово, будут просматривать библиотеку целиком.

Задача 212. Данная задача аналогична задаче 200 из учебника (см. комментарий к задаче 200).

Задача 213. Для решения этой задачи необходимо иметь представление о цикличности в смене времен года. В данном случае окон в цепочке больше, чем времен года. Поэтому нужно понимать, что в этой цепочке времена года будут встречаться не по одному раз. Так, исходя из практических представлений или с опорой на круговую цепочку времен года (приведенную в справке к этой задаче под знаком «?»), дети ставят после весны лето, затем осень, потом зиму. Но после этого в цепочке остаются пустые окна, значит, цепочку нужно продолжать – после зимы поставить весну, затем опять лето и так далее, пока в цепочке не закончатся окна.

Задача 214. К настоящему моменту дети наверняка неплохо ориентируются в календарных датах и могут расставить календарные даты одного года в цепочку (обычную). Так две календарные даты разных месяцев дети расставляют в цепочку по порядку следования месяцев одного года. Например, в одном календарном году 30 апреля идет раньше 1 мая. Если обе даты из одного месяца, то они расставляются в порядке возрастания чисел. Например, 28 декабря в календаре идет раньше 30 декабря. Если год не указан, то календарные даты образуют не обычную, а круговую цепочку, поскольку теперь у цепочки нет фиксированного начала и конца. Действительно, после 31 декабря одного года следует 1 января следующего года и цепочка замыкается.

Мы надеемся, что все перечисленные соображения знакомы ребятам из практической деятельности и уроков окружающего мира. Однако, если вы опасаетесь, что задача 214 без подготовки вызовет у детей трудности, после задачи 213 можно предложить ребятам выполнить проект «Мой календарь», где дети вспомнят особенности календарного порядка дат одного года, а уже после этого можно переходить к решению задачи 214 и других подобных задач.

В ходе решения данной задачи ребятам необходимо достроить круговую цепочку календарных дат, поэтому нужно принимать во внимание, как календарный порядок, так и цикличность календарных дат. В цепочке уже есть одна дата – 23 декабря. После нее могут стоять даты декабря (в которых числа больше 23), поэтому для начала будем искать среди дат именно их. Таких нет, значит, будем искать теперь даты января, поскольку после декабря в календарном порядке идет январь. Январских дат в наборе нет, как и февральских, а также мартовских. Значит следующая дата после 23 декабря в цепочке будет апрельская – 8 апреля. После нее ставим майскую дату и так перебираем месяцы по порядку, пока не доходим до последнего пустого окна и последней даты (27 ноября). В данном случае у нас нет ни одной пары дат из одного месяца, поэтому задачу можно решить, опираясь только на календарный порядок месяцев.

Задача 215. Для начала попробуем построить цепочку из частичных решений. Из второго утверждения мы получаем фрагмент цепочки «оранжевая треугольная – … – … – … – голубая круглая», из третьего утверждения – фрагмент «голубая круглая – … – … – … – синяя квадратная». Поскольку в цепочке ровно 6 бусин, в ходе проб и ошибок сразу становится ясно, что во втором и третьем утверждении не может идти речь об одной и той же голубой бусине, значит, в нашей цепочке имеется две голубых круглых бусины. Теперь попробуем состыковать два частичных решения между собой, принимая также во внимание и длину нашей цепочки. Оказывается это можно сделать двумя способами. Первый способ: «оранжевая треугольная – голубая круглая – … – … – голубая круглая – синяя квадратная». Второй способ: «голубая круглая – оранжевая треугольная – … – … – синяя квадратная – голубая круглая». После этого остаются два свободных места, на которые можно поставить две почти любые бусины (кроме оранжевой треугольной и синей квадратной).

Задача 216. Подобные задачи ребятам уже встречались (см. комментарий к компьютерной задаче 193 урока 28). Как сказано в условии, здесь получается три пары искомых слов: РОВНО и ВОРОН, ЛАЗЕР и РЕЗАЛ, ПОРКА и КАПОР.

Задача 217. Основное правило при решении этой задачи – не класть в один мешок два одинаковых мяча. Поэтому одна из стратегий заключается в том, чтобы брать по очереди группы одинаковых мячей, начиная с самых многочисленных и раскладывать мячи из этих групп в разные мешки. Например, у нас есть 4 одинаковых бело-серых мяча, положим их в 4 разных мешка. Аналогично поступим с группой красных мячей. Затем разложим мячи из групп по три одинаковых мяча и наконец, все оставшиеся мячи. При этом надо стремиться, чтобы мячи по мешкам распределялись примерно поровну, поэтому для разных троек мячей лучше выбирать разные тройки мешков. С некоторого момента придется принимать во внимание и число мячей в мешках, стремясь к тому, чтобы в каждом мешке оказалось ровно 6 мячей.

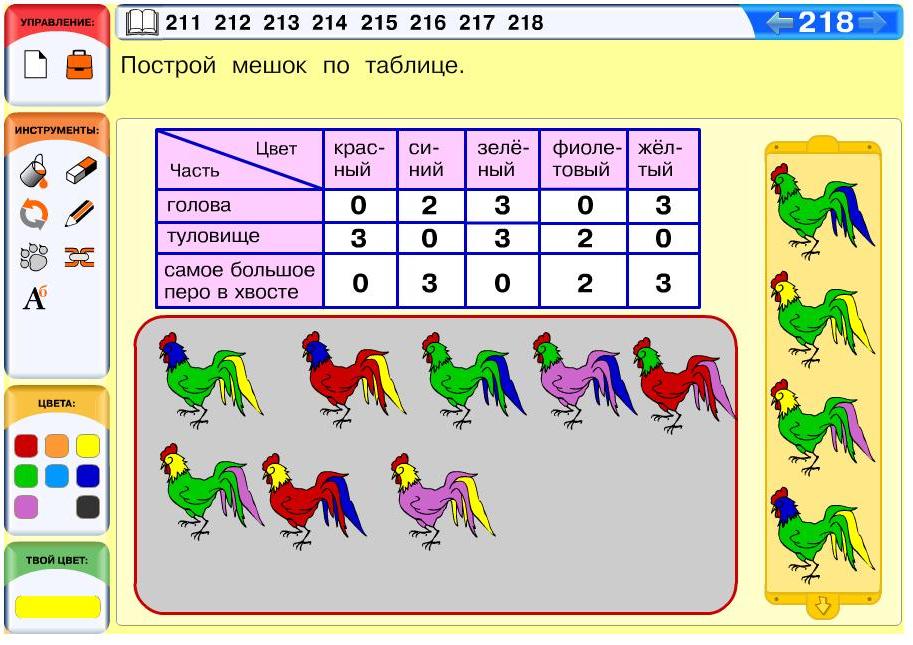
Задача 218. Необязательная. Обратите внимание, это сложная задача, пожалуй, одна из самых сложных в курсе 2 класса. Прежде чем читать дальше, попробуйте решить задачу самостоятельно. Вы, конечно, заметили, что задача с ходу не решается, хотя выглядит она достаточно стандартно, как задача на построение мешка по его двумерной таблице. Дело в том, что эта таблица только похожа на двумерную. По сути, она представляет собой трехмерную таблицу, ведь в таблице отражено 3 признака: цвет головы, цвет туловища и цвет самого большого пера в хвосте. При этом таблица составлена так, что отдельные признаки в ней не совмещены друг с другом, как у нас обычно происходит в двумерной таблице. Поэтому по ходу решения ребенок вынужден сам комбинировать признаки между собой и постоянно сверяться с таблицей. Таким образом, дети могут решать эту задачу только методом проб и ошибок.

По ходу решения можно сразу отбросить фигурки, которые в мешке лежать не могут, например, петухи с фиолетовыми головами или желтыми туловищами. После этого в библиотеке остаются 10 петухов, из которых мы в дальнейшем и будем выбирать. Начнем делать пробы наугад, ориентируясь пока только на верхнюю строку таблицы. Видно, что нам понадобятся разные комбинации признаков, поэтому пока постараемся не брать в мешок одинаковых фигурок. Итак, положим в мешок трех разных петухов с зеленой головой. Их можно сразу обвести или пометить галочками, все они нам понадобятся. Петухов с синей головой в библиотеке не два, а три. Пока можно положить три фигурки, но помнить, что потом одну из них придется убрать. То же самое с петухами с желтой головой, их пока можно положить 4. Теперь посчитаем число петухов в мешке с каждым цветом туловища и сравним полученные числа со второй строкой таблицы. Все петухи с красным туловищем нам понадобятся, их можно обвести. Получается, что нужно убрать из мешка одно петуха с зеленым туловищем и одного петуха с фиолетовым туловищем. Запомним это и посчитаем число петухов с разными цветами самого большого пера в хвосте, а затем сравним полученные числа с последней строкой таблицы. Петуха с фиолетовым пером нужно обвести. Из оставшихся не обведенными четырех петухов нужно убрать двух так, чтобы у них были разные цвета голов и разные цвета туловищ.

Компьютерный урок «Круговая цепочка. Календарный порядок», 2 часть

В отличие от предыдущего компьютерного урока, здесь детям предлагается сразу несколько задач на календарный порядок дат. Поэтому мы рекомендуем вам предлагать детям данный урок после выполнения проекта «Мой календарь».

Решение задач 219 – 224

Задача 219. Аналогичные задачи ребятам уже встречались (см. комментарий к компьютерной задаче 213). Для ее решения детям достаточно иметь представление о календарном порядке месяцев и цикличности их следования. Поэтому, после октября следует поставить ноябрь, затем декабрь, январь и т. д. , пока мы не дойдем до последнего пустого окна цепочки. Как и в компьютерной задаче 211 названия месяцев стоят в библиотеке в словарном порядке. Кто-то из детей догадается использовать это для более быстрого поиска слов, а кто-то для поиска каждого слова будет просматривать библиотеку полностью.

Задача 220. Здесь в каждое окно нужно вставить дату так, чтобы она шла в календарной цепочке позже предыдущей в нашей цепочке и раньше следующей. Вариантов в каждом случае, конечно, много. Так между 31 января и 20 марта можно поставить 1 февраля, 23 февраля, 8 марта и т.д. Вообще-то здесь можно вставить даже 29 февраля, поскольку мы не указываем, високосный или нет данный год. А вот 30 февраля, конечно, вставить нельзя, поскольку такой даты в календаре просто нет.

Задача 221. В целом эта задача аналогична компьютерной задаче 214 из предыдущего урока. Однако в отличие от задачи 214 здесь встречаются пары дат одного месяца, поэтому необходимо принимать во внимание, не только порядок месяцев, но и порядок следования дат в одном месяце. Видим, что среди месяцев нет февральских дат (а также даты 31 января), значит следующая после «30 января» дата в цепочке мартовская (17 марта). После нее идет дата «21 августа». Видим, что сентябрьских дат в наборе две, их нужно упорядочить по возрастанию чисел – сначала 11 сентября, а потом 30 сентября. Аналогично поступаем и дальше, пока не доходим до даты, предыдущей перед «30 января» – «31 декабря».

Задача 222. Аналогичная задача ребятам уже встречалась (см. комментарий к компьютерной задаче 205).

Задача 223. К настоящему моменту подобных задач ребята решали уже довольно много. Поэтому сильному учащемуся в случае ошибки достаточно указать на невыполнение одного из условий задачи, а слабому в случае затруднения – посоветовать собрать нужные бусины и строить цепочку из частичных решений.

Задача 224. Необязательная. В этой задаче ровно четыре решения. Из первого утверждения следует, что первая фигурка в цепочке – слон, а последняя – лось. Из второго утверждения следует, что вторая фигурка в цепочке – зебра, а предпоследняя – кенгуру. Что касается коровы, то она может быть как третьей в цепочке, так и четвертой. На оставшемся месте может стоять медведь, либо окапи.

Проект «Мой календарь»

В отличие от большинства проектов курса данный проект очень тесно связан с материалом учебника, а именно с уроками «Круговая цепочка. Календарный порядок». Поэтому лучше всего интегрировать его с изучением материла, посвященного круговым цепочкам. Это тем более удобно, что данный проект может занимать лишь часть урока. Так, можно на первом уроке по теме «Круговая цепочка. Календарный порядок» изучить лист определений, решить часть обязательных задач (не включающих работу с календарем). На втором уроке можно выполнить проект «Мой календарь» и решить оставшиеся обязательные задачи. Если у вас есть возможность отвести на данную тему 3 часа, то третий урок можно полностью посвятить решению задач.

Решение задач 20 – 24 из тетради проектов

Задача 20. Эта задача является в данном проекте основной. Ясно, что на нее уйдет достаточно много времени, но это вполне допустимо – остальные обязательные задачи не настолько важные, их можно задать на дом, решить на следующих уроках или вообще пропустить. Кроме того, мы сразу хотим вас предупредить, что время, которое потребуется на решение этой задачи, сильно будет зависеть от того, чем детям при решении можно будет пользоваться. Этот вопрос вы должны решить для себя заранее. Варианты могут быть, например, такие:

Вариант 1 (самый простой). Разрешить ребятам пользоваться готовым календарем аналогичного вида. Можно попросить детей принести в класс небольшие календарики или вывесить большой календарь на доске. Тогда задача детей будет заключаться только в том, чтобы найти на листе вырезания подходящие блоки для месяцев по образцу и наклеить эти блоки.

Вариант 2 (усложненный). Не давать детям готовых календарей, но заранее сообщить, каким днем недели в текущем году было 1 января (лучше записать это на доске). Тогда задача детей будет существенно сложнее, чем при первом варианте организации деятельности. Во-первых, нужно будет найти подходящий блок для января не по образцу, а по описанию. Во-вторых, для каждого следующего месяца детям придется самим выяснить, каким днем недели будет первое число, и найти подходящий блок (опять-таки по описанию). При таком варианте детям по ходу придется еще самим вспоминать, в каком месяце сколько дней (в частности, сколько дней в феврале текущего года). Если вы считаете это сложным, можно число дней в каждом месяце заранее выписать на доске.

Вариант 3 (самый сложный). Не давать детям готовых календарей и вообще каких-либо пояснений. Тогда большинству детей придется начать с текущего дня, ведь они наверняка знают, какое сегодня число и какой день недели (в крайнем случае, вы можете это напомнить в индивидуальном порядке). Далее ребенок сможет найти такой блок, в котором данное число приходится именно на этот день недели, и наклеить первым блок для текущего месяца. После этого придется считать, каким днем недели являются первые числа для следующих (и предыдущих месяцев). Как и в предыдущем варианте, вопрос о числе дней в месяцах детям придется решать самим по ходу дела.

Можно реализовать одновременно все три варианта в зависимости от силы детей – начать с третьего варианта, а для слабых детей в процессе выполнения проекта задание можно упрощать. Как видите, на листе вырезания на всех блоках по 31 дню. Поэтому лишние дни детям по ходу придется отрезать. Приведем пример рассуждений, которые ребенок может проводить в этой задаче. Допустим, вы выбрали 2 вариант работы с этой задачей. Ребенок знает, что в текущем году 1 января пришлось на среду. Теперь учащийся ищет на листе вырезания блок, в котором 1 число – среда. В январе 31 день, поэтому от соответствующего блока ничего отрезать не надо, можно его просто вырезать по границе и аккуратно в клеить в блок «Январь». Теперь посмотрим, на какой день недели придется 1 февраля. Если 31 января – пятница, значит, 1 февраля – суббота. Значит, теперь нам нужно найти блок, в котором 1 число – суббота. Вспоминаем, сколько дней в феврале текущего года, и отрезаем от соответствующего блока 2 или 3 последних дня. И так мы продолжаем работать, пока не заполним все блоки цепочки в задаче.

Задачи 21 и 22. Эти задачи по сравнению с задачей 20 – менее серьезные и более простые. Здесь надо лишь раскрасить некоторые даты (заранее известные). Собственно, здесь мы делаем наш календарь более похожим на обычные календари, ведь в них, как правило, отмечены праздничные дни. Заодно дети начинают потихоньку учиться ориентироваться в цепочке, построенной в задаче 20. Мы советуем выбирать в этой задаче не слишком едкий красный цвет, такой, чтобы даже на раскрашенных клетках было видно число. Содержательно эта задача совсем несложная и при дефиците времени можно оставить ее на дом.

Задача 23. Как и задачи 21 и 22, эта задача, скорее, общеразвивающая, чем учебная. Именно в этой задаче учащийся делает безличный календарь личным, то есть превращает его в такой, который он сможет назвать «мой календарь» (до настоящего момента это был просто календарь). Для этого ребенок отмечает в календаре собственные праздники, то есть дни, которые ребенок считает для себя особыми. Здесь нет и не может быть никаких критериев правильности выбора таких дней, они целиком и полностью зависят только от ребенка. Это могут быть личные праздники: день рождения, именины, день первой победы на соревнованиях и проч. Это могут быть дни рождения друзей, знакомых и даже домашних животных. Ну и конечно, это могут быть семейные праздники – дни рождения или именины родственников, день свадьбы родителей и проч. Необязательно, чтобы дат было ровно столько, сколько строк в таблице, но если ребенок затрудняется, стоит ему помочь, чтобы он записал хотя бы 2-3 даты. Если ребенок хочет отметить дат больше, чем 5, попросите записать их названия на отдельном листе и вклеить в тетрадь проектов.

Задача 24. Необязательная. Здесь ребятам необходимо построить круговую цепочку календарных дат, поэтому нужно принимать во внимание как календарный порядок, так и цикличность календарных дат. Выберем любую дату, например 29 ноября. После нее могут стоять даты декабря (или 30 ноября), поэтому для начала будем искать среди дат именно их. Таких дат нет, значит, будем искать теперь даты января, поскольку после декабря в календарном порядке идет январь. У нас есть одна подходящая дата – 31 января, значит, ее и надо поставить в цепочку после 29 ноября. Дальше будем искать февральские даты (таких в наборе нет), затем мартовские даты (таких нет). Получаем, что следующая дата в цепочке после 31 января – 8 апреля. Так будем двигаться и дальше, пока даты в наборе не закончатся. У нас есть лишь две даты, приходящиеся на один месяц, – 12 июня и 30 июня. Их расставляем в цепочку по возрастанию чисел. Во всех остальных случаях для построения цепочки достаточно знакомства с круговой цепочкой месяцев.